0.   引言

随着信息技术的不断发展，电力系统逐渐发展成为电力信息物理融合系统(cyber-physical power system，CPPS)^[1-3]，其不再具有传统电力系统封闭性的特点，极易遭受网络攻击。2011年2月，伊朗不什尔核电站受到名为“震网”(Stuxne)的病毒攻击，剥夺了核电设备的控制权，通过恶意操作使得大量核电站离心机停用。2015年12月，因恶意网络攻击导致乌克兰国家电网遭受重大损失^[4]。现有网络攻击策略从对电网结构影响可分为以破坏电力网络拓扑结构为目的的攻击^[5-9]和不以破坏电力网络拓扑结构为目的的攻击，后者主要包括虚假数据注入攻击(false data injection attacks，FDIAs)^[10-13]、负荷的重分配^[14-15]，拒绝服务攻击^[16]等。FDIAs是2009年Yao Liu等人^[10]提出的一种新型电力网络攻击，具有较强的隐蔽性，攻击者利用传统状态估计对不良数据检测的漏洞，能够成功地向CPPS注入FDIAs，影响电力系统的状态估计^{[5, 10, 17]}。因此，如何实现FDIAs的检测与辨识已成为保障CPPS安全运行的一个新挑战。

近年来，国内外针对FDIAs进行了大量研究，文献[18]提出了基于无迹卡尔曼滤波(unscented Kalman filter，UKF)和加权最小二乘相结合的状态估计算法来实时检测虚假数据攻击。文献[19]针对FDIAs将改进的噪声估计器与UKF动态估计相结合建立安全预测状态估计模型。文献[20]提出了一种伪量测模型与自适应无迹卡尔曼滤波(adaptive unscented Kalman filter，AUKF)相结合的状态估计方法，并基于估计值偏差进行虚假数据的辨识。上述检测方法均基于动态估计与静态估计值间的偏差量或者欧氏距离等指标来检测攻击，但当UKF更新过程中存在虚假数据时，FDIAs检测误警率增大。文献[21]提出了一种基于历史数据库的短期状态预测检测方法。文献[22]利用可信的历史数据提出了基于马尔科夫链理论和欧氏距离相结合的攻击检测方法。文献[23]提出一种基于双向门控循环单元和自注意力的攻击检测方法。文献[24]提出了一种基于最大信息系数-双层置信极端梯度提升树的电网虚假数据注入攻击定位检测方法。文献[25]提出了基于长短时记忆网络和生成对抗网络的VRB储能系统虚假数据注入攻击检测方法。文献[26]提出一种低成本对抗性隐蔽虚假数据注入攻击方案及对应的检测方法。文献[27]提出了一种基于极端梯度提升结合无迹卡尔曼滤波的电网虚假数据注入攻击的检测方法。上述检测方法通过深入挖掘历史数据信息对状态量进行预测实现攻击检测，此类方法需要大量的历史数据，优点是不受量测量中虚假数据的影响。但随着新能源的大量接入使得电力系统波动性增加，使用历史数据进行预测的方法难以应对系统中的波动问题，预测状态量精确度降低，导致FDIAs检测率降低。

针对上述问题，本文针对FDIAs的检测进行研究，首先使用肯德尔相关系数对日期类型进行量化取值，再使用加权灰色关联分析进行相似日的选取，在此基础上建立基于最小二乘支持向量机的日前负荷预测模型。然后将预测负荷通过潮流计算求解的节点状态量与UKF动态状态估计得到的状态量进行加权混合预测。最后，求解出状态量混合预测值和静态估计值间的偏差变量，基于偏差变量提出攻击检测指数(attack detection index，ADI)，根据ADI的分布进行FDIAs检测。若检测到量测数据中存在FDIAs，则用混合预测状态量对该时刻的量测状态量进行修正。

1.   虚假数据注入攻击模型

将实际交流电网视为非线性状态估计系统，向电网中注入FDIA，则攻击后的量测量为

式中：${z_i}$为无攻击状态下第$i$个测量向量；$z_i^{{\text{bad}}}$为第$i$个受攻击后的测量向量；$i$为系统节点数；$n$为受攻击的节点集；${a_i}$为攻击向量$a$的第$i$个攻击量；根据电力系统状态估计可知系统受到攻击前后的状态量分别为$\hat x$、${\hat x^{{\text{bad}}}}$，其攻击前后产生的偏差向量为$c$，则受到攻击后状态量为${\hat x^{{\text{bad}}}} = \hat x + c$。由于系统不良检测机制是根据系统量测数据残差来确定检测阈值$\dot \tau$，则攻击前后的量测残差分别为${\delta _1}$和${\delta _2}$。

式中：$z$为测量向量；$h( \cdot )$为系统的非线性量测函数。当攻击向量$a$满足$a = h(\hat x + c) - h(\hat x)$时，攻击前后的量测残差满足${\delta _2} \leqslant {\delta _1}$，则注入的虚假数据可成功避开不良数据检测机制。

2.   基于UKF的电力系统动态状态估计

电力系统动态估计的数学模型主要由动态方程和量测方程组成^[28]，其表达式为

式中：${x_{k + 1}}$和${x_k}$分别为$k + 1$和$k$时刻的状态量，包含电压幅值、电压相角；${z_{k + 1}}$为$k + 1$时刻的量测量；${q_k}$为$k$时刻的系统噪声；${r_{k + 1}}$为$k + 1$时刻的量测噪声；$f( \cdot )$为非线性的状态转移函数。

UKF通过引入无迹变换对状态转移函数$f( \cdot )$进行近似^[28]，其基本原理是根据状态量均值点构造方差为状态量方差的Sigma点集，再对Sigma点集中的各个点进行非线性变换，通过加权求和获得非线性变换后的状态量和方差。在本文中使用UKF动态状态估计对电力系统所采集到的量测数据进行迭代计算，根据选取的状态转移函数以及系统状态量的变化趋势实现对系统中各个节点状态量的预测估计，得到系统下一时刻各节点的电压幅值和相角值。基于UKF的动态估计的主要步骤主要包括预测和更新两部分。

1）预测。

${P_k}$为$k$时刻状态量的协方差，根据所选取的采样策略构造Sigma点集$\{ {\chi _{i, k}}\}$，通过无迹变换得到状态量和方差的下一步预测值。

式中：$k + 1|k$表示利用$k$时刻的量测量来预测$k + 1$时刻的状态量；${Q_k}$为$k$时刻的系统噪声协方差阵；$L$为Sigma点集个数；$w_i^c$和$w_i^m$分别为采样策略决定的均值和方差的权值。

2）更新。

根据状态预测中的${x_{k + {\text{1|}}k}}$, ${P_{k + {\text{1|}}k}}$构造Sigma点集$\{ {\chi _{i, k}}\}$，实现对量测值进行预测：

式中：${y_{i, k + 1}}$为$k + 1$时刻第$i$个量测量的预测值；${\bar y_{k + 1}}$为$k + 1$时刻预测值的均值；${S_{k + 1}}$为$k + 1$时刻预测值的协方差矩阵；${r_k}$为$k$时刻的量测噪声量；${R_{k + 1}}$为$k + 1$时刻量测噪声量${r_{k + 1}}$的方差矩阵，在本文中，${r_{k + 1}}$的均值为0，标准差为0.02^[28]；${C_{k + 1}}$为$k + 1$时刻状态量与量测量间的相关性协方差矩阵；${K_{k + 1}}$为卡尔曼增益；${\bar x_{k + 1}}$为状态量的滤波值；${P_{k + 1}}$为状态量的协方差矩阵。在本文中，UKF状态估计使用的状态转移函数$f( \cdot )$为两参数指数平滑法。

从式(13)中可知，在预测更新过程中，UKF更新过程会受到量测数据${z_{k + 1}}$中的虚假数据影响，当${z_{k + 1}}$中存在虚假数据时，会导致状态量滤波值${\bar x_{k + 1}}$精度降低，检测误报率增加。

3.   基于相似日的最小二乘支持向量机日前负荷预测模型

在实际电力网络中，日负荷曲线会受多个因素影响，其中占主导的是气象因素^[29-30]和日期类型^[31]。因此，本文选取历史日负荷数据集时引入了影响该地区负荷变化的主要气象因素，包括平均温度、最高温度、最低温度、相对湿度、日期类型和日期距离因子^[32-33]。通过对影响因子进行加权灰色关联分析，求出历史日与待预测日的相似度，选取相似度较大的历史日作为训练集。

在文献[29, 32]中将日期类型划分为工作日、双休日，其由于忽略了日期类型间的时间过渡关系，使得日期类型的量化取值不够精确，无法真正反映日期类型与负荷间的关系。因此，本文首先将历史日负荷数据按日期类型分为7类，然后将各日期类型负荷数据均值作为7个典型的日期类型负荷数据，再通过计算典型日期类型负荷间的肯德尔相关系数(Kendall's tau-b)来量化日期类型的取值。

设$S = \{ ({x_i}, {y_i})\} _{i = 1}^n$为$n$对独立同分布的数据序列，$n$为数据序列中数据的个数。当集合$S$中任两个元素$({x_i}, {y_i})$与$({x_j}, {y_j})$满足${x_i} > {x_i}$且${y_i} > {y_j}$或${x_i} < {x_i}$且${y_i} < {y_j}$，则两个元素为同序对；反之，为逆序对；当${x_i} = {x_i}$或${y_i} = {y_j}$时，则既不为同序也不为逆序。则肯德尔相关系数$\tau$的计算公式为

式中：$c$为$S$中的同序对元素对数；$d$为$S$中的逆序对元素对数；${a_i}$、${b_i}$分别为序列$x$、$y$中第$i$个相同元素组成的集合中所包含的元素个数。日期类型的量化取值结果如表 1所示。

表  1  日期类型的量化取值

Table  1.  Quantization value of the date type

类型	周一	周二	周三	周四	周五	周六	周日
周一	1	0.953	0.957	0.947	0.919	0.936	0.767
周二	0.953	1	0.977	0.976	0.961	0.952	0.785
周三	0.957	0.977	1	0.983	0.961	0.966	0.789
周四	0.947	0.976	0.983	1	0.969	0.962	0.796
周五	0.919	0.961	0.961	0.969	1	0.955	0.809
周六	0.936	0.952	0.996	0.962	0.955	1	0.816
周日	0.767	0.785	0.789	0.796	0.809	0.816	1

下载: 导出CSV 

| 显示表格

由表 1可知，周一到周日的7种日类型与对应的日负荷曲线的关联特性存在较大差异，如周日的日负荷与周一至周六的日负荷相关性较弱，而周一至周六的日负荷彼此相关性较强。因此，通过对日期类型对应的日负荷进行相关性分析，得出日负荷与日期类型间的变化关联特性，实现对日期类型的量化取值，进一步在对负荷预测时准确的引入影响负荷变化的日期影响因子，能够避免人为取值的主观性，使得日期类型特征取值更加具有科学性。

选取各影响因子构建历史日的特征向量序列：

式中：${{\boldsymbol{X}}_i}$为第$i$个历史日的主要影响因子序列；${x_{im}}$为第$i$个历史日的各类影响因子；${{\boldsymbol{X}}_0}$为待预测日的主要影响因子序列；$i = 1, 2, \cdots , n$，$n$为历史日天数；$k = 1, 2, \cdots , m$，$m$为影响因子个数。对历史日数据序列进行均值化无量纲处理得：

待预测日特征向量与各个历史日特征向量中对应影响因子的差值为

待预测日特征向量与各个历史日特征向量中对应影响因子的关联系数为

式中：$\mathop {\min }\limits_i \mathop {\min }\limits_k \Delta {x_{ik}}$为预测日与历史日对应的第$k$个影响因子的差值最小值；$\mathop {\max }\limits_i \mathop {\max }\limits_k \Delta {x_{ik}}$为对应的第$k$个影响因子的差值最大值；$\rho$为分辨系数，$\rho \in (0, 1)$，$\rho$值越小，其分辨率越高。在本文中$\rho$取值为0.5。从而得到灰色关联系数矩阵：

式中：${\omega _{{\text{nm}}}}$为历史日n的第m个影响因子的关联系数。将式(25)系数矩阵中各行向量相加即可得到影响因子与负荷间的加权关联度：

引入日期距离量化因子${a^t}$，采用文献[34]进行取值，$a = 0.95$；$T$为历史日与预测日相距的天数。则有：

将所得的关联度进行排序，选取关联度大于0.9以上的15个历史日作为待预测日的相似日。

3.1   最小二乘支持向量机模型

LSSVM是将支持向量机(support vector machines，SVM)中的二次规划问题转化为线性规划问题，使得计算的复杂性大幅度降低，求解速度得以增强。假设数据样本集表示为

式中：${x_i}$为第$i$个输入向量；${y_i}$为第$i$个输出向量；$i \in [1, N]$, $N$为训练样本数；$n$为输入样本维数。将样本集$Z$通过非线性映射$\phi (x)$到高维特征空间，再进行线性回归，其回归函数表达式为

式中：$\omega$为权值向量；$\phi (x)$为核函数，表征低维空间到高维空间的映射关系；$b$为偏置因子。

为使LSSVM结构风险最小化，其优化求解的目标函数与约束条件为

式中：$\eta$为惩罚系数；${e_i}$为第$i$个松弛变量。利用拉格朗日乘子${\lambda _i}$对式(30)进行求解，则：

根据KKT条件，对其求解有：

通过将式中的$\omega$、$e$消除后获得预测函数为

式中：$K( \cdot )$为径向基核函数，$K({x_i}, {x_j}) = {e^\mu }$，$\mu = - ||{x_i} - {x_j}|{|^2}/2{\sigma ^2}$；$\sigma$为核函数宽度，表征低维空间到高维空间的映射关系。

4.   自适应加权混合预测

针对本文第2节中所提到的基于UKF状态估计进行虚假数据检测时存在的弊端，本文采用自适应加权混合预测方法，将UKF与第3节所建立的基于LSSVM的日前负荷预测模型结合，以应对虚假数据对UKF的影响，将两种预测模型的预测结果进行加权求和，依据预测结果偏差对权值进行实时修正，具体方法为

假设$k$时刻，基于UKF动态估计得到$k + 1$时刻的状态量为$\hat x_{k + 1}^U$，基于LSSVM日前负荷预测得到的负荷结果经潮流计算得到的$k + 1$时刻的状态量为$\hat x_{k + 1}^l$，将两种模型预测得到的状态量进行自适应加权求和得到的混合预测状态量为

式中：${w_{k + 1}}$为自适应混合权值，由于两种方法在不同时刻的状态量预测值的准确度不同，为使得混合后预测效果最佳，则需根据$k$时刻的预测偏差对$k + 1$时刻的${w_{k + 1}}$进行修正。当基于UKF预测精度更高时给予较高权重，否则给予后者较高权重，表达式如式(35)—(36)所示：

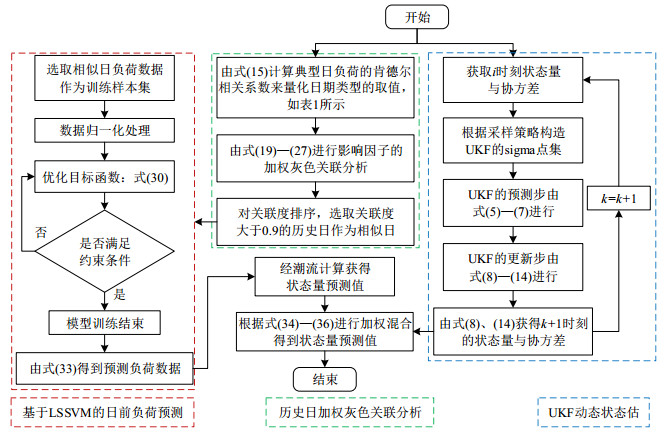
式中：${c_{k + 1}}$为$k + 1$时刻的遗忘因子，并且${c_{k + 1}} \in [0, 1]$，其取值越大表明对前一时刻的权重保留越小；当系统中$k$时刻量测量${z_k}$满足$||{z_k} - h({\hat x_k})|| < \dot \tau$时，则${z_k}$不存在虚假数据。利用式(37)计算$k + 1$时刻的遗忘因子，当$k$时刻状态量值预测误差越小，在$k + 1$时刻多保留$k$时刻的权重，即在$k + 1$时刻${c_{k + 1}}$取值越小；反之成立。当$k$时刻存在虚假数据并成功的被检测出时，表明当前时刻的混合预测精度较高，保留当前时刻的预测权重值，即在$k + 1$时刻${c_{k + 1}}$取值为0。${x_k}$为剔除虚假数据后存入历史库的状态量；${z_k}$为$k$时刻系统的量测状态量；$\dot \tau$的取值根据$\gamma$分布表可知，在本文中，$m$为量测值的个数，且$m = 41$；$n$为状态量的个数，且$n = 27$；$m - n$为冗余度；当显著性水平为0.95时，$\dot \tau = 23.685$，自适应加权混合预测流程如图 1所示。

图  1  自适应混合预测流程

Figure  1.  Adaptive hybrid prediction process

下载: 全尺寸图片 幻灯片

本文所提的日前负荷预测模型的精确度取决于历史相似日的选取以及LSSVM模型参数的选取。但由于系统状态多变，所提的LSSVM日前负荷预测模型的预测值与实际会存在一定的偏差，导致预测状态量存在偏差；UKF状态估计的精度取决于状态转移函数的选取以及系统状态量的变化趋势。在本文中LSSVM日前负荷预测与UKF动态估计进行状态量预测时相互独立，保证了两者的预测精度互不影响，通过引入自适应权重值将两种预测值进行加权求和，使得混合预测值结合了UKF实时在线估计的优势和基于LSSVM的日前负荷预测模型可充分挖掘历史数据信息且不受虚假数据攻击影响的优势，通过预测偏差量进行权重值的实时修正，将各自模型的优劣进行互补，实现更高精度的状态值预测，进而更有效应对FDIAs。

5.   FDIA的攻击检测和修正

为了检测虚假数据攻击，本文根据混合预测值和静态估计值间的偏差向量提出了一种攻击检测指数(attack detection index，ADI)，其表达式如下：

式中：${\hat x_{i + 1}}$为$i + 1$时刻的静态状态估计值；${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} _{i + 1}}$为$i + 1$时刻的状态混合预测值；${x'_{i + 1}}$为$i + 1$时刻预测值与静态估计值的偏差；${x'_{}}$为$i = 1$到$i + 1$时刻的偏差向量；$\bar x'$为${x'_{}}$的平均值；${cov} (.)$为协方差函数；$\tilde \tau$为检测边界阈值。

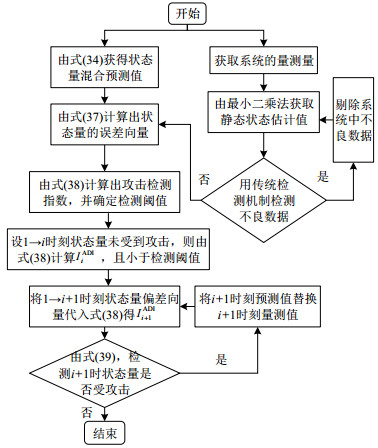
根据无攻击情况下的状态预测与静态状态估计值间的偏差向量经式(38)计算出正常情况下的攻击检测指数序列$\kappa$，再根据序列$\kappa$中各个变量的分布范围确定检测阈值$\tilde \tau$，本文中，$\tilde \tau = \max (\kappa )$。假设前$i$时刻状态量不存在虚假数据攻击，然后加入$i + 1$时刻的预测值计算$i + 1$时刻状态量的攻击检测指数$I_{i + 1}^{{\text{ADI}}}$，将$I_{i + 1}^{{\text{ADI}}}$与$\tilde \tau$作比较；若$I_{i + 1}^{{\text{ADI}}} \leqslant \tilde \tau$，则$i + 1$时刻量测量不存在虚假数据攻击；否则$i + 1$时刻量测量存在虚假数据攻击，则将$i + 1$时刻预测值${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} _{i + 1}}$替换静态估计值${\hat x_{i + 1}}$，然后继续下一时刻状态量的攻击检测，流程如图 2所示。

图  2  FDIAs的检测与修正流程

Figure  2.  FDIAs detection and correction process

下载: 全尺寸图片 幻灯片

6.   仿真分析

本文通过选用IEEE-14和IEEE-39节点测试系统进行仿真分析。加权灰色关联的相似日选取部分、最小二乘向量机预测、UKF动态状态估计以及攻击检测部分使用Matlab R2019a实现，处理器为Intel(R) Core(TM)i7-7700HQ CPU@2.80GHz，RAM8.0GB；仿真数据选用云南某地区8月1日至9月27日负荷，数据采集每15min一次，一天共96次负荷数据和96次气象数据。参照文献[35]将负荷数据分为14、39两个区域并分别接入到IEEE-14、IEEE-39节点系统中。

选取9月27日作为攻击检测日，首先通过加权灰色关联分析选取相似日，然后通过LSSVM对9月27日负荷进行预测，根据负荷预测求出状态量，将求出的状态量与UKF的估计值进行加权求和，再利用混合预测值与静态估计值间的偏差量求出攻击检测指数ADI，并根据ADI的分布进行FDIAs的检测与辨识。

6.1   日前负荷预测仿真分析

以预测9月27日节点9的负荷为例，按照本文第3节的方法对日类型进行特征量化，对历史气象数据、日期距离以及预测日的气象数据进行数据预处理，构建影响日负荷曲线的影响因子母序列及子序列，再通过加权灰色关联分析法对影响因素进行关联相似度计算，选出相似度大于0.9的15个历史日作为相似日，结果如表 2所示。

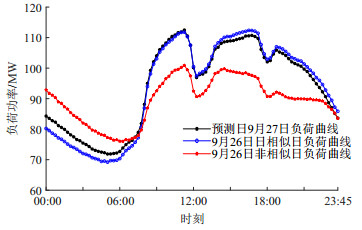
表  2  关联分析选出的相似日

Table  2.  Similar days selected by correlation analysis

日期	相似度		日期	相似度
8月2日	0.907		9月18日	0.901
8月15日	0.902		9月20日	0.902
8月23日	0.903		9月21日	0.911
8月28日	0.901		9月22日	0.902
8月30日	0.902		9月24日	0.901
9月1日	0.907		9月25日	0.931
9月13日	0.901		9月26日	0.942
9月17日	0.910

下载: 导出CSV 

| 显示表格

将相似日、非相似日与预测日的日负荷曲线进行对比，如图 3所示。由图可知，使用加权灰色关联选取出的相似日与预测日的日负荷特性更为接近。因此将相似日作为预测日的训练集，能够大幅度降低数据内存、提高模型训练效率与预测精度。

图  3  不同日负荷曲线对比

Figure  3.  Comparison of different daily load curves

下载: 全尺寸图片 幻灯片

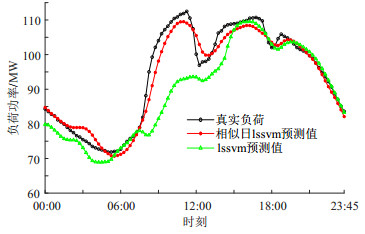
将选取出的15组历史日负荷数据以及对应的气象数据和9月27日的气象预测数据作为LSSVM模型的输入量，对9月27日的负荷进行预测。此外，从8月1日到9月26日的历史负荷数据中随机选取15天数据导入LSSVM模型中作为预测对照实验。在本文中，LSSVM模型的参数gam取值为10，sig2取值为1000，训练集为15。相似日样本数据与随机日样本数据经LSSVM预测模型得到的负荷预测结果如图 4所示。

图  4  预测负荷曲线对比

Figure  4.  Comparison of predicted load curve

下载: 全尺寸图片 幻灯片

为验证本文方法与随机历史日下LSSVM模型的负荷预测准确率，使用平均绝对百分比误差(mean absolute percentage error，MAPE)作为量化指标，其计算公式为

式中：$n$为负荷的量测次数，$n = 96$；${P'_i}$为预测负荷；${P_i}$为预测日的真实负荷。

各方法的MAPE计算结果如表 3所示。

表  3  各类方法MAPE对比

Table  3.  MAPE comparison of various methods

方法	MAPE/%
本文方法	2.06
随机日下的LSSVM方法	5.32

下载: 导出CSV 

| 显示表格

由表 3可知，本文所提方法的MAPE值为2.06%，相较于随机日下的LSSVM模型的MAPE值降低了3.26%，本文所提出的方法能够有效提升负荷预测的精度。

6.2   自适应加权混合状态预测仿真分析

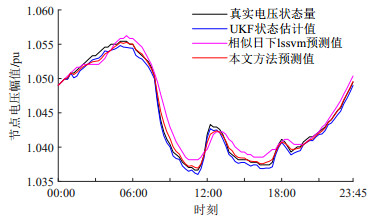
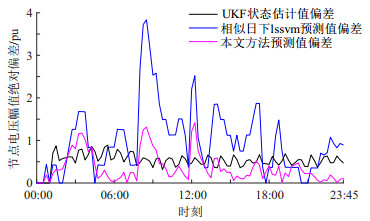
场景1：首先将本文方法的预测负荷代入IEEE-14节点系统中求出节点9的状态量。设当前系统未受到FDIA的攻击，即攻击强度为零，将通过潮流计算出的状态量作为系统的真实状态量。为使得量测信息更加的接近实际情况，在真实状态量中加入均值为0，方差为1%的高斯白噪声作为系统的量测量。根据本文第4节的自适应加权混合预测方法求出状态量的预测值${\hat x_{k + 1}}$，各方法下的状态量预测结果对比如图 5、图 6所示。

图  5  电压幅值状态预测对比

Figure  5.  Voltage amplitude state prediction comparison

下载: 全尺寸图片 幻灯片

图  6  电压幅值绝对偏差对比

Figure  6.  Voltage amplitude absolute deviation comparison

下载: 全尺寸图片 幻灯片

由图 5和图 6可知，本文方法对状态量预测效果最好，通过相似日选取出的历史日与待预测日的负荷特征高度相似，降低了非相似日负荷对训练集数据的影响，提升了日前负荷预测模型的准确性，使得预测的状态量准确度更高；最后使用自适应加权将日前负荷预测模型所得状态值与UHF状态估计值进行加权求和，将两种预测模型的优缺点进行互补融合，进一步提高了状态预测的精度。

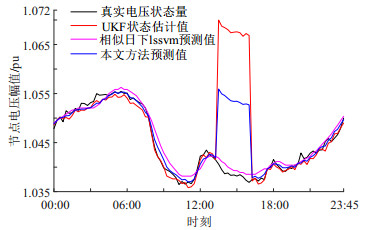
场景2：在场景1中的第55~65次量测数据中注入攻击强度为电压幅值量3%的攻击量，其攻击量采用文献[10]的攻击模型进行构造。其各方法所得的状态量预测结果如图 7所示。

图  7  连续注入强度为3%的攻击后预测值对比

Figure  7.  Comparison of predicted value after attack with continuous injection intensity of 3%

下载: 全尺寸图片 幻灯片

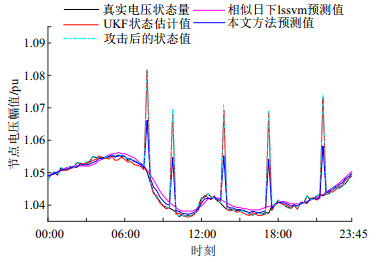
场景3：在9月27日的96个量测数据中随机注入5个攻击强度为电压幅值量3%的攻击量，随机注入攻击后的电压幅值预测值比较如图 8所示。

图  8  攻击强度为3%的电压幅值预测比较

Figure  8.  Comparison of voltage amplitude prediction with attack strength of 3%

下载: 全尺寸图片 幻灯片

由图 7和图 8可知，当节点9处的量测数据中发生虚假数据注入攻击时，相似日下LSSVM模型的状态预测效果最好，由于UKF动态估计容易受量测数据中虚假数据的影响，导致在状态预测时效果最差，本文方法的效果介于两者之间；由图 6可知，在无虚假数据注入时，相似日下LSSVM模型的状态预测效果比UKF动态估计的效果差，使得相似日下LSSVM模型的状态预测值不易满足误报率的要求。因此本文方法将UKF动态估计与LSSVM日前负荷预测模型相结合，可在有虚假数据注入攻击的情况下相比单一方法提高了检测率，在不发生虚假数据注入攻击时降低检测的误报率。

6.3   FDIA的检测仿真效果对比分析

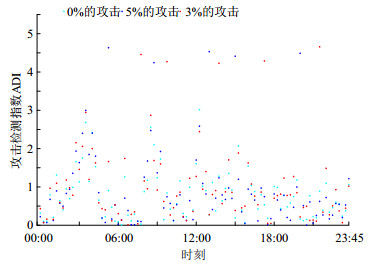
按照场景3的攻击方式，向节点9的96个量测量中随机注入3组攻击强度为电压幅值量0%、3%和5%的5个攻击向量，并对其进行残差检验，以验证所注入的攻击量能否躲避传统检测机制的检测，其在不同时刻受攻击后残差结果如表 4所示。

表  4  不同攻击时刻的残差结果

Table  4.  Residual results at different attack times

攻击时刻k	32	40	56	70	87
3%攻击量	19.732	17.637	14.286	19.256	20.478
攻击时刻k	22	36	53	61	81
5%攻击量	21.839	18.989	21.411	23.649	21.131

下载: 导出CSV 

| 显示表格

由表 4可知，注入攻击强度为3%和5%的攻击量后，经残差计算在不同攻击时刻其残差结果均小于第4节中所求出的传统检测阈值$\dot \tau = 23.685$，说明本文所注入的攻击量能够躲避传统检测机制，具有隐蔽性。进一步，根据式(37)—(39)计算出各种攻击强度下的攻击检测指数ADI。不同攻击强度下ADI分布如图 9所示。

图  9  不同攻击强度下的ADI分布

Figure  9.  ADI distribution under different attack intensity

下载: 全尺寸图片 幻灯片

由图 9可知，在发生攻击的情况下，由于攻击量注入，致使攻击检测指数远大于正常情况下的攻击检测指数。因此，本文根据攻击强度为0%时的ADI分布确定攻击检测阈值为3.14，不仅能够准确的识别出量测数据中是否存在虚假数据攻击，而且能够降低波动性的影响。但随着攻击强度的降低，所提出的攻击检测指数ADI与正常时的ADI会趋于同一分布，导致依据正常状态下的ADI确定检测边界阈值会使得误报率增加，导致检测难度加大。

为了验证本文所提方法检测的性能，将本文所提方法与基于短期状态预测的FDIAs检测方法^[11]、基于支持向量机(support vector machine，SVM)的FDIA检测方法^[12]、基于UKF动态状态估计的FDIA检测方法^[18]进行对比。分别向IEEE-14和IEEE-39节点系统中随机注入20次攻击强度为电压幅值量3%~5%的攻击量，其攻击量采用文献[10]的攻击模型进行构造。检测效果采用检测率${P_{{\text{A}}0}}$、误报率${P_{{\text{A1}}}}$两个指标进行量化，表达式为

式中：${C_{{\text{TP}}}}$为成功检测出攻击的次数；${C_{{\text{TN}}}}$为成功检测出正常的次数；${C_{{\text{FP}}}}$为检测为异常的正常数据次数；${C_{{\text{FN}}}}$为检测为正常的异常数据次数；不同系统下的检测结果比较如表 5、6所示。

表  5  IEEE-14节点下系统检测结果比较

Table  5.  Comparison of detection results in IEEE-14 bus system

方法	检测率/%	误报率/%
本文检测方法	95.83	4.17
基于UKF检测方法	89.58	10.42
基于SVM检测方法	87.50	12.50
本文LSSVM日前预测检测方法	92.71	7.29
基于短期状态预测检测方法	91.67	8.33

下载: 导出CSV 

| 显示表格

表  6  IEEE-39节点系统下检测结果比较

Table  6.  Comparison of detection results in IEEE-39 bus system

方法	检测率/%	误报率/%
本文检测方法	93.75	6.25
基于UKF检测方法	90.63	9.37
基于SVM检测方法	86.46	13.54
本文LSSVM日前预测检测方法	91.66	8.34
基于短期状态预测检测方法	90.63	9.37

下载: 导出CSV 

| 显示表格

由表 5、6可知，本文检测方法在IEEE-14、IEEE-39节点系统中检测率分别达到95.83%、93.75%，并且本文方法的检测率比其他基于单一方法的检测率均有不同程度的提高，说明本文所提方法能够有效应对FDIAs。

7.   结论

针对CPPS中存在的虚假数据注入攻击，本文在使用肯德尔相关系数对日期类型进行量化的基础上，引入加权灰色关联分析进行相似日的选取，建立基于LSSVM的日前负荷预测模型，通过潮流计算节点状态量；再利用UKF动态估计进行系统状态量预测，通过自适应加权混合将两种方法所得状态量进行求和，并根据混合预测值与静态估计值间的偏差向量提出了攻击检测指数ADI。然后基于ADI的分布来检测FDIAs。若系统遭受FDIAs，则使用该时刻的混合预测状态量替换该时刻的量测状态量。最后在IEEE-14和IEEE-39节点系统中进行仿真，可得到如下结论：

通过使用肯德尔相关系数进行日期类型的量化特征值计算，避免了人为取值的主观性，引入加权灰色关联分析选取出与待预测日高度相似的历史日作为相似日，提高了负荷预测的精确性并降低数据迭代时间。

通过将UKF动态估计与基于LSSVM的日前预测模型进行自适应混合，能够有效克服UKF受虚假数据的影响以及LSSVM预测模型受系统负荷突变的影响，根据预测误差进行自适应权重的不断修正，提高了状态量预测精度。

根据预测值与静态估计值间偏差向量提出了一种攻击检测指数ADI，并根据ADI的分布进行FDIAs的攻击检测，能够有效的应对FDIAs。