Mid- and High- Frequency Oscillation Suppression Strategy for MMC-HVDC System Based on DC Current Feedback
-
摘要: 基于模块化多电平换流器的柔性直流输电(modular multilevel convertor based high voltage direct current,MMC-HVDC)系统存在的中高频振荡问题严重危胁电力系统的正常运行。首先,基于MMC的动态相量模型,建立了MMC的交流侧阻抗模型;其次,利用阻抗法分析控制环节及控制参数对MMC阻抗特性的影响,得到了功率外环、电流内环及控制链路延时是导致MMC呈现负阻尼特性的主要原因;再次,在分析现有基于电压前馈环节和电流内环的协同振荡抑制策略不足的基础上,提出了功率外环附加直流电流反馈的振荡抑制策略,极大程度消除系统中的谐波分量,改善了MMC的阻抗特性;最后,通过电磁仿真软件验证理论分析和抑制措施的正确性与有效性。Abstract: The serious mid-and high- frequency oscillation issue in modular multilevel convertor based high voltage direct current (MMC-HVDC) systems poses a significant threat to the normal operation of power systems. In this paper, we firstly established an AC-side impedance model of the MMC based on its dynamic phase vector model. Secondly, we analyzed the impact of control loops and control parameters on MMC impedance characteristics using the impedance method, and identified the power outer loop, current inner loop and control loop delay as the main factors causing MMC to present negative damping characteristics. And then, based on an analysis of the limitations of existing oscillation suppression strategies that are based on voltage feedforward loops and current inner loops, we proposed an oscillation suppression strategy that adds DC current feedback to the power outer loop, which can greatly eliminate harmonic components in the system and improve MMC impedance characteristics. Finally, the correctness and effectiveness of the theoretical analysis and proposed suppression measures were verified through electromagnetic simulation software.
-
0. 引言
模块化多电平换流器(modular multilevel converter,MMC)具有模块化程度高、输出谐波特性好、扩展性强的特点[1],成为柔性直流输电(modular multilevel convertor based high voltage direct current,MMC-HVDC)工程中的主流拓扑结构。随着MMC-HVDC工程的不断发展,发生了多起中高频振荡事件:2017鲁西直流工程发生了
1270 Hz左右的振荡现象;2018年渝鄂直流工程在调试过程中发生了700 Hz和1800 kHz左右的振荡现象[2-4]。后续在对振荡现象的研究中发现:MMC的底端控制环节及控制链路延时对MMC的中高频段阻抗特性影响较大[5-7]。由于控制系统及控制链路延时作用于MMC,导致其呈现出的阻抗特性易与互联的弱阻尼系统发生交互作用,使得系统发生振荡频率范围较大的宽频振荡现象,柔直系统中的中高频振荡会使系统的电压和电流发生畸变,对电网的电能质量造成不利影响;若振荡发生后不能及时消除,还可能引起系统的故障保护误动作,使得换流站闭锁跳闸,导致系统功率失衡[8-9]。明晰控制环节及控制链路延时对MMC的稳定性影响机理,设计振荡抑制策略,提升系统的稳定性,避免振荡事件发生,成为大规模MMC应用需要解决的热点和难点问题之一。研究MMC对柔性直流输电系统的影响,首先要建立能准确反映MMC运行特性的模型。文献[10]基于动态相量法建立了MMC的动态相量模型。文献[11]将时域下的动态相量模型转化到频域,建立了MMC的dq轴交流侧阻抗模型。MMC动态相量模型能在保证较高精度的基础上降低模型阶数,减少仿真时间[12]。阻抗分析法通过稳定分析判据以及Bode图能直观得到系统的振荡风险区,简化稳定性分析过程,被广泛用于分析MMC-HVDC系统稳定性[13-15]。
对于存在振荡风险的系统,考虑到经济性和可实施性,目前主要采用有源抑制措施来提升系统的稳定性[16]。文献[17]通过优化控制器参数抑制了振荡现象,但是这种方法对系统规模有一定要求。文献[18]提出了在电压前馈环节附加滤波器的振荡抑制措施。文献[19]提出了在电流内环附加带阻滤波器的振荡抑制措施。文献[20]考虑了正负序控制器对系统的影响,提出在多个控制环节附加级联陷波滤波器的多频段振荡抑制措施。
但上述文献对振荡的抑制主要是在电压前馈环节和电流内环附加不同的滤波器来优化MMC的阻抗特性,对通过附加阻尼与改善功率外环控制结构协同解决振荡问题的研究较少。
针对目前存在的问题,本文建立了考虑锁相环、内外环控制、环流抑制控制以及延时环节的完整MMC小信号模型。通过拉普拉斯变换及矩阵运算,建立了MMC的交流侧阻抗模型,分析了各个控制环节及控制参数对MMC阻抗的影响规律。在电压前馈环节和电流内环的协同振荡抑制策略的基础上,提出了功率外环附加直流电流反馈的振荡抑制策略。在PSCAD/EMTDC电磁暂态仿真软件中建立相应的仿真模型,验证了系统建模、理论分析及振荡抑制策略的正确性。
1. MMC的数学模型
1.1 MMC的动态相量模型
MMC的单相电路拓扑结构如图1所示(以A相为例)。图1中:Rarm和Larm分别为表征MMC损耗的桥臂等效电阻和桥臂电抗;RS和LS分别为交流系统的等效内电阻和电感;RT和LT分别为联结变压器的等效电阻和电感;kT是变压器变比;us是交流系统电压;uv是MMC交流侧与联结变压器阀侧电压;up是公共耦合点(point of common coupling,PCC)处的电压;Udc和Idc分别为直流电压和直流电流;i是MMC交流侧电流;ip和in分别为上、下桥臂电流;icir是桥臂环流;mP和mN分别为上、下桥臂的调制信号;
uMCP 和uMCN 别为上、下桥臂子模块总电容电压;uCP和uCN分别为上、下桥臂投入的子模块电容电压之和;O点为直流侧中性点。将每个桥臂等效成一个平均子模块,得到MMC的桥臂平均模型,等效后的桥臂电容Carm为
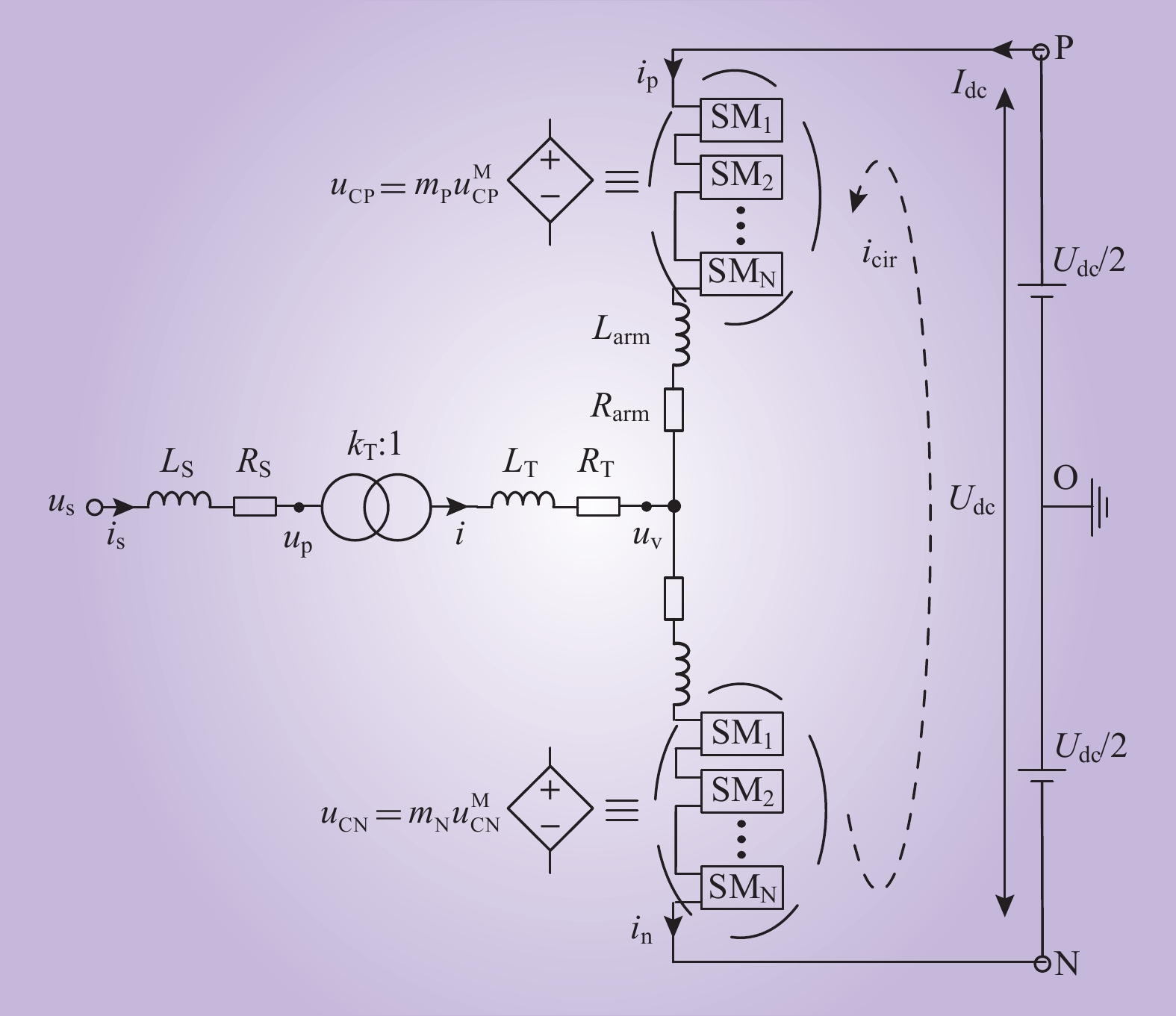
Carm=CSM/CSMNN (1) 式中:CSM为每个子模块SM的电容;N为每个桥臂所含子模块数。
由于MMC独特的拓扑结构及内部动态,运行过程中的电压和电流等电气量均包含多个频率分量。在建立MMC模型时,非基频次谐波对系统的影响不能忽略。动态相量法作为一种基于反映元件动态特性的状态变量所对应的时变傅里叶系数而推导的建模方法,通过保留对应变量的傅里叶系数中较大的系数项,使得模型能包含所有需要考虑的谐波,在实现模型简化的基础上,保留系统的主要特征,确保建模的准确度。
基于动态相量法得到建立在dq轴下的MMC的10阶动态相量模型[21]。该模型为MMC的电气部分模型,与MMC的控制系统、交流系统等联立可得到完整的MMC-HVDC系统闭环模型。
1.2 MMC控制系统的dq轴模型
MMC的控制系统由锁相环、功率外环、电流内环和环流抑制控制器组成。
1)电气坐标系与控制坐标系的关系。
MMC的动态相量模型建立在与电网电压矢量Us同步的dq旋转坐标系下;而MMC的控制系统建立在定位于锁相环测量得到的PCC点电压up的dcqc同步旋转坐标系下(控制坐标系下的变量用xc表示)。MMC电气部分和控制部分所处的坐标系通过PCC处的电压up的相位θ相连,通过坐标变换矩阵可以实现电气量与控制量之间的转换。2种坐标系关系如图2所示。
2)傅里叶系数符号与坐标变换矩阵的关系。
根据动态相量法,MMC的电气量可以表示为各次频率下傅里叶系数的叠加,即变量x(t)为
x(t)=x0+n∑k=1xdkcos(kωt)−n∑k=1xqksin(kωt) (2) 式中:下标“0”是变量的直流分量;下标“dk、qk”是变量在以k倍频旋转的dq同步旋转坐标系下的d、q轴分量。
本文的动态相量模型是基于式(2)的形式建立的,对应的同步旋转坐标系的q轴超前于d轴。为了保持动态相量模型与电磁暂态模型的一致性,电磁暂态模型中采取的Park变换需要与动态相量中傅里叶系数的符号相对应。采用如式(2)的形式建立动态相量模型时,基频下的矢量在2个坐标系下的关系为
{xd=xcdcosθ−xcqsinθxq=xcdsinθ+xcqcosθ{xcd=xdcosθ+xqsinθxcq=xqcosθ−xdsinθ (3) 由于控制系统中二倍频分量的相序为负,在进行坐标变换时的角度应该是–2θ,对应的坐标变换公式为
{xd2=xcd2cos2θ+xcq2sin2θxq2=xcq2cos2θ−xcd2sin2θ{xcd2=xd2cos2θ−xq2sin2θxcq2=xd2sin2θ+xq2cos2θ (4) 当采用d轴超前于q轴的坐标轴系进行建模时,式(3)中的θ 需要变为–θ,二倍频分量的坐标变换矩阵中θ 的符号同样需要改变。
3)锁相环控制。
通过锁相环得到电压up的相位,为坐标变换提供相位参考。锁相环动态方程为
{dxPLLdt=kiPLLucpqdθdt=ucpq+xPLL+ω0 (5) 式中:kpPLL和kiPLL分别为锁相环PI环节的比例和积分参数;ω0为电网角频率;θ 为锁相环输出的相位。
4)功率外环及电流内环控制。
MMC的外环控制采用定功率控制,为电流内环控制提供电流参考。控制坐标系下流入PCC点的有功功率P和无功功率Q分别为
{P=icducpd+icqucpqQ=icducpq−icqucpd (6) 功率外环动态方程为
{dxPdt=kipq(Pref−P) ; icdref=kppq(Pref−P)+xPdxQdt=kipq(Q−Qref) ; icqref=kppq(Q−Qref)+xQ (7) 式中:Pref、Qref分别为有功和无功功率的参考值;kppq和kipq分别为外环PI环节的比例和积分参数;
icdref 和icqref 分别为内环d、q轴电流的参考值。通过电流内环控制得到MMC基频调制信号在控制坐标系下的d、q轴分量
Mcd 和Mcq 。电流内环的动态方程为{dxiddt=kii(icdref−icd)Mcd=ucpd+ωLsumicq−kpi(icdref−icd)−xidUdc (8) {dxiqdt=kii(icqref−icq)Mcq=ucpq−ωLsumicd−kpi(icqref−icq)−xiqUdc (9) 式中:kpi和kii分别为内环PI环节的比例和积分参数。
5)环流抑制控制。
通过环流抑制控制器得到MMC倍频调制信号在控制坐标系下的d、q轴分量
Mcd2 和Mcq2 。环流抑制控制动态方程为{dxcird2dt=kii2(icird2ref−iccird2)Mcd2=2ωLarmiccirq2+kpi2(icird2ref−iccird2)+xcird2Udc (10) {dxcirq2dt=kii2(icirq2ref−iccirq2)Mcq2=−2ωLarmiccird2+kpi2(icirq2ref−iccirq2)+xcirq2Udc (11) 式中:kpi2和kii2分别为环流抑制控制器PI环节的比例和积分参数。
6)控制系统延时。
MMC-HVDC控制系统中的延时主要包括测量、滤波、控制处理等环节引入的延时。MMC控制链路延时为数百微秒,本文采用五阶Pade近似对控制延时进行拟合。以基频调制信号的d轴分量Md为例,Md经延时环节处理的动态方程为
{ddtMdT=PT1MdT+PT2Mdz ; Md=PT3MdT+PT4MdzMdT=[MdT1MdT2MdT3MdT4MdT5]TPT1=[01000001000001000001−30\;240T5−15120T4−3360T3−420T2−30T]PT2=[0 0 0 0 1]TPT3=[60480T−5 0 6720T−3 0 60T−1] ; PT4=[−1] (12) 式中:Mdz为控制系统输出的调制信号,经延时环节处理后得到Md;MdTi为由Pade近似引入的状态变量;T为延时时间。
将MMC的电气部分模型及控制系统模型联立,可得完整的闭环MMC系统的非线性状态空间模型,即为MMC的大信号模型,通过该模型能够计算出系统的稳态运行点,该模型是建立MMC小信号模型的基础。
1.3 小信号模型
使用小扰动法将上文建立的非线性状态空间模型在稳态运行点处线性化。下文中粗体书写的变量表示包含多个dq轴分量的列向量,上标“c”表示该变量为控制坐标系下的量
{uMCP=[uMCP0uMCPduMCPquMCPd2uMCPq2]Ti=[idiq]T,icir2=[icird2icirq2]Tup=[updupq]T,M1=[MdMq]TMz=[MdzMqz]T,M2=[Md2Mq2]T (13) MMC电气部分的小信号模型为
ddt[ΔuMCPΔiΔicir0Δicir2]=[KuKuiKuic0Kuic2KiuKi02×102×2Kic0u01×2Kic001×2Kic2u02×202×1Kic2][ΔuMCPΔiΔicir0Δicir2]+[KuMKiMKic0MKic2M]ΔM1 + [KuM2KiM2Kic0M2Kic2M2]ΔM2+[05×2Kiup01×202×2]Δup+[05×102×1Kic0udc02×1]ΔUdc (14) 坐标变换方程的小信号模型为
{Δx=Ks1Δxc+Ks2Ks3ΔθΔxc=Kc1Δx+Kc2Kc3Δθ (15) {Δx2=Ks21Δxc2+Ks22Ks23ΔθΔxc2=Kc21Δx2+Kc22Kc23Δθ (16) 锁相环的小信号模型为
Δ˙XPLL=Kθ1ΔXPLL+Kθ2Δucp (17) 功率外环的小信号模型为
{˙ΔXPQ=Kx1ΔPQref+Kx2KG1Δic+Kx2KG2ΔucpΔicref=KPQ1ΔPQref+KPQ2KG1Δic+KPQ2KG2Δucp+KPQ3ΔXPQ (18) 电流内环的小信号模型为
{Δ˙Xi=Kxi1Δicref+Kxi2ΔicΔMc1=KM1Δicref+KM2Δic+KM3ΔXi+KM4Δucp+KM5ΔUdc (19) 环流抑制控制的小信号模型为
{Δ˙Xicir2=Kxi211Δiccir2ΔMc2=KM21Δiccir2+KM22ΔXicir2+KM23ΔUdc (20) 表征控制链路延时的Pade近似小信号模型为
{Δ˙MdT=PT1ΔMdT+PT2ΔMdzΔMd=PT3ΔMdT+PT4ΔMdz (21) {Δ˙MqT=PT1ΔMqT+PT2ΔMqzΔMq=PT3ΔMqT+PT4ΔMqz (22) 将式(14)~(22)联立,即可得到MMC的完整小信号模型,该模型是对MMC进行阻抗建模及小信号稳定性分析的基础。
2. MMC的阻抗模型及稳定性分析
2.1 MMC的阻抗模型
本文对MMC交流侧的阻抗特性进行分析,认为直流电压的小扰动量ΔUdc=0,通过拉普拉斯变换将时域下的MMC小信号模型转到频域,经过矩阵运算可得到MMC的交流侧阻抗模型。
通过拉普拉斯变换,将式(14)转到频域,得到MMC电气部分的频域模型为
[Ku−sIKuiKuic0Kuic2KuMKuM2KiuKi−sI02×102×2KiMKiM2Kic0u01×2Kic0−sI01×2Kic0MKic0M2Kic2u02×202×1Kic2−sIKic2MKic2M2]⋅[uMCPiicir0icir2M1M2] +[05×2Kiup01×202×202×202×2]up=[014×1] (23) 坐标变换方程的频域模型为
{ucp=Kc1up+Kc2Kuc3θic=Kc1i+Kc2Kic3θMc1=Kc1Mz+Kc2KMc3θ (24) {iccir2=Kc21icir2+Kc22Kic23θMc2=Kc21M2+Kc22KMc23θ (25) 结合式(24)(25),可得锁相环的频域模型为
θ=(kpPLL+kiPLL/s)s+(kpPLL+kiPLL/s)ucpds[−sinθscosθs]up (26) 式中:
ucpds 和θs分别为ucpd 和θ 的稳态值。功率外环的频域模型为
icref=KPQKG1ic+KPQKG2ucp (27) 电流内环的频域模型为
Mc1=Ks1icref+Ks2ic+Ks3ucp (28) 环流抑制控制的频域模型为
Mc2=Kssiccir2 (29) 控制链路延时的频域模型为
Gdel=e−sT≈n=5∑k=0(2n−k)!n!k!(n−k)!(−sT)kn=5∑k=0(2n−k)!n!k!(n−k)!(sT)k (30) 整理式(23)~(30),得到MMC的闭环频域模型为
[Ku−sIKuiKuic0Kuic2KuMKuM2KiuKi−sI02×102×2KiMKiM2Kic0u01×2Kic0−sI01×2Kic0MKic0M2Kic2u02×202×1Kic2−sIKic2MKic2M202×5Km102×102×2Km202×202×502×202×1Kmm102×202×2]GA⋅[uMCPiicir0icir2M1M2]XMMC =[05×2−Kiup01×202×2Km3Kmm2]GBup (31) 通过矩阵运算得到的矩阵为
KMMC=G−1AGB (32) 矩阵KMMC的第6行和第7行为交流电流i与交流侧电压up之间变换矩阵,即为MMC的交流侧导纳矩阵,对导纳矩阵求逆即可得到MMC的交流侧阻抗矩阵,可以表示为
ZdqMMC = [Zdd(s)Zdq(s)Zqd(s)Zqq(s)] (33) 根据文献[22]可得MMC的正序阻抗模型为
ZMMC = 2(ZddZqq−ZdqZqd)Zdd+Zqq+j(Zdq−Zqd) (34) 2.2 基于阻抗模型的MMC稳定性分析
基于建立的MMC阻抗模型,分析不同控制环节对MMC阻抗特性的影响。系统参数设置如表1所示。
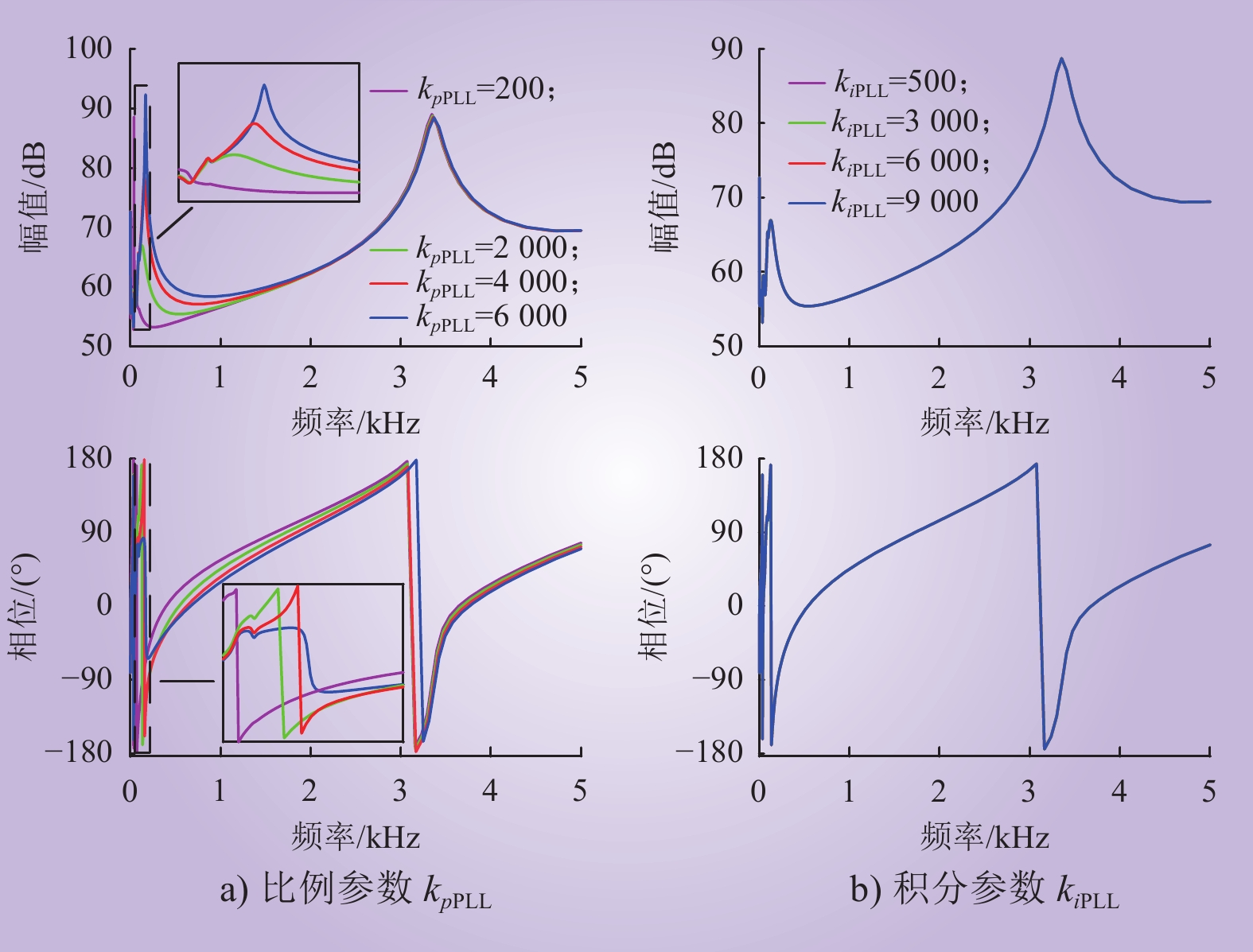
表 1 系统主要参数Table 1. Main parameters参数 数值 系统参数 网侧交流电压/kV 525 额定直流电压/kV 840 额定功率/(MV·A) 1250 变压器 变压器变比/kV 525/437 变压器短路比/% 14 MMC 桥臂子模块数/个 500 桥臂等效电阻/Ω 0.5 桥臂等效电感/mH 140 桥臂子模块电容/μF 11000 控制器参数 锁相环PI参数(kpPLL、kiPLL) 2000 、3000 功率外环PI参数(kppq、kipq) 0.3、10 电流内环PI参数(kpi、kii) 0.4、16.7 环流抑制PI参数(kpi2、kii2) 0.4、40 Pade近似延时时间/μs 300 2.2.1 锁相环对MMC阻抗的影响
分别改变锁相环控制参数kpPLL和kiPLL,不同锁相环控制参数下MMC的阻抗特性如图3所示。由图3可知:锁相环控制参数只会对MMC较低频段的阻抗特性产生一定影响。
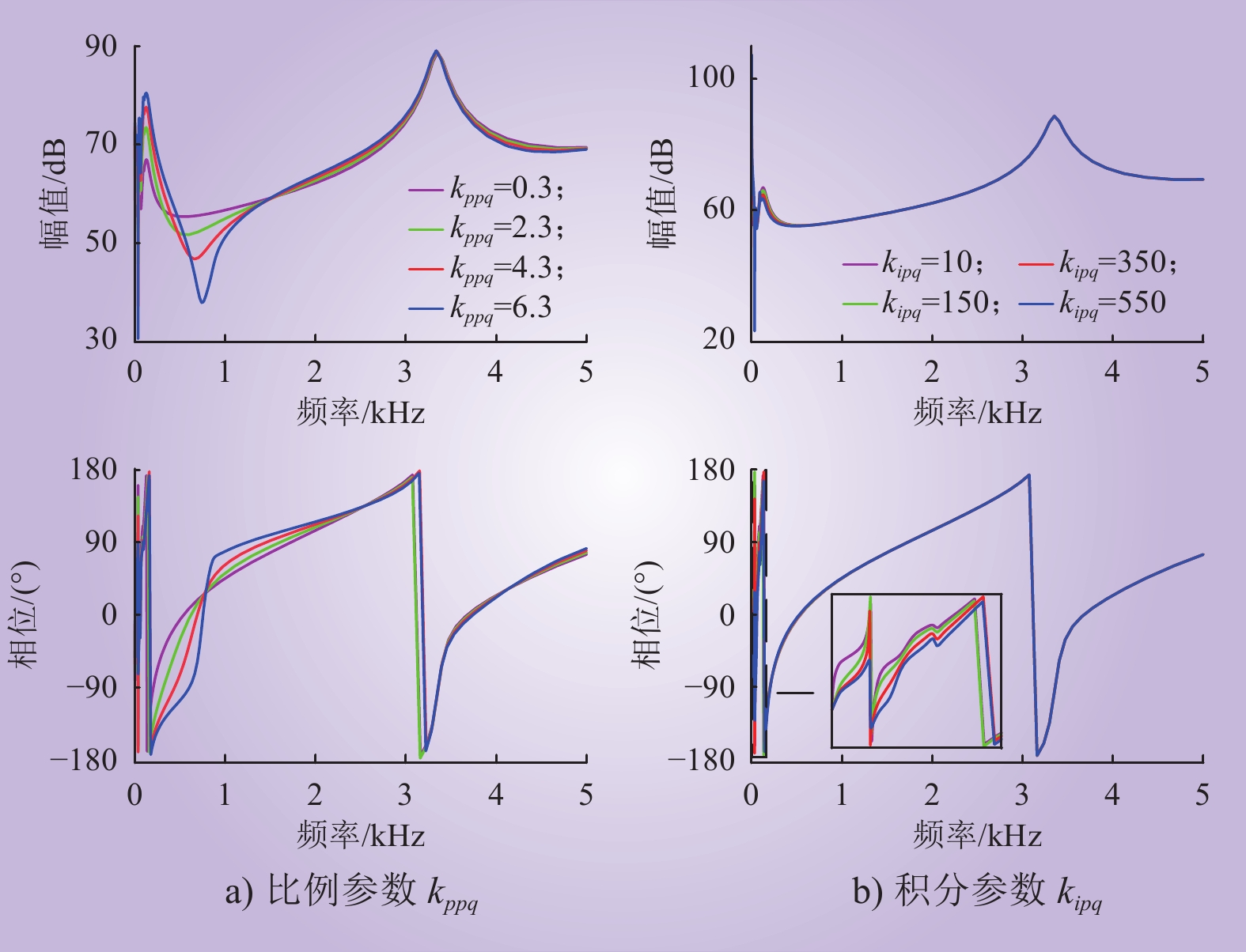
2.2.2 外环控制对MMC阻抗的影响
分别改变功率外环控制参数kppq和kipq,不同外环控制参数下MMC的阻抗特性如图4所示。由图4可知:外环控制参数中的比例参数kppq对MMC中高频段的阻抗特性影响较大。
2.2.3 内环控制对MMC阻抗的影响
分别改变内环控制参数kpi和kii,不同内环控制参数下MMC的阻抗特性如图5所示。根据图5可知:内环控制参数中的比例参数kpi对MMC中高频段的阻抗特性影响较大。
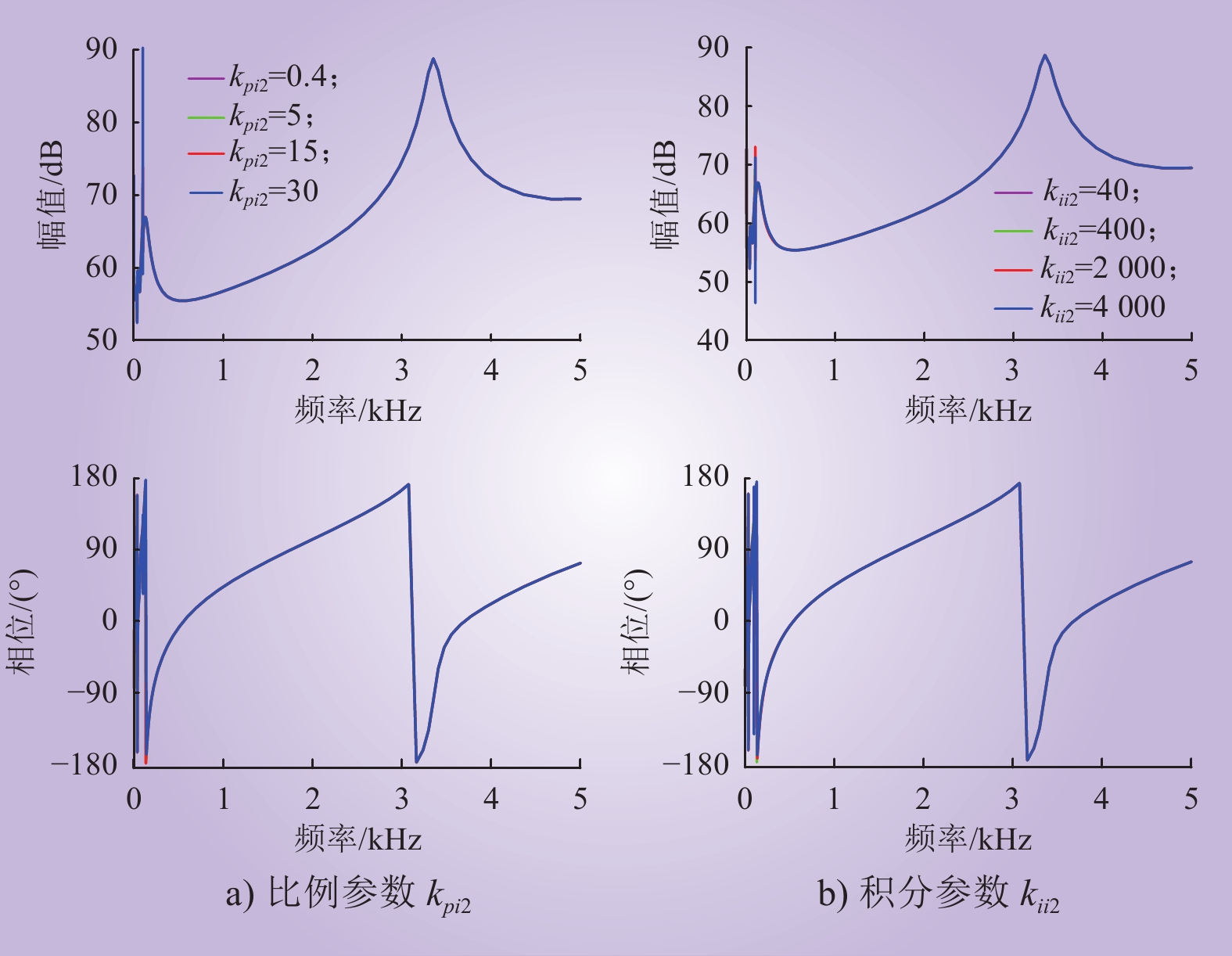
2.2.4 环流抑制控制对MMC阻抗的影响
分别改变环流抑制控制参数kpi2和kii2,不同环流抑制控制参数下MMC的阻抗特性如图6所示。由图6可知:环流抑制控制参数对MMC阻抗特性几乎没有影响。
2.2.5 控制链路延时对MMC阻抗的影响
改变控制链路延时T,不同控制链路延时下MMC的阻抗特性如图7所示。由图7可知:控制链路延时对MMC阻抗特性的影响很大,随着延时时间的增大,MMC的阻抗幅值出现峰值的频段降低,阻抗呈现负阻尼的频段也会向低频段转移。即控制链路延时越大,系统的振荡风险频段越低。
2.2.6 控制系统对MMC阻抗的影响分析
综上所述,MMC阻抗特性受锁相环和环流抑制控制的影响较小,在进行中高频振荡分析时可以忽略其对MMC阻抗特性的影响。功率外环及电流内环主要影响MMC中高频段的阻抗特性,比例系数增大会导致MMC阻抗幅值出现较大的波动,并且会增大MMC阻抗的负阻尼频段,使其更容易与交流系统阻抗产生振荡现象,在对分析MMC中高频段阻抗特性时不可忽略。延时环节是影响MMC阻抗特性的主要因素,控制链路延时的增大会导致系统的振荡风险频段向低频段转移,其作为导致MMC阻抗出现负阻尼特性的主要因素,在对MMC建模及分析时不可忽略。
3. MMC-HVDC系统的中高频振荡抑制策略
3.1 基于电压前馈环节的振荡抑制策略
在考虑控制链路延时时,MMC的阻抗会呈现多频段的负阻尼特性,为了避免MMC与互联的交流系统产生振荡现象,需要重塑MMC的阻抗特性。在电压前馈环节附加滤波器可以消除电网前馈电压中的谐振分量,有效改善MMC的负阻尼特性,实现MMC-HVDC系统振荡抑制。
电压前馈环节附加低通滤波器可以改善MMC的负阻尼特性,但是会造成振荡频段的转移,并且附加单一的低通滤波器,无法消除MMC阻抗存在的多个负阻尼频段。通过在电压前馈环节附加级联带阻滤波器,可以有效改善系统存在的多个振荡风险频段。
针对本文中MMC阻抗存在的2个负阻尼频段,在电压前馈环节附加由2个带阻滤波器级联组成的级联带阻滤波器,滤波器的传递函数为
KBSF(s)=s2+ω2c1s2+ξ1ωc1s+ω2c1s2+ω2c2s2+ξ2ωc2s+ω2c2 (35) 式中:ξ为阻尼系数;ωc=2πfc,fc为带阻滤波器中心频率,fc=(fup+fdown)/2,fup和fdown分别为根据MMC的负阻尼频段设计的滤波器上、下截止频率。
在本文中,带阻滤波器的截止频段设置为[140, 540]Hz及[
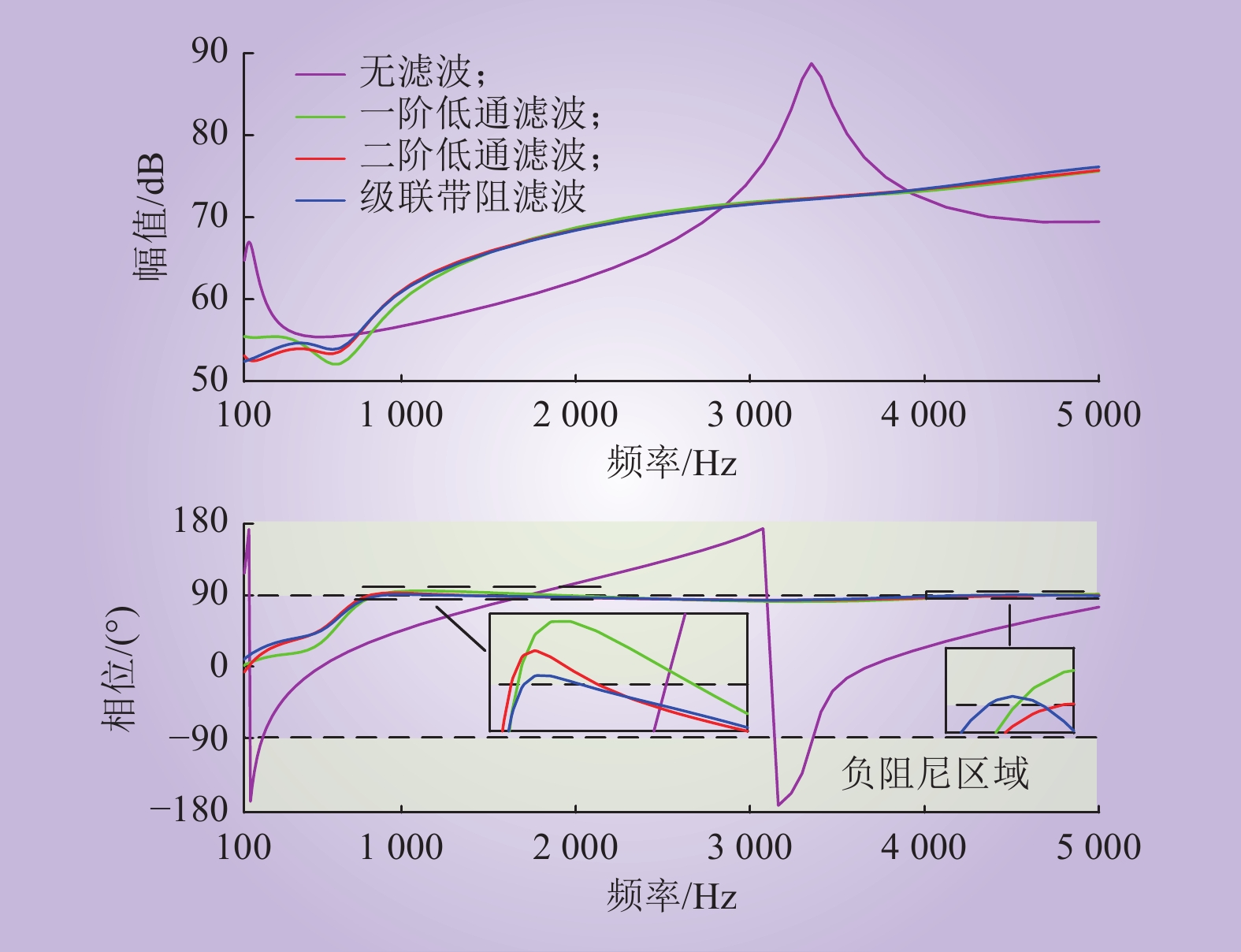
1400 ,3600 ]Hz。在电压前馈环节分别附加截止频率为100 Hz的一阶、二阶低通滤波器以及级联带阻滤波器,MMC的阻抗特性如图8所示。
由图8可以看出:电压前馈环节附加低通滤波器后,MMC原有的阻抗特性得到改善,但是会向其他频段引入负阻尼特性。通过在电压前馈环节附加级联带阻滤波器,可更好改善系统的负阻尼特性,MMC阻抗的负阻尼频段相较于附加低通滤波器时大大减小,但是仍然无法完全消除MMC的负阻尼频段,系统仍然存在一定的振荡风险,还需要进一步优化MMC的阻抗特性。
3.2 基于电压前馈环节和电流内环的协同振荡抑制策略
在电压前馈环节附加滤波器后,MMC的中频段阻抗仍然会呈现负阻尼特性,MMC-HVDC系统仍然存在谐振风险。采用基于电压前馈环节和电流内环的协同振荡抑制策略(下文称为“策略一”)该抑制策略的控制框图如图9所示。电流内环附加带通滤波器传递函数为
KBPF(s)=ξωcss2+ξωcs+ω2c (36) 在本文中,带通滤波器的中心频率设置为50 Hz,阻尼系数设置为0.7。考虑到滤波效果以及经济性,电压前馈环节采用二阶低通滤波器KLPF。
在电流内环附加带通滤波器后,MMC的阻抗特性如图10所示。
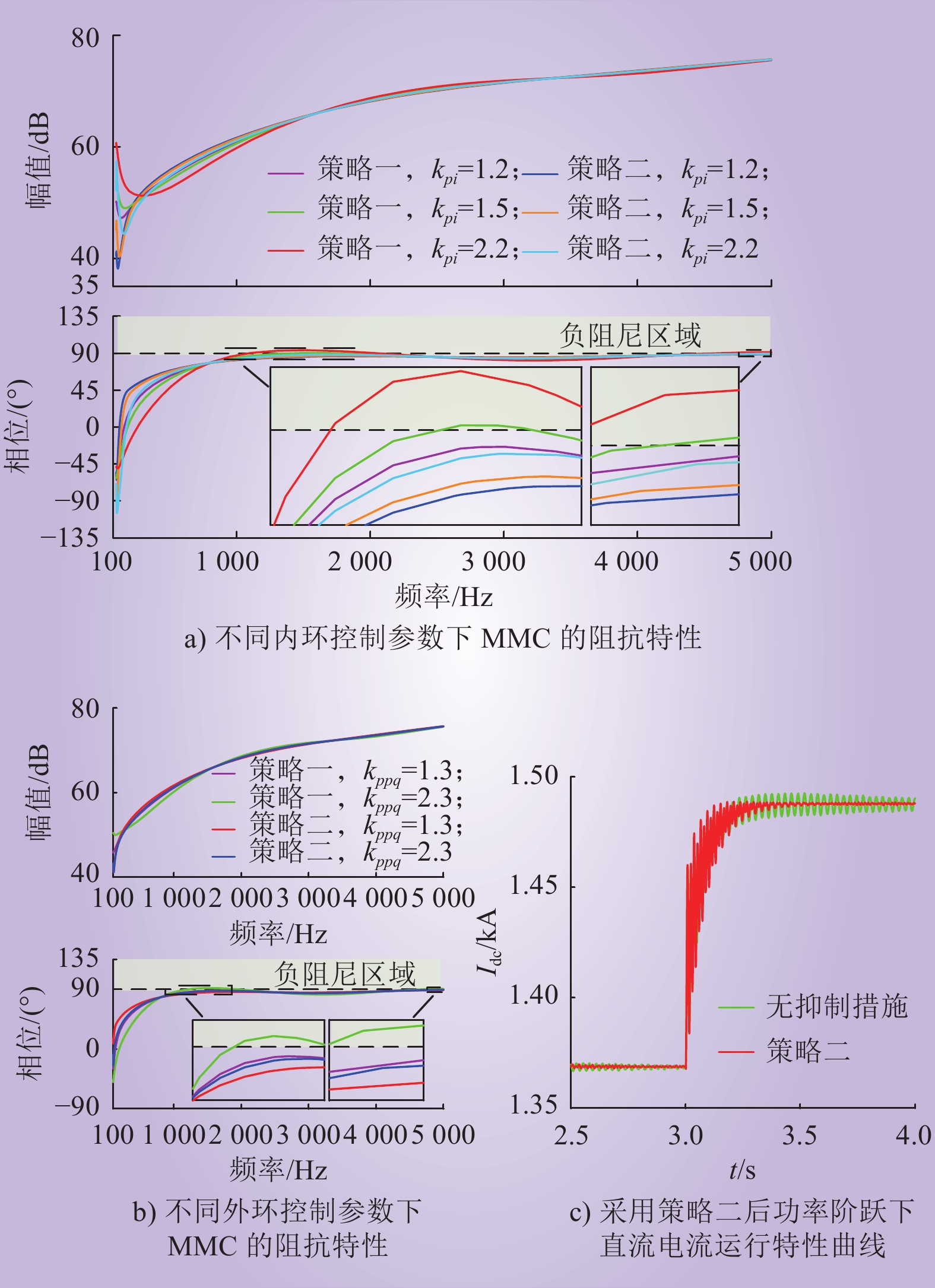
由图10可以看出:MMC的阻抗特性得到有效改善。但是该策略对控制器参数的选取要求较高,当电流内环的比例系数kpi=1.5时,采取该策略虽然可以提高系统的稳定性,但MMC的阻抗仍然存在负阻尼频段;虽然可以通过调整控制器参数消除振荡风险,但在复杂多端系统中对单个换流器进行参数优化,工作量过大,且应用场景受限,需要进一步探究提高系统稳定性的振荡抑制策略。
3.3 功率外环附加直流电流反馈的振荡抑制策略
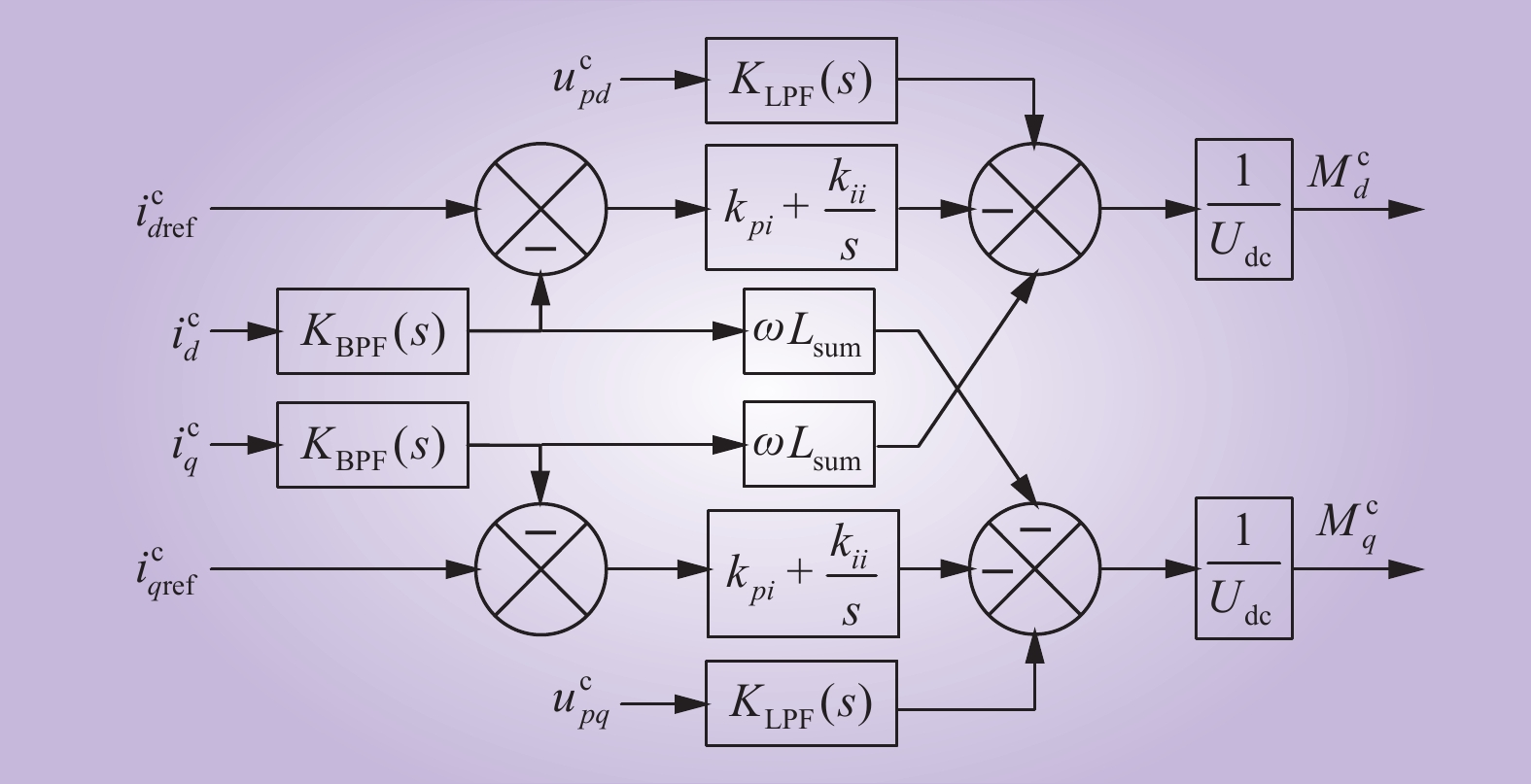
在策略一的基础上,考虑到功率外环对MMC阻抗特性的影响,提出了功率外环附加直流电流反馈的振荡抑制策略(下文称为“策略二”),该抑制策略的控制框图如图11所示。
功率外环附加直流电流反馈环节后,不同控制参数下MMC的阻抗特性以及当有功功率参考值发生阶跃变化后系统的运行特性曲线如图12所示。
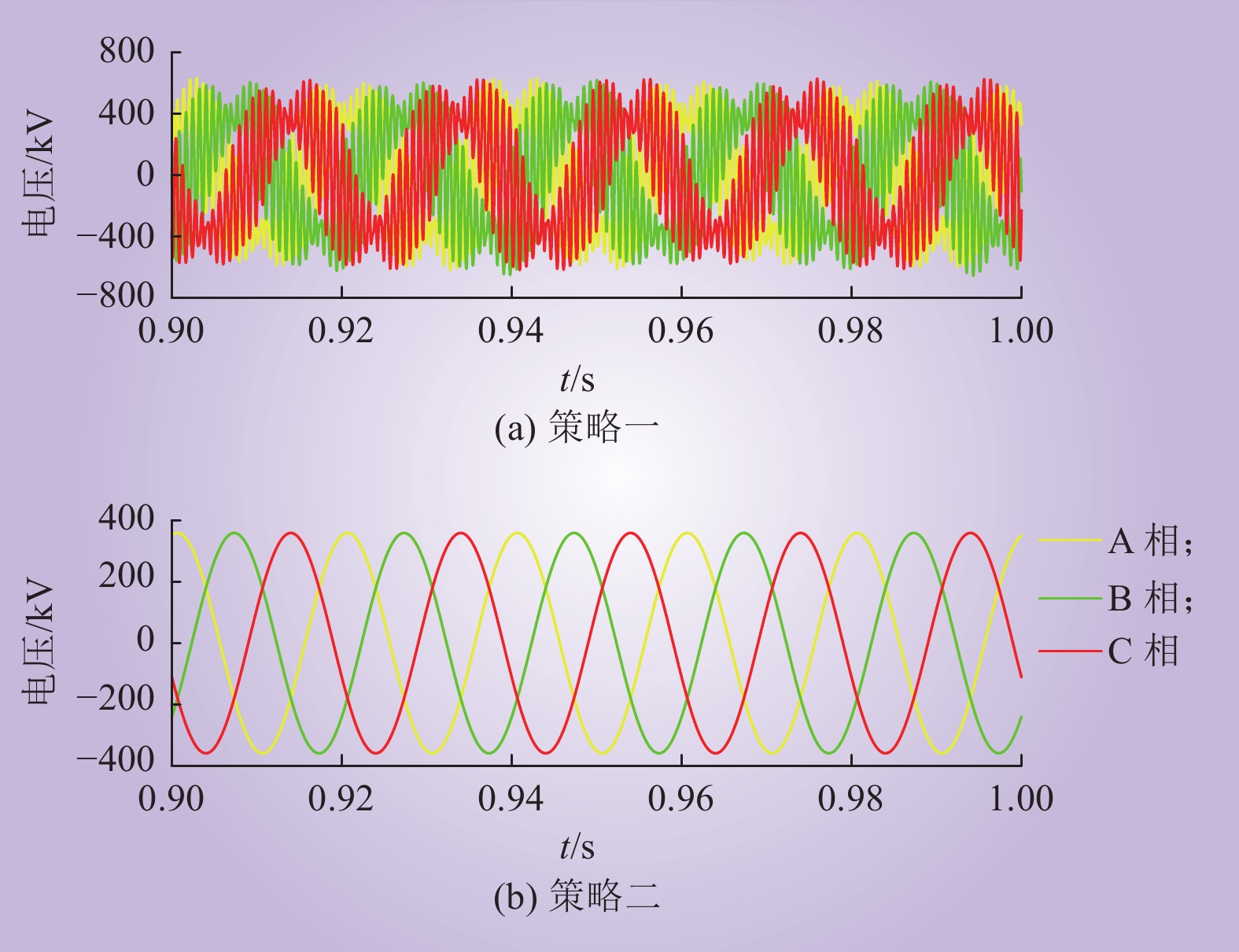
由图12可以看出:系统的稳定性进一步提升;策略二对系统的参数要求较低,在不同的控制参数下均能有效提高系统在中高频段的稳定性,更具有普适性;策略二对MMC阻抗的改善效果明显优于策略一,能达到消除特定振荡频段的目的。此外,在配置策略二后,系统的动态响应性能得到明显提升,系统在功率阶跃后能更快达到稳态。
4. 仿真验证
为验证本文建模及抑制策略的正确性和有效性,在PSCAD/EMTDC中搭建基于图1所建立的电磁暂态模型,模型参数设置见表1。
4.1 验证MMC建模的正确性
为了确保建立MMC阻抗模型时MMC基础时域模型的正确性,在Matlab中建立MMC的大信号、小信号模型。设置MMC换流站有功功率参考值Pref发生阶跃变化,2.1 s时Pref从1.0 p.u.阶跃为0.92 p.u.,3.2 s时恢复至1.0 p.u.,系统的大信号模型、小信号模型及电磁暂态仿真模型的运行特性曲线如图13所示。
图13中,LSM、SSM和EMT分别代表大信号模型、小信号模型和电磁暂态仿真模型的动态响应曲线。由图13可以得出:所建立的数学模型与电磁暂态模型的仿真结果基本吻合。各物理量在系统稳态运行时及控制量发生阶跃变化时均能准确反映系统运行特性,建立的小信号模型具有较高的准确性。
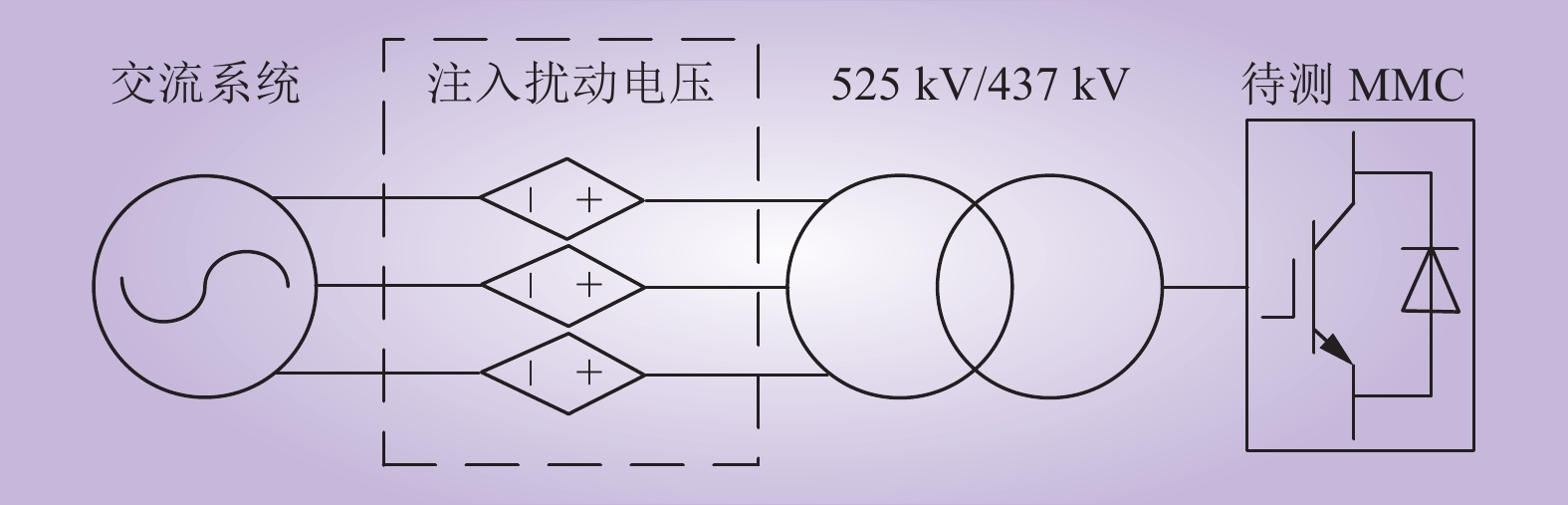
为验证阻抗模型的正确性,本文采用串联注入扰动电压的阻抗扫描法测量[0,
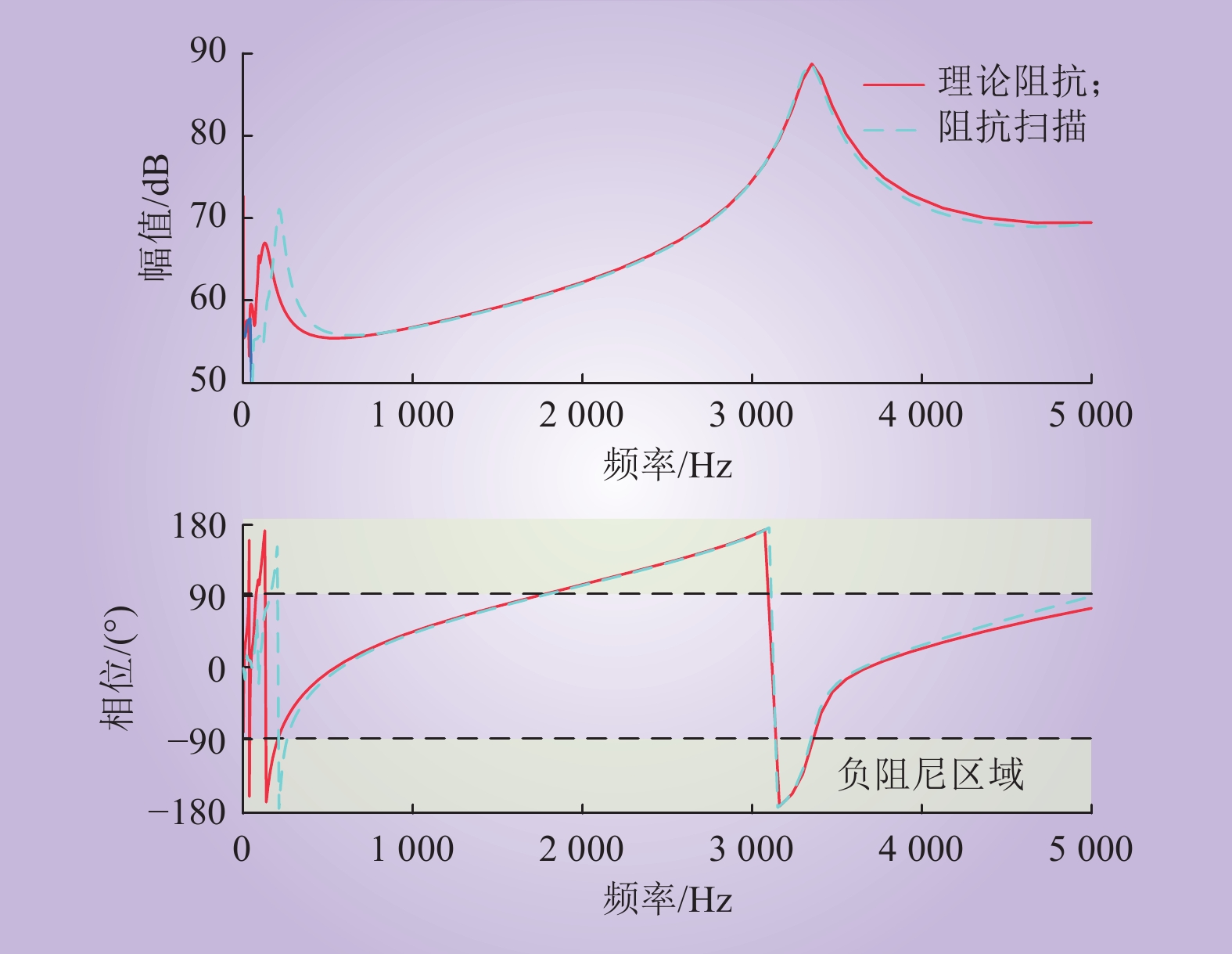
5000 Hz]频段下MMC的阻抗,扫频步长为50 Hz,仿真步长为10 μs。串联受控电压源注入不同频率的扰动电压后,对MMC网侧电压、电流进行正负序分离和快速傅里叶变换,将电压相量和电流相量相除即可得到MMC在不同频率下的阻抗。本文采用的阻抗扫描原理如图14所示。建立的MMC数学理论阻抗模型的阻抗特性曲线与在PSCAD/EMTDC中通过阻抗扫描方法得到的MMC正序阻抗的阻抗特性曲线如图15所示。
由图15可以看出:两条阻抗特性曲线基本吻合,建立的数学理论阻抗模型能较好地表征MMC中高频段的阻抗特性。
4.2 验证振荡抑制措施的有效性
为验证所提振荡抑制策略的有效性,本文对交流系统等效阻抗的建模方法参照文献[20]。
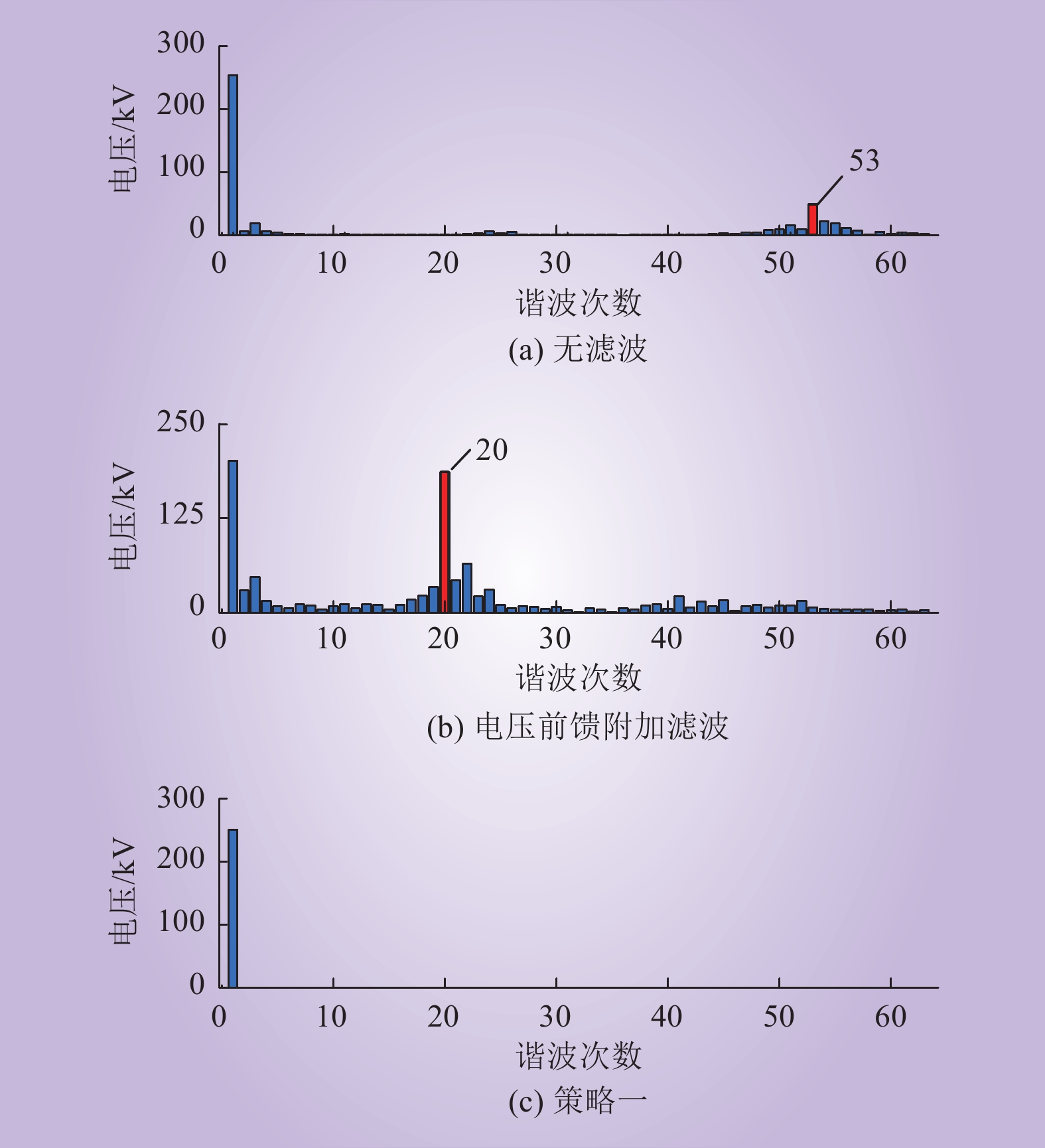
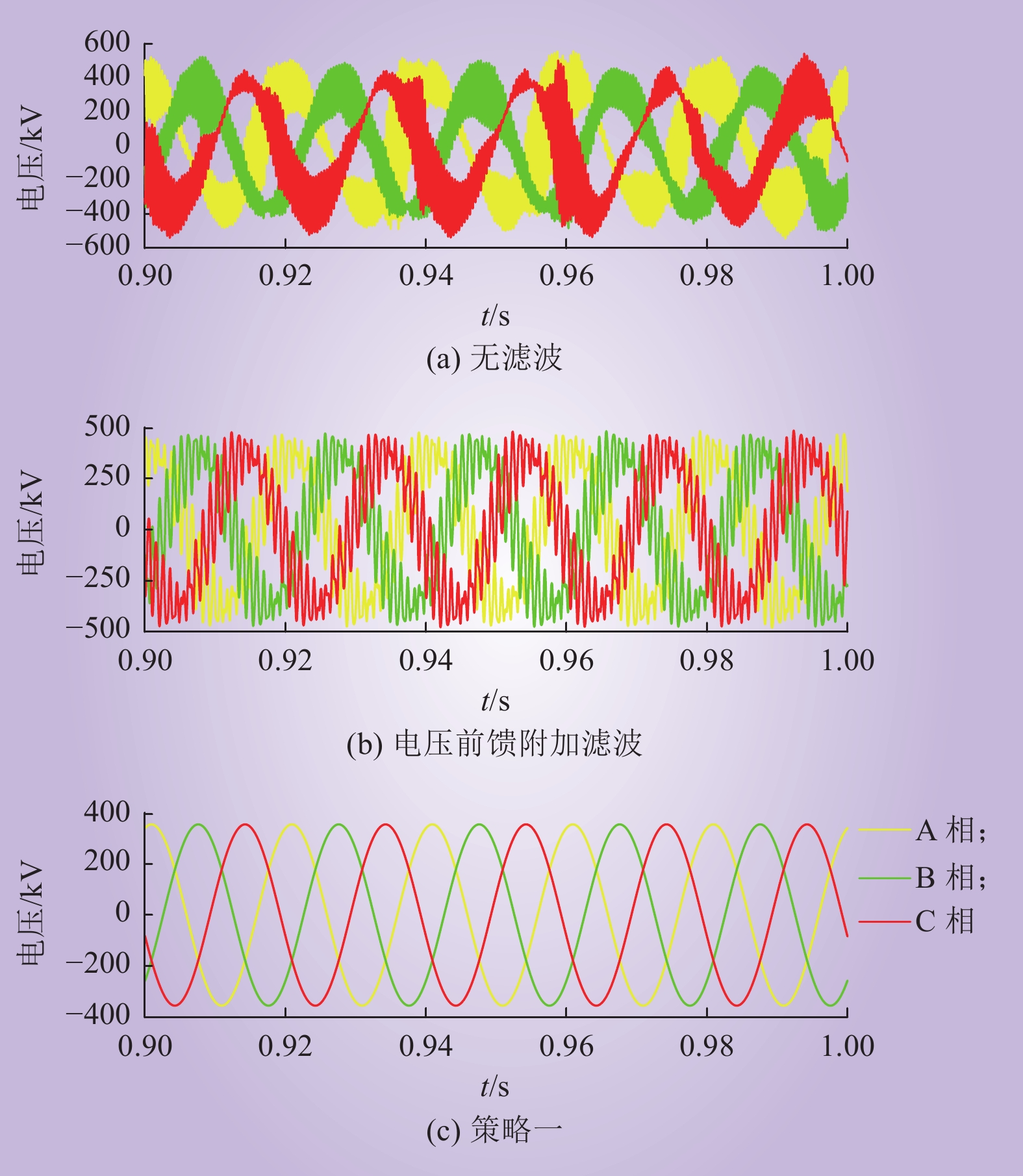
工况一:将交流系统的等效阻抗设置为2组串联的RL和C并联电路,其中:R1=0.1 Ω,R2=1 Ω,L1=L2=0.05 H,C1=0.6 μF,C2=0.1 μF。此时无抑制措施、电压前馈环节附加二阶低通滤波器、采用策略一时MMC与交流系统的阻抗特性图及仿真结果如图16~18所示。
当MMC不采取抑制措施时,阀侧交流电压发生振荡现象,谐波次数为53次左右,即发生2.6 kHz左右的振荡现象;在电压前馈环节二阶低通滤波器后,振荡频段发生转移,谐波次数为20次左右,即发生1 kHz左右的振荡现象;当采取抑制策略一后,系统的振荡现象消失,仿真结果与阻抗特性曲线的理论分析基本一致。
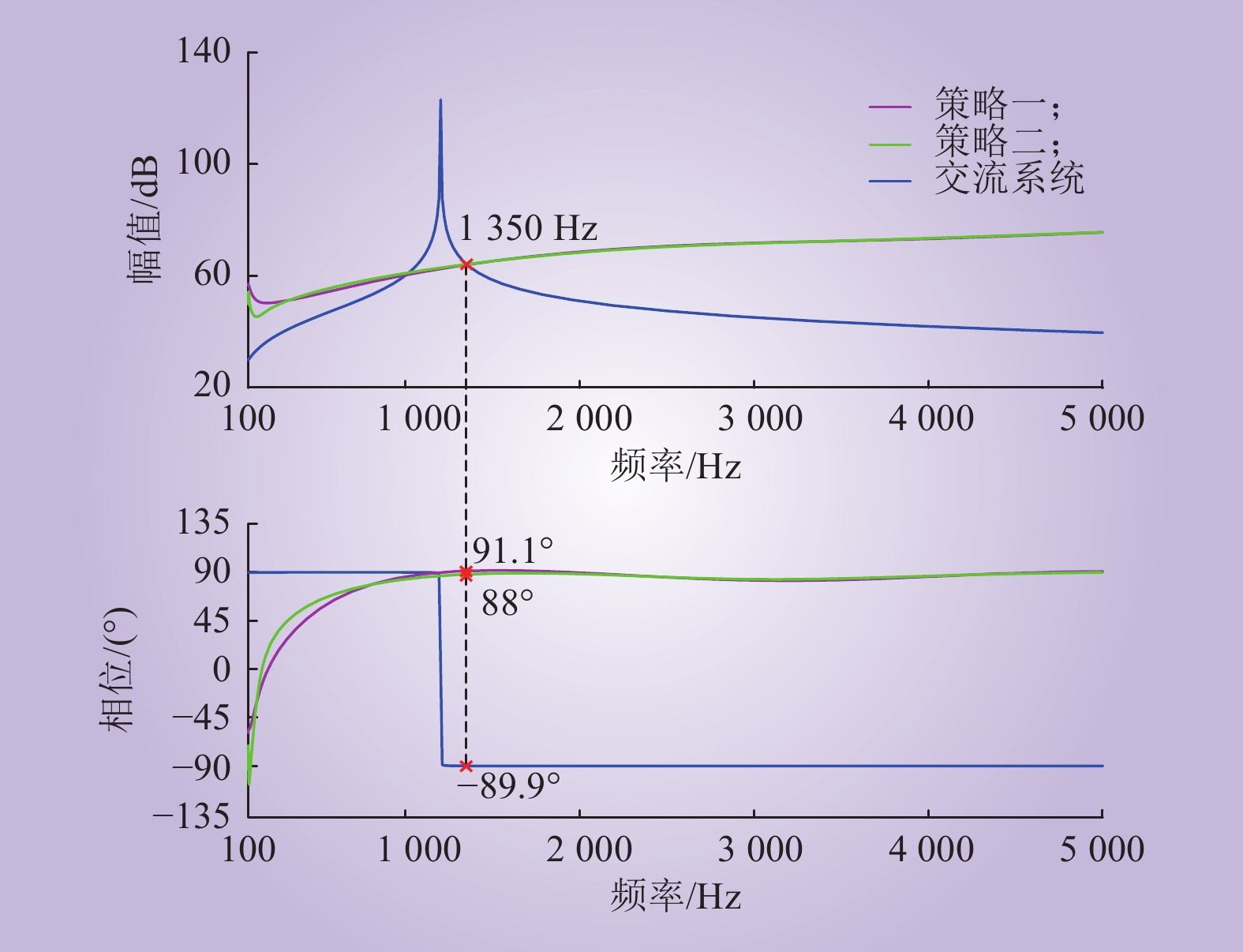
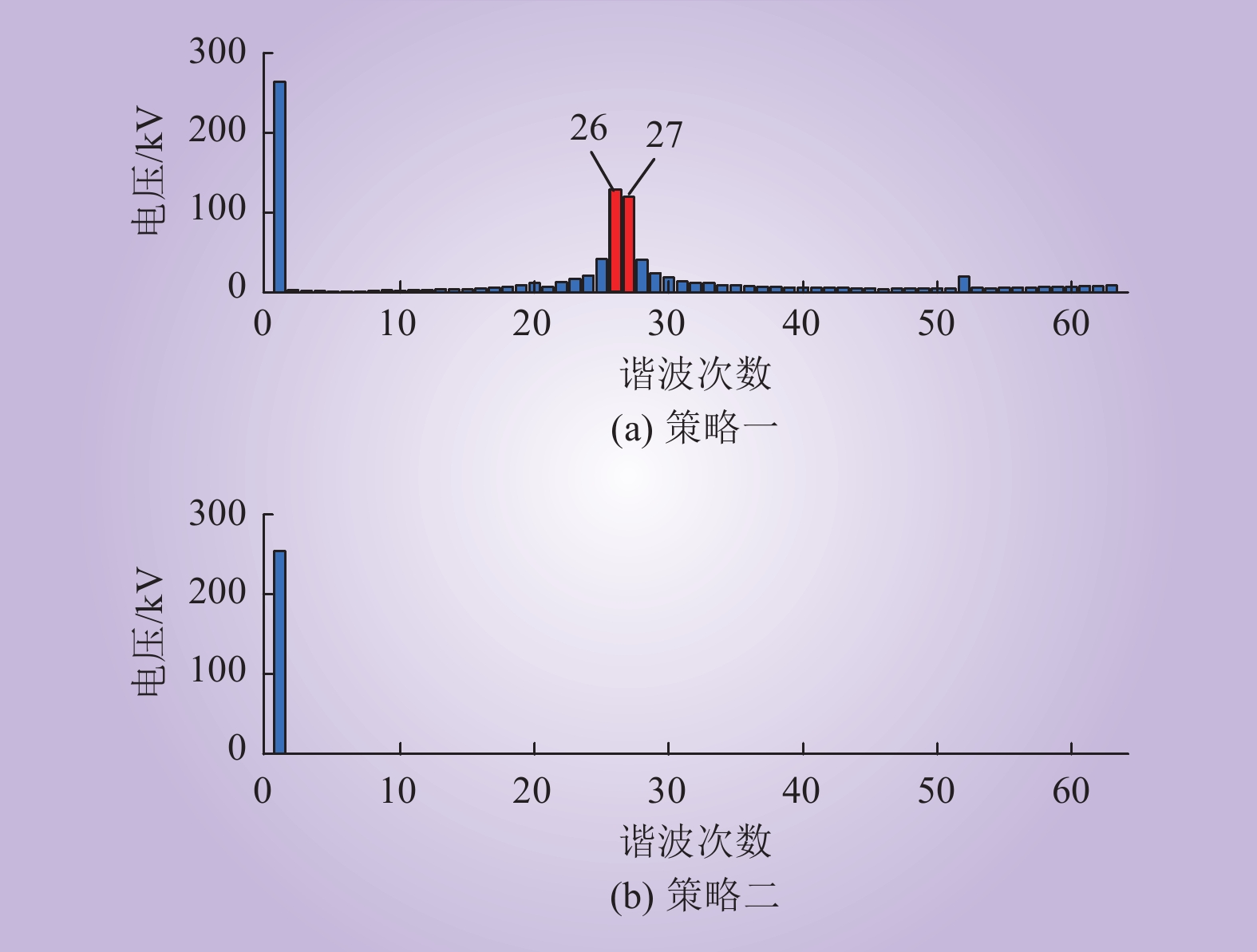
工况二:将交流系统的等效阻抗设置为1组RL和C并联电路,其中:R=0.1 Ω,L=0.05 H,C=0.35 μF。当策略一不能抑制振荡现象时采用策略二,此时MMC与交流系统的阻抗特性图及仿真结果如图19~21所示。
在采取策略一时,MMC的负阻尼频段没有被完全消除,如图19所示,MMC阻抗存在和交流系统阻抗相位差大于180°的频段,此时,阀侧交流电压发生振荡现象,谐波次数为27次左右,即发生1.35 kHz左右的振荡现象;当采取抑制策略二后,系统的振荡现象消失,仿真结果与阻抗特性曲线的理论分析基本一致。
5. 结论
1)功率外环、电流内环及控制链路延时对MMC阻抗特性的影响较大,在建模时不可忽略,通过在电压前馈环节附加滤波器可以提高系统的稳定性,但是无法完全消除系统存在的振荡风险。
2)基于电压前馈环节和电流内环的协同振荡抑制策略可以消除MMC阻抗的多个负阻尼频段,实现多频段振荡抑制,但是该方法对系统的参数有一定要求,当参数设置不当时,系统仍然可能发生振荡现象。
3)功率外环附加直流电流反馈的振荡抑制策略能改善MMC的负阻尼特性,大幅度提高系统的稳定裕度,有效提升系统的稳定性,并且能提升系统的动态响应速度。
-
表 1 系统主要参数
Table 1 Main parameters
参数 数值 系统参数 网侧交流电压/kV 525 额定直流电压/kV 840 额定功率/(MV·A) 1250 变压器 变压器变比/kV 525/437 变压器短路比/% 14 MMC 桥臂子模块数/个 500 桥臂等效电阻/Ω 0.5 桥臂等效电感/mH 140 桥臂子模块电容/μF 11000 控制器参数 锁相环PI参数(kpPLL、kiPLL) 2000 、3000 功率外环PI参数(kppq、kipq) 0.3、10 电流内环PI参数(kpi、kii) 0.4、16.7 环流抑制PI参数(kpi2、kii2) 0.4、40 Pade近似延时时间/μs 300 -
[1] 徐政, 薛英林, 张哲任. 大容量架空线柔性直流输电关键技术及前景展望[J]. 中国电机工程学报, 2014, 34(29): 5051–5062. XU Zheng, XUE Yinglin, ZHANG Zheren. VSC-HVDC technology suitable for bulk power overhead line transmission[J]. Proceedings of the CSEE, 2014, 34(29): 5051–5062.
[2] 马宁宁, 谢小荣, 贺静波, 等. 高比例新能源和电力电子设备电力系统的宽频振荡研究综述[J]. 中国电机工程学报, 2020, 40(15): 4720–4732. MA Ningning, XIE Xiaorong, HE Jingbo, et al. Review of wide-band oscillation in renewable and power electronics highly integrated power systems[J]. Proceedings of the CSEE, 2020, 40(15): 4720–4732.
[3] 徐政, 肖晃庆, 张哲任, 等. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017. [4] 谢小荣, 刘华坤, 贺静波, 等. 新能源发电并网系统的小信号阻抗/导纳网络建模方法[J]. 电力系统自动化, 2017, 41(12): 26–32. XIE Xiaorong, LIU Huakun, HE Jingbo, et al. Small-signal impedance/admittance network modeling for grid-connected renewable energy generation systems[J]. Automation of Electric Power Systems, 2017, 41(12): 26–32.
[5] ZOU C Y, RAO H, XU S K, et al. Analysis of resonance between a VSC-HVDC converter and the AC grid[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10157–10168. DOI: 10.1109/TPEL.2018.2809705
[6] 郭贤珊, 刘斌, 梅红明, 等. 渝鄂直流背靠背联网工程交直流系统谐振分析与抑制[J]. 电力系统自动化, 2020, 44(20): 157–164. GUO Xianshan, LIU Bin, MEI Hongming, et al. Analysis and suppression of resonance between AC and DC systems in chongqing-hubei back-to-back HVDC project of China[J]. Automation of Electric Power Systems, 2020, 44(20): 157–164.
[7] LI Y F, AN T, ZHANG D, et al. Analysis and suppression control of high frequency resonance for MMC-HVDC system[J]. IEEE Transactions on Power Delivery, 2021, 36(6): 3867–3881. DOI: 10.1109/TPWRD.2021.3049973
[8] 尹聪琦, 谢小荣, 刘辉, 等. 柔性直流输电系统振荡现象分析与控制方法综述[J]. 电网技术, 2018, 42(4): 1117–1123. YIN Congqi, XIE Xiaorong, LIU Hui, et al. Analysis and control of the oscillation phenomenon in VSC-HVDC transmission system[J]. Power System Technology, 2018, 42(4): 1117–1123.
[9] 王宇. 柔性直流接入的电网高频振荡阻尼控制策略及实时仿真研究[D]. 北京: 华北电力大学, 2021. WANG Yu. Research on active damping control and real-time simulation of high frequency resonance in grid-connected VSC-HVDC system[D]. Beijing: North China Electric Power University, 2021.
[10] JOVCIC D, JAMSHIDIFAR A. Phasor model of Modular Multilevel Converter with circulating current suppression control[C]//2015 IEEE Power & Energy Society General Meeting. Denver, CO, USA. IEEE, 2015.
[11] 朱蜀, 刘开培, 李彧野, 等. 基于动态相量及传递函数矩阵的模块化多电平换流器交直流侧阻抗建模方法[J]. 中国电机工程学报, 2020, 40(15): 4791–4805. ZHU Shu, LIU Kaipei, LI Yuye, et al. AC/DC-side impedance modeling method for modular multilevel converter based on dynamic phasors and transfer function matrix[J]. Proceedings of the CSEE, 2020, 40(15): 4791–4805.
[12] 鲁晓军, 林卫星, 安婷, 等. MMC电气系统动态相量模型统一建模方法及运行特性分析[J]. 中国电机工程学报, 2016, 36(20): 5479–5491, 5724. LU Xiaojun, LIN Weixing, AN Ting, et al. A unified dynamic phasor modeling and operating characteristic analysis of electrical system of MMC[J]. Proceedings of the CSEE, 2016, 36(20): 5479–5491, 5724.
[13] 李清, 张连升, 毛炽祖, 等. MMC-HVDC系统小信号阻抗建模及稳定性分析[J]. 南方电网技术, 2021, 15(7): 1–10. LI Qing, ZHANG Liansheng, MAO Chizu, et al. Small signal impedance modeling and stability analysis of MMC-HVDC system[J]. Southern Power System Technology, 2021, 15(7): 1–10.
[14] 冯俊杰, 邹常跃, 杨双飞, 等. 针对中高频谐振问题的柔性直流输电系统阻抗精确建模与特性分析[J]. 中国电机工程学报, 2020, 40(15): 4805–4820. FENG Junjie, ZOU Changyue, YANG Shuangfei, et al. Accurate impedance modeling and characteristic analysis of VSC-HVDC system for mid-and high-frequency resonance problems[J]. Proceedings of the CSEE, 2020, 40(15): 4805–4820.
[15] 于浩天, 吕敬, 厉璇, 等. 高频振荡抑制策略对柔性直流输电系统动态性能影响的综合评估[J]. 中国电机工程学报, 2022, 42(8): 2873–2889. YU Haotian, LYU Jing, LI Xuan, et al. Comprehensive evaluation of impact of high-frequency oscillation suppression strategy on the dynamic performance of flexible HVDC transmission system[J]. Proceedings of the CSEE, 2022, 42(8): 2873–2889.
[16] 彭意, 郭春义, 杜东冶. 柔性直流输电的阻抗重塑及中高频振荡抑制方法[J]. 中国电机工程学报, 2022, 42(22): 8053–8063. PENG Yi, GUO Chunyi, DU Dongye. Research on medium and high frequency oscillation suppression approach based on impedance tuning in flexible HVDC system[J]. Proceedings of the CSEE, 2022, 42(22): 8053–8063.
[17] 吴汪平, 解大, 赵祖熠, 等. 双馈型风电系统变流器控制参数对振荡模态的影响[J]. 电机与控制应用, 2017, 44(7): 98–107. WU Wangping, XIE Da, ZHAO Zuyi, et al. Analysis of influence of doubly fed wind power system PI converter control parameter on oscillation mode[J]. Electric Machines & Control Application, 2017, 44(7): 98–107.
[18] 郭琦, 郭海平, 黄立滨. 电网电压前馈对柔性直流输电在弱电网下的稳定性影响[J]. 电力系统自动化, 2018, 42(14): 139–144. GUO Qi, GUO Haiping, HUANG Libin. Effect of grid voltage feed forward on VSC-HVDC stability in weak power grid[J]. Automation of Electric Power Systems, 2018, 42(14): 139–144.
[19] MAN J F, CHEN L, TERZIJA V, et al. Mitigating high-frequency resonance in MMC-HVDC systems using adaptive Notch filters[J]. IEEE Transactions on Power Systems, 2022, 37(3): 2086–2096. DOI: 10.1109/TPWRS.2021.3116277
[20] 李国庆, 王延旭, 辛业春, 等. 基于附加级联陷波滤波器的MMC-HVDC多频段谐振抑制策略[J]. 电力自动化设备, 2023, 43(4): 10–15. LI Guoqing, WANG Yanxu, XIN Yechun, et al. Multi-band resonance suppression strategy for MMC-HVDC based on additional cascaded Notch filters[J]. Electric Power Automation Equipment, 2023, 43(4): 10–15.
[21] ZHU S, LIU K P, QIN L, et al. Reduced-order dynamic model of modular multilevel converter in long time scale and its application in power system low-frequency oscillation analysis[J]. IEEE Transactions on Power Delivery, 2019, 34(6): 2110–2122. DOI: 10.1109/TPWRD.2019.2900070
[22] 李云丰, 赵文广, 贺之渊, 等. 连接弱交流电网的柔性直流换流站外环控制器参数解析计算及其限制因素分析[J]. 中国电机工程学报, 2023, 43(24): 9682–9696. LI Yunfeng, ZHAO Wenguang, HE Zhiyuan, et al. Analytical calculation method of outer loop controller parameters of HVDC converter station connected to weak AC grid and analysis of limiting factors[J]. Proceedings of the CSEE, 2023, 43(24): 9682–9696.




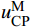

 下载:
下载:
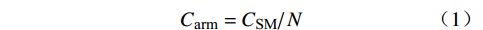
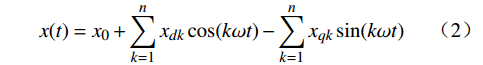
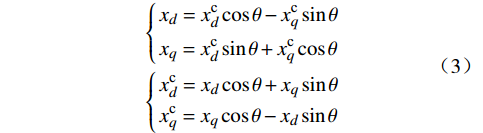
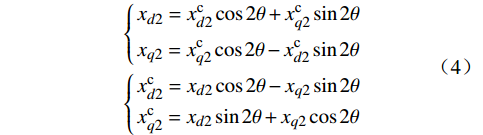
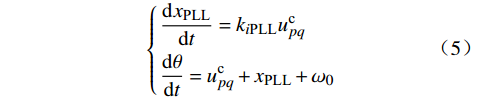
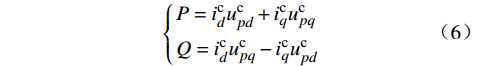
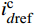
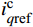
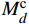
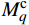
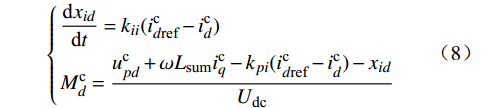
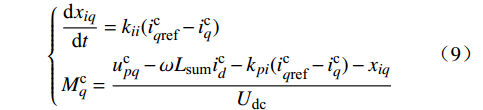
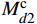
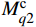
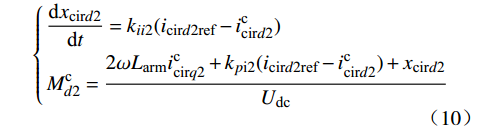
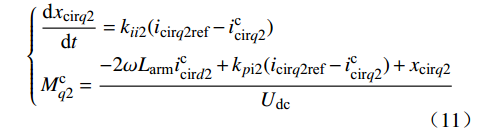
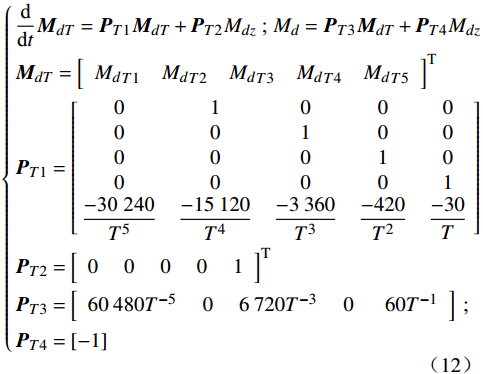
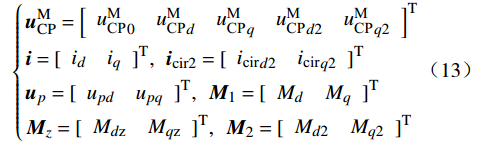

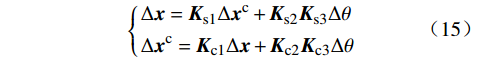
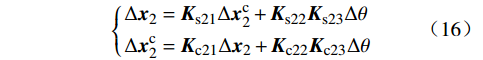
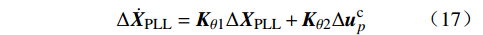
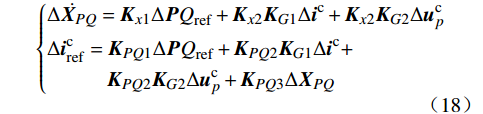
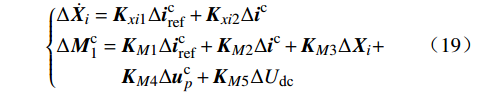
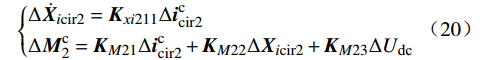
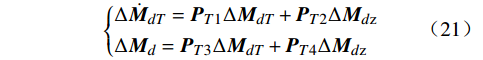
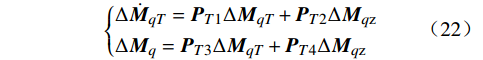

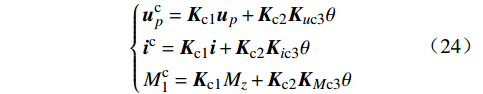
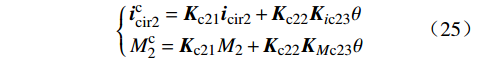
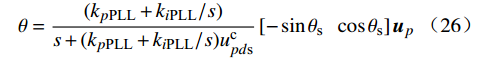
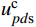
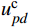
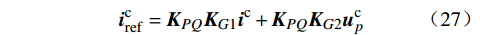
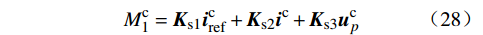
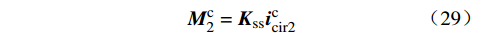
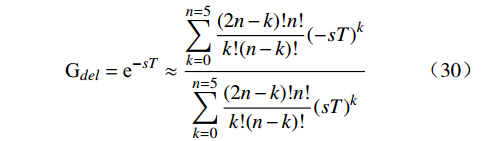

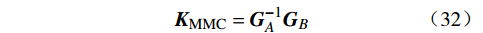
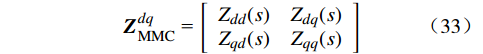
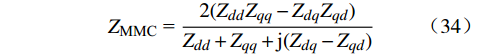


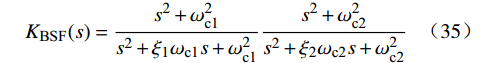
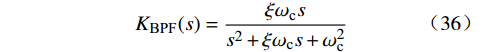




 下载:
下载:



