0.   引言

为落实碳达峰碳中和战略目标，我国正在加快推进沙漠、戈壁和荒漠地区大型风光基地建设，2030年，将规划建设新能源发电基地总装机约4.55亿kW^[1-2]。基于模块化多电平换流器(modular multilevel converter，MMC)的高压直流输电具备控制方式灵活、谐波含量低、可实现新能源场站孤岛运行等优势，在我国南澳多端、如东海风等工程中得到广泛应用^[3-4]，为我国沙戈荒等地区的大规模光伏开发及电力远距离外送提供了技术支撑，具有广泛的发展前景。

沙戈荒地区位于我国西部，采用架空线传输直流故障发生概率高，其直流故障电流上升率可以达到3 kA/ms，在故障后几ms内绝缘栅双极晶体管(insulate gate bipolar transistor，IGBT)电流应力将越限^[5]，导致子模块闭锁，因此可靠的直流故障穿越方案成为制约柔直发展的因素之一。

直流断路器(DC circuit breaker，DCCB)是目前直流故障清除的关键设备之一，可以大幅降低直流故障清除时间，实现直流系统的不闭锁、不停运工作^[6-8]。但是直流断路器尚无800 kV级别的产品，其在特高压输电场景下的应用还需要进一步研究，而半全混合MMC方案已经证明了其在特高压场景下的适用性，成为沙戈荒外送工程中的优选方案。

半全混合型MMC(简称混合MMC)具备交直流电压解耦能力，可以在维持交流电压支撑能力的同时实现直流故障的无闭锁穿越^[9-13]。但是，现有工程的全桥比例显著偏高，昆柳龙工程中全桥子模块(full bridge sub-module，FBSM)占比高达70%^[14]，大大增加了投资成本，运行损耗也是半桥MMC的1.3倍以上^[15-16]。因此，成本与损耗方面的不足限制了混合MMC的进一步发展。

在此基础上，混合MMC中FBSM占比的降低成为了关注的重点。我国即将建设的甘浙直流也将采用混合MMC方案，其规划的FBSM比例为60%，但在特高压、大容量送出场景下，若可以进一步降低FBSM占比，则会显著增加该方案的经济效益。目前对于低全桥比例混合型MMC的研究尚属起步阶段，文献[17]通过在桥臂电压调制波中注入三倍频电压分量，将全桥子模块的配置比例由50%下降至43.3%，但该方法下全桥比例的降低空间有限，且尚无实际工程应用；文献[18]提出了一种所需FBSM比例较低的混合型MMC，通过加入交流侧阻断开关来减少闭锁期间交流侧馈入的能量，但是该方案在故障穿越期间使MMC闭锁，无法满足换流站交流侧无功功率的不间断传输。因此，低全桥比例的混合型MMC仍有较大的研究空间。

本文首先提出一种协同调制波自适应限幅的改进定直流电流控制方法，通过调制波限幅的方式短时削弱混合MMC对交流侧的电压支撑能力，提升低全桥比例下混合MMC的直流负压生成能力，实现直流故障的清除；其次，分析该故障穿越方法下的FBSM充电过程，为防止故障穿越过程中的FBSM过电压，提出一种气隙、避雷器协同耗能的子模块过电压抑制方案；最后，在仿真系统中搭建不同比例下混合型MMC的仿真模型，对比验证所提方案的有效性。

1.   低全桥比例混合型MMC故障清除方案

1.1   混合型MMC直流故障清除原理

图 1为混合MMC拓扑及其在稳态、降压和故障穿越期间的核心波形。与传统半桥型MMC相比，混合型MMC可以按照运行需求改变直流侧电压，且同时具备交流侧电压支撑能力。其交流电压峰值U_sm与直流电压实际输出值U_dc如式(1)所示。

图  1  混合MMC拓扑及多工况波形

Figure  1.  Hybrid MMC and multi-condition waveforms

下载: 全尺寸图片 幻灯片

式中：M_ac为交流调制比；M_dc为直流调制比；U_dcN为额定直流电压。

以a相为例，桥臂电压u_xa(x = p, m)的取值范围如式(2)所示。

其中，直流电压调制比M_dc = 1表示稳态运行工况，M_dc < 1表示降直流电压运行或直流故障处理工况。

由式(2)可知，当M_dc < M_ac时，桥臂电压会出现负值，此时桥臂中FBSM负向投入，输出负电压。直流电压调制比M_dc(< 0)越小，则故障清除速度越快。若故障穿越期间M_dc最小值可达到M_{dc_min}，则混合型MMC桥臂中FBSM的数量至少要满足：

式中：N为桥臂子模块总数；N_F为FBSM数目。

若取交流调制比M_ac = 1，则混合型MMC可输出的最小直流电压U_{dc_min}可以表示为

式中N_H为HBSM数目。

由式(4)可知，全桥占比N_F/N与U_{dc_min}呈反比关系。在传统认知中(不考虑三次谐波电压注入的影响)，当N_F/N ≥ 50%时，直流侧可以输出零电压或者负电压，用于直流故障的清除；当N_F/N < 50%，无法稳定输出零/负直流电压，无法满足直流故障穿越的需求。

1.2   低全桥比例混合型MMC直流故障清除方案

降低全桥占比可以显著降低子模块混合型MMC换流器的制造成本，具有较高的经济效益。由上述稳定运行特性分析可知，直流侧零/负电压的输出限制了FBSM比例的降低。为在低全桥比例情况下仍可以输出零/负直流电压，可以在故障穿越期间将6个桥臂的FBSM按照相位顺序依次整体负投入一段时间，并限制其对应上/下桥臂子模块的正向投入，通过短时削弱对交流侧的电压支撑能力，实现直流侧故障电流的衰减。

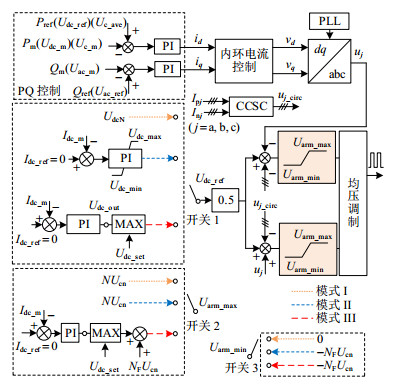
低全桥比例混合型MMC的控制器结构如图 2所示，包含内环电流控制器与外环功率控制器，其中外环功率控制器的有功类控制目标可以选择有功功率P_m、直流电压U_{dc_m}和子模块电容电压平均值U_{c_m}，无功类控制目标可以选择无功功率Q_m和交流电压幅值U_{ac_m}。PLL和CCSC分别为锁相和环流抑制环节。

图  2  混合型MMC控制策略

Figure  2.  Hybrid MMC control strategy

下载: 全尺寸图片 幻灯片

图 2控制器中有3个选择开关。开关1为桥臂直流电压参考值U_{dc_ref}选择开关，开关2为桥臂电压调制波上限值U_{arm_max}选择开关，开关3为桥臂电压调制波下限值U_{arm_min}选择开关。开关1—3均根据3种运行模式进行切换，模式Ⅰ为稳态控制(黄色)，模式Ⅱ为传统故障穿越控制(蓝色)，模式Ⅲ为本文所提故障穿越控制(红色)。

1）模式Ⅰ：定直流电压控制。额定直流电压U_dcN作为直流电压参考值U_{dc_ref}，桥臂电压的输出区间为[0, NU_cn]，其中U_cn为子模块电容电压额定值。

2）模式Ⅱ：定直流电流控制^[11]。故障检测后，电流参考值I_{dc_ref}置0，与故障电流I_{dc_m}比较后经PI控制器得到U_{dc_ref}，如式(5)所示。U_{dc_ref}取值区间为[U_{dc_min}, U_{dc_max}]，其中U_{dc_min}由式(4)得到。该模式下桥臂电压的输出区间为[−N_FU_cn, NU_cn]。

3）模式Ⅲ：协同调制波自适应限幅的改进定直流电流控制。I_{dc_ref}与I_{dc_m}比较后经PI控制器得到U_{dc_out}，与设定值U_{dc_set}(负值)比较后得到U_{dc_ref}。通过合理设定U_{dc_set}，直流电流衰减初期U_{dc_ref}由直流电压设定值U_{dc_set}主导生成；直流电流衰减近0时，U_{dc_out}逐渐回归至0附近，主导生成U_{dc_ref}，如式(6)所示。该模式下桥臂电压最小值为桥臂最小可输出负压−N_FU_cn，最大值U_{arm_max3}由式(7)生成。

对比模式Ⅱ，模式Ⅲ加入了电压比较环节，其直流负压最小值U_{dc_set}不再受式(4)限制，可以人为设定。在此基础上，为使实际输出直流电压可以跟随U_{dc_ref}，模式Ⅲ改进了模式Ⅰ、Ⅱ中的调制波限幅环节，下限由桥臂负压生成能力决定，上限则配合U_{dc_ref}的变化，限制桥臂子模块正向投入的能力。

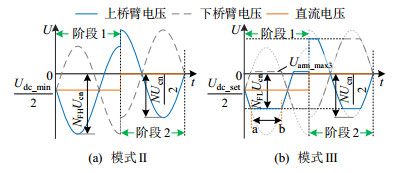
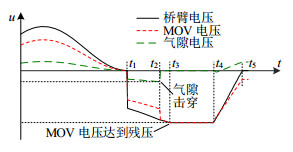
为更直观表达传统控制模式Ⅱ与本文所提控制模式Ⅲ的区别，在故障穿越能力一致的前提下(图 2中开关1选择模式Ⅱ的负压最小值U_{dc_min}与选择模式Ⅲ的负压最小值U_{dc_set}相等)，绘制故障穿越期间的桥臂电压波形，如图 3所示。在故障穿越初期，U_{dc_ref}选择环节中PI控制器输出小于U_{dc_min}或U_{dc_set}，U_{dc_ref}为负压最小值，将该阶段定义为阶段1；当故障电流I_{dc_m}逐渐衰减至0附近时，PI控制器输出值逐渐自适应恢复至0，U_{dc_ref}也变为0，将该阶段定义为阶段2。

图  3  故障穿越期间桥臂电压波形

Figure  3.  Arm voltage waveforms during fault ride-through

下载: 全尺寸图片 幻灯片

图 3(a)为模式Ⅱ下故障穿越期间的桥臂电压波形图，其中N_FH为桥臂配置的FBSM个数。阶段1中U_{dc_ref} = U_{dc_min}，桥臂电压极小值为−N_FHU_cn；阶段2中U_{dc_ref} = 0，桥臂电压极小值为−NU_cn/2。由图 3(a)可知，N_FHU_cn ≥ NU_cn/2，其中，当U_{dc_min}取0时，N_FHU_cn = NU_cn/2，因此N_FH/N ≥ 50%。在整个故障穿越过程中，直流侧电压的改变并不影响混合MMC对交流侧的电压支撑能力。

图 3(b)为模式Ⅲ下故障穿越期间的桥臂电压波形图，其中N_FL为桥臂配置的FBSM个数。阶段1中U_{dc_ref} = U_{dc_set}，桥臂电压下限值为−N_FLU_cn，桥臂电压上限值U_{arm_max3}与下限值−N_FLU_cn以U_{dc_ref} /2为轴相对称。以图 3(b)中a—b时间段为例，此时上桥臂电压受下限值约束，负投入该桥臂全部N_FL个FBSM；下桥臂受上限值约束，限制子模块正投入数量，以满足负直流电压需求。阶段2中U_{dc_ref} = 0，桥臂电压下限值保持不变，桥臂电压上限值跟随U_{dc_ref}变化。由图 3(b)可知，N_FLU_cn < NU_cn/2，因此N_FL/N < 50%。

模式Ⅲ通过桥臂电压自适应限幅环节与负直流电压参考值相配合，将调制波由正弦波(模式Ⅱ)变为平顶波(模式Ⅲ)，一定程度上削弱了混合MMC对交流侧的电压支撑能力。阶段1(U_{dc_ref} = U_{dc_set})与阶段2(U_{dc_ref} = 0)中，交流电压波形畸变时间均仅维持数ms，且畸变程度较小，因此若送端采用跟网型新能源机组，混合型MMC交流电压支撑能力的削弱对机组运行的影响可近似被忽略。

综上所述，采用模式Ⅱ仅适用于传统比例(N_F/N ≥ 50%)下的直流故障穿越，而模式Ⅲ还可应用于低全桥比例(N_F/N < 50%)情况。因此在低全桥比例情况下，可以选择模式Ⅲ用于直流故障穿越。

2.   低全桥比例下全桥子模块过电压分析

在FBSM全部负投入阶段，若上桥臂电流I_{a_up}为负(流动方向由下至上)，则I_{a_up}持续对FBSM充电，可能导致FBSM过电压而闭锁。以a相为例，模式Ⅲ下，故障穿越初期上桥臂FBSM全部负向投入，下桥臂限制子模块正向投入，如图 3(b)中a—b时段所示。

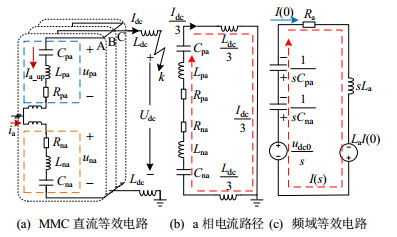
直流故障发生后，a—b时间段直流侧等效电路图如图 4(a)、(b)所示。图 4(b)中：L_pa、R_pa、C_pa分别为a相上桥臂的电感与电阻；L_na、R_na、C_na分别为a相下桥臂的电感与电阻。

图  4  混合型MMC直流侧等效电路图

Figure  4.  DC side equivalent circuit diagram of hybrid MMC

下载: 全尺寸图片 幻灯片

若单个子模块电容为C₀，则a—b阶段a相上桥臂的等效子模块电容C_pa为

该阶段下桥臂投入的全/半桥子模块数量可以表示为

其中，若N_na > 0，则下桥臂正投入HBSM/FBSM，反之负投入FBSM。则a相下桥臂的等效子模块电容C_na可以表示为

故障穿越期间，忽略短时间内交流侧的能量馈入，衰减的故障电流I_dc会对FBSM电容进行充电，电容电压将会上升。

令：

且：

对图 4(b)列写KVL方程可得：

式中：u_{c_pa}为a相上桥臂投入子模块电压之和，其a—b时间段内的初始值为u_p0；u_{c_na}为a相下桥臂投入子模块电压之和，其a—b时间段内的初始值为u_n0。若忽略桥臂电抗压降以及子模块器件压降，则u_p0与u_n0之和为直流侧电压的初始值u_dc0。

为简化计算和分析，将式(13)转化为频域形式：

由式(14)可得图 4(b)电路的频域形式，如图 4(c)所示，则直流电流的频域表达式I(s)为

因此，上桥臂电压增量为

此电压增量方向如图 4(c)中绿色线条所示，可以看出，若直流侧电压的初始值u_dc0为负，上桥臂电压u_pa的绝对值将增大，每个FBSM的电压也将上升。FBSM电容电压增量可以表示为

规定ΔU_F(t)为ΔU_F(s)的时域表达形式，由式(17)可知，ΔU_F的大小与电气量L_a、R_a、C₀成反比，与初始值I(0)、u_dc0成正比。故障穿越策略模式Ⅲ刚投入时，I(0)最大，因此故障穿越期间首先全部负向投入FBSM的桥臂子模块过压最严重。

在模式Ⅱ中，采用相同的分析方法，对于相同的I(0)、u_dc0，子模块电容的电压增量可表示为

式(18)分母中s²与s的系数均为式(17)的2倍，常数项相较式(17)仅相差N_na的绝对值，由于过电压暂态过程中高频分量更多，因此s²与s的系数对电压增量的影响更显著，而常数项对于增幅的影响非常小。故式(18)子模块电容电压增量小于式(17)，采用模式Ⅲ的FBSM过压程度要大于模式Ⅱ情况。之所以出现该现象，是因为在低全桥比例下，模式Ⅲ上桥臂故障初期负投入了所有的FBSM，在整个a—b时间段内FBSM均处于充电状态；而在传统比例下，模式Ⅱ中FBSM仍可以动态投切，当桥臂处于充电状态时，可以将电压较大的FBSM旁路，进而以较多的FBSM承担与低全桥比例相同的故障能量，因此子模块过电压程度要更低。

综上所述，采用协同调制波自适应限幅的改进定直流电流控制可能会导致FBSM过电压问题，且桥臂电压U_arm首先达到−N_FU_cn的桥臂FBSM过电压最严重，为此有必要加入子模块过电压抑制策略。

3.   基于辅助耗能装置的过电压抑制方法

金属氧化物避雷器(metal oxide varistor，MOV)是广泛采用的过电压抑制手段，较多应用于断路器的耗能回路中^[19]。MOV的非线性特性用α = V_RES/V_REF表示，一般取值为1.6。

目前直流输电工程中广泛采用4.5 kV/3 kA的IGBT器件，然而对于超大容量的MMC系统而言，稳态下桥臂电流有效值将达到3.1 kA左右，额定电流3 kA的IGBT器件已无法满足系统要求。目前已生产出4.5 kV/5 kA的IGBT器件，可以满足超大容量MMC的安全运行需求，因此本文均针对4.5 kV/5 kA的IGBT器件展开讨论。

对于选择4.5 kV/5 kA IGBT的子模块而言，稳态下子模块额定电压U_cn可取2.2 kV；故障时为防止子模块闭锁，需满足最大子模块电压U_cmax < 3.1 kV^[20]。若设定MOV残压V_RES = 3.1 kV，则V_REF为

即在稳态下MOV回路中将会流过电流，不仅影响桥臂正常工作，也将导致MOV快速老化。现有MOV非线性曲线难以满足子模块电压的保护需求，为抑制FBSM的过电压，本文添加非线性曲线可调制的辅助耗能设备，耗散掉直流故障穿越期间的故障能量。

3.1   辅助耗能装置拓扑结构

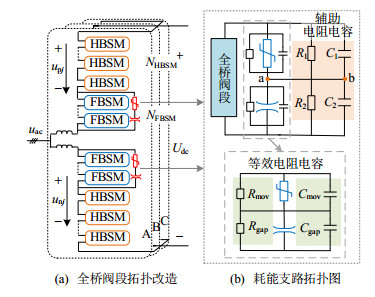
为改善MOV的非线性特性，可以采用MOV、气隙串联结构与全桥阀段并联的拓扑改造辅助耗能方案，如图 5(a)所示。稳态下气隙不被击穿，气隙与MOV共同承担正向的全桥阀段电压；故障发生后，气隙电压达到其击穿电压后首先被击穿，负向升高的全桥阀段电压全部由MOV承担，此时MOV可以有效限制全桥阀段电压，进而达到限制FBSM电容电压、消耗故障能量的目的。

图  5  MMC换流器桥臂级拓扑改造图

Figure  5.  Diagram of the arm-level topology of the MMC

下载: 全尺寸图片 幻灯片

辅助耗能装置的详细结构如图 5(b)所示，其中：R_gap为气隙的导通电阻，未击穿时近似开路，击穿后近似短路；C_gap为气隙的等效电容，为pF级；R_mov为MOV的等效可变电阻，稳态下为MΩ级，当MOV两端电压逐渐增大，R_mov逐渐减小，为能量流通提供通路；C_mov为MOV的寄生电容，远大于C_gap，为nF级。

稳态运行工况下，气隙与MOV共同承担桥臂电压，为实现MOV与气隙间电压的合理分配，可以在MOV与气隙两端分别并联辅助电阻R₁、R₂。由于C_mov ≫ C_gap，稳态工况下，近似正弦波的全桥阀段电压几乎由气隙全部承担，导致气隙的反复击穿，因此可以在MOV与气隙两端分别并联辅助电容C₁、C₂，以消除寄生电容的影响，且C₁ ≫ C_mov、C₂ ≫ C_gap，通过并联电容主导下的分压，改变气隙和MOV在稳态时的分压，进而避免气隙击穿；同时C₁、C₂远小于桥臂等效电容最小值C_{arm_min}，即桥臂子模块全部投入后的桥臂等效电容，不会影响桥臂的正常工作。值得注意的是，电阻R₁、R₂大小之比应与电容C₁、C₂大小之比互为倒数，避免因图 5(b)耗能回路中a、b点电位不同而引发电容的充放电，进而导致气隙的反复击穿。

3.2   辅助耗能装置的动作过程分析

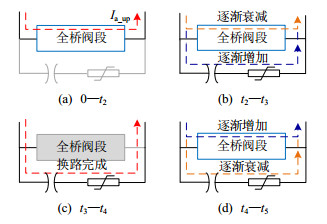
辅助耗能装置在故障耗能阶段的动作过程如图 6所示。

图  6  动作时序图

Figure  6.  Action timing diagram

下载: 全尺寸图片 幻灯片

1）0—t₁：稳态运行工况。FBSM作半桥使用，仅有正投入与旁路两种状态，气隙不放电。MOV与气隙共同承担全桥阀段电压。该阶段桥臂电流流经MMC全桥阀段。

2）t₁—t₂：t₁时刻，检测到直流故障，故障穿越策略投入。气隙与MOV的负向电压同步上升，该阶段桥臂电流仍流经MMC全桥阀段。t₂时刻气隙达到其击穿电压而被击穿。

3）t₂—t₃：忽略电弧电压，t₂时刻后上升的全桥阀段负电压全部由MOV承担，t₃时刻MOV的电压上升至其残压。该阶段桥臂电流由MMC全桥阀段转移至MOV回路。由于MOV的并联电容C₁远小于全桥阀段的等效电容最小值C_{arm_min}，因此可以近似忽略流经并联电容C₁的桥臂电流。

4）t₃—t₄：MOV限制过电压并吸收故障能量，其中FBSM电容电压最大值V_cmax不超过3.1 kV，全桥阀段电压绝对值不超过N_FV_cmax。该阶段桥臂电流流经MOV回路。

5）t₄—t₅：t₄时刻开始，全桥阀段电压的绝对值开始下降，t₅时刻全桥阀段电压下降至0，气隙的绝缘恢复。该阶段桥臂电流逐渐转移至全桥阀段。

桥臂电流的流通路径如图 7所示。由图可知，当全桥阀段电压达到MOV残压时，即t₃时刻，故障电流流经MOV回路，消耗了故障能量，减小了对MMC中FBSM电容的充电时间，因此采用此辅助耗能装置可以有效地限制过电压。

图  7  桥臂电流流通路径

Figure  7.  Flow path of arm current

下载: 全尺寸图片 幻灯片

4.   辅助耗能装置参数设计

辅助耗能装置需要确保子模块不过压闭锁，因此需要选择适当的MOV与气隙参数。

4.1   MOV参数的选取

子模块中存在杂散电感，其过电压峰值将会高于制造商提供的V_RES，因此在考虑MOV的残压时，要留有一定的裕度，即：

式中μ为裕度系数，μ < 1。

在MOV回路中串联气隙后，其残压比α'将不再受到MOV固有残压比α的限制，α'可以小于α。若规定V'_REF为气隙与MOV串联回路的1 mA电流下的参考电压，V_REF为MOV固有的1 mA电流下的参考电压，则：

式中ε %为子模块电容电压波动率，一般取5%~15%。

为确保MOV的可靠动作，其长期工作电压V_mov的选择通常要考虑一定的裕度。V_mov的确定方法如下：

式中β与系统电压有关，一般取1.05~1.1。

4.2   气隙参数的选取

为改善MOV的非线性特性，稳态时气隙与MOV共同分压，如式(23)所示；故障后气隙两端电压达到击穿电压之后首先被击穿，仅有MOV投入。

规定V_gpb为气隙的击穿电压，其波动率不超过10%^[21]。在选择气隙击穿电压时可以从两方面进行考虑：1）气隙在器件过压之前击穿，及时投入MOV进行耗能；2）稳态时避免气隙发生击穿，否则周期性的击穿会影响气隙的工作寿命。气隙击穿电压V_gpb的确定如式(24)表示。

式中：R₁、R₂分别为MOV与气隙的并联电阻；V'_REF为气隙与MOV串联回路的1 mA电流下的参考电压；η %为气隙击穿电压的波动率；V_qmax为全桥阀段的全桥子模块全部负向投入时所要求的的负向电压最大值。

5.   仿真验证

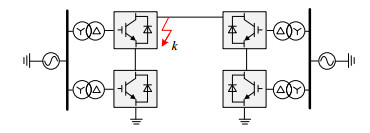
为验证本文所提出直流故障穿越方法与子模块过电压抑制策略的有效性，考虑到沙戈荒大规模新能源送出场景，需建立±800 kV/8 000 MW的混合MMC-HVDC系统。考虑到系统的对称性，本文在PSCAD中建立了单极800 kV/4 000 MW的混合MMC-HVDC系统，其示意图如图 8所示。

图  8  MMC系统示意图

Figure  8.  Diagram of MMC system

下载: 全尺寸图片 幻灯片

整流侧与逆变侧均采用半全混合型MMC，全桥子模块占比均为40%。MMC1为整流站，采用定有功功率和定无功功率控制；MMC2为逆变站，采用定直流电压和定无功功率控制。设定系统于2 s时在换流站出口处发生单极接地故障，2.002 s检测到故障，将控制策略切换至直流故障穿越策略。MMC1和MMC2均切换为定子模块电容电压控制和定无功功率控制，故障穿越策略采用模式Ⅲ，其中U_{dc_set}设置为−150 kV。系统详细参数如表 1所示。

表  1  系统参数

Table  1.  Parameters of system

参数	数值		参数	数值
变压器容量/MW	2 200×2		桥臂电抗/mH	22
变压器变比	525/220		全桥比例/%	40
直流电压/kV	800		FBSM个数	73
直流电流/kA	5		HBSM个数	109
有功功率/MW	4 000		子模块电容电压/kV	2.2
无功功率/Mvar	0		子模块容值/mF	29

下载: 导出CSV 

| 显示表格

根据4节的辅助耗能回路的参数设计方法，选择MOV 1 mA电流下的参考电压V_REF为135 kV，残压V_RES为216 kV，气隙击穿电压V_gpb为34 kV，电阻R₁、R₂分别为14.30、3.06 kΩ，电容C₁、C₂分别为0.306、1.430 μF。该组参数下FBSM电压最大值为2.96 kV。

5.1   直流故障清除效果分析

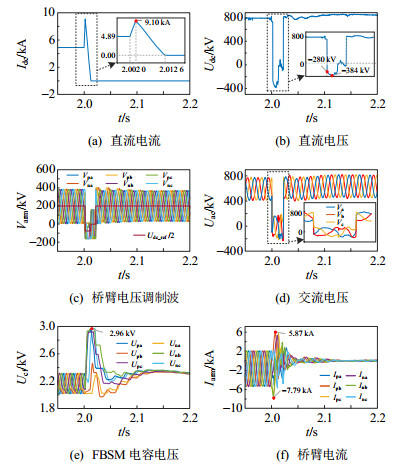
低全桥比例的混合型MMC直流故障穿越过程中整流站波形如图 9所示。

图  9  故障穿越过程中波形

Figure  9.  Waveforms during fault ride-through

下载: 全尺寸图片 幻灯片

图 9(a)、(b)分别为故障穿越过程中系统的直流电流I_dc、直流电压U_dc波形。正常运行工况下，整流站输出的直流电流I_dc稳定在4.89 kA，直流电压稳定在800 kV；故障检测阶段，故障电流快速上升，2.002 s时的故障电流峰值为9.10 kA；检测到故障后(2.002 s)，故障穿越策略被投入，直流电压快速下降至−280 kV，故障电流开始衰减，于故障后12.6 ms衰减至0。由于故障穿越过程中FBSM电容被充电，电容电压上升，因此直流电压峰值低于U_{dc_set}，可以达到−384 kV，有助于加快故障电流的衰减。直流电流衰减至0，直流电压U_dc也自适应恢复至0附近；故障清除后，直流电压U_dc恢复为额定值。

图 9(c)为桥臂电压调制波V_arm波形。正常运行工况下，单个换流阀调制波电压范围为[0, 400] kV；故障发生后的2.0~11.8 ms内，直流电压参考值U_{dc_ref}为−150 kV，调制波电压下限−N_FU_cn为−160 kV，上限为10 kV，调制波电压范围为[−160, 10] kV；故障发生后的12.0~22.0 ms内，U_{dc_ref}自适应变化为0，调制波电压范围为[−160, 160] kV；2.022 s后，调制波电压范围恢复至[0, 400] kV。图 9(d)为阀侧交流电压V_ac波形，故障穿越期间由于桥臂电压调制波的交流分量被限幅，因此故障穿越期间的阀侧交流电压波形略有畸变。

图 9(e)为FBSM电容电压U_cf波形。正常运行工况下，子模块电容电压U_cn为2.2 kV，其波动率为7.5%；故障穿越策略投入后，FBSM电容电压上升，其中b相下桥臂FBSM电容电压上升幅值最大，为2.96 kV，未超越3.1 kV，子模块不会过压闭锁。图 9(f)为桥臂电流I_arm波形，其绝对值最大为7.79 kA，该系统采用额定电流5 kA的IGBT，短时过流能力可以达到8.5 kA，不会导致子模块闭锁。

5.2   全桥子模块过电压抑制效果分析

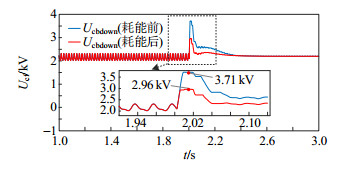
选择过电压程度最高的1个桥臂(b相下桥臂)，验证子模块过电压抑制策略的有效性。添加辅助耗能设备前后的FBSM电容电压及其局部波形如图 10所示。

图  10  过电压抑制前后FBSM电容电压波形

Figure  10.  FBSM voltage waveforms before and after overvoltage suppression

下载: 全尺寸图片 幻灯片

在投入子模块电容电压抑制措施之前，FBSM电容电压最高达到3.71 kV，超越了3.1 kV，导致子模块闭锁；投入子模块电容电压抑制措施，其电压最大值V_cmax = 2.96 kV，与MOV残压选择值对应。由图 10可知，投入子模块电容电压抑制措施可以解决全桥比例降低后的FBSM过压问题。

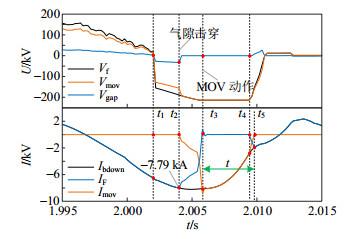
辅助耗能装置动作过程中各波形如图 11所示。t₁时刻前，气隙不会被击穿，辅助耗能装置不会影响桥臂的正常工作。t₁—t₂时段故障穿越策略被投入，全桥子模块输出负压，V_f、V_mov、V_gap均反向增大，该时段气隙尚未达到其击穿电压，未被击穿；MOV回路电流I_mov为0，t₂时刻I_F达到负向最大，为−7.79 kA；t₂—t₃时段气隙两端电压达到其击穿电压，气隙被击穿；MOV的等效电阻逐渐减小，桥臂电流逐渐转移至MOV回路。t₃—t₄时段MOV持续耗能，桥臂电流全部流经MOV回路。t₄—t₅时段桥臂电流逐渐转移至全桥阀段，t₅时刻气隙绝缘恢复，桥臂电流再次流经全桥阀段。并联辅助耗能装置可以在t₃—t₅时段显著降低桥臂电流对全桥子模块的充电时间，其总时长Δt为4 ms，有利于降低全桥子模块电容的电压上升幅值。

图  11  耗能后桥臂电压、电流波形

Figure  11.  The waveforms of the arm voltage and current after the energy dissipation device is put into operation

下载: 全尺寸图片 幻灯片

5.3   故障清除方案对比

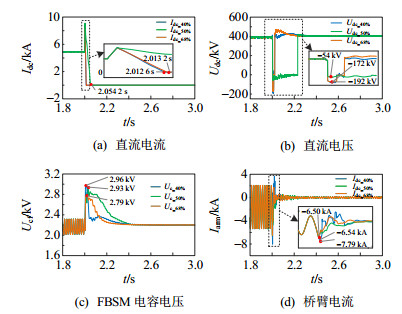
40%全桥比例混合型MMC中FBSM个数为73，HBSM个数为109，U_{dc_set}为−150 kV。根据式(4)，若选择传统故障穿越模式Ⅱ，且具备同样的故障穿越能力，需FBSM个数125，HBSM个数57，全桥占比为68%。为验证本文所提方案相较传统方案的优越性，分别搭建40%、50%、68% 3种全桥比例下的混合MMC仿真模型，分别定义为方案1、2和3。除FBSM、HBSM个数不同外，三方案其余主电路参数均一致，如表 1所示。其中方案1采用本文所提故障穿越模式Ⅲ，方案2、3均采用传统故障穿越模式Ⅱ。3种方案故障穿越过程中各波形对比如图 12所示。

图  12  方案对比波形

Figure  12.  Scheme comparison waveforms

下载: 全尺寸图片 幻灯片

图 12(a)为直流故障穿越期间直流电流I_dc波形，其中方案1—3中故障电流衰减至0的时间分别为故障发生后12.6、54.2、13.2 ms，由图可知，采用方案1(40%)直流故障电流衰减最快，方案3(68%)次之，方案2(50%)最慢。图 12(b)为直流故障穿越期间直流电压U_dc波形(单阀)，方案1—3中负压最小值分别为−192、−54、−172 kV，方案1 (40%)的负直流电压生成能力略高于方案3(68%)。图 12(c)为故障穿越期间FBSM电容电压U_cf波形，方案1—3中FBSM电容电压最大值分别为2.96、2.93、2.79 kV，均未超越3.1 kV。分析图 12(a)—(c)可知：

1）全桥比例40%与50%比较：全桥占比50%是传统认知中的最低比例。相较方案2(50%)，方案1(40%)的故障清除时间减小了41.6 ms，其故障清除速度提升了76.8%。

2）全桥比例40%与68%比较：方案1(40%)与方案3(68%)故障清除能力相近，但方案1中FBSM的过电压程度要高于方案3(过电压允许范围内)，因此直流侧负压相对较低，直流故障清除速度稍快。此外，方案1相较于方案3节省了41.2%的FBSM，经济性提升。

图 12(d)为故障穿越期间桥臂电流I_arm波形，方案1—3中桥臂电流绝对值的最大值分别为7.79、6.54、6.50 kA，其中方案1(40%)中桥臂电流最大，这是因为本文所提方案限制了桥臂电压中交流分量的幅值，因此交流电流幅值增加，进而桥臂电流幅值增加，但仍在规定范围内。

综上所述，本文所提故障穿越方案与子模块过电压抑制策略，可以在满足混合MMC直流故障穿越需求的同时降低FBSM占比，提升其经济性。

6.   结论

本文提出一种低全桥比例混合MMC的直流故障穿越方法及过电压抑制策略，具体结论如下：

1）提出了一种协同调制波自适应限幅的改进定直流电流控制，桥臂电压自适应限幅环节与负直流电压生成环节协同配合，将桥臂电压调制波由正弦波变为平顶波，短时削弱了混合型MMC对交流侧的电压支撑能力，提升了低全桥比例混合型MMC的负直流电压生成能力；

2）为防止负投入的FBSM被过度充电，提出了一种子模块过电压抑制策略，通过MOV与气隙串联调制MOV的非线性特性，进而实现了FBSM过压的适配保护；

3）与传统认知中最低比例50%相比较，采用本文所提方案可以在降低FBSM占比的同时，将故障穿越速率提升76.8%；与同等故障穿越能力下的传统方案相比，采用本文所提方案可以减少41.2%的FBSM数量，经济性得到提升。