经DRU-HVDC送出的海上风电场汇集网电气调节特性分析及集群构网控制策略

于浩天; 蔡旭; 杨仁炘; 杨明扬; 汤广福

doi:10.13334/j.0258-8013.pcsee.232795

经DRU-HVDC送出的海上风电场汇集网电气调节特性分析及集群构网控制策略

1.
电力传输与功率变换控制教育部重点实验室(上海交通大学), 上海市闵行区 200240
2.
怀柔实验室, 北京市怀柔区 101499

基金项目:

国家自然科学基金项目 52107201

详细信息

作者简介:
于浩天(1998)，男，博士研究生，研究方向为海上风电低成本送出技术、新能源柔直并网稳定分析与控制，yht56114@sjtu.edu.cn

蔡旭(1964)，男，博士，教授，博士生导师，研究方向为可再生能源功率变换与并网技术、大功率电力电子与电力系统控制等

杨明扬(1994)，男，博士，研究方向为海上风电轻型直流输电，1798284716@qq.com

汤广福(1966)，男，博士，中国工程院院士，研究方向为电力系统大功率电力电子技术等

通讯作者:
杨仁炘(1992)，男，博士，助理研究员，研究方向为柔性直流输电技术及可再生能源友好并网技术，frank_yang@sjtu.edu.cn

中图分类号: TM614
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2023-12-21
- 发布日期: 2024-07-07
- 刊出日期: 2025-03-19

Analysis of Electrical Regulation Characteristics and Group Grid-forming Control Strategy of DRU-HVDC Integrated Offshore Wind Farm

1.
Key Laboratory of Control of Power Transmission and Conversion (Shanghai Jiao Tong University), Ministry of Education, Minhang District, Shanghai 200240, China
2.
Huairou Laboratory, Huairou District, Beijing 101499, China

Funds:

National Natural Science Foundation of China 52107201

摘要

摘要: 基于构网型风电场与二极管不控整流单元(diode rectifier unit，DRU)的低成本直流送出方案是目前大规模远海风电开发的热点问题。风电机组的构网控制策略是该送出方案的关键，针对现有风机构网策略控制率设计原理不完善、控制结构改造难度大、缺乏同步机理分析等问题，提出使用电压/功率因数节点来刻画DRU的基频功率特性，并利用BP-神经网络实现考虑换流特性及多重化后的DRU节点特性拟合。在此基础上，通过节点-潮流关系揭示风电汇集网络的等效负荷特性、电压/频率构建机理和对风电机组控制率设计的要求。进而提出一种基于锁相环与频率-无功下垂实现自同步的机组网侧变换器集群构网控制策略，完善下垂增益的设计和机组间的同步机理，并采用阻抗法分析验证所提控制策略在系统不同工况的宽频交互稳定性。最后，通过PSCAD/EMTDC仿真验证分析建模的准确性和构网控制策略的有效性。
- 海上风电 /
- 二极管不控整流单元 /
- 电压/功率因数节点 /
- 构网控制 /
- 宽频交互稳定性
Abstract: The low-cost high voltage direct current (HVDC) transmission scheme based on diode rectifier unit (DRU) and grid-forming (GFM) offshore wind farms (OWFs) is a hot topic in the development of large-scale distant offshore wind power. The GFM control strategy of wind turbines is the critical point of this scheme. However, there are still challenges, including the incomplete control law design mechanism, the difficulties in modifying the control structure, and the lack of synchronization mechanism analysis. To solve these problems, the voltage/power factor (U/PF) node model is proposed in this paper to describe the fundamental-frequency power characteristics of the DRU, and the backpropagation (BP) neural network method is utilized to fit the commutation process and multi-pulse topology features. Based on the equivalent load characteristics of the offshore AC system, the mechanism for the voltage/frequency formation, and the control law design requirements of wind turbines are revealed through the node-power flow relation. Furthermore, a clustered GFM control strategy is proposed for grid-side converters of offshore wind turbines based on phase-locked loop (PLL) and frequency-reactive power droop to realize self-synchronization. The design of frequency-reactive droop gain and synchronization mechanism is also elaborated. The wideband interactive stability of the system with the proposed GFM strategy under different operating conditions is analyzed using the impedance method. Finally, simulations are conducted in PSCAD/EMTDC to validate the accuracy of the modeling and analysis, and the effectiveness of the proposed GFM control strategy.
- offshore wind farms (OWFs) /
- diode rectifier unit (DRU) /
- voltage/power factor (U/PF) node /
- grid-forming (GFM) control /
- wideband interactive stability

HTML全文

0. 引言

基于模块化多电平换流器(modular multilevel converter，MMC)的柔性高压直流输电(high voltage direct current，HVDC)技术是目前深远海风电送出的主流方案，但是MMC用于海上换流站时，存在体积重量庞大，建设成本高等问题。采用二极管不控整流单元(diode rectifier unit，DRU)替代MMC能够大幅降低海上换流站的建设成本，近年来成为大容量远海风电直流送出的研究热点^[1-3]。

由于DRU的单向导通及无源特性，如何实现海上风电场(offshore wind farms，OWFs)的黑启动及建立海上交流汇集网的电压与频率是该项技术的一大难点。目前的解决方案包括额外增加一个小容量的辅助换流器，或是由海上风电机组采用构网型控制^[4]来建立电压与频率。后者以其成本和可靠性上的明显优势，是未来深远海风电送出技术的重要发展方向^[5-8]。

近年来，多种用于DRU-HVDC送出的风电机组构网型控制策略被提出，根据同步能力的差异可大致归类为集中通讯方案和分散自同步方案。文献[9-10]提出了基于GPS通讯同步的机组构网控制，该方案仅需改动风电机组网侧变换器的控制策略，易于改造，且不会影响机组载荷，但系统的频率依靠GPS通讯生成，机组间的同步成本高、可靠性差。为解决上述问题，文献[7, 11-13]等提出了基于锁相环(phase locked loop，PLL)的分散式自同步构网控制；文献[5, 14-15]等提出了基于无功-频率下垂环节的分散式自同步构网控制。上述分散式自同步策略能够在无通讯的情况下，实现风电机组间的自同步与无功功率的均分，但均需要将机侧变换器修改为定直流电压控制，会对机组载荷造成不利影响。此外，上述研究大都只对各自所提的构网控制策略进行了分析和验证，而对无功-频率下垂增益的设计依据及机组间的同步机理较少提及，也并未从机理上论述该系统中机组构网控制率的设计依据。

由于DRU的不控整流特性，风电场汇集网的电压、频率与有功、无功功率之间的等效负荷特性与传统电网差别较大，厘清上述关系是构建机组构网控制率，实现系统源荷匹配的关键之一。文献[11-12]通过仿真外特性展示了风电场汇集网电压、频率变化对系统传输有功、无功功率的影响；文献[14]则通过仿真外特性的数值灵敏度对上述影响进行了量化分析；文献[16-18]进一步建立了风电机组输出的电压幅值/频率与其跟PCC点间的有功/无功传输解析关系，但对DRU基频功率传输特性的建模分析仍有待完善；文献[19]对上述问题进行了完善，但对DRU基频功率特性的建模基于DRU接直流电流源、交流电压源的前提假设，与实际系统存在差异；文献[20]考虑DRU直流电压对交流电压的钳位作用后，建立了其基频功率传输特性模型，但建模未涉及DRU电流换相及多重化拓扑，模型精度有待商榷。

综上，在海上风电经DRU-HVDC并网系统中，现有研究在DRU的精确建模和风电场汇集网等效负荷特性分析上存在不足，在机组构网控制率和关键构网控制参数的设计及机组间同步机理分析方面有待深入研究。为解决上述问题，本文主要从以下几个方面展开研究工作：

1）提出更为精确的电压幅值/功率因数(voltage/power factor，U/PF)节点模型，用于刻画DRU交流侧基频功率传输特性。该节点模型通过BP-神经网络^[21]方法建模，可用于含DRU的海上风电场的潮流分析，为大规模海上风电经DRU-HVDC送出系统的控制率设计提供协助；

2）基于所建立的DRU节点模型，从系统功率平衡角度提出机组构网控制率的设计机理，进而提出一种风电机组的网侧变换器集群构网控制策略，并从系统频率平衡点存在和稳定角度给出频率-无功下垂系数的设计方法；

3）诠释机组间的无功自同步机理。通过类比同步机的摇摆方程，结合机组滤波电容、无功下垂及锁相环控制动态，建立机组间的无功-功角动态方程，明确锁相环及无功-频率下垂参数在实现机组间同步的作用。

最后，本文采用阻抗法分析所提控制策略下海上交流系统在不同工况下的宽频交互稳定性，并通过PSCAD/EMTDC仿真验证所建DRU的U/PF节点模型、系统节点-潮流关系的准确性以及所提构网控制策略在海上风电场黑启动、稳态运行以及故障穿越方面的有效性。

1. 海上风电场经DRU-HVDC送出系统拓扑

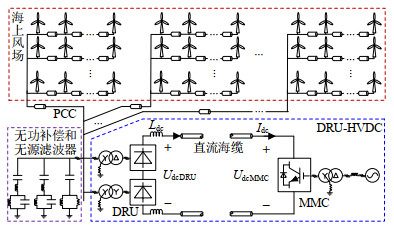
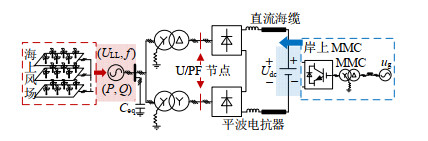
海上风场经DRU-HVDC送出系统的拓扑如图 1所示。其中海上风电场采用中压汇集以节省海上升压变压器，无功补偿和无源滤波器用来补偿DRU的无功消耗和改善海上电网的电能质量，DRU-HVDC直流侧配备平波电抗器以降低高压直流系统电流谐波，受端MMC采用定直流电压控制以建立HVDC系统的直流电压。由于DRU的无源特性，海上风电机组需要采用构网控制以建立海上风场的电网电压和频率。

图 1 海上风电场经DRU-HVDC送出并网系统

Figure 1. The DRU-HVDC integrated OWFs

下载: 全尺寸图片幻灯片

2. 经DRU-HVDC送出的风电场运行特性分析

尽管现有研究已提出诸多风电机组的构网控制策略用于海上风场经DRU-HVDC送出并网，但构网控制策略的设计依据—海上风场经DRU-HVDC送出系统的运行机理仍不完善。故本节首先建立DRU的U/PF节点模型以便于刻画海上风电汇集网包含DRU-HVDC的负荷特性，进一步地从系统源、荷匹配的角度完善海上风电经DRU-HVDC送出系统的运行机理。

2.1 DRU交流端口的U/PF节点特性建模

DRU作为一种被动开关元件，其开关函数由外部系统决定。定义DRU交流端口为U/PF节点，U为相交流电压幅值，PF为功率因数(power factor)。

以六脉波DRU的U/PF节点模型为例，忽略换流，交流侧接电压源，直流侧接电流源，其交流端口的U/PF节点模型为 $U = {\pi }{U_{{\text{dc}}}}/(3\sqrt 3 )$ ，cosφ = 1，体现为交流电压对直流电压的钳位^[19]。而在其交流侧接电流源，直流侧接电压源，持续换流，其交流端口的U/PF节点模型为U = 2U_dc/π，cosφ = 1，体现为直流电压对交流电压的钳位，较为接近图 1系统特性。

但在考虑DRU的换流和多重化特性后，其导通特性更加复杂^[22]在DRU直交流侧均接电压源工况下，文献[23]通过时域分段线性化分析方法得出DRU开关特性取决于直/交流侧电压比和系统频率。故可通过BP-神经网络^[21]对考虑换流和多重化的DRU进行U/PF节点建模。

使用BP-神经网络方法，以DRU直/交流侧电源电压比和系统频率为输入变量，DRU的U/PF节点模型可表示为

$\left\{ \begin{array}{l} U = {F_1}(m, \omega ) \hfill \\ {\text{cos}}\varphi = {F_2}(m, \omega ) \hfill \\ m = \frac{{{U_{{\text{dc}}}}}}{{{U_{{\text{LL}}}}}} \hfill \\ \end{array} \right.$

(1)

式中：U为DRU交流端口的电压；cosφ为DRU交流端口的功率因数；m为直/交流侧电压的比值，U_dc为DRU直流侧电压；U_LL为交流电压源线电压幅值；F₁、F₂为非线性函数映射。

对F₁、F₂的BP-神经网络建模过程如下：

1）数据的获取：DRU直/交流侧电压比和频率作为其交流端口输出电压幅值和功率因数的自变量，故需要测量DRU在不同(m, ω)下对应的(U, cosφ)；并且，为保证训练模型的泛化能力，训练集、验证集、测试集均应涵盖系统的正常运行范围，故数据集中的m应涵盖系统传输功率在0~1 pu的工况，同时ω应涵盖49.5~50.5 Hz；此外，训练集、验证集、测试集的数据量大致保持8 : 1 : 1。

2）神经网络的优化与训练：由于本文模型的输入/输出变量少、映射关系明确，故BP神经网络的隐藏层数N₁和隐藏层神经元个数N_2k (k = 1, 2, ⋯, N₁)相对较少；在给定N₁和N_2k上限的条件下，以训练集数据训练所有N₁和N_2k组合下的神经网络模型，并在验证集参数下以方差最小优化N₁和N_2k。

3）准确性及泛化能力验证：神经网络输出与验证集的拟合程度定义为准确性δ，与测试集的拟合程度定义为泛化能力η，δ与η可表示为

$\left\{ \begin{array}{l} \delta = \frac{1}{N}\frac{{\sum\limits_{h = 1}^N {{{({{\hat y}_h} - {y_h})}^2}} }}{{y_n^2}} \hfill \\ \eta = 1 - \frac{{\sum\limits_{h = 1}^N {{{({{\hat y}_h} - {y_h})}^2}} }}{{\sum\limits_{h = 1}^N {{{({y_h} - \bar y)}^2}} }} \hfill \\ \end{array} \right.$

(2)

式中：y_h为验证集或测试集测量数据；y_n为数据的额定值；N为验证集和测试集的数据量；符号“ˆ”表示神经网络的输出；符号“ˉ”表示测量数据的平均值。该建模方法的验证于4节给出。

2.2 风电场汇集网运行特性分析

2.2.1 风电场汇集网的等效负荷特性

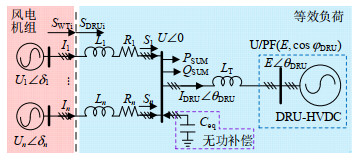
基于所建DRU的U/PF节点模型，E、cosφ_DRU视为已知条件；并结合图 2所示的海上风电等值系统，进一步对风电场汇集网运行特性进行分析。图中将海上风电汇集网分为了风电机组部分和等效负荷部分，风电机组具备固有的有功、无功输出特性S_WTi，其由机组控制决定；而S_DRUi由系统节点-潮流方程推导得到，故定义为系统等效负荷特性。

图 2 海上风电场汇集网等值系统

Figure 2. The equivalent system of offshore ac grid

下载: 全尺寸图片幻灯片

首先对系统等效负荷特性进行分析，在海上风场传输功率P_SUM确定条件下，P_SUM、Q_SUM与风电场PCC点电压幅值U间的解析关系可表示为

$\left\{ \begin{array}{l} {P_{{\text{SUM}}}} \approx \frac{1}{{{\omega _0}{L_{\text{T}}}}}E\cos {\varphi _{{\text{DRU}}}}[\sqrt {{U^2} - {{(E\cos {\varphi _{{\text{DRU}}}})}^2}} - \hfill \\ \quad E\sin {\varphi _{{\text{DRU}}}}](1 - \frac{{{\omega _{\text{r}}}}}{{{\omega _0}}}) \hfill \\ {Q_{{\text{SUM}}}} \approx - {\text{j}}{\omega _0}{C_{{\text{eq}}}}{U^2}(1 + \frac{{{\omega _{\text{r}}}}}{{{\omega _0}}}) + {\text{j}}\frac{{{U^2} - {E^2}{{\cos }^2}{\varphi _{{\text{DRU}}}}}}{{{\omega _0}{L_{\text{T}}}}} \cdot \hfill \\ \quad (1 - \frac{{{\omega _{\text{r}}}}}{{{\omega _0}}}) - {\text{j}}\frac{{E\sin {\varphi _{{\text{DRU}}}}\sqrt {{U^2} - {{(E\cos {\varphi _{{\text{DRU}}}})}^2}} }}{{{\omega _0}{L_{\text{T}}}}}(1 - \frac{{{\omega _{\text{r}}}}}{{{\omega _0}}}) \hfill \\ \end{array} \right.$

(3)

式中：ω为系统运行频率，ω = ω_r + ω₀，| ω_r /ω₀ | < 1%可视为小量o(1)并忽略；L_T为整流变漏抗；C_eq为无源滤波器基频等值电容，故U、Q_SUM可近似视为由P_SUM唯一确定。

进而，风电机组有功、无功输出功率可记作：

$\left\{ \begin{array}{l} {P_{{\text{DRU}}i}} = {U_i}\cos {\varphi _i}[{U_i}\cos ({\theta _i} - {\varphi _i}) - \hfill \\ \quad \quad \sqrt {{U^2} - {{\sin }^2}({\theta _i} - {\varphi _i})U_i^2} ]/ \hfill \\ \quad \quad \sqrt {R_i^2 + \omega _0^2L_i^2(1 + \frac{{2{\omega _{\text{r}}}}}{{{\omega _0}}})} = {f_{{\text{DRU}}i}}({U_i}, \omega ) \hfill \\ {Q_{{\text{DRU}}i}} = {U_i}\sin {\varphi _i}[{U_i}\cos ({\theta _i} - {\varphi _i}) - \hfill \\ \quad \quad \sqrt {{U^2} - {{\sin }^2}({\theta _i} - {\varphi _i})U_i^2} ]/ \hfill \\ \quad \quad \sqrt {R_i^2 + \omega _0^2L_i^2(1 + \frac{{2{\omega _{\text{r}}}}}{{{\omega _0}}})} = {g_{{\text{DRU}}i}}({U_i}, \omega ) \hfill \\ \end{array} \right.$

(4)

式中：下标i为机组编号；R_i、L_i和θ_i为机组i馈线的电阻、电感和阻抗角；φ_i、U_i为机组i的功率因数角和输出电压幅值；定义机组f_DRUi、g_DRUi为机组i节点的等值负荷特性。

与式(3)同理，机组i的等值负荷特性同样可忽略频率变化的影响，近似视为交流电压的单值函数，即：

$\left\{ \begin{array}{l} {P_{{\text{DRU}}i}} = {f_{{\text{DRU}}i}}({U_i}, \omega ) \approx {f_{{\text{DRU}}i}}({U_i}) \hfill \\ {Q_{{\text{DRU}}i}} = {g_{{\text{DRU}}i}}({U_i}, \omega ) \approx {g_{{\text{DRU}}i}}({U_i}) \hfill \\ \end{array} \right.$

(5)

故U_i、P_DRUi和Q_DRUi三者同调。

同时，机组i与PCC点电压之间的功角δ_i满足：

$\frac{{{U_i}}}{{\sin ({\delta _i} + {\theta _i} - {\varphi _i})}} = \frac{U}{{\sin ({\theta _i} - {\varphi _i})}}$

(6)

故U_i和U相量间的功角无法独立调节，功角会随U_i的增大而增大。故包含DRU-HVDC在内的风电汇集网络具有一定的无源负荷特性，即电压确定，负荷传输有功、无功确定。

之后对风电汇集网络(U_i, ω)平衡点构建过程进行阐述，以说明风电机组应具备的功率特性。

2.2.2 风电场汇集网的电压/频率构建机理

除上述负荷特性外，从功率平衡的角度，风电汇集网还需使其等效负荷部分具备有功平衡节点性质，使风电机组部分的发出功率均可被送出。而由于等效负荷部分不可控，为使其成为有功平衡节点，需要通过风电机组部分的控制进行配合。而根据风电汇集网等效负荷部分的固有有功特性，如式(5)，说明了风电汇集网等效负荷的消耗有功仅与机组输出电压幅值相关，故机组仅需根据发电功率通过PI控制灵活调节输出电压幅值，即可使风电汇集网的负荷部分具备有功平衡节点性质。

故在机组发电功率P_WTi确定的条件下，根据系统的有功平衡：

${P_{{\text{WT}}i}} = {P_{{\text{DRU}}i}} = {f_{{\text{DRU}}i}}({U_i})$

(7)

则可确定机组i的输出电压U_i，进而可通过式(5) g_DRUi(U_i)可确定等效负荷无功Q_DRUi。

而在该系统中，海上风电场作为源，应具备无功平衡节点能力，以维持系统的稳定运行，故通过系统的无功平衡：

${Q_{{\text{WT}}i}} = {g_{{\text{WT}}i}}({U_i}, \omega ) = {Q_{{\text{DRU}}i}} = {g_{{\text{DRU}}i}}({U_i})$

(8)

由机组无功输出特性g_WTi(U_i, ω)可确定系统频率。

2.2.3 风电机组控制率的设计要求

虽然等效负荷具有极强的功率耦合特性，即f_DRUi(U_i)和Q_DRUi(U_i)，风电机组的控制仍应尽量保证输出功率特性解耦；此外，为确定系统频率，风电机组需具备ω-Q特性；故风电机组的输出无功特性g_WTi(U_i, ω)可设计为g_WTi(ω)。

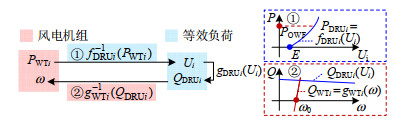
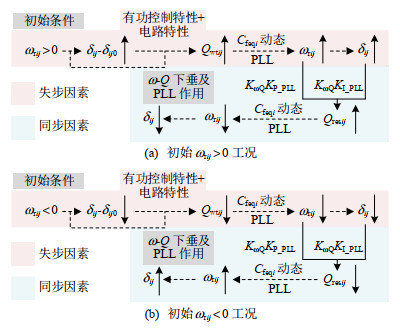
此时，风电汇集网络(U_i, ω)平衡点构建过程可表示为图 3，其右侧①表示系统源-荷有功平衡以确定系统电压平衡点；②表示系统源-荷无功平衡以确定系统频率平衡点，蓝色线段代表汇集网等效负荷特性、红色线条代表风电机组特性，其中变量含义与图 2相同。机组输出有功、无功输出函数f_DRUi和g_DRUi均来自式(4)，因为ω变化范围小，故g_DRUi近似为直线，斜率由ω₀处斜率近似，机组的ω-Q特性需具备较大斜率以保证ω平衡点处于(1 ± 0.01)pu以内。

图 3 系统的电压/频率平衡点构建机理

Figure 3. The principle for constructing the system voltage/frequency equilibrium point

下载: 全尺寸图片幻灯片

故对于该系统的构网，平衡节点平衡的有功或无功功率应与系统尚未确定的电压幅值或频率之间具备固有的或通过控制构造的强映射关系。该强映射关系是指平衡节点平衡的有功或无功功率对电压幅值或频率的变化敏感性强。风电汇集网的负荷部分具备固有的有功功率-电压幅值强映射关系，在机组控制的配合下可作为有功平衡节点，通过有功平衡构建系统电压幅值；风电汇集网的风电机组部分通过控制构造了的无功功率-频率强映射关系，其可作为无功平衡节点，通过无功平衡构建系统频率。

3. 一种海上风电变流器集群构网控制策略

3.1 风电机组构网控制策略设计

根据2节的分析，为满足DRU-HVDC系统的送出需求，风电机组需要通过控制构建P_WTi-U_i和ω-Q_WTi外特性。且P_WTi和ω为控制量，U_i和Q_WTi为被控量。

在机组P_WTi的控制环节设计方面：一方面，考到机侧变换器控制机组直流母线电压存在加剧发电机转矩脉动^[24]、影响发电机MPPT运行^[25]、加剧机网侧系统耦合^[26]以及对现有风电机组主控需要大规模改动等弊端，故需保持机侧变换器进行MPPT等发电机转速控制，网侧变换器进行直流电压控制的架构；另一方面，需要保证经功率环输出的 ${U_{i{\text{wt}}}} = f_{{\text{WT}}}^{i - 1}({P_{{\text{ref}}}})$ 与等效负荷特性对应的U_iDRU = $f_{{\text{DRU}}}^{i - 1}({P_{{\text{ref}}}})$ ，两者相等，即U_iwt = U_iDRU。故网侧变换器的d轴外环采用定直流电压控制，使用PI控制器输出交流电压幅值参考。

在机组ω的控制环节设计方面：首先，需保证机组间的同步不依赖通讯；其次，考虑到系统频率的越限会对海上风电系统中电力设备的安全运行、系统的电能质量以及系统运行的经济性等方面造成不利影响，故按国标，机组输出频率需始终处于1 ± 0.01 pu以内^[27]；此外，计及机组作为系统的无功平衡节点且DRU额定运行条件下的无功消耗较大，故需保证机组无功补偿的均分，以避免机组过载。故网侧变换器采用PLL和ω-Q下垂构成同步控制，其同步机理于3.2节中详细给出；由于频率是全局量，故为机组设置相同的大ω-Q下垂增益即可满足上述要求。

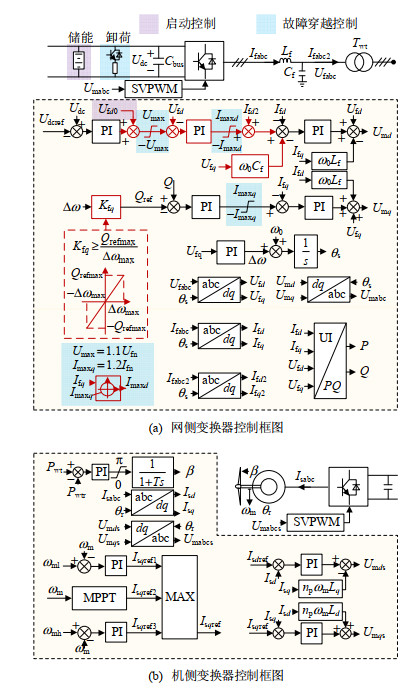
综合上述控制环节的设计，本文提出了海上风电变流器集群构网控制结构如图 4所示。其中，部分机组配置直流储能，容量为机组的3%~5%，用于海上风电场的黑启动。

图 4 一种基于PLL与ω-Q下垂同步的机组集群构网控制

Figure 4. The PLL and ω-Q droop-synchronized group GFM control of WTs

下载: 全尺寸图片幻灯片

在机组网侧变换器部分：L_f为网侧变换器的滤波电感；I_f为流过L_f的三相电流；C_f为网侧变换器的滤波电容，储能用于海上风场的黑启动，卸荷用于海上风场的故障穿越；U_f为C_f上的对地三相电压；T_wt为风电机组的箱变；I_wt为流过T_wt低压侧的三相电流；C_bus为风电机组的直流母线；U_dc为C_bus上的直流电压；U_m为机组的三相调制电压；U_fx(x = d, q)为U_f的dq轴分量，I_fx为I_f的dq轴分量，I_wtx为I_wt的dq轴分量，U_mx为U_m的dq轴分量；I_fn为I_f的额定幅值；U_fn为U_f的额定幅值；ω₀为风电机组的额定频率；ω_r为频率偏差；Q为机组变换器的无功输出；Q_ref为其参考值；K_ωQ为ω-Q下垂增益；K_cf为电流前馈增益设置为0.8；Q_refmax为机组输出无功功率上限；ω_rmax为最大允许频率波动。

在机组机侧变换器部分：I_s为定子电流；ω_m为同步机角频率；θ_r为同步机相角；β为桨距角；U_mr为机侧变换器的三相调制电压；I_sx(x = d, q)为I_s的dq轴分量，U_mrx为U_mr的dq轴分量；P_wtr为同步机额定功率；P_wt为同步机输出功率；ω_ml为低恒转速参考值；ω_mh为恒额定转速参考值；n_p为极对数；L_d和L_q分别为dq轴电枢电感。

进一步地，对机组ω-Q下垂增益的设计和机组间的同步机理进行如下补充。

3.2 ω-Q下垂增益的设计原则

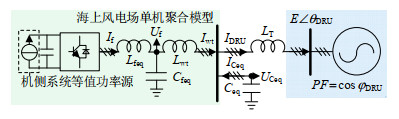
为进一步阐明风电机组ω-Q下垂控制的合理性，本节从ω-Q下垂控制存在系统平衡点且平衡点稳定两方面给出其增益的设计依据。首先忽略海上变流群体间的差异，将海上风场以单机聚合模型等效，等值系统如图 5所示。其中：所有参数都已归算到同一电压等级，DRU用U/PF节点模型表示，L_T为整流变漏抗；C_eq为无源滤波及无功补偿基频等值电容；L_feq、C_feq为机组等值LC滤波器；L_wteq为机组箱变等值漏抗，机侧系统不参与ω-Q下垂控制故以恒功率源等效。

图 5 风电场单机聚合经DRU-HVDC送出系统

Figure 5. DRU-HVDC integrated single-wind turbine aggregated OWF system

下载: 全尺寸图片幻灯片

首先，给出系统平衡点存在条件对机组ω-Q下垂增益设计的约束。系统运行无功消耗可表示为

$\begin{array}{l} {Q_{{\text{load}}}} = \omega ({L_{{\text{wteq}}}}I_{{\text{wteq}}}^2 + {L_{\text{T}}}I_{{\text{DRU}}}^2 - {C_{{\text{eq}}}}U_{{\text{Ceq}}}^2 - \hfill \\ \quad \quad {C_{{\text{feq}}}}U_{{\text{feq}}}^2) = {K_{{\text{load}}}}\omega \hfill \\ \end{array}$

(9)

式中ω为系统频率，其他变量含义如图 5所示，海上风场聚合风电机组的无功输出Q_c可表示为

${Q_{\text{c}}} = {K_{\mathtt{ω}{\text{Q}}}}{\omega _{\text{r}}}$

(10)

式中：K_ωQ为ω-Q下垂增益；ω_r为相对角频率；ω、ω_r的关系如式(3)所示。

故系统频率平衡点可表示为

$\left\{ \begin{array}{l} {\omega _{\text{r}}} = \frac{{{K_{{\text{load}}}}}}{{{K_{\mathtt{ω}{\text{Q}}}} - {K_{{\text{load}}}}}}{\omega _0} \hfill \\ \omega = \frac{{{K_{\mathtt{ω}{\text{Q}}}}}}{{{K_{\mathtt{ω}{\text{Q}}}} - {K_{load}}}}{\omega _0} \hfill \\ \end{array} \right.$

(11)

考虑到系统允许的ω_r为±0.01 pu，为保证可行域内存在平衡点，故K_ωQ的取值需要相对较大，可表示为

${K_{\mathtt{ω}{\text{Q}}}} > 101{K_{{\text{load}}}} \cup - 99{K_{{\text{load}}}} > {K_{\mathtt{ω}{\text{Q}}}}$

(12)

进一步地，给出系统平衡点稳定条件对机组ω-Q下垂控制设计的约束。

在系统平衡点处，系统传输电流和节点电压幅值恒定，式(9)线性化并施加扰动表示为

$\Delta {Q_{{\text{load}}}} = {K_{{\text{load}}}}\Delta \omega + \Delta {Q_{{\text{dis}}}}$

(13)

结合机端滤波电容动态：

$\left\{ \begin{array}{l} s{C_{{\text{feq}}}}\Delta U_{{\text{feq}}q}^{\text{s}} = \Delta I_{{\text{feq}}q}^{\text{s}} - \Delta I_{{\text{wteq}}q}^{\text{s}} - \Delta {\omega _{\text{r}}}{C_{{\text{feq}}}}U_{{\text{feq}}d}^{\text{s}} \hfill \\ \Delta U_{{\text{feq}}q}^{\text{s}} = \frac{2}{{3s{U_{{\text{feq0}}}}{C_{{\text{feq}}}}}}( - \Delta {Q_{\text{c}}} + \Delta {Q_{{\text{load}}}}) \hfill \\ \end{array} \right.$

(14)

式中：“Δ”表示线性化；上标“s”表示电气参考坐标系；U_feq0为等效机组额定输出电压幅值；下标“q”表示q轴分量。

并结合图 4中机组的PLL及ω-Q下垂动态：

$\left\{ \begin{array}{l} \Delta {\omega _{\text{r}}} = s{G_{{\text{PLL}}}}\Delta U_{{\text{feq}}q}^{\text{s}} = {T_{{\text{PLL}}}}\Delta U_{{\text{feq}}q}^{\text{s}} \hfill \\ \Delta {Q_{\text{c}}} = {K_{\mathtt{ω}{\text{Q}}}}\Delta {\omega _{\text{r}}} \hfill \\ \end{array} \right.$

(15)

式中G_PLL为系统PLL的闭环传递函数，其表达式可记为

$\left\{ \begin{array}{l} {G_{{\text{PLL}}}} = \frac{1}{{{U_{{\text{f0}}}}}}\frac{{{\omega _0}({K_{{\text{P}\_\text{PLL}}}}s + {K_{{\text{I}\_\text{PLL}}}})}}{{{s^2} + {\omega _0}({K_{{\text{P}\_\text{PLL}}}}s + {K_{{\text{I}\_\text{PLL}}}})}} \hfill \\ {K_{{\text{P}\_\text{PLL}}}} = 2\xi \frac{{{\omega _{\text{c}}}}}{{{\omega _0}}}\sqrt {\sqrt {{{(2{\xi ^2} + 1)}^2} + 1} - (2{\xi ^2} + 1)} \hfill \\ {K_{{\text{I}\_\text{PLL}}}} = \frac{{\omega _{\text{c}}^2}}{{{\omega _0}}}[\sqrt {{{(2{\xi ^2} + 1)}^2} + 1} - (2{\xi ^2} + 1)] \hfill \\ \end{array} \right.$

(16)

式中：K_{P_PLL}和K_{I_PLL}为标幺化的PLL的PI控制参数；ξ为PLL阻尼比；ω₀为额定角频率；ω_c为PLL截止频率。故G_PLL在带宽内可近似为1，在带宽之外可近似为1/(s/ω_c + 1)，故式(15)中T_PLL的相位在频域上属于[0, π/2]。

联立式(13)—(16)，系统频率动态方程为

$s\Delta {\omega _{\text{r}}} = \frac{{2{T_{{\text{PLL}}}}}}{{3{U_{{\text{f0}}}}{C_{{\text{feq}}}}}}( - {K_{\mathtt{ω}{\text{Q}}}} + {K_{{\text{load}}}})\Delta {\omega _{\text{r}}} + \frac{{2{T_{{\text{PLL}}}}}}{{3{U_{{\text{f0}}}}{C_{{\text{feq}}}}}}\Delta {Q_{{\text{dis}}}}$

(17)

故此时特征根的实部取决于(−K_ωQ + K_load)的正负，当该值为负时，系统特征根为负，平衡点为稳定平衡点，即K_ωQ > K_load。由于K_load的最大值大于0，故为确保平衡点存在且稳定，需要使K_ωQ满足式(12)中的第一个条件，即K_ωQ > 101K_load。

3.3 风电机组的构网控制同步机理

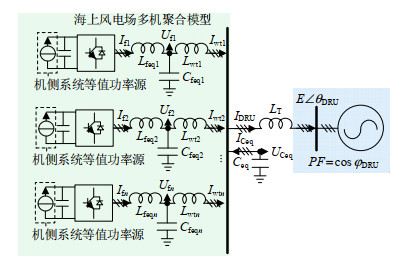
3.2节为说明风电机组ω-Q下垂控制的合理性，将海上风场以单机聚合模型进行了等值。本节则对机组间同步机理做进一步的补充，将海上风场简化为多机聚合模型，如图 6所示。

图 6 风电场多机聚合经DRU-HVDC送出并网系统

Figure 6. DRU-HVDC integrated multi-wind turbine aggregated OWF system

下载: 全尺寸图片幻灯片

基于任意机组的滤波电容动态，在其对应的dq旋转参考坐标系中，q轴电压动态可以表示为

$\left\{ \begin{array}{l} \frac{3}{2}{U_{{\text{f}}id}}{C_{{\text{feq}}i}}\frac{{{\text{d}}{U_{{\text{f}}iq}}}}{{{\text{d}}t}} = - {Q_i} + {Q_{{\text{wt}}i}} \hfill \\ {Q_i} = - \frac{3}{2}{U_{{\text{f}}id}}{I_{{\text{f}}iq}} \hfill \\ {Q_{{\text{wt}}i}} = - \frac{3}{2}{U_{{\text{f}}id}}{I_{{\text{wt}}iq}} \hfill \\ \end{array} \right.$

(18)

式中：变量下标i ∈ (1, 2, ⋯, n)为机组编号；下标“d”、“q”表示dq轴变量，以q轴电流正方向为无功流向；Q_wti为机组滤波电容后端的无功输出；Q_i为机组变换器的无功输出，其他变量含义与上文相同。

结合本文所提ω-Q下垂控制结构，如图 4，因而网侧变换器的无功输出参考Q_refi可表示为

${Q_{{\text{ref}}i}} = {K_{\mathtt{ω}{\text{Q}}}}{\omega _{{\text{r}}i}} + {Q_{i0}}$

(19)

式中：ω_ri为机组PLL的PI输出；K_ωQ为机组的无功-频率下垂系数；Q_i0为机组在额定频率下输出无功参考，图 4中未设置Q_i0，Q_i0可视为0。此外，为简化机组同步动态的分析，忽略无功环闭环动态，近似认为机组无功输出等于其参考值，即Q_i ≈ Q_refi。

因而，联立式(18)、(19)及PLL控制动态，任意一台机组的输出频率动态可表示为

$\begin{array}{l} \frac{{{{\bar U}_{{\text{f}}id}}{{\bar Y}_{{\text{feq}}i}}}}{{{\omega _0}}}\frac{{{\text{d}}{\omega _{{\text{r}}i}}}}{{{\text{d}}t}} = {\omega _0}{{\bar H}_{{\text{PLL}}}}{{\bar Q}_{{\text{wt}}i}} - \hfill \\ \quad \quad {{\bar K}_{\mathtt{ω}{\text{Q}}}}({{\bar K}_{{\text{P}\_\text{PLL}}}}{\omega _{{\text{r}}i}} + {{\bar K}_{{\text{I}\_\text{PLL}}}}{\delta _i}) \hfill \\ \end{array}$

(20)

式中：“ˉ”表示变量的标幺化；Y_feqi = ω₀C_feqi；H_PLL为PLL环的PI控制器；K_{P_PLL}为PLL环的比例增益；K_{I_PLL}为PLL的积分增益；ω₀为系统的额定频率；δ_i为机组变换器输出电压相位相对于PCC电压相位之间的功角。Q_wti由系统潮流关系可表示为

${\bar Q_{{\text{wt}}i}} = - {\bar U_i}{\bar Y_{i{\text{PCC}}}}[{\bar U_i}\sin {\varphi _{i{\text{PCC}}}} + {\bar U_{{\text{PCC}}}}\sin ({\delta _i} - {\varphi _{i{\text{PCC}}}})]$

(21)

式中：Y_iPCC为机组端口和海上风场PCC点之间的联结导纳；φ_iPCC为联接导纳的导纳角；U_PCC为海上风场系统PCC点交流电压幅值。在海上风场内网为感性主导条件下，传输线导纳角φ_iPCC可近似视为−90°(因为机组箱变漏抗远大于线路电阻和分布电容)，同时，由于机组端口与PCC之间的互导纳较大，故额定工况下机组的功角相对较小(δ_i趋近于0)。故式(21)可近似等效为

${\bar Q_{{\text{wt}}i}} \approx ({\bar U_i} - {\bar U_{{\text{PCC}}}}){\bar U_i}{\bar Y_{i{\text{PCC}}}}$

(22)

则进一步地，对于风场的任意两机同步动态可以表示为

$\left\{ \begin{array}{l} \frac{{{\text{d}}{\delta _{ij}}}}{{{\text{d}}t}} = {\omega _{{\text{r}}ij}} \hfill \\ \frac{{{\text{d}}{\omega _{{\text{r}}ij}}}}{{{\text{d}}t}} = \frac{{{\omega _0}}}{{{{\bar U}_{{\text{fd}}i}}{{\bar Y}_{{\text{feq}}i}}}}({\omega _0}{{\bar H}_{{\text{PLL}}}}{{\bar Q}_{{\text{wt}}ij}} - {{\bar Q}_{{\text{res}}ij}}) + {K_\Delta }({{\bar Q}_{{\text{wt}}j}} - {{\bar Q}_j}) \hfill \\ {{\bar Q}_{{\text{wt}}ij}} = {{\bar Q}_{{\text{wt}}i}} - {{\bar Q}_{{\text{wt}}j}} \hfill \\ {{\bar Q}_{{\text{wt}}ij}} = {{\bar K}_{\mathtt{ω}{\text{Q}}}}({{\bar K}_{{\text{P}\_\text{PLL}}}}{\omega _{{\text{r}}ij}} + {{\bar K}_{{\text{I}\_\text{PLL}}}}{\delta _{ij}}) \hfill \\ {K_\Delta } = \frac{{\omega _0^2{{\bar H}_{{\text{PLL}}}}}}{{{{\bar U}_{{\text{fd}}i}}{{\bar Y}_{{\text{feq}}i}}}} - \frac{{\omega _0^2{{\bar H}_{PLL}}}}{{{{\bar U}_{{\text{fd}}j}}{{\bar Y}_{{\text{feq}}j}}}} \approx 0 \hfill \\ \end{array} \right.$

(23)

式中：δ_ij、ω_rij分别为机组i、j之间的功角和相对角频率；K_Δ代表机组电气参数的差异，由于风电机组经设计所得的标幺化参数差异不大，故本文忽略K_Δ的影响。在系统达到稳态，式(23)中的微分项δ_ij、ω_rij为0，并可解得任意两机的功角平衡点δ_ij0和系统频率平衡点ω_ri = ω_rj = ω_r0。可以看出，在本文提出的高增益K_ωQ作用下，机组间将会具有较高的正阻尼和同步转矩，阻尼转矩系数为K_ωQK_{P_PLL}、同步转矩系数为K_ωQK_{I_PLL}，其为机组提供了不依赖通讯的同步能力。

以下基于式(23)所示的机组间同步动态方程和图 7详细说明机组在PLL和ω-Q下垂作用下的同步过程。

图 7 风电机组间的同步过程

Figure 7. The synchronization process among WTGs

下载: 全尺寸图片幻灯片

首先，若两机组间的功角不在平衡点δ_ij0，且ω_rij ≠ 0。如：海上风场处于黑启动阶段或处于机组输出功率变化时。若ω_rij > 0，则会导致机组i相较机组j出力的增加，在有功外环作用下，机组i相较机组j输出电压升高，进而根据式(22)可知，Q_wtij会进一步升高。此时，若无PLL和无功下垂控制，根据式(23)可知ω_rij会进一步升高，导致机组间同步失稳。而若引入PLL和无功下垂控制，则在Q_resij的正阻尼转矩系数和正同步转矩系数作用下，Q_wtij的扰动会受到补偿，迫使ω_rij降低。若ω_rij < 0，则会导致机组i相较机组j出力的减小，在有功外环作用下，机组i相较机组j输出电压降低，进而根据式(22)可知，Q_wtij会进一步降低。此时，PLL和无功下垂控制提供的Q_resij会补偿Q_wtij的扰动，迫使ω_rij升高，最终使ω_rij趋近于0，实现机组间的同步。

4. 仿真验证

4.1 仿真系统

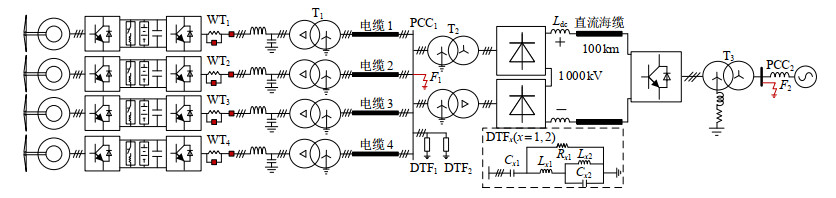
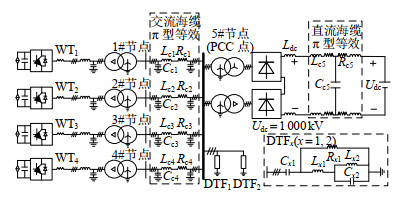
为验证本文所提机组控制策略的有效性，本文基于PSCAD/EMTDC，搭建了海上风场经DRU- HVDC送出系统，如图 8所示。其中海上风场使用多机聚合模型^[28-31]以提高仿真速度，模型的聚合包括两个部分：全功率风电机组的聚合和传输线缆的聚合。全功率风电机组的聚合主要考虑容量、机械参数和电气参数3部分的聚合。聚合容量为所聚合机组的容量和。机械参数部分如风轮机和发电机的惯性时间常数、传动轴的刚性和阻尼系数保持不变，齿轮箱变比和叶片半径的平方与聚合容量同比放大。电气参数部分聚合前后标幺值保持不变。传输线缆的聚合模型采用π型电路，主要考虑对地电容和传输阻抗的聚合。两聚合电容各为详细模型线缆总电容的一半。聚合传输阻抗按视在功率损耗一致计算。该聚合模型与详细风场在动态特性和小扰动频域特性方面的一致性已于文献[30-31]论证，故可用于本文所提变流器集群控制策略的仿真验证。仿真系统额定有功为2 GW，HVDC直流电压±500 kV，详细仿真系统的参数如附录A所示。以下依次给出DRU的U/PF节点建模方法验证，系统潮流分析验证，系统黑启动、稳态运行、及故障穿越的仿真结果。机组故障穿越验证考虑最恶劣工况，包括海上风场PCC点和岸上电网PCC点的三相金属性短路故障。其故障位置已于图 8中标出。风电机组输出三相交流电压限幅1.1 pu，输出三相交流电流限幅1.2 pu。故障穿越期间，系统有功功率由机组的直流卸荷平衡。

图 8 海上风电场经DRU-HVDC送出并网仿真系统

Figure 8. The simulation system of DRU-HVDC integrated OWF

下载: 全尺寸图片幻灯片

4.2 DRU交流端口U/PF节点特性建模方法验证

首先对所提DRU交流端口U/PF节点模型的建模方法进行验证。以图 8系统的等值简化为例，简化后的系统如图 9所示。其中，海上风电场以交流电压源等效，DRU采用通用的12脉波不控整流结构，DRU直流侧保留了其平波电抗器和直流海缆，岸上MMC用直流电压源进行了等效。系统参数如表A2、A3所示。

图 9 海上风电场经12脉DRU-HVDC送出简化系统

Figure 9. The simplified system of 12-pulse DRU-HVDC integrated OWF

下载: 全尺寸图片幻灯片

参照2.1节的步骤，在保持岸上直流电压源电压恒定的情况下，对于训练集数据，改变海上交流电压源输出电压，以DRU起始导通电压0.92 pu至DRU额定导通电压1 pu划分10个等距电压，同时以电源频率49.5~50.5 Hz划分11个等距频率，获取对应的DRU端口电压幅值和功率因数。

对于验证集数据，分别以电压0.925~1.005 pu进行5等距划分，频率取49.75~50.35 Hz进行3等距划分，获取对应的DRU端口电压幅值和功率因数。对于测试集数据，则以电压0.922 5~1.002 5 pu进行5等距划分，频率取49.85~50.45 Hz进行3等距划分获取对应的DRU端口电压幅值和功率因数。

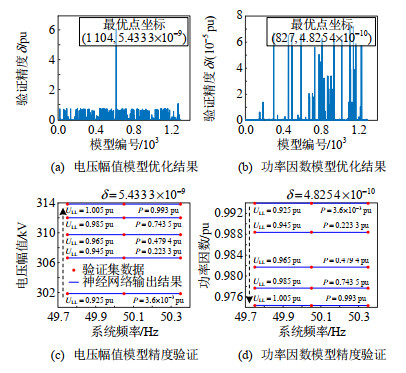
BP-神经网络的训练借助matlab神经网络工具箱完成。神经网络隐藏层数和隐藏层神经元数的确定则借助与验证集的拟合准确性进行优化。本文主要考虑简单结构的神经网络模型，设置隐藏层数上限4，隐藏层神经元数上限5。通过验证集数据对经训练集数据得到的不同结构神经网络模型的拟合准确性δ进行比对，选择δ最小的神经网络结构作为最优结构。BP-神经网络模型的优化结果如图 10所示，其中神经网络模型编号由10进制编号转化为6进制编号即为BP-神经网络结构(转换到6进制时，若出现低位为0而高位不为0，则低位0补1)，如：1104代表隐藏层结构为[5 1 4 1]，827代表隐藏层结构为[3 4 5 5]。

图 10 BP-神经网络的优化及准确性验证

Figure 10. The optimization and accuracy verification of BP-neural network model

下载: 全尺寸图片幻灯片

最后采用结构最优且完成训练的BP-神经网络模型通过测试集数据检验模型的泛化能力，结果如图 11所示。故所建DRU的U/PF节点模型可用于系统的潮流特性分析。

图 11 BP-神经网络模型的泛化能力验证

Figure 11. The validation of the generalization capability of BP-neural network model

下载: 全尺寸图片幻灯片

4.3 海上风电场的功率传输特性验证

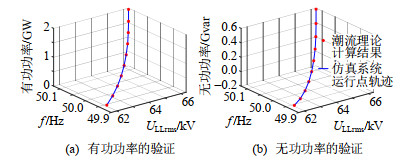
本节给出系统潮流分析的仿真验证结果。基于图 8仿真系统，可得系统全仿真工况的工作点轨迹，如图 12所示。基于2.1节建立的十二脉波DRU交流侧U/PF节点模型，和DRU输入潮流方程，如式(3)，可计算不同海上风场PCC点线电压有效值和系统频率组合下对应DRU的理论有功、无功输入功率。理论计算结果的验证结果如图 12所示，验证了本文建立的DRU交流端口U/PF节点模型和潮流分析的正确性。

图 12 DRU输入有功/无功功率分析仿真验证

Figure 12. The simulation verification for the input active and reactive power analysis of the DRU

下载: 全尺寸图片幻灯片

4.4 海上风电场的黑启动及稳态运行验证

海上风场从黑启动到稳态运行的仿真结果如图 13所示，仿真以岸上MMC完成启动为初始条件。WT₁的直流储能从仿真开始为其直流母线进行充电至额定电压，3 s启动其网侧换流器，建立小于DRU导通阈值的风场初始电压，5 s启动其机侧换流器，开始以额定风速输出功率。进而WT₂、WT₃、WT₄依次于13、28、43 s依次投入，之后于15、30、45 s启动网侧换流器建立机组额定直流母线电压，最终于20、35、50 s启动机侧换流器，以额定风速输出有功功率。在黑启动过程中，机组输出无功功率始终一致，同时电压、电流未出现过压、过流情况。额定工况下电压、电流均处于0.9~1.1 pu以内，海上风场内网稳态频率波动处于0.99~1.01 pu以内。

图 13 海上风场经DRU-HVDC送出系统黑启动至额定运行仿真结果

Figure 13. The simulation results of DRU-HVDC integrated OWF from black start to rated operation condition

下载: 全尺寸图片幻灯片

4.5 海上电网三相短路故障穿越验证

对于海上风场三相短路故障F₁，故障切除时间0.625 s，风电机组额定风速下的故障穿越仿真结果如图 14所示。其中故障穿越及恢复期间，机组输出的电压、电流均保持在限幅以内；机组直流母线卸荷启动来维持机组直流母线电压的恒定，同时平衡机侧输入系统的有功功率；风场内网PCC点电压和电流幅值也可得到较好的约束，且风场内网的频率基本保持恒定；DRU-HVDC在海上风场故障期间直流电流断流，直流电压出现小幅暂态波动。

图 14 故障F₁工况下风电机组的故障穿越仿真结果

Figure 14. The LVRT simulation results of WTs under the F₁ fault

下载: 全尺寸图片幻灯片

4.6 岸上电网三相短路故障穿越验证

对于岸上电网三相短路故障F₂，故障切除时间0.625 s，风电机组额定风速下的故障穿越仿真结果如图 15所示。其中故障穿越期间，尽管HVDC未使用高压直流卸荷，海上风场仍可通过机组输出电压限幅和DRU的单相导通特性，降低乃至终止DRU-HVDC的功率传输；期间机组输出的三相电压很好的约束在了1.1 pu以内，且由于机组直流卸荷作用，机组输出电流幅值下降且均为无功电流，风场频率故障穿越期间基本不受影响；DRU-HVDC电压约束在1.25 pu以内。

图 15 故障F₂工况下风电机组故障穿越仿真结果

Figure 15. The LVRT simulation results of WTs under the F₂ fault

下载: 全尺寸图片幻灯片

5. 系统交互稳定性探讨

为进一步说明本文所提集群构网控制策略应用于海上风电经DRU-HVDC送出系统的可行性。本节从海上风电场变流器间、海上风电场与DRU间的交互稳定性角度出发，分析了海上风电场不同工况下的系统交互稳定性情况，分析过程如下。

5.1 系统交互稳定性分析方法

基于换流器装备小信号阻抗的系统稳定性分析方法^[32-33]，本节重点介绍海上风电变流器集群控制策略下换流器的阻抗建模以及系统的交互稳定性分析方法。

为便于海上风电经DRU-HVDC送出系统的小扰动稳定性分析，本节在图 8仿真系统的基础上对DRU-HVDC的HVDC系统和岸上MMC换流站进一步做出简化，如图 16所示，系统参数如附表A1—A3所示。

图 16 海上风电经DRU-HVDC并网等值系统

Figure 16. Equivalent system of DRU-HVDC integrated OWF

下载: 全尺寸图片幻灯片

DRU的dq阻抗建模方法已在文献[34]中进行了详细的说明，本文不再赘述。施加本文所提海上风电变流器集群控制策略的海上风电机组dq阻抗建模于附录B中给出。进一步地，给出dq阻抗与正/负序阻抗之间的转化关系如下：

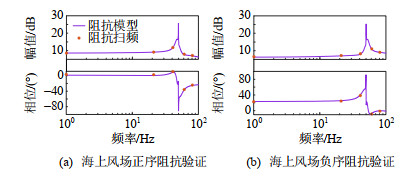
$\left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{Z_\text{pp}}}&{{Z_\text{pn}}} \\ {{Z_\text{np}}}&{{Z_\text{nn}}} \end{array}} \right] = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 1&\text{j} \\ 1&{ - \text{j}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{Z_{dd}}}&{{Z_{dq}}} \\ {{Z_{qd}}}&{{Z_{qq}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&1 \\ { - \text{j}}&\text{j} \end{array}} \right] \hfill \\ {Z_\text{p}} = {Z_\text{pp}} - \frac{{{Z_\text{pn}}{Z_\text{np}}}}{{{Z_\text{nn}}}} \hfill \\ {Z_\text{n}} = {Z_\text{nn}} - \frac{{{Z_\text{pn}}{Z_\text{np}}}}{{{Z_\text{pp}}}} \hfill \\ \end{array} \right.$

(24)

式中：Z_pp—Z_nn为序阻抗矩阵的元素；Z_dd—Z_qq为dq阻抗矩阵的元素；Z_p为正序阻抗；Z_n为负序阻抗；j为复数。PCC点左侧(海上风场)和右侧(DRU换流站)的正负序阻抗模型验证如图 17、18所示，验证了所建小信号阻抗模型的准确性。

图 17 海上风场部分小信号阻抗模型验证

Figure 17. The verification of small-signal impedance model for OWF part

下载: 全尺寸图片幻灯片

图 18 DRU换流站部分小信号阻抗模型验证

Figure 18. The verification of small-signal impedance model for DRU converter station part

下载: 全尺寸图片幻灯片

在系统稳定性分析方法方面，由于风电机组采用构网型控制，同时该研究场景中DRU也对海上风场的电压幅值具有钳位作用，故采用Z + Z系统的稳定判据^[35-36]，对互联系统的稳定性进行分析，系统的稳定性可以通过各节点左右两侧系统的阻抗和轨迹顺时针包围(0, 0)的圈数是否为0判断，故系统谐振点判据也可写作：

$\left\{ \begin{array}{l} \text{Im} [{Z_1}({\omega _\text{res}}) + {Z_2}({\omega _\text{res}})] = 0 \hfill \\ \text{Re} [{Z_1}({\omega _\text{res}}) + {Z_2}({\omega _\text{res}})] < 0 \hfill \\ \frac{{{\text{d}}\;\text{Im} [{Z_1}(\omega ) + {Z_2}(\omega )]}}{{{\text{d}}\omega }}{|_{\omega = {\omega _\text{res}}}} > 0 \hfill \\ \end{array} \right.$

(25)

式中：Im[]表示取表达式虚部；Re[]表示取表达式实部。若上述表达式成立，则可判断ω = ω_res为系统谐振点。

以下基于所建风电机组和DRU装备小信号阻抗模型，以及Z + Z型系统稳定性分析方法对系统的交互稳定性分析如下给出。

5.2 风电场负荷率变化对系统交互稳定性的影响

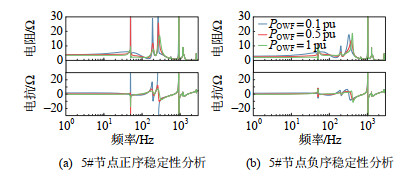
本节主要分析海上风场负荷率变化对海上风电系统交互稳定性的影响。以1#节点的阻抗和代表海上风电场部变换器间交互稳定性；以5#节点(PCC)的阻抗和代表海上风电场与DRU间的交互稳定性。在海上风场中各聚合机组负荷率一致的条件下，给出海上风场负荷率为0.1、0.5、1 pu条件下，海上风场交互稳定性的对比结果，如图 19、20所示。由图可知，海上风场负荷率从轻载到满载下，1#、5#节点的阻抗和实部在宽频内均大于0，系统稳定性良好。说明了在海上风电场负荷率变化条件下，所提机组的集群构网控制策略均可以保证海上风电场系统的交互稳定性。同时，风场负荷率变化对机组间交互稳定性影响更明显，尤其是对100~ 200 Hz间的谐振点，风场负载率越低，该谐振点处的阻抗和越小。

图 19 海上风场负荷率变化对海上风场与DRU之间交互稳定性的影响

Figure 19. The impact of load rate variation for OWFs on the interactive stability between OWF and DRU

下载: 全尺寸图片幻灯片

图 20 海上风电场负荷率变化对海上风电场内部机组间交互稳定性的影响

Figure 20. The influence of load rate change for OWFs on the interactive stability among WTs

下载: 全尺寸图片幻灯片

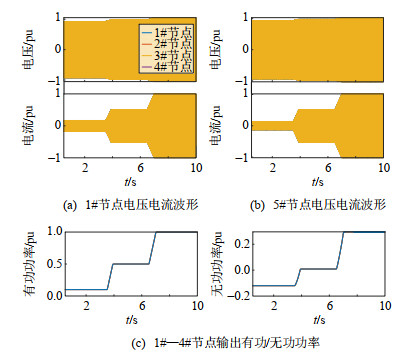
本案例条件下，海上风电场仿真结果如图 21所示。

图 21 海上风电场负荷率变化的系统仿真结果

Figure 21. System simulation results under load rate variation of OWFs

下载: 全尺寸图片幻灯片

海上风场的负荷率初始为0.1 pu，3.5 s变换为0.5 pu，6.5 s变换为1 pu，且4台聚合机组的负荷率同时变化。仿真结果说明了在海上风场负荷率变化的条件下，机组集群构网控制策略可保证海上风场的稳定运行，验证了图 19和20的理论分析结果的正确性。

5.3 风电场出力差异对系统交互稳定性的影响

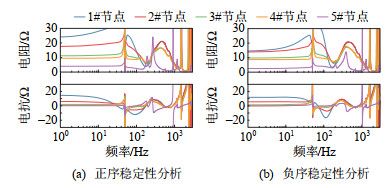
本节主要分析海上风电场出力差异对海上风电系统交互稳定性的影响。机组工作点的差异更有利于验证所提机组集群构网控制策略在机组间交互稳定性方面的影响。仿真系统中，聚合机组出力的设置如：1#机组出力设置为0 pu，2#机组出力设置为1/3 pu，3#机组出力设置为2/3 pu，4#机组出力设置为1 pu。1#—5#节点的稳定性分析结果如图 22所示。由图可知，在机组之间出力不一致的条件下，海上风场经DRU-HVDC送出系统中的全部节点阻抗和实部均大于0，故机组间的交互不会引起系统的失稳。验证了所提机组集群构网控制策略在机组间交互方面的稳定性。此外，机组出力越小，节点的稳定性越差，例如，在100~200 Hz内阻抗和虚部为0的谐振点处，1#—4#节点的阻抗和实部依次升高，同时1#—4#机组的输出功率也依次升高。与海上风场负荷率变化对海上风场系统稳定性的影响结论一致。

图 22 风电机组出力差异对海上风电场交互稳定性影响

Figure 22. The affect of different load conditions of WTs on the interactive stability of DRU-HVDC integrated OWFs

下载: 全尺寸图片幻灯片

本案例条件下，海上风电场的仿真结果如图 23所示。1#-4#聚合机组的负荷率均初始为0.1 pu，3.5 s 1#-4#聚合机组的负荷率分别变化为0、1/3、2/3和1 pu。仿真结果说明了风电机组出力差异条件下，机组集群构网控制策略可保证海上风场的稳定运行，验证了图 22的理论分析结果的正确性。

图 23 风电机组出力差异下的系统仿真结果

Figure 23. System simulation results under different load conditions of WTs

下载: 全尺寸图片幻灯片

6. 结论

本文针对构网型风电场经DRU-HVDC送出系统，完善了机组构网控制率、控制参数的设计原则及机组间的同步机理，提出了一种不影响机组载荷的机组网侧变流器集群构网控制策略，并通过仿真验证了其黑启动、稳态和故障穿越的有效性。结论如下：

1）DRU直流侧联结电压源时，其交流端口具有定电压幅值特性，并且在系统拓扑固定情况下，其功率因数与直/交流侧等值电源输入条件成单值映射，因此可采用U/PF节点对DRU的基频功率特性进行刻画，并使用BP-神经网络进行精确建模；

2）为保证风电机组的MPPT运行，海上风电汇集网应具备有功平衡节点性质，在DRU的U/PF节点特性作用下，此时系统的交流电压幅值和无功负荷由风电有功功率决定，系统的频率及无功平衡需要由风电机组来维持，故风电机组应具备ω-Q下垂控制率，并设置较大的正下垂系数以确保系统频率稳定和机组间的同步。

3）本文所提风电机组网侧变流器集群构网控制策略不影响机组载荷，可保证系统存在稳定的频率-无功平衡点与机组间的自同步，可实现海上风场的黑启动、正常运行条件下的稳定运行，稳定穿越海上及岸上交流系统的三相短路故障。

附录A. 仿真系统参数

A1 聚合机组参数

A1. Parameters of aggregated WTs

编号	参数	数值
WT₁和WT₂	额定功率/MW	440
	直流母线电压/kV	1.12
	直流母线/mF	2 200
	卸荷电阻/mΩ	1.6
	储能容量/MW	13.2
	网侧滤波电感/μH	0.465
	网侧滤波电容/mF	163.4
	箱变容量/MVA	492
	箱变变比/(kV/kV)	0.69/66
	箱变漏抗/pu	0.08
	控制延时/μs	150
WT₃和WT₄	额定容量/MW	560
	直流母线电压/kV	1.12
	直流母线/mF	2 800
	卸荷电阻/mΩ	1.3
	储能容量/MW	16.8
	网侧滤波电感/nH	365.71
	网侧滤波电容/F	0.208
	箱变容量/MVA	644
	箱变变比/(kV/kV)	0.69/66
	箱变漏抗/pu	0.08
	控制延时/μs	150

下载: 导出CSV

| 显示表格

A2 海上交流系统参数

A2. Parameters of offshore AC system

编号	参数	数值
电缆1和电缆2	聚合电阻R_c1、R_c2/mΩ	94.3
	聚合电感L_c1、L_c2/μH	408.09
	聚合电容C_c1、C_c2/μF	9.384
电缆3和电缆4	聚合电阻R_c3、R_c4/mΩ	52.98
	聚合电感L_c3、L_c4/mH	0.34
	聚合电容C_c3、C_c4/μF	15.02
整流变T₂	变比/(kV/kV)	66/400
	容量/MVA	1 120
	漏抗/pu	0.16
直流滤波器	L_dc/H	0.075
直流海缆参数	聚合电阻R_c5/Ω	2.5
	聚合电感L_c5/H	0.02
	聚合电容C_c5/μF	13

下载: 导出CSV

| 显示表格

A3 双调谐滤波器参数

A3. Parameters of double tuning filters

参数	数值	参数	数值
C₁₁/μF	70.604	C₂₁/μF	56.892
L₁₁/μH	643.82	L₂₁/μH	606.29
C₁₂/μF	112.45	C₂₂/μF	118.8
L₁₂/μH	313.74	L₂₂/μH	237.19
R₁₁/Ω	185	R₂₁/Ω	185

下载: 导出CSV

| 显示表格

A4 岸上MMC参数

A4. Parameters of the onshore MMC

参数	数值	参数	数值
额定容量/MW	2 000	直流侧额定电压/kV	±500
桥臂子模块数	476	变压器额定容量/MVA	2 160
子模块电容容值/mF	11	变压器漏抗/pu	0.16
桥臂电感/mH	120	变压器变比/(kV/kV)	570/525

下载: 导出CSV

| 显示表格

附录B. 风电变流器集群控制策略下小信号dq阻抗建模

由于直流母线的动态解耦和网侧变换器的直流电压控制，机侧系统对网侧变流器的输出动态影响可忽略，故在网侧变换器的dq阻抗模型推导过程中，将机侧系统以功率源等效且输出功率恒定，其简化系统如图B1所示。首先建立PLL的小信号闭环传函G_PLL，其可表示为

$\Delta \theta = \frac{{{H_{{\text{PLL}}}}}}{{s + {U_{{\text{f}}d{\text{ 0}}}}{H_{{\text{PLL}}}}}}\Delta U_{{\text{f}}q}^{\text{s}} = {G_{{\text{PLL}}}}\Delta U_{{\text{f}}q}^{\text{s}} = [\begin{array}{*{20}{c}} 0&{{G_{{\text{PLL}}}}} \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right]$

(B1)

B1 风电机组简化拓扑及其控制

B1. The simplified topology and control for WTs

下载: 全尺寸图片幻灯片

式中：变量的上标“s”表示电气静止坐标系；H_PLL为锁相环的PI控制器，其他变量的含义如图B1所示。

电流环小信号传函可表示为

$\begin{array}{l} \Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{m}}d}^{\text{s}}} \\ {U_{{\text{m}}q}^{\text{s}}} \end{array}} \right] = {G_{\text{d}}}{H_{\text{c}}}\Delta \left[ {\begin{array}{*{20}{c}} {I_{{\text{fref}}d}^{\text{c}}} \\ {I_{{\text{fref}}q}^{\text{c}}} \end{array}} \right] + {G_{\text{d}}}\left[ {\begin{array}{*{20}{c}} { - {H_{\text{c}}}}&{ - {\omega _0}{L_{\text{f}}}} \\ {{\omega _0}{L_{\text{f}}}}&{ - {H_{\text{c}}}} \end{array}} \right]\Delta \left[ {\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}} \\ {I_{{\text{f}}q}^{\text{s}}} \end{array}} \right] + \hfill \\ \quad \quad {G_{\text{d}}}\Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right] - (\left[ {\begin{array}{*{20}{c}} {U_{{\text{m}}q}^{\text{s}}} \\ { - U_{{\text{m}}d}^{\text{s}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} { - {H_{\text{c}}}}&{ - {\omega _0}{L_{\text{f}}}} \\ {{\omega _0}{L_{\text{f}}}}&{ - {H_{\text{c}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {I_{{\text{f}}q}^{\text{s}}} \\ { - I_{{\text{f}}d}^{\text{s}}} \end{array}} \right] - \hfill \\ \quad \quad {G_{\text{d}}}\left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}q}^{\text{s}}} \\ { - U_{{\text{f}}d}^{\text{s}}} \end{array}} \right])[\begin{array}{*{20}{c}} 0&{{G_{{\text{PLL}}}}} \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right] \hfill \\ \end{array}$

(B2)

式中：上标“c”表示控制系统的dq旋转坐标系；H_c为电流环PI控制器传函；U_mx(x = d, q)为调制电压的dq轴分量；G_d为控制延时；I_frefx为电流环输入参考。

交流电压环小信号传函可以表示为

$\begin{array}{l} \Delta I_{{\text{fref}}d}^{\text{c}} = {H_{{\text{ac}}}}\Delta {U_{{\text{f}}d{\text{ref}}}} - [\begin{array}{*{20}{c}} {{H_{{\text{ac}}}} + s{C_{\text{f}}}}&{({\omega _0} - \omega ){C_{\text{f}}}} \end{array}] \cdot \hfill \\ \quad \quad \Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right] + [\begin{array}{*{20}{c}} 1&0 \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}} \\ {I_{{\text{f}}q}^{\text{s}}} \end{array}} \right] + (I_{{\text{wt}}q{\text{0}}}^{\text{s}} - {H_{{\text{ac}}}}U_{{\text{f}}q{\text{0}}}^{\text{s}} + \hfill \\ \quad \quad {\omega _0}CU_{{\text{f}}d{\text{0}}}^{\text{s}})[\begin{array}{*{20}{c}} 0&{{G_{{\text{PLL}}}}} \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right] \hfill \\ \end{array}$

(B3)

式中：H_ac为交流电压环PI控制器；ω为系统频率；ω₀为系统额定频率，其他变量含义与前文一致。

直流电压环的小信号传函可表示为

$\Delta {U_{{\text{f}}d{\text{ref}}}} = {H_{{\text{dc}}}}\Delta {U_{{\text{dc}}}}$

(B4)

式中H_dc为直流电压环PI控制器。

无功环的小信号传函可表示为

$\begin{array}{l} \Delta I_{{\text{fref}}q}^{\text{c}} = \frac{3}{2}{H_{\text{Q}}}[\begin{array}{*{20}{c}} {U_{{\text{f}}q{\text{0}}}^{\text{s}}}&{ - U_{{\text{f}}d{\text{0}}}^{\text{s}}} \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}} \\ {I_{{\text{f}}q}^{\text{s}}} \end{array}} \right] + \frac{3}{2}{H_{\text{Q}}} \cdot \hfill \\ \quad \quad [\begin{array}{*{20}{c}} { - I_{{\text{f}}q{\text{0}}}^{\text{s}}}&{I_{{\text{f}}d{\text{0}}}^{\text{s}}} \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right] - {H_{\text{Q}}}\Delta {Q_{{\text{ref}}}} \hfill \\ \end{array}$

(B5)

式中H_Q为无功环PI控制器。

频率-无功下垂环的小信号传函可表示为

$\Delta {Q_{{\text{ref}}}} = {K_{\mathtt{ω}{\text{Q}}}}s[\begin{array}{*{20}{c}} 0&{{G_{{\text{PLL}}}}} \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right]$

(B6)

基于机侧系统等值为恒功率源的假设，机组直交流侧间的动态关系可以表示为

$\begin{array}{l} - {U_{{\text{dc0}}}}s{C_{{\text{bus}}}}\Delta {U_{{\text{dc}}}} = \frac{3}{2}[\begin{array}{*{20}{c}} {U_{{\text{c}}d{\text{0}}}^{\text{s}}}&{U_{{\text{c}}q{\text{0}}}^{\text{s}}} \end{array}]\Delta \left[ {\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}} \\ {I_{{\text{f}}q}^{\text{s}}} \end{array}} \right] + \hfill \\ \quad \quad \frac{3}{2}[\begin{array}{*{20}{c}} {I_{{\text{f}}d{\text{0}}}^{\text{s}}}&{I_{{\text{f}}q{\text{0}}}^{\text{s}}} \end{array}](\left[ {\begin{array}{*{20}{c}} {s{L_{\text{f}}}}&{ - \omega {L_{\text{f}}}} \\ {\omega {L_{\text{f}}}}&{s{L_{\text{f}}}} \end{array}} \right]\Delta \left[ {\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}} \\ {I_{{\text{f}}q}^{\text{s}}} \end{array}} \right] + \Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{f}}d}^{\text{s}}} \\ {U_{{\text{f}}q}^{\text{s}}} \end{array}} \right]) \hfill \\ \end{array}$

(B7)

使用直接调制时，机组网侧变换器输出电压与调制电压之间的动态可以表示为

$\Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{c}}d}^{\text{s}}} \\ {U_{{\text{c}}q}^{\text{s}}} \end{array}} \right] = \frac{1}{{{U_{{\text{dc0}}}}}}\left[ {\begin{array}{*{20}{c}} {U_{{\text{m}}d{\text{0}}}^{\text{s}}} \\ {U_{{\text{m}}q{\text{0}}}^{\text{s}}} \end{array}} \right]\Delta {U_{{\text{dc}}}} + \Delta \left[ {\begin{array}{*{20}{c}} {U_{{\text{m}}d}^{\text{s}}} \\ {U_{{\text{m}}q}^{\text{s}}} \end{array}} \right]$

(B8)

式中U_cx(x = d, q)为变换器输出电压的dq轴分量，其他变量含义与前文一致。

联立式(B1)—(B8)，风电机组的小信号dq轴阻抗可以表示为

$\left\{ \begin{array}{l} \Delta\left[\begin{array}{c} U_{\mathrm{f} d}^{\mathrm{s}} \\ U_{\mathrm{f} q}^{\mathrm{s}} \end{array}\right]=-\frac{\boldsymbol{G}_{\mathrm{cI}}-\boldsymbol{G}_{\mathrm{Z}}+\boldsymbol{G}_{d \mathrm{I}}+\boldsymbol{G}_{q \mathrm{I}}+\boldsymbol{G}_{\mathrm{mI}}}{I-\boldsymbol{G}_{\mathrm{d}}-\boldsymbol{G}_{\mathrm{cPLLU}}-\boldsymbol{G}_{\mathrm{mU}}-\boldsymbol{G}_{d \mathrm{U}}-\boldsymbol{G}_{q \mathrm{U}}} \Delta\left[\begin{array}{c} I_{\mathrm{f} d}^{\mathrm{s}} \\ I_{\mathrm{f} q}^{\mathrm{s}} \end{array}\right] \\ \boldsymbol{G}_{\mathrm{d}}=\mathrm{e}^{-s T_{\mathrm{d}}} \boldsymbol{I} \\ \begin{array}{l} \boldsymbol{G}_{\mathrm{cI}}=\boldsymbol{G}_{\mathrm{d}}\left[\begin{array}{cc} -H_{\mathrm{c}} & -\omega_0 L_{\mathrm{f}} \\ \omega_0 L_{\mathrm{f}} & -H_{\mathrm{c}} \end{array}\right] \\ \boldsymbol{G}_{\mathrm{Z}}=\left[\begin{array}{cc} s L_{\mathrm{f}} & -\omega_0 L_{\mathrm{f}} \\ \omega_0 L_{\mathrm{f}} & s L_{\mathrm{f}} \end{array}\right] \end{array} \\ {\boldsymbol{G}_{d\text{I}}} = {\boldsymbol{G}_\text{d}}{\boldsymbol{H}_\text{c}}\left[ {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right]\langle \frac{{ - 1.5{H_\text{dc}}{H_\text{ac}}}}{{sC{U_\text{dc}}}}([\begin{array}{*{20}{c}} {U_{{\text{m}}d{\text{ 0}}}^{\text{s}}}&{U_{{\text{m}}q{\text{ 0}}}^{\text{s}}} \end{array}] + \hfill \\ \quad \quad\;\;\; [\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}}&{I_{{\text{f}}q}^{\text{s}}} \end{array}]{\boldsymbol{G}_\text{Z}}) + [\begin{array}{*{20}{c}} 1&0 \end{array}]\rangle \hfill \\ {\boldsymbol{G}_{q\text{I}}} = {\boldsymbol{G}_\text{d}}{\boldsymbol{H}_\text{c}}\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right]1.5{H_\text{Q}}[\begin{array}{*{20}{c}} {U_{{\text{f}}q{\text{0}}}^{\text{s}}}&{ - U_{{\text{f}}d{\text{0}}}^{\text{s}}} \end{array}] \hfill \\ {\boldsymbol{G}_\text{mI}} = \frac{{ - 1.5}}{{s{C_\text{bus}}U_\text{dc0}^2}}\left[ {\begin{array}{*{20}{c}} {U_{{\text{m}}d{\text{ 0}}}^{\text{s}}} \\ {U_{{\text{m}}q{\text{ 0}}}^{\text{s}}} \end{array}} \right]([\begin{array}{*{20}{c}} {U_{{\text{m}}d{\text{ 0}}}^{\text{s}}}&{U_{{\text{m}}q{\text{ 0}}}^{\text{s}}} \end{array}] + [\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}}&{I_{{\text{f}}q}^{\text{s}}} \end{array}]{\boldsymbol{G}_\text{Z}}) \hfill \\ {\boldsymbol{G}_\text{cPLLU}} = - ([\begin{array}{*{20}{c}} {U_{{\text{m}}d{\text{ 0}}}^{\text{s}}}&{U_{{\text{m}}q{\text{ 0}}}^{\text{s}}} \end{array}] - {\boldsymbol{G}_\text{cI}}[\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}}&{I_{{\text{f}}q}^{\text{s}}} \end{array}] - \hfill \\ \quad \quad\;\; {\boldsymbol{G}_\text{d}}[\begin{array}{*{20}{c}} {U_{{\text{f}}q{\text{0}}}^{\text{s}}}&{ - U_{{\text{f}}d{\text{ 0}}}^{\text{s}}} \end{array}])[\begin{array}{*{20}{c}} 0&{{G_\text{PLL}}} \end{array}] \hfill \\ {\boldsymbol{G}_\text{mU}} = \frac{{ - 1.5}}{{s{C_\text{bus}}U_\text{dc0}^2}}\left[ {\begin{array}{*{20}{c}} {U_{{\text{m}}d{\text{ 0}}}^{\text{s}}} \\ {U_{{\text{m}}q{\text{ 0}}}^{\text{s}}} \end{array}} \right][\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}}&{I_{{\text{f}}q}^{\text{s}}} \end{array}] \hfill \\ {\boldsymbol{G}_{d\text{U}}} = {\boldsymbol{G}_\text{d}}{\boldsymbol{H}_\text{c}}\left[ {\begin{array}{*{20}{c}} { - 1} \\ 0 \end{array}} \right][{\left[ {\begin{array}{*{20}{c}} {{H_{{\text{ac}}}} + s{C_{\text{f}}}} \\ {({H_{{\text{ac}}}}U_{{\text{f}}q{\text{0}}}^{\text{s}} - {\omega _0}{C_{\text{f}}}U_{{\text{f}}d{\text{0}}}^{\text{s}} - I_{{\text{wt}}q{\text{0}}}^{\text{s}}){G_{{\text{PLL}}}}} \end{array}} \right]^{\text{T}}} + \hfill \\ \quad \quad\;\; \frac{{1.5{H_{{\text{dc}}}}{H_{{\text{ac}}}}}}{{sC{U_{{\text{dc}}}}}}[\begin{array}{*{20}{c}} {I_{{\text{f}}d}^{\text{s}}}&{I_{{\text{f}}q}^{\text{s}}} \end{array}]] \hfill \\ {\boldsymbol{G}_{q\text{U}}} = {\boldsymbol{G}_\text{d}}{\boldsymbol{H}_\text{c}}\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right](1.5{H_\text{Q}}[\begin{array}{*{20}{c}} { - I_{{\text{f}}d}^{\text{s}}}&{I_{{\text{f}}q}^{\text{s}}} \end{array}] - {H_{\text{Q}}}{K_{{\text{f}}q}}s[\begin{array}{*{20}{c}} 0&{{G_{{\text{PLL}}}}} \end{array}]) \hfill \\ \end{array} \right.$

(B9)

图 1 海上风电场经DRU-HVDC送出并网系统

Figure 1. The DRU-HVDC integrated OWFs

下载: 全尺寸图片幻灯片

图 2 海上风电场汇集网等值系统

Figure 2. The equivalent system of offshore ac grid

下载: 全尺寸图片幻灯片

图 3 系统的电压/频率平衡点构建机理

Figure 3. The principle for constructing the system voltage/frequency equilibrium point

下载: 全尺寸图片幻灯片

图 4 一种基于PLL与ω-Q下垂同步的机组集群构网控制

Figure 4. The PLL and ω-Q droop-synchronized group GFM control of WTs

下载: 全尺寸图片幻灯片

图 5 风电场单机聚合经DRU-HVDC送出系统

Figure 5. DRU-HVDC integrated single-wind turbine aggregated OWF system

下载: 全尺寸图片幻灯片

图 6 风电场多机聚合经DRU-HVDC送出并网系统

Figure 6. DRU-HVDC integrated multi-wind turbine aggregated OWF system

下载: 全尺寸图片幻灯片

图 7 风电机组间的同步过程

Figure 7. The synchronization process among WTGs

下载: 全尺寸图片幻灯片

图 8 海上风电场经DRU-HVDC送出并网仿真系统

Figure 8. The simulation system of DRU-HVDC integrated OWF

下载: 全尺寸图片幻灯片

图 9 海上风电场经12脉DRU-HVDC送出简化系统

Figure 9. The simplified system of 12-pulse DRU-HVDC integrated OWF

下载: 全尺寸图片幻灯片

图 10 BP-神经网络的优化及准确性验证

Figure 10. The optimization and accuracy verification of BP-neural network model

下载: 全尺寸图片幻灯片

图 11 BP-神经网络模型的泛化能力验证

Figure 11. The validation of the generalization capability of BP-neural network model

下载: 全尺寸图片幻灯片

图 12 DRU输入有功/无功功率分析仿真验证

Figure 12. The simulation verification for the input active and reactive power analysis of the DRU

下载: 全尺寸图片幻灯片

图 13 海上风场经DRU-HVDC送出系统黑启动至额定运行仿真结果

Figure 13. The simulation results of DRU-HVDC integrated OWF from black start to rated operation condition

下载: 全尺寸图片幻灯片

图 14 故障F₁工况下风电机组的故障穿越仿真结果

Figure 14. The LVRT simulation results of WTs under the F₁ fault

下载: 全尺寸图片幻灯片

图 15 故障F₂工况下风电机组故障穿越仿真结果

Figure 15. The LVRT simulation results of WTs under the F₂ fault

下载: 全尺寸图片幻灯片

图 16 海上风电经DRU-HVDC并网等值系统

Figure 16. Equivalent system of DRU-HVDC integrated OWF

下载: 全尺寸图片幻灯片

图 17 海上风场部分小信号阻抗模型验证

Figure 17. The verification of small-signal impedance model for OWF part

下载: 全尺寸图片幻灯片

图 18 DRU换流站部分小信号阻抗模型验证

Figure 18. The verification of small-signal impedance model for DRU converter station part

下载: 全尺寸图片幻灯片

图 19 海上风场负荷率变化对海上风场与DRU之间交互稳定性的影响

Figure 19. The impact of load rate variation for OWFs on the interactive stability between OWF and DRU

下载: 全尺寸图片幻灯片

图 20 海上风电场负荷率变化对海上风电场内部机组间交互稳定性的影响

Figure 20. The influence of load rate change for OWFs on the interactive stability among WTs

下载: 全尺寸图片幻灯片

图 21 海上风电场负荷率变化的系统仿真结果

Figure 21. System simulation results under load rate variation of OWFs

下载: 全尺寸图片幻灯片

图 22 风电机组出力差异对海上风电场交互稳定性影响

Figure 22. The affect of different load conditions of WTs on the interactive stability of DRU-HVDC integrated OWFs

下载: 全尺寸图片幻灯片

图 23 风电机组出力差异下的系统仿真结果

Figure 23. System simulation results under different load conditions of WTs

下载: 全尺寸图片幻灯片

B1 风电机组简化拓扑及其控制

B1. The simplified topology and control for WTs

下载: 全尺寸图片幻灯片

A1 聚合机组参数

A1 Parameters of aggregated WTs

编号	参数	数值
WT₁和WT₂	额定功率/MW	440
	直流母线电压/kV	1.12
	直流母线/mF	2 200
	卸荷电阻/mΩ	1.6
	储能容量/MW	13.2
	网侧滤波电感/μH	0.465
	网侧滤波电容/mF	163.4
	箱变容量/MVA	492
	箱变变比/(kV/kV)	0.69/66
	箱变漏抗/pu	0.08
	控制延时/μs	150
WT₃和WT₄	额定容量/MW	560
	直流母线电压/kV	1.12
	直流母线/mF	2 800
	卸荷电阻/mΩ	1.3
	储能容量/MW	16.8
	网侧滤波电感/nH	365.71
	网侧滤波电容/F	0.208
	箱变容量/MVA	644
	箱变变比/(kV/kV)	0.69/66
	箱变漏抗/pu	0.08
	控制延时/μs	150

下载: 导出CSV

A2 海上交流系统参数

A2 Parameters of offshore AC system

编号	参数	数值
电缆1和电缆2	聚合电阻R_c1、R_c2/mΩ	94.3
	聚合电感L_c1、L_c2/μH	408.09
	聚合电容C_c1、C_c2/μF	9.384
电缆3和电缆4	聚合电阻R_c3、R_c4/mΩ	52.98
	聚合电感L_c3、L_c4/mH	0.34
	聚合电容C_c3、C_c4/μF	15.02
整流变T₂	变比/(kV/kV)	66/400
	容量/MVA	1 120
	漏抗/pu	0.16
直流滤波器	L_dc/H	0.075
直流海缆参数	聚合电阻R_c5/Ω	2.5
	聚合电感L_c5/H	0.02
	聚合电容C_c5/μF	13

下载: 导出CSV

A3 双调谐滤波器参数

A3 Parameters of double tuning filters

参数	数值	参数	数值
C₁₁/μF	70.604	C₂₁/μF	56.892
L₁₁/μH	643.82	L₂₁/μH	606.29
C₁₂/μF	112.45	C₂₂/μF	118.8
L₁₂/μH	313.74	L₂₂/μH	237.19
R₁₁/Ω	185	R₂₁/Ω	185

下载: 导出CSV

A4 岸上MMC参数

A4 Parameters of the onshore MMC

参数	数值	参数	数值
额定容量/MW	2 000	直流侧额定电压/kV	±500
桥臂子模块数	476	变压器额定容量/MVA	2 160
子模块电容容值/mF	11	变压器漏抗/pu	0.16
桥臂电感/mH	120	变压器变比/(kV/kV)	570/525

下载: 导出CSV

参考文献(36)

[1]	金砚秋, 张哲任, 吴宏远, 等. 基于构网型风电机组和二极管整流单元的海上风电场黑启动策略[J]. 高电压技术, 2023, 49(9): 3730-3740. JIN Yanqiu, ZHANG Zheren, WU Hongyuan, et al. Black start strategy of offshore wind farm based on grid-forming wind turbines and diode rectifier unit[J]. High Voltage Engineering, 2023, 49(9): 3730-3740(in Chinese).
[2]	金国彬, 杨明城, 李国庆, 等. 考虑小干扰稳定的海上风电经不控整流直流送出系统控制器参数优化设计[J]. 电力系统保护与控制, 2022, 50(21): 65-74. JIN Guobin, YANG Mingcheng, LI Guoqing, et al. Optimization design of controller parameters for an offshore wind power DC output system by diode rectifier considering small signal stability[J]. Power System Protection and Control, 2022, 50(21): 65-74(in Chinese).
[3]	方梓熙, 蔡旭, 史先强, 等. 混合型海上风电直流换流器的拓扑优化与控制[J]. 中国电机工程学报, 2021, 41(24): 8546-8559. DOI: 10.13334/j.0258-8013.pcsee.201927 FANG Zixi, CAI Xu, SHI Xianqiang, et al. Topology optimization and control of the hybrid DC converter for offshore wind farms[J]. Proceedings of the CSEE, 2021, 41(24): 8546-8559(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.201927
[4]	秦世耀, 齐琛, 李少林, 等. 电压源型构网风电机组研究现状及展望[J]. 中国电机工程学报, 2023, 43(4): 1314-1333. DOI: 10.13334/j.0258-8013.pcsee.222095 QIN Shiyao, QI Chen, LI Shaolin, et al. Review of the voltage-source grid forming wind turbine[J]. Proceedings of the CSEE, 2023, 43(4): 1314-1333(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.222095
[5]	XIAO Huangqing, HUANG Xiaowei, HUANG Ying, et al. Self-synchronizing control and frequency response of offshore wind farms connected to diode rectifier based HVDC system[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1681-1692. DOI: 10.1109/TSTE.2022.3170717
[6]	TANG Yingjie, ZHANG Zheren, XU Zheng. DRU based low frequency AC transmission scheme for offshore wind farm integration[J]. IEEE Transactions on Sustainable Energy, 2021, 12(3): 1512-1524. DOI: 10.1109/TSTE.2021.3053051
[7]	YU Lujie, LI Rui, XU Lie, et al. Distributed PLL-based control of offshore wind turbines connected with diode-rectifier-based HVDC systems[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1328-1336. DOI: 10.1109/TPWRD.2017.2772342
[8]	CARDIEL-ÁLVAREZ M Á, ARNALTES S, RODRIGUEZ-AMENEDO J L, et al. Decentralized control of offshore wind farms connected to diode-based HVdc links[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1233-1241. DOI: 10.1109/TEC.2018.2804662
[9]	PRIGNITZ C, ECKEL H G, ACHENBACH S, et al. FixReF: a control strategy for offshore wind farms with different wind turbine types and diode rectifier HVDC transmission[C]//Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems. Vancouver, BC, Canada: IEEE, 2016: 1-7.
[10]	PRIGNITZ C, ECKEL H G, KNAAK H J. Voltage and current behavior in a FixReF controlled offshore wind farm using a HVDC transmission system based on uncontrolled diode rectifier units[C]//Proceedings of the 2016 18th European Conference on Power Electronics and Applications. Karlsruhe, Germany: IEEE, 2016: 1-6.
[11]	BLASCO-GIMENEZ R, AÑÓ-VILLALBA S, RODRÍGUEZ-D'DERLÉE J, et al. Distributed Voltage and frequency control of offshore wind farms connected with a diode-based HVDC link[J]. IEEE Transactions on Power Electronics, 2010, 25(12): 3095-3105. DOI: 10.1109/TPEL.2010.2086491
[12]	BIDADFAR A, SABORÍO-ROMANO O, CUTULULIS N A, et al. Control of offshore wind turbines connected to diode-rectifier-based HVdc systems[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 514-523. DOI: 10.1109/TSTE.2020.3008606
[13]	YU Lujie, MIAO Shuohui, ZHU Shuohui, et al. Self-synchronization control of offshore wind turbines connected with DRU-HVDC[J]. CSEE Journal of Power and Energy Systems, doi: 10.17775/CSEEJPES.2022.03690.
[14]	ZHANG Zheren, JIN Yanqiu, XU Zheng. Grid-forming control of wind turbines for diode rectifier unit based offshore wind farm integration[J]. IEEE Transactions on Power Delivery, 2023, 38(2): 1341-1352. DOI: 10.1109/TPWRD.2022.3213665
[15]	肖晃庆, 黄小威, 李岩, 等. 适用于二极管不控整流送出的海上风电机组无功功率同步控制策略[J]. 高电压技术, 2022, 48(10): 3820-3828. XIAO Huangqing, HUANG Xiaowei, LI Yan, et al. Reactive power-synchronization control for offshore wind turbines connected to diode rectifier[J]. High Voltage Engineering, 2022, 48(10): 3820-3828(in Chinese).
[16]	俞露杰, 付子玉, 朱介北, 等. 远海风电DRU-HVDC送出系统构网控制与启动方法综述[J]. 电力系统自动化, 2023, 47(24): 63-79. YU Lujie, FU Ziyu, ZHU Jiebei, et al. Review on grid-forming control and start-up method of diode-rectifier-unit based HVDC transmission system for remote offshore wind farm[J]. Automation of Electric Power Systems, 2023, 47(24): 63-79(in Chinese).
[17]	HERRERA D, TRICARICO T, OLIVEIRA D, et al. Advanced local grid control system for offshore wind turbines with the diode-based rectifier HVDC link implemented in a true scalable test bench[J]. Energies, 2022, 15(16): 5826. DOI: 10.3390/en15165826
[18]	YU Lujie, LI Rui, XU Lie, et al. Analysis and control of offshore wind farms connected with diode rectifier-based HVDC system[J]. IEEE Transactions on Power Delivery, 2020, 35(4): 2049-2059. DOI: 10.1109/TPWRD.2019.2960405
[19]	张哲任, 金砚秋, 徐政. 两种基于构网型风机和二极管整流单元的海上风电送出方案[J]. 高电压技术, 2022, 48(6): 2098-2107. ZHANG Zheren, JIN Yanqiu, XU Zheng. Two offshore wind farm integration schemes based on grid forming wind turbines and diode rectifier unit[J]. High Voltage Engineering, 2022, 48(6): 2098-2107(in Chinese).
[20]	YU Haotian, LIU Li, YANG Renxin, et al. Stability analysis and parameter optimization for DRU connected grid-forming offshore wind turbines[C]//Proceedings of the 2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems. Shanghai, China: IEEE, 2023: 261-268.
[21]	饶仪明, 吕敬, 王众, 等. 基于数据-模型融合驱动的新能源场站宽频阻抗在线辨识及稳定性评估[J]. 中国电机工程学报, 2024, 44(7): 2670-2684. DOI: 10.13334/j.0258-8013.pcsee.222536 RAO Yiming, LYU Jing, WANG Zhong, et al. Wideband impedance online identification and stability assessment of renewable power plants based on physics-informed data-driven method[J]. Proceedings of the CSEE, 2024, 44(7): 2670-2684(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.222536
[22]	王景芳, 赵晨, 姚绪梁, 等. 一种基于改进双二极管脉波倍增电路的串联型24脉波整流器[J]. 中国电机工程学报, 2024, 44(12): 4878-4891. DOI: 10.13334/j.0258-8013.pcsee.223382 WANG Jingfang, ZHAO Chen, YAO Xuliang, et al. A series-connected 24-pulse rectifier based on improved dual-diode pulse-doubling circuit[J]. Proceedings of the CSEE, 2024, 44(12): 4878-4891(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.223382
[23]	CHEN Lin, XIE Yunxiang. Analysis of three-phase bridge rectifier with constant voltage loads[C]//Proceedings of 2010 International Conference on Electrical and Control Engineering. Wuhan, China: IEEE, 2010: 3347-3350.
[24]	王德胜, 颜湘武, 贾焦心, 等. 永磁直驱风机基于虚拟同步技术的高、低电压连续故障穿越策略[J]. 中国电机工程学报, 2022, 42(6): 2164-2174. DOI: 10.13334/j.0258-8013.pcsee.212214 WANG Desheng, YAN Xiangwu, JIA Jiaoxin, et al. High/low voltage continuous fault ride through strategy of PMSGs based on virtual synchronization technology[J]. Proceedings of the CSEE, 2022, 42(6): 2164-2174(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.212214
[25]	MOLINA-GORDILLO S, SANTO-CHILUISA M, LLANOS-PROAÑO J, et al. Comparison of DC-Link voltage control architectures on grid-side and machine-side for permanent magnet synchronous generator connected to the grid[C]//Proceedings of the 2022 IEEE Sixth Ecuador Technical Chapters Meeting. Quito, Ecuador: IEEE, 2022: 1-7.
[26]	饶仪明, 吕敬, 戴金水, 等. 不同控制策略下直驱风电机组的机网耦合特性及稳定性分析[J]. 电力系统自动化, 2024, 48(4): 150-159. RAO Yiming, LYU Jing, DAI Jinshui, et al. Analysis of generator-grid coupling characteristics and stability for direct-drive wind turbines with different control strategies [J]. Automation of Electric Power Systems, 2024, 48(4): 150-159(in Chinese).
[27]	中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 15945—2008电能质量电力系统频率偏差[S]. 北京: 中国标准出版社, 2008. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration. GB/T 15945—2008 Power quality: Frequency deviation for power system[S]. Beijing: Standards Press of China, 2008(in Chinese).
[28]	QIN Yao, WANG Xiaohe, WANG Han, et al. Effect of submarine cable capacitance on dynamic aggregation modeling of SCIG-based wind farm[C]//Proceedings of the 2020 4th International Conference on HVDC. Xi'an, China: IEEE, 2020: 651-656.
[29]	SHAO Haoshu, YAN Heming, CAI Xu, et al. Aggregation modeling algorithm of PMSM wind farm considering submarine cable power loss[C]//Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition-Asia. Singapore: IEEE, 2021: 1169-1174.
[30]	MARTÍNEZ-TURÉGANO J, AÑÓ-VILLALBA S, CHAQUES-HERRAIZ G, et al. Model aggregation of large wind farms for dynamic studies[C]//Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society. Beijing, China: IEEE, 2017: 316-321.
[31]	MARTÍNEZ-TURÉGANO J, AÑÓ-VILLALBA S, BERNAL-PEREZ S, et al. Aggregation of type-4 large wind farms based on admittance model order reduction [J]. Energies, 2019, 12(9): 1730.
[32]	宗皓翔, 张琛, 蔡旭. 电力电子主导的交直流混联电网振荡分析与评估[J]. 中国电机工程学报, 2023, 43(10): 3844-3855. DOI: 10.13334/j.0258-8013.pcsee.212596 ZONG Haoxiang, ZHANG Chen, CAI Xu. Oscillation analysis and evaluation of the power electronics-dominated hybrid AC/DC grid[J]. Proceedings of the CSEE, 2023, 43(10): 3844-3855(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.212596
[33]	于浩天, 吕敬, 蔡旭, 等. 一种动态性能友好型柔性直流输电系统高频自稳控制策略[J]. 中国电机工程学报, 2023, 43(9): 3293-3307. DOI: 10.13334/j.0258-8013.pcsee.220934 YU Haotian, LYU Jing, CAI Xu, et al. A dynamic performance-friendly high-frequency self-stabilizing control method for flexible HVDC system[J]. Proceedings of the CSEE, 2023, 43(9): 3293-3307(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.220934
[34]	YU Lujie, XU Lie, ZHU Jiebei, et al. Impedance modelling and stability analysis of diode-rectifier based HVDC connected offshore wind farms[J]. IEEE Transactions on Power Delivery, 2022, 37(1): 591-602.
[35]	REN Xinfang, YU Haotian, CAI Xu, et al. A parameter design method for DRU-HVDC integrated offshore wind farm concerning system harmonic and resonance characteristics[C]//Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium. Guangzhou, China: IEEE, 2023: 1111-1116.
[36]	满九方, 谢小荣, 陈垒, 等. 柔性直流输电系统高频振荡建模分析与抑制策略综述[J]. 中国电机工程学报, 2023, 43(9): 3308-3321. DOI: 10.13334/j.0258-8013.pcsee.221064 MAN Jiufang, XIE Xiaorong, CHEN Lei, et al. Overview of modeling analysis and mitigation strategies of high-frequency resonance in mmc-hvdc systems[J]. Proceedings of the CSEE, 2023, 43(9): 3308-3321(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.221064

施引文献

资源附件(0)

图(24) / 表(4)

计量

文章访问数: 0
HTML全文浏览量: 0
PDF下载量: 0
被引次数: 0

0. 引言
1. 海上风电场经DRU-HVDC送出系统拓扑
2. 经DRU-HVDC送出的风电场运行特性分析
2.1 DRU交流端口的U/PF节点特性建模
2.2 风电场汇集网运行特性分析
2.2.1 风电场汇集网的等效负荷特性
2.2.2 风电场汇集网的电压/频率构建机理
2.2.3 风电机组控制率的设计要求
3. 一种海上风电变流器集群构网控制策略
3.1 风电机组构网控制策略设计
3.2 ω-Q下垂增益的设计原则
3.3 风电机组的构网控制同步机理
4. 仿真验证
4.1 仿真系统
4.2 DRU交流端口U/PF节点特性建模方法验证
4.3 海上风电场的功率传输特性验证
4.4 海上风电场的黑启动及稳态运行验证
4.5 海上电网三相短路故障穿越验证
4.6 岸上电网三相短路故障穿越验证
5. 系统交互稳定性探讨
5.1 系统交互稳定性分析方法
5.2 风电场负荷率变化对系统交互稳定性的影响
5.3 风电场出力差异对系统交互稳定性的影响
6. 结论
附录A. 仿真系统参数
附录B. 风电变流器集群控制策略下小信号dq阻抗建模

0. 引言
1. 海上风电场经DRU-HVDC送出系统拓扑
2. 经DRU-HVDC送出的风电场运行特性分析
2.1 DRU交流端口的U/PF节点特性建模
2.2 风电场汇集网运行特性分析
2.2.1 风电场汇集网的等效负荷特性
2.2.2 风电场汇集网的电压/频率构建机理
2.2.3 风电机组控制率的设计要求
3. 一种海上风电变流器集群构网控制策略
3.1 风电机组构网控制策略设计
3.2 ω-Q下垂增益的设计原则
3.3 风电机组的构网控制同步机理
4. 仿真验证
4.1 仿真系统
4.2 DRU交流端口U/PF节点特性建模方法验证
4.3 海上风电场的功率传输特性验证
4.4 海上风电场的黑启动及稳态运行验证
4.5 海上电网三相短路故障穿越验证
4.6 岸上电网三相短路故障穿越验证
5. 系统交互稳定性探讨
5.1 系统交互稳定性分析方法
5.2 风电场负荷率变化对系统交互稳定性的影响
5.3 风电场出力差异对系统交互稳定性的影响
6. 结论
附录A. 仿真系统参数
附录B. 风电变流器集群控制策略下小信号dq阻抗建模

参考文献(36)

施引文献

资源附件(0)

经DRU-HVDC送出的海上风电场汇集网电气调节特性分析及集群构网控制策略

通讯作者: 杨仁炘(1992)，男，博士，助理研究员，研究方向为柔性直流输电技术及可再生能源友好并网技术，frank_yang@sjtu.edu.cn

计量

出版历程

Analysis of Electrical Regulation Characteristics and Group Grid-forming Control Strategy of DRU-HVDC Integrated Offshore Wind Farm

0. 引言

1. 海上风电场经DRU-HVDC送出系统拓扑

2. 经DRU-HVDC送出的风电场运行特性分析

2.1 DRU交流端口的U/PF节点特性建模

2.2 风电场汇集网运行特性分析

2.2.1 风电场汇集网的等效负荷特性

2.2.2 风电场汇集网的电压/频率构建机理

2.2.3 风电机组控制率的设计要求

3. 一种海上风电变流器集群构网控制策略

3.1 风电机组构网控制策略设计

3.2 ω-Q下垂增益的设计原则

3.3 风电机组的构网控制同步机理

4. 仿真验证

4.1 仿真系统

4.2 DRU交流端口U/PF节点特性建模方法验证

4.3 海上风电场的功率传输特性验证

4.4 海上风电场的黑启动及稳态运行验证

4.5 海上电网三相短路故障穿越验证

4.6 岸上电网三相短路故障穿越验证

5. 系统交互稳定性探讨

5.1 系统交互稳定性分析方法

5.2 风电场负荷率变化对系统交互稳定性的影响

5.3 风电场出力差异对系统交互稳定性的影响

6. 结论

附录A. 仿真系统参数

附录B. 风电变流器集群控制策略下小信号dq阻抗建模

计量

出版历程

目录

0. 引言

1. 海上风电场经DRU-HVDC送出系统拓扑

2. 经DRU-HVDC送出的风电场运行特性分析

2.1 DRU交流端口的U/PF节点特性建模

2.2 风电场汇集网运行特性分析

2.2.1 风电场汇集网的等效负荷特性

2.2.2 风电场汇集网的电压/频率构建机理

2.2.3 风电机组控制率的设计要求

3. 一种海上风电变流器集群构网控制策略

3.1 风电机组构网控制策略设计

3.2 ω-Q下垂增益的设计原则

3.3 风电机组的构网控制同步机理

4. 仿真验证

4.1 仿真系统

4.2 DRU交流端口U/PF节点特性建模方法验证

4.3 海上风电场的功率传输特性验证

4.4 海上风电场的黑启动及稳态运行验证

4.5 海上电网三相短路故障穿越验证

4.6 岸上电网三相短路故障穿越验证

5. 系统交互稳定性探讨

5.1 系统交互稳定性分析方法

5.2 风电场负荷率变化对系统交互稳定性的影响

5.3 风电场出力差异对系统交互稳定性的影响

6. 结论

附录A. 仿真系统参数

附录B. 风电变流器集群控制策略下小信号dq阻抗建模

通讯作者:
杨仁炘(1992)，男，博士，助理研究员，研究方向为柔性直流输电技术及可再生能源友好并网技术，frank_yang@sjtu.edu.cn