500 kV耐张型悬索支撑输电体系动力整体可靠性分析

王邦杰; 王涛; 李茂华; 李正良; 吕大刚; 谭忆秋

doi:10.13334/j.0258-8013.pcsee.232388

500 kV耐张型悬索支撑输电体系动力整体可靠性分析

1.
重庆大学土木工程学院, 重庆市沙坪坝区 400045
2.
哈尔滨工业大学交通科学与工程学院, 黑龙江省哈尔滨市 150090
3.
中国电力科学研究院有限公司, 北京市西城区 100055
4.
哈尔滨工业大学土木工程学院, 黑龙江省哈尔滨市 150090

基金项目:

国家电网有限公司科技项目 5200-202156071A-0-0-00

重庆市自然科学基金项目 CSTB2024NSCQ-MSX1134

重庆市自然科学基金创新发展联合基金项目 CSTB2023NSCQ-LZX0080

详细信息

作者简介:
王邦杰(1999)，男，博士研究生，主要研究方向为输电结构风致振动和安全评估，bangjiewang@cqu.edu.cn

李茂华(1978)，女，博士，高级工程师，主要研究方向为输电线路结构设计及研究，limaohua@epri.sgcc.com.cn

通讯作者:
王涛(1993)，男，博士，主要研究方向为结构振动与安全风险评估，taowang@alu.cqu.edu.cn

中图分类号: TU351
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2023-10-30
- 发布日期: 2024-04-18
- 刊出日期: 2025-03-19

Dynamic Global Reliability Assessment of 500kV Tension Suspension-braced Transmission System

1.
School of Civil Engineering, Chongqing University, Shapingba District, Chongqing 400045, China
2.
School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, Heilongjiang Province, China
3.
China Electric Power Research Institute, Xicheng District, Beijing 100055, China
4.
School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, Heilongjiang Province, China

Funds:

Science and Technology Project of State Grid Corporation of China 5200-202156071A-0-0-00

Chongqing Municipal National Natural Science Foundation CSTB2024NSCQ-MSX1134

Chongqing Natural Science Foundation-Innovation Development Joint Foundation Project CSTB2023NSCQ-LZX0080

摘要

摘要: 作为适用于山区地形的新型输电体系，500 kV耐张型悬索支撑输电体系为典型的风敏感结构且可能存在多个失效模式，开展其在随机风荷载作用下的动力整体可靠度研究以评估该耦联系统安全性尤为重要。为此，该文建立耐张型悬索支撑输电体系动力整体可靠性分析框架。首先，发展该新型输电体系在随机风荷载作用下的非线性有限元模型；然后，考察耐张型悬索支撑输电体系存在的各类张力失效模式；进而，基于状态变量描述法建立耐张型悬索支撑输电体系整体失效模式的单一等价功能函数；最后，通过广义概率密度演化理论开展耐张型悬索支撑输电体系动力整体可靠性分析。结果表明：输电导线和支撑导线悬索的归一化张力极值概率密度函数均为非规则曲线，且分别呈现出右偏分布和左偏分布趋势；输电导线和支撑导线悬索的张力极值分别主要集中在60~90 kN和300~400 kN区间，其对应的动力可靠度分别为0.965 7和1；耐张型悬索支撑输电体系动力整体可靠度与输电导线张力失效模式下的动力可靠度一致，其将随着结构阻尼的减小而降低。结果可为耐张型悬索支撑输电体系抗风整体可靠性设计及工程实践提供一定参考。
- 悬索支撑输电体系 /
- 多失效模式 /
- 随机风荷载 /
- 概率密度演化方法 /
- 动力整体可靠度
Abstract: As a new type of transmission structure suitable for hilly terrain, the 500 kV tension suspension-braced transmission system is a typical wind sensitive structure and may have multiple failure modes. Therefore, it is particularly important to analyze its dynamic global reliability under the stochastic wind load to evaluate the safety of the coupled system. In this regard, a framework is established for the dynamic global reliability analysis of the tension suspension-braced transmission system. First, a nonlinear finite element model considering the stochastic wind load effect is developed for the new transmission system. Then, various tension failure modes of the tension suspension-braced transmission system are investigated, and the equivalent performance function for the global failure mode of the tension type suspension support transmission system is described uniformly by the state variable description method. Finally, the dynamic global reliability of the tension suspension-braced transmission system is analyzed by using the probability density evolution method. The example results show that: 1) The probability density functions of the maximum normalized tension of the conductor and the supporting-conductor suspension cable are both irregular curves, showing trends of right-skewed distribution and left-skewed distribution, respectively. 2) The maximum tension for the conductor and the supporting-conductor suspension cable are mainly concentrated in the range of 60~90 kN and 300~400 kN, respectively, with corresponding dynamic reliability values of 0.965 7 and 1. 3) The global dynamic reliability of the tension suspension-braced transmission structure is consistent with the dynamic reliability of the conductor in the tension failure mode, which would decrease with the decrease of structural damping. These findings can provide useful references for the globe reliability design of wind-resistance and engineering practice of the tension suspension-braced transmission system.
- suspension-braced transmission system /
- multiple failure modes /
- stochastic wind load /
- probability density evolution method /
- dynamic global reliability

HTML全文

0. 引言

电力系统是保障社会经济持续发展的重要生命线工程，随着高压输电工程持续推进，山区输电线路建设发展迅速。目前，承载输电线路的输电塔在结构形式上主要分为自立式输电塔^[1-4]和拉线式输电塔^[5-6]2种类型。自立式输电塔在大跨度和特高压输电体系领域中应用广泛，但在山区地形中，其塔位选择往往较为困难。拉线式输电塔占地面积较大，常应用于戈壁荒漠等地区，其受地形限制难以适用于山区地貌。因此，电力行业开始研究与山区高压输电工程需求相符的新型输电体系。塔位选择不受山区地貌限制的500 kV耐张型悬索支撑输电体系^[7]为一种具有跨度大、结构高柔等特点的新型架空输电体系，其为典型的风敏感结构。现有研究^[7-9]针对耐张型悬索支撑输电体系所处风场特性、力学模型、风振响应分析和风致疲劳损伤评估等方面开展较为系统的研究，分析发现耐张型悬索支撑输电体系风振响应受所处风场脉动风成分和结构几何非线性的影响较为显著。

值得指出的是，上述有关耐张型悬索支撑输电体系的研究均在确定性动力分析的框架下展开研究。然而，由于脉动风荷载具有显著的随机性，其将致使耐张型悬索支撑输电体系风振响应亦具有随机特性；同时，由于耐张型悬索支撑输电体系为输电线-支撑悬索-耐张绝缘子串耦联系统，其可能存在多个失效模式，需同时考虑动力效应和多失效模式的影响，也即需要开展随机风荷载作用下耐张型悬索支撑输电体系动力整体可靠性评估。由于耦联系统组成的耐张型悬索支撑输电体系具有较强的几何非线性，其在随机风荷载作用下的动力整体可靠性评估为典型的非线性系统动力整体可靠性分析问题。基于概率守恒原理发展而来的概率密度演化法^[10]因具有不受非线性程度限制和分析效率较高等优势而为开展随机风荷载作用下耐张型悬索支撑输电体系动力整体可靠性评估提供一种行之有效的思路。但值得说明的是，由于概率密度演化法依赖于对随机空间的概率剖分，该方法对高维随机问题仍然具有挑战性。然而，广泛被用于脉动随机风场模拟的谱表示方法^[11-12]包含上千个随机变量，其为典型的高维随机问题。因此，引入高效的随机风场降维方法并结合概率密度演化理论进行耐张型悬索支撑输电体系动力整体可靠度评估成为另一重要任务。

为此，本文结合非线性有限元理论和仅用1或2个基本随机变量构造正交随机函数以模拟随机脉动风速场的谱表示-随机函数方法，建立耐张型悬索支撑输电体系在随机风荷载作用下的非线性动力分析模型；进而，考察耐张型悬索支撑输电体系存在的各类张力失效模式，并建立整体失效模式下的单一等价功能函数；最后，基于广义概率密度演化理论，开展耐张型悬索支撑输电体系动力整体可靠性分析。

1. 随机风荷载作用下的耐张型悬索支撑输电体系非线性有限元模型

1.1 简化力学模型

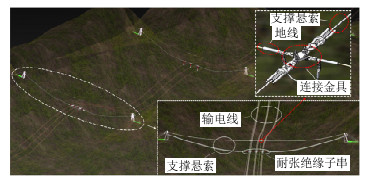
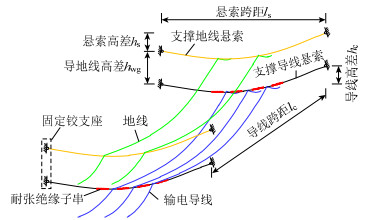
如图 1所示，500 kV耐张型悬索支撑输电体系主要由输电线、支撑悬索和耐张绝缘子串等组成，其简化力学模型如图 2所示。该输电体系的结构参数含义如下：h_s和l_s分别为同一跨支撑悬索两端边界点之间的垂直距离和水平距离；h_c和l_c分别为同一跨输电线相邻2个悬挂点之间的垂直距离和水平距离；h_wg为支撑地线悬索与支撑导线悬索相邻端点之间的垂直距离。输电线与支撑悬索的连接处均为金具连接的节点，可简化为耦合节点，输电导线为四分裂导线，根据面积相等原理将其等效为单根导线^[13]，在动力整体可靠性分析中则以单根子导线的受力性能进行研究。就耐张型悬索支撑输电体系边界条件而言，由于固定支架尺寸远小于支撑悬索跨距，固定于边界支架上的支撑悬索端部可处理为固定铰支座，与边界支撑悬索相连接的输电线边界处亦处理为固定铰支座。

图 1 500 kV耐张型悬索支撑输电体系及其组成

Figure 1. 500 kV tension suspension-braced transmission system and its components

下载: 全尺寸图片幻灯片

图 2 简化力学模型

Figure 2. Simplified mechanical model

下载: 全尺寸图片幻灯片

耐张型悬索支撑输电体系中，支撑悬索和输电线在自重作用下的初始形状可基于抛物线方程进行确定^[14]：

$y = 4{l_x}{f_{{\text{sag}}}}(1 - {l_x}/{l_{{\text{cs}}}})/{l_{{\text{cs}}}}$

(1)

${f_{{\text{sag}}}} = ql_{{\text{cs}}}^2/(8{H_{s}})$

(2)

式中：y和l_x分别为计算点垂直坐标和水平坐标；l_cs为跨距；f_sag为弧垂；q为单位长度上的重力荷载；H_s为张力的水平分量。

在顺风向风致动力分析中，可主要考虑耐张型悬索支撑输电体系抗拉强度^[7]。同时，考虑到新型输电体系风振属于大变形小应变问题，其有限元模型可采用三维杆单元建立。根据文献[7]，该输电体系的单元刚度矩阵K_e、质量矩阵M_e和阻尼矩阵C_e分别为：

$\boldsymbol{K}_{\mathrm{e}}=\frac{E A \varepsilon}{l}\left[\begin{array}{cc} \boldsymbol{I}_{3 \times 3} & -\boldsymbol{I}_{3 \times 3} \\ -\boldsymbol{I}_{3 \times 3} & \boldsymbol{I}_{3 \times 3} \end{array}\right]+\frac{E A}{l^3}\left[\begin{array}{cc} \boldsymbol{a}_{\mathrm{e}} \boldsymbol{a}_{\mathrm{e}}^{\mathrm{T}} & -\boldsymbol{a}_{\mathrm{e}} \boldsymbol{a}_{\mathrm{e}}^{\mathrm{T}} \\ -\boldsymbol{a}_{\mathrm{e}} \boldsymbol{a}_{\mathrm{e}}^{\mathrm{T}} & \boldsymbol{a}_{\mathrm{e}} \boldsymbol{a}_{\mathrm{e}}^{\mathrm{T}} \end{array}\right]$

(3)

$\boldsymbol{M}_{\mathrm{e}}=\frac{\rho A l_0}{6}\left[\begin{array}{cc} 2 \boldsymbol{I}_{3 \times 3} & \boldsymbol{I}_{3 \times 3} \\ \boldsymbol{I}_{3 \times 3} & 2 \boldsymbol{I}_{3 \times 3} \end{array}\right]$

(4)

$\boldsymbol{C}_{\mathrm{e}}=\alpha_{\mathrm{v}} \boldsymbol{M}_{\mathrm{e}}+\beta_{\mathrm{v}} \boldsymbol{K}_{\mathrm{e}}$

(5)

式中：ε=(l−l₀)/l₀，为单元应变；E为弹性模量；A为截面面积；l₀和l分别为初始和变形后单元长度；I_3×3为3阶单位矩阵；a_e为变形后单元向量；ρ为密度；α_v和β_v是Rayleigh阻尼常数，可取β_v=0^[15]。

1.2 随机风荷载

随机风速可考虑为平均风速和随机脉动风速2部分，对于平均风速，本文采用平均风速剖面指数律^[16]：

${\bar V_z} = {\bar V_{10}}{(z/10)^\alpha }$

(6)

式中： ${\bar V_z}$ 和 ${\bar V_{10}}$ 分别为z高度处和10 m高度处平均风速；α为地面粗糙度系数。

随机脉动风速模拟方法采用谱表示-随机函数方法^[17]，其可极大地减少随机变量数量，并有效地提高随机脉动风模拟效率。第j个模拟点的随机脉动风速V_j(t)(j=1, 2, ···, n)考虑为零均值平稳随机过程，计算式为

$\begin{array}{l} {V_j}(t) \approx 2\sum\limits_{k = 1}^j {\sum\limits_{m = 1}^N {\sqrt {\Delta \omega } {H_{jk}}({\omega _{km}})({R_{km}}\cos {\omega _{km}}t} } - \hfill \\ ~~~~~~~~~~~~ {\text{ }}{I_{km}}\sin {\omega _{km}}t) \hfill \\ \end{array}$

(7)

式中：Δω为频率间隔；H_jk(ω)为经Cholesky分解所得的互功率谱密度矩阵元素；N为频率截断项数；ω_km为双索引频率，ω_km=(m−1+k/n)Δω；{R_km, I_km}为零均值的实正交随机变量集，k=1, 2, ···, n；m=1, 2, ···, N。由于{R_km, I_km}仅需满足正交性条件，可假设一组正交随机变量集 $\{ {\bar R_{rs}},{\bar I_{rs}}\}$ (r=1, 2, ···, n；s=1, 2, ···, N)：

$\left\{ \begin{gathered} {{\bar R}_{rs}} = \sqrt 2 \cos (r{\mathit{\Theta} _1} + {\alpha _r}) \times \sin (s{\mathit{\Theta} _2} + {\beta _r}) \\ {{\bar I}_{rs}} = \sqrt 2 \sin (r{\mathit{\Theta} _1} + {\alpha _r}) \times \cos (s{\mathit{\Theta} _2} + {\beta _r}) \\ \end{gathered} \right.$

(8)

式中：Θ₁和Θ₂为相互独立且均服从(0, 2π)上均匀分布的基本随机变量；α_r和β_r是区间上的2个任意确定性参数，均可取为π/4。通过确定性的一一映射关系将 $\{ {\bar R_{rs}},{\bar I_{rs}}\}$ 转换为{R_km, I_km}，即 ${\bar R_{rs}} \to$ R_km和 ${\bar I_{rs}} \to$ I_km。

对于式(8)中的基本随机变量{Θ₁, Θ₂}，本文采用基于点集GF-偏差最小的点集优选策略^[18]在区间(0, 1)×(0, 1)上选取均匀离散的代表性样本点集 $\{ {\vartheta _{1l}},{\vartheta _{2l}}\}$ (l=1, 2, ···, n_sel)，同时计算代表性样本点的赋得概率P_l，且总赋得概率为1。区间(0, 1)×(0, 1)内的样本 $\{ {\vartheta _{1l}},{\vartheta _{2l}}\}$ 可通过线性变换映射到区间(0, 2π)× (0, 2π)上，从而获得基本随机变量{Θ₁, Θ₂}的代表性样本点集{θ_1l, θ_2l}，且原赋得概率P_l保持不变。

由式(7)和(8)可得，各模拟点的随机脉动风速V_Θ(t)。耐张型悬索支撑输电体系随机风荷载计算式为

$F_D(\boldsymbol{\varTheta})=\frac{1}{2} \rho_{\mathrm{air}} V(\boldsymbol{\varTheta})^2 C_{\mathrm{D}} A_{\mathrm{p}}$

(9)

式中：F_D(Θ)为单位长度上随机风荷载；ρ_air为空气密度；Θ为风速中的随机因素；V(Θ)为随机风速，V(Θ)= ${\bar V_z}$ +V_Θ(t)；C_D为体型系数；A_p为单位长度上的迎风面积。

1.3 非线性动力有限元模型

在随机风荷载作用下，基于更新Lagrange列式的耐张型悬索支撑输电体系非线性动力方程可表示为

$\boldsymbol{M} \ddot{\boldsymbol{u}}(\boldsymbol{\varTheta})_{t+\Delta t}+\boldsymbol{C} \dot{\boldsymbol{u}}(\boldsymbol{\varTheta})_{t+\Delta t}+\boldsymbol{Q}(\boldsymbol{\varTheta})_{t+\Delta t}=\boldsymbol{F}(\boldsymbol{\varTheta})_{t+\Delta t}$

(10)

式中：M和C分别为整体质量矩阵和整体阻尼矩阵，由单元特性矩阵M_e和C_e组集得到；下标“t+Δt”表示时刻； ${\ddot{\boldsymbol{u}}}{({\boldsymbol{\varTheta }})_{t + \Delta t}}$ 和 ${\dot{\boldsymbol{u}}}{({\boldsymbol{\varTheta }})_{t + \Delta t}}$ 分别为整体加速度向量和整体速度向量；Q(Θ)_t+Δt为整体抗力向量；F(Θ)_t+Δt为由随机风荷载等效的整体节点荷载向量。

当Δt时间内位移增量较小时，式(10)可改写为

$\begin{aligned} & M \ddot{\boldsymbol{u}}(\boldsymbol{\varTheta})_{t+\Delta t}+ \boldsymbol{C} \dot{\boldsymbol{u}}(\boldsymbol{\varTheta})_{t+\Delta t}+\boldsymbol{K}_t \Delta \boldsymbol{u}(\boldsymbol{\varTheta})= \\ &~~~~~~~~~~~~~~~~~~~~~~~~ \boldsymbol{F}(\boldsymbol{\varTheta})_{t+\Delta t}-\boldsymbol{Q}(\boldsymbol{\varTheta})_t \end{aligned}$

(11)

式中：K_tΔu(Θ)=Q(Θ)_t+Δt−Q(Θ)_t；K_t为t时刻整体刚度矩阵，由K_e组集得到；Δu(Θ)为Δt内的体系位移增量，Δu(Θ)=u(Θ)_t+Δt−u(Θ)_t。式(11)为非线性有限元方程，为保证结果准确性，本文采用结合Newton-Raphson法的Newmark-β法进行求解。

2. 耐张型悬索支撑输电体系动力整体可靠性分析方法

2.1 耐张型悬索支撑输电体系的多失效模式

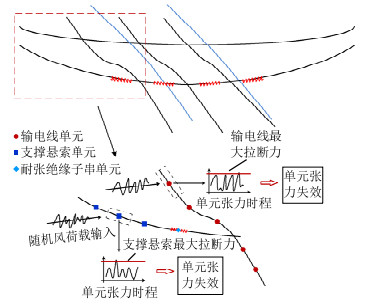
在随机风荷载作用下，输电线张力、支撑悬索张力和耐张绝缘子串张力可能超过对应的最大拉断力，即发生张力失效破坏，耐张型悬索支撑输电体系不再满足既定功能需求，即可认为其发生破坏。如图 3所示，在有限元动力分析中，耐张型悬索支撑输电体系被离散为各类单元，各单元张力均可能超过其最大拉断力而发生张力失效破坏。

图 3 单元张力失效

Figure 3. Tension failure mode of elements

下载: 全尺寸图片幻灯片

当t∈[0, T]时，基于强度理论，随机风荷载作用下输电线第i个单元张力失效模式可表示为

${f_{1,i}}:{b_1} - {T_{1,i}}({\boldsymbol{\varTheta }},t) < 0,{\text{ }}i = 1,2, \cdots ,{N_1}$

(12)

式中：b₁为输电线对应的最大拉断力；T_{1, i}(Θ, t)为输电线第i个单元张力，其可以通过本构关系及变形协调关系等由u(Θ)_t和 ${\boldsymbol{\dot u}}{({\boldsymbol{\varTheta }})_t}$ 求得；N₁为输电线单元数量。

类似地，支撑悬索第j个单元张力失效模式可表示为

${f_{2,j}}:{b_2} - {T_{2,j}}({\boldsymbol{\varTheta }},t) < 0,{\text{ }}j = 1,2, \cdots ,{N_2}$

(13)

式中：b₂为支撑悬索对应的最大拉断力；T_{2, j}(Θ, t)为支撑悬索第j个单元张力；N₂为支撑悬索单元数量。

耐张绝缘子串第k个单元张力失效模式为

${f_{3,k}}:{b_3} - {T_{3,k}}({\boldsymbol{\varTheta }},t) < 0,{\text{ }}k = 1,2, \cdots ,{N_3}$

(14)

式中：b₃为耐张绝缘子串对应的最大拉断力；T_{3, k}(Θ, t)为耐张绝缘子串第k个单元张力；N₃为耐张绝缘子串单元数量。

2.2 耐张型悬索支撑输电体系的单一等价功能函数

在上述分析的基础上，耐张型悬索支撑输电体系输电线、支撑悬索和耐张绝缘子串单元张力失效的功能函数可归一化表示为

${g_i}({\boldsymbol{\varTheta }},t) = 1 - \frac{{{T_i}({\boldsymbol{\varTheta }},t)}}{{{b_i}}} < 0,{\text{ }}i = 1,2, \cdots ,{N_\text{e}}$

(15)

式中：b_i为i单元对应的最大拉断力；T_i(Θ, t)为i单元张力；N_e为单元数量。

基于状态变量描述法^[19-20]，可建立耐张型悬索支撑输电体系整体失效的单一等价功能函数：

$Z = \mathop {\min }\limits_{i = 1,2, \cdots ,{N_\text{e}}} \{ \mathop {\min }\limits_{t \in [0,T]} [{g_i}({\boldsymbol{\varTheta }},t)]\}$

(16)

2.3 基于广义概率密度演化理论的动力整体可靠度分析方法

在获得耐张型悬索支撑输电体系整体失效的单一等价功能函数后，其动力整体可靠度可表示为

$\begin{gathered} R = \Pr \{ Z > 0\} = \Pr \{ \mathop {\min }\limits_{i = 1,2, \cdots ,{N_\text{e}}} \{ \mathop {\min }\limits_{t \in [0,T]} [1 - \frac{{{T_i}({\boldsymbol{\varTheta }},t)}}{{{b_i}}}]\} > 0\} = \hfill \\ {\text{ }}\Pr \{ 1 - \frac{1}{{{b_i}}}\mathop {\max }\limits_{i = 1,2, \cdots ,{N_\text{e}}} \{ \mathop {\max }\limits_{t \in [0,T]} [{T_i}({\boldsymbol{\varTheta }},t)]\} > 0\} \hfill \\ \end{gathered}$

(17)

记 ${X_{\max }}({\boldsymbol{\varTheta }}) = \mathop {\max }\limits_{i = 1,2, \cdots ,{N_\text{e}}} \{ \mathop {\max }\limits_{t \in [0,T]} [{T_i}({\boldsymbol{\varTheta }},t)]\} /{b_i}$ ，则耐张型悬索支撑输电体系动力整体可靠度为

$R = \Pr \{ 1 - {X_{\max }}({\boldsymbol{\varTheta }}) > 0\} = \int_{ - \infty }^1 {{p_{{X_{\max }}}}({x_{\max }})\text{d}{x_{\max }}}$

(18)

式中 ${p_{{X_{\max }}}}({x_{\max }})$ 为X_max(Θ)的概率密度函数。

进而，构造如下虚拟随机过程：

${X_{\text{vir}}}({\boldsymbol{\varTheta }},\tau ) = {X_{\max }}({\boldsymbol{\varTheta }})\sin (\frac{{\mathsf{π }}}{2}\tau ),{\text{ }}\tau \in [0,1]$

(19)

广义概率密度演化方程^[10]如下：

$\frac{\partial p_{X_{\mathrm{vir}} \boldsymbol{\varTheta }}\left(x_{\mathrm{vir}}, \boldsymbol{\theta}, \tau\right)}{\partial \tau}+\dot{X}_{\mathrm{vir}}(\boldsymbol{\theta}, \tau) \frac{\partial p_{X_{\mathrm{vir}} \boldsymbol{\varTheta }}\left(x_{\mathrm{vir}}, \boldsymbol{\theta}, \tau\right)}{\partial x_{\mathrm{vir}}}=0$

(20)

式中 ${p_{{X_{\mathrm{vir}}}{\boldsymbol{\varTheta }}}}({x_{\mathrm{vir}}},{\boldsymbol{\theta}},\tau )$ 为t时刻增广系统(X_vir(Θ, τ), Θ)的联合概率密度函数。

式(20)的初始条件为

${p_{{X_{{\text{vir}}}}{\boldsymbol{\varTheta }}}}({x_{{\text{vir}}}},{\boldsymbol{\theta}},\tau ){|_{\tau = 0}} = \delta ({x_{{\text{vir}}}} - {x_0}){p_{\boldsymbol{\varTheta }}}({\boldsymbol{\theta}})$

(21)

式中：δ(·)为Dirac函数；x₀为X_vir(Θ, τ)的初值。

由于X_max(Θ)的概率密度函数等价于τ=1时刻的X_vir(Θ, τ)概率密度分布，因此可采用有限差分格式通过求解式(20)获得X_max(Θ)的概率密度函数，即：

${p_{{X_{\max }}}}({x_{\max }}) = {p_{{X_{{\text{vir}}}}}}({x_{{\text{vir}}}},\tau ){|_{\tau = 1}}$

(22)

3. 算例分析

3.1 算例概述

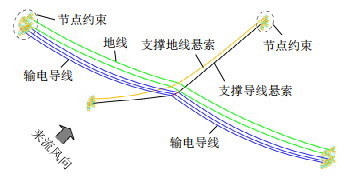
采用上述动力分析方法建立随机风荷载作用下耐张型悬索支撑输电体系的两跨模型，来流风向垂直于输电线路走向，如图 4所示。该输电体系支撑导线悬索端部的固定点位于距地面300 m高度处，结构参数如下：l_s=600 m、l_c=400 m、h_wg=20 m、h_s=0 m和h_c=0 m。由于耐张型悬索支撑输电体系处于山区地貌，其来流风场可按B类风剖面考虑，地面粗糙系数α取为0.15，基本风速^[21]取为27.5 m/s (重现期100年)。另外，输电导线型号为JLG1A- 400/35，支撑导线悬索型号为JG3A-767，地线型号选用JLB20A-120，支撑地线悬索型号选用JG3A- 240，输电线、支撑导线悬索和耐张绝缘子串的材料特性见表 1。

图 4 体系有限元模型和来流风向

Figure 4. Finite element model of the system and the wind direction

下载: 全尺寸图片幻灯片

表 1 材料特性

Table 1. Material characteristics

参数	输电导线	支撑导线悬索	地线	耐张绝缘子串
截面积/mm²	425.24	766.5	121.21	—
直径/mm	26.82	36	14.25	330
单位长度重量/(kg/m)	1.35	6.07	0.81	10
弹性模量/(N/mm²)	6.5×10⁴	1.8×10⁵	1.47×10⁵	2×10⁵
额定拉断力/kN	103.7	1 165.1	152.73	530

下载: 导出CSV

| 显示表格

3.2 随机风速样本

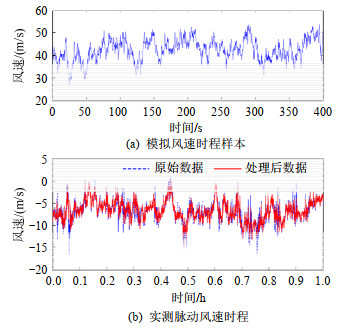
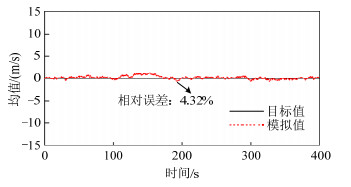
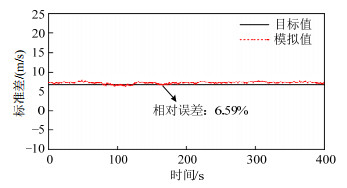
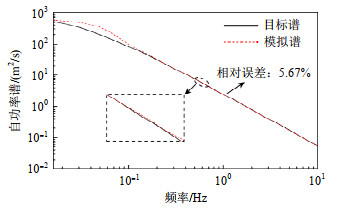
本算例中，脉动风速自功率谱采用Kaimal风速谱^[22]，空间相干性则依据Davenport相干函数模型^[23]进行计算，Davenport相干函数的衰减系数按文献[24]取值，表 2为模拟脉动风场的参数。输电导线跨中位置处的风速代表性样本时程(第200条)如图 5(a)所示，另外，图 5(b)给出山区地形中的实测脉动风速时程^[25]。可以看出，模拟风速与实测脉动风速的波形较为接近，表明代表性样本时程模拟结果具有脉动风速时程的特征。500条输电导线跨中位置处脉动风速样本的均值相对误差、标准差相对误差与自功率谱相对误差^[26]如表 3所示，相对误差均较小。图 6、7分别为500条输电导线跨中位置处脉动风速代表性样本时程的均值与目标值、标准差与目标值比较，目标均值和目标标准差如表 2所示，可以看出，均值、标准差结果均与目标值较为接近。500条脉动风速代表性样本的自功率谱与目标谱比较如图 8所示，脉动风速代表性样本集合的自功率谱与目标谱拟合基本一致。

表 2 脉动风场模拟参数

Table 2. Parameters for simulating the fluctuating wind field

计算参数	取值	计算参数	取值
截断频率/(rad/s)	4π	样本数量n_sel	500
频率离散点数	1 200	地面粗糙长度/m	0.03
频率间隔/(rad/s)	4π/1 200	X方向衰减系数	8
持时/s	400	Y方向衰减系数	16
时间步长/s	0.01	Z方向衰减系数	10
目标均值/(m/s)	0	目标标准差/(m/s)	6.77

下载: 导出CSV

| 显示表格

图 5 风速代表性样本

Figure 5. Representative samples of wind speed

下载: 全尺寸图片幻灯片

表 3 风场模拟精度

Table 3. Simulation accuracy of the wind field

计算参数	均值相对误差/%	标准差相对误差/%	自功率谱相对误差/%
模拟值	4.32	6.59	5.67
目标值	—	—	—

下载: 导出CSV

| 显示表格

图 6 均值与目标值

Figure 6. Simulated mean values and target value

下载: 全尺寸图片幻灯片

图 7 标准差与目标值

Figure 7. Simulated standard deviations and target value

下载: 全尺寸图片幻灯片

图 8 自功率谱与目标谱

Figure 8. Simulated auto-power spectrums and target spectrum

下载: 全尺寸图片幻灯片

3.3 耐张型悬索支撑输电体系随机风振响应分析

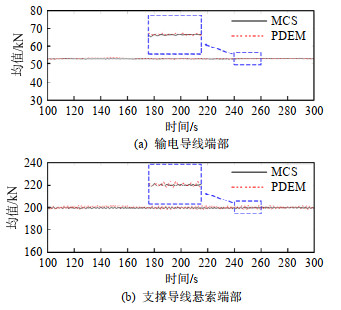
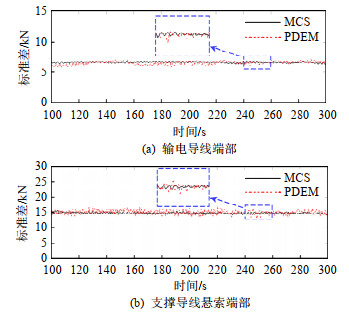
在对两跨耐张型悬索支撑输电体系进行500次确定性时程分析的基础上，本文采用广义概率密度演化理论进行耐张型悬索支撑输电体系随机风振响应分析。同时，按照蒙特卡洛模拟方法(Monte Carlo simulation，MCS)进行3 000次确定性时程分析，将计算得到的响应结果与概率密度演化方法(probability density evolution method，PDEM)计算结果进行对比，以输电导线端部、支撑导线悬索张力为例，100~300 s内的对比结果如图 9和10所示，整个计算期内两者的响应结果二范数相对误差如表 4所示。可以发现，PDEM结果在MCS结果附近波动，其与MCS结果的二范数相对误差最大为4.12%，在可接受范围之内。

图 9 张力均值

Figure 9. Mean value of the tension

下载: 全尺寸图片幻灯片

图 10 张力标准差

Figure 10. Standard deviation of the tension

下载: 全尺寸图片幻灯片

表 4 PDEM与MCS的结果比较

Table 4. Comparison of results between PDEM and MCS

计算方法	样本数量	均值二范数相对误差/%		标准差二范数相对误差/%
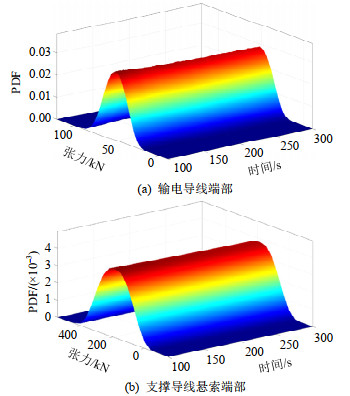
计算方法	样本数量	输电导线	支撑导线悬索	输电导线	支撑导线悬索
PDEM	500	0.68	0.48	4.04	4.12
MCS	3 000	—	—	—	—

下载: 导出CSV

| 显示表格

图 11给出100~300 s内的输电导线、支撑导线悬索端部张力的概率密度曲面，其向底面投影可得到概率密度等值线，如图 12所示。不难发现，随着时间变化，输电导线端部张力的等概率密度线呈现出较大的波动，其中，中部的等概率密度线逐渐由平行状态演化为重合状态，而支撑导线悬索端部张力的等概率密度线则无明显变化。表明输电导线端部张力受随机风荷载影响较为明显，而支撑导线悬索端部张力受随机风荷载影响较小。

图 11 张力概率密度演化曲面

Figure 11. Probability density evolution surface of the tension

下载: 全尺寸图片幻灯片

图 12 张力等概率密度线

Figure 12. Contour of the probability density evolution surface for the tension

下载: 全尺寸图片幻灯片

同时，通过随机动力响应分析结果可知，支撑导线悬索端部张力最大值为427.74 kN，未超过支撑导线悬索张力阈值，输电导线端部张力最大值为116.27 kN，而输电导线张力阈值为103.7 kN。因此，耐张型悬索支撑输电体系的输电导线部分在随机风荷载作用下可能会出现风振破坏的情况。

3.4 耐张型悬索支撑输电体系动力整体可靠度分析

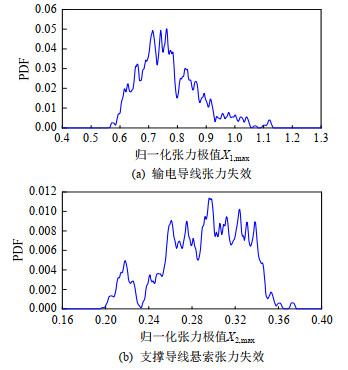
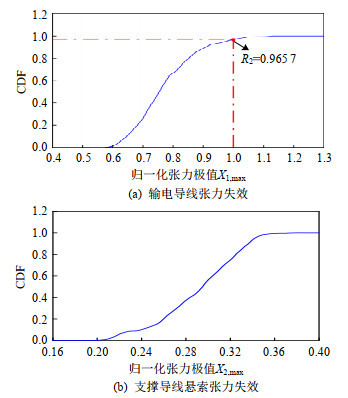
通过式(17)—(22)，可计算耐张型悬索支撑输电体系动力整体可靠度。类似地，亦可通过广义概率密度演化理论分别计算输电导线张力失效模式下和支撑导线悬索张力失效模式下的动力可靠度，其中，支撑导线悬索张力失效模式包括支撑导线悬索单元张力失效和耐张绝缘子串单元张力失效。输电导线张力失效模式和支撑导线悬索张力失效模式下的归一化张力极值变量分别为X_{1, max}和X_{2, max}，其概率密度函数(probability density function，PDF)如图 13所示，相应的累积分布函数(cumulative distribution function，CDF)如图 14所示。可以看出，输电导线归一化张力极值主要分布在0.58~0.87区间内，即输电导线最大张力主要分布在60~90 kN区间，其概率密度函数趋于右偏分布，而支撑导线悬索归一化张力极值主要分布在0.26~0.35，即支撑导线悬索最大张力主要分布在300~400 kN区间，其概率密度函数呈现出左偏分布趋势。输电导线最大拉断力为103.7 kN，在输电导线张力失效模式下，计算得到动力可靠度为0.965 7，对于支撑导线悬索而言，其张力阈值为支撑导线悬索最大拉断力，即为1 165.1 kN，在支撑导线悬索张力失效模式下，计算得到动力可靠度为1。

图 13 不同失效模式下的等价极值变量PDF

Figure 13. PDF of the equivalent extreme variables under different failure modes

下载: 全尺寸图片幻灯片

图 14 不同失效模式下的等价极值变量CDF

Figure 14. CDF of the equivalent extreme variables under different failure modes

下载: 全尺寸图片幻灯片

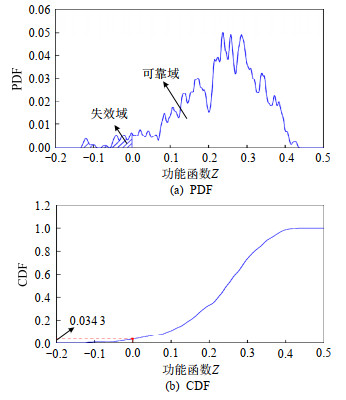
耐张型悬索支撑输电体系整体失效的单一等价功能函数Z的PDF和CDF如图 15所示。由图 15(a)可知，单一等价功能函数Z主要分布在0.1~0.4区间，显然，该两跨耐张型悬索支撑输电体系张力水平在大多数情况下处于安全范围内。由图 15(b)可得，耐张型悬索支撑输电体系动力整体可靠度R=1−0.034 3=0.965 7，显然，其与输电导线张力失效模式下的动力可靠度一致，表明该耦联系统的失效由输电导线控制。

图 15 整体失效功能函数Z的PDF和CDF

Figure 15. PDF and CDF of performance function Z under the global failure

下载: 全尺寸图片幻灯片

3.5 阻尼对耐张型悬索支撑输电体系动力整体可靠度的影响

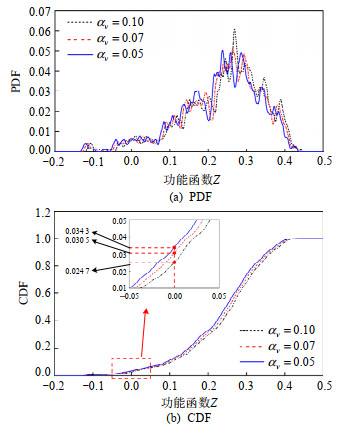
为评估阻尼对耐张型悬索支撑输电体系动力整体可靠度的影响，本文选取3种不同的α_v值(α_v=0.1、0.07和0.05)，其余参数取值不变，分别计算耐张型悬索支撑输电体系动力整体可靠度。不同阻尼工况下耐张型悬索支撑输电体系整体失效的单一等价功能函数Z的PDF和CDF如图 16所示。显然，随着结构阻尼的减小，功能函数Z的PDF和CDF曲线整体上呈现出向左偏移的趋势，其表明耐张型悬索支撑输电体系整体失效概率逐渐增大。经计算，α_v=0.1，α_v=0.07和α_v=0.05工况下耐张型悬索支撑输电体系动力整体可靠度分别为0.975 3、0.969 5和0.965 7。因此，随着阻尼减小，耐张型悬索支撑输电体系动力整体可靠度会逐渐降低。本文采用较小的阻尼，得到的耐张型悬索支撑输电体系动力整体可靠度亦较小，此为偏安全的结果。

图 16 不同阻尼工况下整体失效功能函数Z的PDF和CDF

Figure 16. PDF and CDF of performance function Z under the global failure under different damping cases

下载: 全尺寸图片幻灯片

4. 结论

耐张型悬索支撑输电体系是一类适用于山区地形的新型架空输电体系。本文结合谱表示-随机函数方法和非线性有限元理论，发展随机风荷载作用下耐张型悬索支撑输电体系的非线性有限元分析模型，进而采用状态变量描述法和广义概率密度演化理论，研究某两跨耐张型悬索支撑输电体系随机风振响应，并进行动力整体可靠度评估。得到主要结论如下：

1）基于概率密度演化理论得到的耐张型悬索支撑输电体系中输电导线和支撑导线悬索随机风振响应均值和标准差结果，与蒙特卡洛模拟均值和标准差结果拟合较好。

2）输电导线张力失效模式和支撑导线悬索张力失效模式下的动力可靠度分别为0.965 7和1，耐张型悬索支撑输电体系动力整体可靠度与输电导线张力失效模式下的动力可靠度一致，其表明该耦联系统的失效由输电导线控制。随着结构阻尼减小，耐张型悬索支撑输电体系动力整体可靠度会逐渐降低。

3）输电导线端部张力的概率分布为非规则曲线，而支撑导线悬索端部张力的概率分布曲线较为规则，相较于支撑导线悬索端部张力，输电导线端部张力受随机风荷载影响较为显著。

4）输电导线张力极值的概率密度函数趋于右偏分布，而支撑导线悬索张力极值的概率密度函数呈现出左偏分布趋势。

值得说明的是，尽管本文研究500 kV耐张型悬索支撑输电体系动力整体可靠性分析框架，但仍需深入研究与完善，如通过现场实测或风洞试验等方式获取耐张型悬索支撑输电体系所处风场和风致响应等数据，进而结合本文方法对耐张型悬索支撑输电体系开展更为细致和精确的动力整体可靠性分析。

图 1 500 kV耐张型悬索支撑输电体系及其组成

Figure 1. 500 kV tension suspension-braced transmission system and its components

下载: 全尺寸图片幻灯片

图 2 简化力学模型

Figure 2. Simplified mechanical model

下载: 全尺寸图片幻灯片

图 3 单元张力失效

Figure 3. Tension failure mode of elements

下载: 全尺寸图片幻灯片

图 4 体系有限元模型和来流风向

Figure 4. Finite element model of the system and the wind direction

下载: 全尺寸图片幻灯片

图 5 风速代表性样本

Figure 5. Representative samples of wind speed

下载: 全尺寸图片幻灯片

图 6 均值与目标值

Figure 6. Simulated mean values and target value

下载: 全尺寸图片幻灯片

图 7 标准差与目标值

Figure 7. Simulated standard deviations and target value

下载: 全尺寸图片幻灯片

图 8 自功率谱与目标谱

Figure 8. Simulated auto-power spectrums and target spectrum

下载: 全尺寸图片幻灯片

图 9 张力均值

Figure 9. Mean value of the tension

下载: 全尺寸图片幻灯片

图 10 张力标准差

Figure 10. Standard deviation of the tension

下载: 全尺寸图片幻灯片

图 11 张力概率密度演化曲面

Figure 11. Probability density evolution surface of the tension

下载: 全尺寸图片幻灯片

图 12 张力等概率密度线

Figure 12. Contour of the probability density evolution surface for the tension

下载: 全尺寸图片幻灯片

图 13 不同失效模式下的等价极值变量PDF

Figure 13. PDF of the equivalent extreme variables under different failure modes

下载: 全尺寸图片幻灯片

图 14 不同失效模式下的等价极值变量CDF

Figure 14. CDF of the equivalent extreme variables under different failure modes

下载: 全尺寸图片幻灯片

图 15 整体失效功能函数Z的PDF和CDF

Figure 15. PDF and CDF of performance function Z under the global failure

下载: 全尺寸图片幻灯片

图 16 不同阻尼工况下整体失效功能函数Z的PDF和CDF

Figure 16. PDF and CDF of performance function Z under the global failure under different damping cases

下载: 全尺寸图片幻灯片

表 1 材料特性

Table 1 Material characteristics

参数	输电导线	支撑导线悬索	地线	耐张绝缘子串
截面积/mm²	425.24	766.5	121.21	—
直径/mm	26.82	36	14.25	330
单位长度重量/(kg/m)	1.35	6.07	0.81	10
弹性模量/(N/mm²)	6.5×10⁴	1.8×10⁵	1.47×10⁵	2×10⁵
额定拉断力/kN	103.7	1 165.1	152.73	530

下载: 导出CSV

表 2 脉动风场模拟参数

Table 2 Parameters for simulating the fluctuating wind field

计算参数	取值	计算参数	取值
截断频率/(rad/s)	4π	样本数量n_sel	500
频率离散点数	1 200	地面粗糙长度/m	0.03
频率间隔/(rad/s)	4π/1 200	X方向衰减系数	8
持时/s	400	Y方向衰减系数	16
时间步长/s	0.01	Z方向衰减系数	10
目标均值/(m/s)	0	目标标准差/(m/s)	6.77

下载: 导出CSV

表 3 风场模拟精度

Table 3 Simulation accuracy of the wind field

计算参数	均值相对误差/%	标准差相对误差/%	自功率谱相对误差/%
模拟值	4.32	6.59	5.67
目标值	—	—	—

下载: 导出CSV

表 4 PDEM与MCS的结果比较

Table 4 Comparison of results between PDEM and MCS

计算方法	样本数量	均值二范数相对误差/%		标准差二范数相对误差/%
计算方法	样本数量	输电导线	支撑导线悬索	输电导线	支撑导线悬索
PDEM	500	0.68	0.48	4.04	4.12
MCS	3 000	—	—	—	—

下载: 导出CSV

参考文献(26)

[1]	邵帅, 杨风利, 程永锋, 等. 大跨越输电高塔发展历程及其结构承载性能研究综述[J]. 中国电机工程学报, 2022, 42(S1): 313-331. DOI: 10.13334/j.0258-8013.pcsee.221479 SHAO Shuai, YANG Fengli, CHENG Yongfeng, et al. Development of long-span high-rise transmission towers and research on structural bearing capacity: a review[J]. Proceedings of the CSEE, 2022, 42(S1): 313-331(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.221479
[2]	杨风利, 李清华, 邵帅, 等. 脱冰工况下特高压输电铁塔地线横担受力特征及破坏模式[J]. 中国电机工程学报, 2024, 44(10): 4157-4166. DOI: 10.13334/j.0258-8013.pcsee.230141 YANG Fengli, LI Qinghua, SHAO Shuai, et al. Mechanical characteristics and destroyed modes for cross-arm supporting ground wires of UHV transmission tower under ice shedding[J]. Proceedings of the CSEE, 2024, 44(10): 4157-4166(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.230141
[3]	何浩林, 汪大海, 黄增浩, 等. 输电直线杆塔风灾易损性的准静态分析方法[J]. 中国电机工程学报, 2024, 44(9): 3732-3741. DOI: 10.13334/j.0258-8013.pcsee.222189 HE Haolin, WANG Dahai, HUANG Zenghao, et al. Wind hazard fragility analysis of transmission free-standing towers using quasi-static method [J]. Proceedings of the CSEE, 2024, 44(9): 3732-3741(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.222189
[4]	李正良, 肖正直, 韩枫, 等. 1 000 kV汉江大跨越特高压输电塔线体系气动弹性模型的设计与风洞试验[J]. 电网技术, 2008, 32(12): 1-5. LI Zhengliang, XIAO Zhengzhi, HAN Feng, et al. Aeroelastic model design and wind tunnel tests of 1000kV Hanjiang long span transmission line system[J]. Power System Technology, 2008, 32(12): 1-5(in Chinese).
[5]	俞登科, 李正良, 施菁华, 等. ±800 kV直流双柱悬索拉线塔塔线体系风振响应的风洞试验研究[J]. 中国电机工程学报, 2015, 35(4): 1009-1013. DOI: 10.13334/j.0258-8013.pcsee.2015.04.031 YU Dengke, LI Zhengliang, SHI Jinghua, et al. Wind tunnel test on wind-induced response of ±800 kV DC cross-rope suspension tower-line[J]. Proceedings of the CSEE, 2015, 35(4): 1009-1013(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.2015.04.031
[6]	李正良, 张智航, 王涛. 考虑多重性能水准的特高压双柱悬索拉线塔风灾易损性分析[J]. 中国电机工程学报, 2024, 44(20): 8304-8315. DOI: 10.13334/j.0258-8013.pcsee.231261 LI Zhengliang, ZHANG Zhihang, WANG Tao. Wind fragility analysis of UHV double column suspended guyed tower considering multiple performance levels[J]. Proceedings of the CSEE, 2024, 44(20): 8304-8315(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.231261
[7]	李正良, 王邦杰, 王涛. 考虑山地风场效应的耐张型悬索支撑输电结构风振响应分析[J/OL]. 工程力学, 2023[2023-10-26]. http://kns.cnki.net/kcms/detail/11.2595. O3.20230821.1823.006. html. LI Zhengliang, WANG Bangjie, WANG Tao. Wind- induced vibration response of tension suspension-braced transmission structure in hilly terrain[J/OL]. Engineering Mechanics, 2023[2023-10-26]. http://kns.cnki.net/kcms/detail/11.2595.O3.20230821.1823.006.html(in Chinese).
[8]	李正良, 王邦杰, 王涛. 考虑施扰山体影响的耐张型悬索支撑输电结构风振疲劳损伤分析[J]. 振动工程学报, 2025, 38(2): 279-291. LI Zhengliang, WANG Bangjie, WANG Tao. Wind-induced fatigue damage analysis of the tension suspension- braced transmission structure considering the effect of occluding hills[J]. Journal of Vibration Engineering, 2025, 38(2): 279-291(in Chinese).
[9]	王涛, 王邦杰, 李正良. 考虑连续山体影响的耐张型悬索支撑输电结构风振响应分析[C]//第32届全国结构工程学术会议论文集(第Ⅱ册). 赣州: 2023. WANG Tao, WANG Bangjie, LI Zhengliang. Wind-induced vibration response of the tension suspension-braced transmission structure considering the influence of consecutive hills[C]//Proceedings of the 32th National Academic Conference on Structural Engineering (Volume Ⅱ). Ganzhou: 2023(in Chinese).
[10]	LI Jie, CHEN Jianbing. Stochastic dynamics of structures [M]. Singapore: John Wiley & Sons (Aisa) Pet Ltd, 2010.
[11]	SHINOZUKA M. Monte Carlo solution of structural dynamics[J]. Computers & Structures, 1972, 2(5-6): 855-874.
[12]	DEODATIS G. Simulation of ergodic multivariate stochastic processes[J]. Journal of Engineering Mechanics, 1996, 122(8): 778-787.
[13]	汪大海, 韩少鸿, 黄国庆, 等. 输电线路龙卷风风振响应的参数分析[J]. 高电压技术, 2022, 48(10): 3871-3881. WANG Dahai, HAN Shaohong, HUANG Guoqing, et al. Parametric analysis for dynamic response of transmission lines under tornado[J]. High Voltage Engineering, 2022, 48(10): 3871-3881(in Chinese).
[14]	楼文娟, 张跃龙, 徐海巍. 考虑冰风耦合作用的输电导线脱冰动张力及参数影响分析[J]. 高电压技术, 2022, 48(3): 1052-1059. LOU Wenjuan, ZHANG Yuelong, XU Haiwei. Dynamic tension following ice shedding and parameters' influence analysis of transmission conductor considering the coupling effect of ice and wind[J]. High Voltage Engineering, 2022, 48(3): 1052-1059(in Chinese).
[15]	吴茂田. 悬索结构的风致动力效应分析[D]. 重庆: 重庆大学, 2010. WU Maotian. Research on the wind-induced vibration of cable structure[D]. Chongqing: Chongqing University, 2010(in Chinese).
[16]	中华人民共和国住房和城乡建设部. 建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Architecture & Building Press, 2012(in Chinese).
[17]	LIU Zhangjun, LIU Zenghui. Random function representation of stationary stochastic vector processes for probability density evolution analysis of wind-induced structures[J]. Mechanical Systems and Signal Processing, 2018, 106: 511-525.
[18]	CHEN Jianbing, YANG Junyi, LI Jie. A GF-discrepancy for point selection in stochastic seismic response analysis of structures with uncertain parameters[J]. Structural Safety, 2016, 59: 20-31.
[19]	CHEN Jianbing, LI Jie. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters[J]. Structural Safety, 2007, 29(2): 77-93.
[20]	SONG Pengyan, WANG Tao, LU Dagang. Structural global reliability assessment considering nonlinear correlation effects by enhanced high-order moment method[J]. Acta Mechanica Sinica, 2023, 39(4): 722356.
[21]	交通运输部. 公路桥梁抗风设计规范: JTG/T 3360-01— 2018[S]. 北京: 人民交通出版社, 2018. Ministry of Transport of the People's Republic of China. Wind-resistant design specification for highway bridges: JTG/T 3360-01—2018[S]. Beijing: China Communications Press, 2018(in Chinese).
[22]	KAIMAL J C, WYNGAARD J C, IZUMI Y, et al. Spectral characteristics of surface-layer turbulence[J]. Quarterly Journal of the Royal Meteorological Society, 1972, 98(417): 563-589.
[23]	DAVENPORT A G. The spectrum of horizontal gustiness near the ground in high winds[J]. Quarterly Journal of the Royal Meteorological Society, 1961, 87(372): 194-211.
[24]	武岳, 孙瑛, 郑朝荣, 等. 风工程与结构抗风设计[M]. 哈尔滨: 哈尔滨工业大学出版社, 2019: 40-41. WU Yue, SUN Ying, ZHENG Chaorong, et al. Wind engineering and wind-resistant design of structures[M]. Harbin: Harbin Institute of Technology Press, 2019: 40-41(in Chinese).
[25]	ZHANG Jinxiang, ZHANG Minglin, LI Yongle, et al. Comparison of wind characteristics in different directions of deep-cut gorges based on field measurements[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2021, 212: 104595.
[26]	LIU Zhangjun, LIU Zixin, CHEN Denghong. Probability density evolution of a nonlinear concrete gravity dam subjected to nonstationary seismic ground motion[J]. Journal of Engineering Mechanics, 2018, 144(1): 04017157.