N−k Multi-stage Bi-level Optimization and Fault Scenario Screening Model of Power System Considering Cascading Failure Propagation Path
-
摘要: 当前电力系统通过经典N−k安全分析直接筛选危害最大的k重预想事故场景时，忽略了源发故障带来的故障动态传播过程，导致N−k安全分析结果偏保守。因此，该文重点刻画故障传播过程中系统拓扑规模与连接关系的变化，建立计及连锁故障传播路径的N−k多阶段双层优化及故障场景筛选模型；其中上层以负荷损失最大为目标，筛选k重源发故障及其故障传播路径，下层以负荷损失最小为目标，模拟调度中心调整发电机出力、负荷大小等抑制故障级联传播的过程。引入对偶变量将该双层模型转化为单层模型进行求解，然而，对偶变量的引入会产生非线性项，存在收敛速度慢的问题。所以，该文提出一种两阶段网络流算法，以得到对偶变量上下界从而消除引入的非线性项，同时缩小模型可行域，快速求解该文模型。仿真结果表明：所提方法能有效辨识高危N−k源发故障场景及多阶段故障传播路径且求解速度提升12倍。Abstract: The current power system directly screens for the most hazardous k-level predicted accident scenarios through classical N−k security analysis, neglecting the dynamic propagation process of faults caused by source faults, leading to conservative N−k security analysis results. Therefore, this paper focuses on characterizing the changes in system topology scale and connection relationships during fault propagation, and establishes an N−k multi-stage bi-level and fault scenario screening model considering cascading failure propagation path. The upper layer aims at the maximum load loss, screening k-level source faults, and identifying its failure propagation paths. The lower layer, aiming at the minimum load loss, simulates the process of suppressing the cascading propagation of faults by adjusting generator output and load size. The dual variables are introduced to transform the bi-level model into a single-layer model as a solution. However, the multiplication of dual variables will produce nonlinear terms, resulting in slow convergence speed. Therefore, this paper proposes a two-stage network flow algorithm, which can obtain upper and lower bounds of the dual variables, thereby eliminating the nonlinear terms and reducing the model feasible region, and then solves the proposed model quickly. Finally, the simulation results verify that the method can effectively identify high-risk N−k source fault scenarios and multi-stage fault propagation paths, and the solving speed is increased by 12 times.
-
0. 引言
近年来，全球大停电事故的频繁发生给电力系统的安全稳定运行带来了极大威胁[1-3]。2019年阿根廷大停电、2020年墨西哥大停电等多起大停电事故表明，系统中多个元件故障会引发连锁故障，产生大量孤岛区域导致系统解列，给系统造成重大停电损失[4-5]。因此，开展考虑连锁故障过程的N−k安全性研究，给电力系统规划人员提供决策依据，对预防系统大停电事故发生具有重要意义。
通常采用枚举法[6]、状态采样[7]、双层规划理论[8]等方法对电力系统进行N−k安全分析。枚举法实现简单，但该方法计算成本高，如在仅含100个元件的系统中，N−3安全分析要进行1.6×105次仿真[9]。因此，为避免枚举法带来的巨大计算量，依托于智能算法缩减搜索空间的N−k安全分析方法受到广泛关注，通过构建特征指标如潮流分布因子、线路风险值、电压波动等，依托于随机响应面法[10]、图注意力网络算法[11]、数据挖掘技术[12]，筛选高风险N−k预想事故集。这类研究虽能通过刻画事故发生概率或构建关键性指标缩减搜索空间提升求解效率，但无法保证其为全局最优解，安全分析结果偏片面[13]。
此外，有学者基于双层规划理论，通过建立N−k双层优化模型在避免枚举法巨大计算量的同时，从全局进行N−k安全分析[14-15]，其中上层筛选对系统造成负荷损失最大的k重源发故障，下层调整发电机出力、负荷大小以最小化负荷损失，但忽略了故障级联传播过程，安全分析结果偏保守。因此，部分学者改进上层模型，考虑每个故障阶段仅由单一故障组成，进行多阶段N−k安全分析[16-17]，但忽略了连锁故障存在多个元件故障的可能。也有学者通过多个N−k双层优化模型解耦分析源发故障阶段和级联传播阶段[18]，但解耦分析未考虑到各个故障阶段存在因果关系。且上述研究为保证双层优化模型的可行性，只能筛选不会引发系统解列的源发故障场景。然而，连锁故障快速传播最终易导致系统解列[19]。因此，实现含连锁故障过程的全局N−k安全分析是个难点问题。
采用对偶理论求解N−k双层优化模型是目前主流方法[14-18]，但会引入大量对偶变量和产生非线性项，降低求解效率，难以实现模型在大规模系统中的应用。综上所述，如何从全局分析角度刻画连锁故障传播过程，筛选高危事故集，并保证双层优化模型求解中的可行性和计算效率，是现代电力系统N−k安全分析的重要科学问题。
因此，本文重点刻画源发故障阶段、级联传播阶段和优化调度阶段下系统拓扑规模、连接关系和运行状态的变化，在此基础上建立计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型，然后，通过两阶段网络流算法快速求解本文模型，辨识能够引发连锁故障的高危N−k源发故障场景及多阶段故障传播路径，有效预防大停电事故的发生。
1. 计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型框架
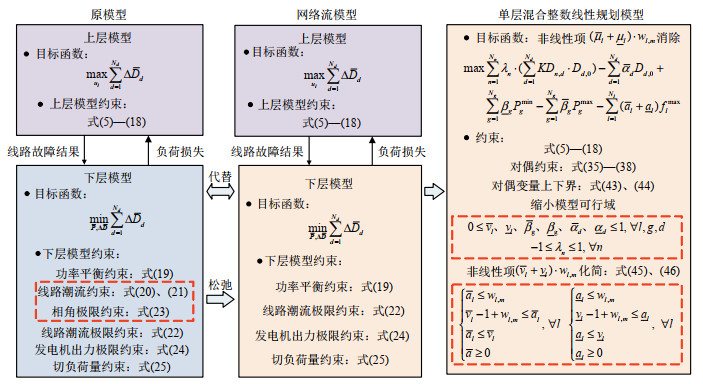
本文针对k重源发故障带来的连锁反应，通过建立计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型，实现高危N−k源发故障场景及多阶段故障传播路径辨识，模型框架如图 1所示。将连锁故障传播分为源发故障阶段、级联传播阶段与优化调度阶段[20]。
![]()
图 1 计及连锁故障的电力系统N−k多阶段双层优化及故障场景筛选模型框架Figure 1. N−k bi-level screening model framework of power system considering cascading failure1）源发故障阶段。
假设系统中有Nl条线路，在源发故障阶段任意选择k条线路触发其故障，从系统中退出运行，记为N−k源发故障场景，如式(1)所示。
$$ S = \{ {l_0}|{u_{{l_0}}} = 0\} $$ (1) 式中：ul为0-1变量，表示线路l在源发故障阶段是否故障，取1表示未故障，取0表示故障；S为k重源发故障集合，集合元素l0为ul取0时的源发故障线路编号。
2）级联传播第s阶段。
k重源发故障发生后会引发潮流转移，系统其余元件可能因过载跳闸，往复循环，从而形成连锁故障持续传播[21-22]。在级联传播阶段，系统中元件相继退出运行会导致系统拓扑规模与连接关系发生改变。同时大量线路断开，系统可能会出现孤岛，导致孤岛功率和主网功率不平衡，违反节点功率平衡约束，潮流计算难以收敛。所以，如何解决孤岛问题带来的模型不可解问题也是本文研究重点。
因此，在级联传播阶段，主要进行系统拓扑规模与连接关系更新以及孤岛处理，然后基于直流潮流判断在该阶段是否有线路过载跳闸，直到调度中心进行优化调度。由于直流潮流被广泛应用于预想事故集筛选中[13, 20]。所以，本文采用直流潮流模型进行级联传播阶段的潮流计算。
在每个级联传播阶段，判断线路、发电机、负荷等元件是否正常运行，继而判断该元件是否从系统中断开，更新系统拓扑规模与连接关系。基于更新后的系统拓扑进行潮流计算，判断在该阶段是否有其他元件l因承载功率超过其热稳定极限而过载跳闸，如果是，则该类元件退出运行，记入级联传播第s阶段的故障线路集Qs，如式(2)所示。
$$ {Q_s} = \{ {l_s}|{e_{{l_s},s}} = 1\} ,{\text{ }}\forall s $$ (2) 式中：el, s为0-1变量，表示线路l在级联传播第s阶段是否过载跳闸，取1表示过载跳闸，取0表示未过载；集合元素ls为el, s取1时，在级联传播第s阶段发生故障的线路编号。
3）优化调度阶段。
调度中心根据故障级联传播后系统的运行状态，以负荷损失最小为目标进行优化调度，并记录负荷大小、涵盖源发故障阶段和级联传播阶段的故障线路集S、Qs，记作多阶段故障传播路径L。
$$ \boldsymbol{L}: \boldsymbol{S} \rightarrow \boldsymbol{Q}_1 \rightarrow \boldsymbol{Q}_2 \rightarrow \cdots \rightarrow \boldsymbol{Q}_s $$ (3) 4）迭代与筛选。
重复步骤1）—3）得到所有k重源发故障组合对系统造成的负荷损失，筛选得到对系统造成危害最大的N−k源发故障场景及多阶段故障传播路径。
5）计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型建模及求解。
为避免遍历所有故障组合带来的巨大计算量，将上述计及连锁故障的N−k安全分析过程转化为一个双层混合整数规划问题，其中上层模型包括源发故障阶段和级联传播阶段，以k重源发故障发生后对系统造成的负荷损失最大为目标，筛选能够引发连锁故障并对系统危害最大的N−k源发故障场景；同时，通过在上层模型中添加线路运行状态、发电机运行状态和负荷运行状态变化约束以及孤岛处理约束，对系统拓扑规模与连接关系进行更新和提高模型的可行性计算，具体建模见2.2和2.3节。下层则根据上层提供的线路故障结果，以负荷损失最小为目标实现发电机出力、负荷的最优调整。上层则根据下层系统运行模拟结果对k重源发故障最终造成的负荷损失进行统计。其中模型涉及的所有变量及公式统一说明见文献[23]。
最后，提出一种两阶段网络流算法快速求解本文模型，先通过网络流模型代替下层的最优直流潮流模型，得到对偶变量的上下界和消除非线性项，然后通过对偶理论将模型转化为单层混合整数线性规划模型，采用求解器Gurobi求解，当式(4)取得最优值时，得到对系统危害最大的N-k源发故障场景及多阶段故障传播路径。
$$ \max\limits _{u_l} \min\limits _{\overline{\boldsymbol{P}}, \Delta \overline{\boldsymbol{D}}} \sum\limits_{d=1}^{N_d} \Delta \bar{D}_d $$ (4) 式中：ul为上层模型的决策变量；$ \overline{\boldsymbol{P}} $、$ \Delta \overline{\boldsymbol{D}} $为下层模型的决策变量；Nd为系统中负荷节点数量；$ \overline{\boldsymbol{P}} $为下层发电机出力矩阵，其中，元素$ {\bar P_g} $为下层发电机g出力；$ \Delta \overline{\boldsymbol{D}} $为负荷损失矩阵，其中，元素$ \Delta {\bar D_d} $为下层负荷节点d的负荷损失。
2. 计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型建模
2.1 计及连锁故障的上层优化模型
在源发故障阶段，系统中只有k条线路故障。考虑到在电力系统中发生三阶以上的源发故障概率很低[24]。因此，仿真计算中，k一般小于等于3。
$$ \sum\limits_{l = 1}^{{N_l}} {(1 - {u_l}) = k} $$ (5) 式中：Nl为系统中线路数量；k为源发故障数量。
在源发故障阶段除源发故障外，其余线路均保持正常运行，如式(6)所示。
$$ {w_{l,0}} = {u_l}{\text{, }}\forall l $$ (6) 式中wl, 0为0-1变量，表示线路l在源发故障阶段运行状态，取1表示正常运行，取0表示断开。
对于任一节点n，在级联传播第s阶段需满足节点功率平衡约束，如式(7)所示。
$$ \boldsymbol{K}_{\mathrm{L}} \cdot \boldsymbol{F}_s=\boldsymbol{K}_{\mathrm{P}} \cdot \boldsymbol{P}_s-\boldsymbol{K}_{\mathrm{D}} \cdot \boldsymbol{D}_s, \quad \forall s $$ (7) 式中：KL为节点-线路矩阵，其中，元素KLn, l取1表示节点n与线路l相连，且连接方向为离开节点n，取−1表示连接方向为指向节点n，取0表示未相连；KP为节点-发电机矩阵，其中，元素KPn, g取1表示节点n与发电机g相连，取0表示未相连。KD为节点-负荷矩阵，其中，元素KDn, d取1表示节点n与负荷d相连，取0表示未相连；Fs为级联传播第s阶段的线路潮流矩阵，其中，元素fl, s为级联传播第s阶段的线路l潮流，具体计算如式(8)所示；Ps为级联传播第s阶段的发电机出力矩阵，其中，元素Pg, s为级联传播第s阶段的发电机g出力，具体计算如式(14)所示；Ds为级联传播第s阶段的负荷矩阵，其中，元素Dd, s为级联传播第s阶段的负荷节点d负荷，具体计算如式(16)所示。
对于任一线路l，通过式(8)计算其在级联传播第s阶段的线路潮流。
$$ \boldsymbol{F}_s=\boldsymbol{B}_s \boldsymbol{\theta}_s, \quad \forall s $$ (8) 式中：Bs为级联传播第s阶段的线路-节点导纳矩阵，其中，元素bl, s为级联传播第s阶段的线路l导纳，具体计算见式(10)；θs为级联传播第s阶段的相角矩阵，其中，元素θn, s为级联传播第s阶段的节点n相角。
对于任一线路l，通过式(9)判断其在级联传播第s阶段是否过载跳闸。
$$ {e_{l,s}} = \left\{ \begin{gathered} 1,{\text{ }}{f_{l,s}} \geqslant f_l^{\max } \hfill \\ 0,{\text{ }}{f_{l,s}} \lt f_l^{\max } \hfill \\ \end{gathered} \right.{\text{, }}\forall l,s $$ (9) 式中$ f_l^{\max } $为线路l最大传输容量。
2.2 连锁故障系统拓扑规模与连接关系更新约束
2.2.1 连锁故障中线路运行状态变化约束
在保证节点-线路矩阵KL和线路-节点导纳矩阵Bs维度不变的前提下，在任一级联传播第s阶段通过前一故障阶段线路l的运行状态wl, s−1对式(10)中的线路-节点导纳矩阵Bs中的元素bl, s进行更新，从而模拟线路l在系统中运行状态的变化。
当线路l从系统断开，则线路l的线路导纳bl, s为0，线路l潮流fl, s为0；反之，线路l的线路导纳bl, s保持不变，正常计算线路l潮流，如式(10)、(11)所示，其中式(10)为线路导纳bl, s更新，式(11)为级联传播第s阶段的线路l潮流fl, s计算。
$$ {b_{l,s}} = {b_l} \cdot {w_{l,s - 1}}{\text{, }}\forall l,s $$ (10) 式中wl, s为0-1变量，表示线路l在级联传播第s阶段的运行状态，取1为正常运行，取0为断开。
$$ {f_{l,s}} = - {b_{l,s}}\sum\limits_{n = 1}^{{N_n}} {K{L_{n,l}}{\theta _{n,s}}} {\text{, }}\forall l,s $$ (11) 由多起大停电事件可知，多元件故障往往是因极端事件而导致的永久性故障，且连锁故障传播过程中的线路故障也都为永久性故障[25]。因此，在整个故障阶段中，任何线路最多只改变一次运行状态，表示如下。
$$ {w_{l,s}} = {w_{l,s - 1}} - {e_{l,s}}{\text{, }}\forall l,s $$ (12) 2.2.2 连锁故障中发电机运行状态变化约束
大量线路退出运行，可能会导致发电机g从系统中断开。如果在级联传播第s阶段，与发电机g连接的所有线路都断开，则发电机g从系统中断开；反之，发电机g保持正常运行。
$$ \alpha_{g, s}=\left\{\begin{array}{ll} 0, & \sum\limits_{l \in E(g)} w_{l, s-1}=0 \\ 1, & \text { 其他 } \end{array}, \quad \forall g, s\right. $$ (13) 式中：E(g)为与发电机g连接的所有线路集合；0-1变量αg, s表示发电机g的运行状态，取1表示正常运行，取0表示断开。
通过αg, s控制发电机g的输出功率，模拟发电机g是否从系统中断开。若发电机g从系统中断开，则其输出功率Pg, s为0；反之，发电机g保持初始功率Pg, 0运行，如式(14)所示。
$$ {P_{g,s}} = {\alpha _{g,s}} \cdot {P_{g,0}}{\text{, }}\forall g,s $$ (14) 式中Pg, 0为发电机g的初始出力。
2.2.3 连锁故障中负荷运行状态变化约束
同样地，大量线路退出运行也可能会导致负荷d从系统中断开。如果在级联传播第s阶段与负荷d连接的所有线路都断开，则负荷d从系统中断开；反之，负荷d保持正常运行。
$$ \beta_{d, s}=\left\{\begin{array}{ll} 0, & \sum\limits_{l \in E(d)} w_{l, s-1}=0 \\ 1, & \text { 其他 } \end{array}, \quad \forall d, s\right. $$ (15) 式中E(d)为与负荷d连接的所有线路集合。
通过βd, s控制负荷d的功率，模拟负荷d是否从系统中断开。若负荷d从系统中断开，则其功率Dd, s为0；反之，负荷d保持初始功率Dd, 0运行，如式(16)所示。
$$ {D_{d,s}} = {\beta _{d,s}} \cdot {D_{d,0}},{\text{ }}\forall d,s $$ (16) 式中Dd, 0为负荷节点d的初始负荷功率。
2.3 连锁故障中孤岛处理
孤立节点其本身的输入功率和输出功率不相等会违反式(7)，通过式(13)—(16)将孤立节点的输入功率和输出功率同时置零，不仅能模拟该节点从系统中断开，也能保证该孤立节点功率平衡。
此外，当发电机或负荷从系统中断开时，不仅会导致其节点本身功率不平衡，也会使得系统内剩余发电机的输出功率和负荷功率不相等，导致系统内剩余节点的输入功率和输出功率不平衡，违反式(7)。因此，通过调节平衡节点的功率保证即使发电机或者负荷从系统中断开，每个级联传播阶段系统功率仍能保持平衡，如式(17)、(18)所示。
$$ P_{n, s}=\boldsymbol{K}_{\mathrm{P}} \cdot \boldsymbol{P}_s-\boldsymbol{K}_{\mathrm{D}} \cdot \boldsymbol{D}_s, \quad \forall n \notin \bar{n}, s $$ (17) $$ {P_{\bar n,s}} = - \sum\limits_{n \ne \bar n} {{P_{n,s}}} {\text{, }}\forall s $$ (18) 式中：Pn, s为系统非平衡节点的节点n功率；$ {P_{\bar n,s}} $为系统平衡节点$ \bar n $的功率，为其余节点的节点功率之和。
2.4 基于负荷损失最小的下层优化调度模型
如图 1所示，下层采用最优直流潮流模型模拟调度部门对连锁故障的最优调整。
1）节点功率平衡约束。
$$ \boldsymbol{K}_{\mathrm{L}} \cdot \overline{\boldsymbol{f}}=\boldsymbol{K}_{\mathrm{P}} \cdot \overline{\boldsymbol{P}}-\boldsymbol{K}_{\mathrm{D}} \cdot\left(\boldsymbol{D}_0-\Delta \overline{\boldsymbol{D}}\right) $$ (19) 式中：$ \overline{\boldsymbol{f}} $为下层的线路潮流矩阵，其中，元素$ {\bar f_l} $为下层线路l潮流；D0为初始负荷矩阵，其中，元素Dd, 0为负荷d的初始负荷。
2）线路潮流约束。
$$ {\overline{f}}_{l}\le -{b}_{l}\cdot {\displaystyle \sum _{n=1}^{{N}_{n}}K{L}_{n,l}{\overline{\theta }}_{n}}\text{ }-\text{ 2}{\theta }^{\mathrm{max}}{b}_{l}（1-{w}_{l,m}\text{), }\forall l $$ (20) $$ {\overline{f}}_{l}\ge -{b}_{l}\cdot {\displaystyle \sum _{n=1}^{{N}_{n}}K{L}_{n,l}{\overline{\theta }}_{n}}\text{ + 2}{\theta }^{\mathrm{max}}{b}_{l}（1-{w}_{l,m}\text{), }\forall l $$ (21) 式中：$ {\bar \theta _n} $为下层节点n的相角；$ {\theta ^{\max }} $为节点n的最大相角。
3）线路潮流极限约束。
$$ - {w_{l,m}}f_l^{\max } \leqslant {\bar f_l} \leqslant {w_{l,m}}f_l^{\max }{\text{, }}\forall l $$ (22) 式中：m为故障级联传播次数；wl, m为级联传播第m阶段的线路运行状态。
4）相角极限约束。
$$ - \theta _{}^{\max } \leqslant {\bar \theta _n} \leqslant \theta _{}^{\max }{\text{, }}\forall n $$ (23) 5）发电机出力极限约束：
$$ P_g^{\min } \leqslant {\bar P_g} \leqslant P_g^{\max }{\text{, }}\forall g $$ (24) 式中$ P_g^{\max } $、$ P_g^{\min } $分别为发电机g出力上下限。
6）切负荷量约束。
$$ 0 \leqslant \Delta {\bar D_d} \leqslant {D_{d,0}}{\text{, }}\forall d $$ (25) 3. 基于两阶段网络流算法的双层模型求解
3.1 基于网络流模型的最优直流潮流模型近似
由式(19)—(25)可知，下层为线性规划问题，具有强对偶性。因此，可以利用对偶理论将 1 节所提的双层优化模型转化为单层混合整数规划模型进行求解。但直接利用对偶理论求解时，其目标函数式（26）因对偶变量 $\bar{v}_{l}、~ \underline{v}_{l}、~ \bar{\mu}_{l}、~ \underline{\mu}_{l}$ 的引入会出现非线性项 $\left(\bar{v}_{l}+\underline{v}_{l}\right) \cdot w_{l, m}$ 与 $\left(\bar{\mu}_{l}+\underline{\mu}_{l}\right) \cdot w_{l, m}$ 。由于对偶变量上界未知，无法直接对 $\left(\bar{v}_{l}+\underline{v}_{l}\right) \cdot w_{l, m}$ 和 $\left(\bar{\mu}_{l}+\underline{\mu}_{l}\right) \cdot w_{l, m}$ 线性化，只能通过大 M 法间接线性化。大 M 值足够大时才能保证模型的最优性。然而，大M值过大会极大增加模型计算时间[26]。
$$\begin{aligned} & \max \sum_{n=1}^{N_n} \lambda_n \cdot\left(\sum_{d=1}^{N_d} K D_{n, d} \cdot D_{d, 0}\right)-\sum_{d=1}^{N_d} \bar{\alpha}_d D_{d, 0}+ \\ & \sum_{g=1}^{N_g} \underline{\beta}_g P_g^{\min }-\sum_{g=1}^{N_g} \bar{\beta}_g P_g^{\max }-\sum_{l=1}^{N_l}\left(\bar{v}_l+\underline{v}_l\right) . \\ & w_{l, m} f_l^{\max }-\sum_{n=1}^{N_n} \theta_n^{\max }\left(\bar{\sigma}_n+\underline{\sigma}_n\right)+ \\ & 2 b_l \theta_{\max } \cdot\left(1-w_{l, m}\right)\left(\bar{\mu}_l+\underline{\mu}_l\right) \end{aligned}$$ (26) 式中 $\lambda_{n}、~ \bar{v}_{l}、~ \underline{v}_{l}、 ~ \bar{\beta}_{g}、 ~ \underline{\beta}_{g}、 ~ \bar{\alpha}_{d}、 ~ \underline{\alpha}_{d}、 ~ \bar{\sigma}_{n}、 ~ \underline{\sigma}_{n}、 ~$ $\bar{\mu}_{l}、 ~ \underline{\mu}_{l}$为对偶变量。
为解决多个非线性项和对偶变量的引入导致模型求解速度慢的问题，本文采用两阶段网络流算法求解本文模型，首先通过网络流模型近似下层的最优直流潮流模型，使得下层模型对偶问题的对偶变量系数矩阵为全幺模矩阵，继而得到对偶变量的上下界，从而缩小模型可行域和消除非线性项$\left(\bar{v}_{l}+\underline{v}_{l}\right) \cdot w_{l, m}$ 与 $\left(\bar{\mu}_{l}+\underline{\mu}_{l}\right) \cdot w_{l, m}$ ，以加快模型求解速度，再利用对偶理论将其转化为单层混合整数线性规划模型，最后，采用求解器Gurobi求解，其求解框架如图 2所示。
在最优直流潮流模型基础上松弛掉支路潮流约束式(20)、(21)和相角极限约束式(23)得到网络流模型，如下所示。
$$\min\limits _{\overline{\boldsymbol{P}}, \Delta \overline{\boldsymbol{D}}} \sum\limits_{d=1}^{N_d} \Delta \bar{D}_d$$ (27) $$ \boldsymbol{K} \boldsymbol{L} \cdot \overline{\boldsymbol{f}}=\boldsymbol{K} \boldsymbol{P} \cdot \overline{\boldsymbol{P}}-\boldsymbol{K} \boldsymbol{D} \cdot\left(\boldsymbol{D}_0-\Delta \overline{\boldsymbol{D}}\right) $$ (28) $$ - {w_{l,m}}f_l^{\max } \leqslant {\bar f_l} \leqslant {w_{l,m}}f_l^{\max }{\text{, }}\forall l $$ (29) $$ P_g^{\min } \leqslant {\bar P_g} \leqslant P_g^{\max }{\text{, }}\forall g $$ (30) $$ 0 \leqslant \Delta {D_d} \leqslant {D_{d,0}}{\text{, }}\forall d $$ (31) 定理1：根据复杂网络理论可知，电力系统可由有向图G(V, E)表示，其中：V表示节点集合，E表示线路集合。如果图G所有连通子图中线路的最大线路容量满足式(33)，则网络流模型的可行解u同时也是最优直流潮流模型的可行解[27]。
$$ R = \mathop {\max }\limits_{1 \leqslant i \leqslant t} \left| {{B^i}} \right| $$ (32) $$ \begin{gathered} f_l^{\max } \geqslant \sqrt {\frac{{{b_{l\max }}}}{{{b_{l\min }}}}} \frac{{\sqrt {R - 1} }}{2}{\left\| {{P_{g,0}} - {D_{d,0}}} \right\|_1}{\text{, }} \hfill \\ {\text{ }}\forall l \in \cup _{i = 1}^tE({B^i}),g,d \hfill \\ \end{gathered} $$ (33) 式中：Bi为图G中的连通子图；t为图G中连通子图的总个数；R为最大连通子图的顶点数；blmax、blmin分别为所有线路中的最大线路导纳和最小线路导纳。
根据定理1，本文可以用网络流模型近似代替下层的最优直流潮流模型。所提计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型重新表示如下，记为模型M1，如下所示。
式(4)
上层 s.t 式(5)—(18)
下层 s.t 式(28)—(31)
模型M1重新求对偶得到其对应的单层混合整数规划模型，记为模型M2，如下所示。
$$ \begin{aligned} & \max \sum_{n=1}^{N_n} \lambda_n \cdot\left(\sum_{d=1}^{N_d} K D_{n, d} \cdot D_{d, 0}\right)-\sum_{d=1}^{N_d} \bar{\alpha}_d D_{d, 0}+ \\ & \sum_{g=1}^{N_g} \underline{\beta}_g P_g^{\min }-\sum_{g=1}^{N_g} \bar{\beta}_g P_g^{\max }-\sum_{l=1}^{N_l}\left(\bar{v}_l+\underline{v}_l\right) \cdot w_{l, m} \cdot f_l^{\max } \end{aligned} $$ (34) s.t 式(5)—(18)
$$\sum\limits_{n=1}^{N_n}\left(K L_{n, l} \lambda_n\right)+\bar{v}_l-\underline{v}_l=0, \quad \forall l$$ (35) $$ \sum\limits_{n=1}^{N_n}\left(K P_{n, g} \lambda_n\right)-\bar{\beta}_g+\underline{\beta}_g=0, \quad \forall g$$ (36) $$ \sum\limits_{n=1}^{N_{n}}\left(K D_{n, d} \lambda_{n}\right)-\bar{\alpha}_{d}+\underline{\alpha}_{d}=1, \quad \forall d $$ (37) $$ \bar{v}_{l}、~ \underline{v}_{l}、~ \bar{\beta}_{g}、~ \underline{\beta}_{g}、~ \bar{\alpha}_{d}、~ \underline{\alpha}_{d} \geq 0, \quad \forall l, g, d $$ (38) 对比式(26)和(34)可知，通过网络流模型代替最优直流潮流模型，已将非线性项$\left(\bar{\mu}_{l}+\underline{\mu}_{l}\right) \cdot w_{l, m}$消除。下层采用网络流模型后，可以进一步得到对偶变量的上下界和消除非线性$\left(\bar{v}_{l}+\underline{v}_{l}\right) \cdot w_{l, m}$ ，具体流程如3.2节所示。
3.2 基于网络流模型的两阶段网络流算法求解
采用网络流模型后，从式(35)—(38)可知，模型M2对偶变量的系数矩阵为全幺模矩阵，由其行列式绝对值小于等于1的性质得到对偶变量上下界，同时消除非线性项$\left(\bar{v}_{l}+\underline{v}_{l}\right) \cdot w_{l, m}$，具体步骤如下。
用{x：Ax≤h}表示式(35)—(38)，其中：A为对偶变量的系数矩阵；x为对偶变量构成的矩阵。
通过克莱默法则计算对偶变量x得：
$$ \bar{x}_{i}=\left\{\operatorname{det}\left[\overline{\boldsymbol{A}}^{1} \overline{\boldsymbol{A}}^{2} \cdots \overline{\boldsymbol{A}}^{i-1} \boldsymbol{h} \overline{\boldsymbol{A}}^{i+1} \ldots \overline{\boldsymbol{A}}^{q}\right]\right\} /\{\operatorname{det}[\overline{\boldsymbol{A}}]\} $$ (39) 式中：$ {\bar A^i} $为A的子矩阵；q为对偶空间的维数。
因为A是一个整数矩阵，所以其子矩阵行列式的绝对值大于等于1，如式(40)所示。
$$ |\operatorname{det}[\overline{\boldsymbol{A}}]| \geq 1$$ (40) 根据式(39)和(40)得：
$$ \left|\bar{x}_{i}\right| \leq\left|\operatorname{det}\left[\overline{\boldsymbol{A}}^{1} \overline{\boldsymbol{A}}^{2} \cdots \overline{\boldsymbol{A}}^{i-1} \boldsymbol{h} \overline{\boldsymbol{A}}^{i+1} \cdots \overline{\boldsymbol{A}}^{q}\right]\right| $$ (41) 因为[A h]为全幺模矩阵，所以其行列式的绝对值小于等于1，如式(42)所示。
$$\left|\operatorname{det}\left[\bar{A}^1 \bar{A}^2 \cdots \bar{A}^{i-1} h \bar{A}^{i+1} \cdots \bar{A}^q\right]\right| \leq 1$$ (42) 则通过式(38)、(41)、(42)可求得所有对偶变量上下界，如式(43)、(44)所示。
$$ 0 \leq \bar{v}_l、\underline{v}、~ \bar{\beta}_{\mathrm{g}}、~ \underline{\beta}_{\mathrm{g}}、~ \bar{\alpha}_d、\underline{\alpha}_d \leq 1, \forall l, g, d $$ (43) $$ - 1 \leqslant {\lambda _n} \leqslant 1,{\text{ }}\forall n $$ (44) 得到对偶变量上下界后，可通过引入中间变量$\bar{a}_{l}、~ \underline{a}$ 将 $\bar{v}_{l} \cdot w_{l, m}$ 和 $\underline{v}_{l} \cdot w_{l, m}$线性化，如式(45)、(46)所示。
$$ \left\{\begin{array}{l} {{\bar a}_l} \leqslant {w_{l,m}} \hfill \\ {{\bar v}_l} - 1 + {w_{l,m}} \leqslant {{\bar a}_l} \hfill \\ {{\bar a}_l} \leqslant {{\bar v}_l} \hfill \\ \bar a \geqslant 0 \hfill \\ \end{array}\right.{\text{, }}\forall l $$ (45) $$ \left\{\begin{array}{l} \underline{a}_l \leq w_{l, m} \\ \underline{v}_l-1+w_{l, m} \leq \underline{a}_l, \quad \forall l \\ \underline{a}_l \leq \underline{v}_l \\ \underline{a}_l \geq 0 \end{array}\right. $$ (46) 由式(43)—(46)可知，利用网络流模型可进一步得到对偶变量上下界，同时将非性项$\left(\bar{v}_l+\underline{v}_l\right) \cdot w_{l, m}$消除。
所提计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型最终表示如下，记为模型M3：
$$\left\{\begin{aligned} & \max \sum_{n=1}^{N_n} \lambda_n \cdot\left(\sum_{d=1}^{N_d} K D_{n, d} \cdot D_{d, 0}\right)-\sum_{d=1}^{N_d} \bar{\alpha}_d D_{d, 0}+ \\ & \sum_{g=1}^{N_g} \underline{\beta}_g P_g^{\min }-\sum_{g=1}^{N_g} \bar{\beta}_g P_g^{\max }-\sum_{l=1}^{N_l}\left(\bar{a}_l+\underline{a}_l\right) f_l^{\max } \\ & \text { s.t. 式 }(5)-(18),(35)-(38),(45),(46) \end{aligned}\right.$$ (47) 指示函数式(9)、(13)、(15)，以式(9)为例采用大M法进行线性化[28-29]，如式(48)所示。
$$ \left\{\begin{array}{l} {f_{l,s}} - {f_{l,\max }} \leqslant M \cdot {e_l} - \varepsilon \hfill \\ {f_{l,s}} - {f_{l,\max }} \geqslant M \cdot ({e_l} - 1) \hfill \\ \end{array}\right. {\text{, }}\forall l,s $$ (48) 式中：M为一个极大的数；$ \varepsilon $为极小的数。
假设模型M3的最优解为z*，和取得最优解z*时的级联第m传播阶段线路运行状态为wl, m*。
由于网络流模型是在最优直流潮流模型基础上松弛后得到，所以将wl, m*固定到最优直流模型中所求得的负荷损失可能会大于网络流模型所求得的z*。因此，通过表 1所示步骤获得个更紧的上界。
表 1 基于两阶段网络流算法的高危源发N−k故障及多阶段传播路径辨辨识流程Table 1. High risk N−k fault identification process based on two-stage Flow network algorithm步骤 内容 步骤1 设置源发故障数量k和级联传播次数m 步骤2 根据所设置参数求解模型M3，根据式(47)得到最优解z*和级联传播第m阶段线路运行状态为wl, m* 步骤3 根据式(1)和(5)得到模型M3取得最优解z*时的k重源发故障集合S*，并输出。 步骤4 根据式(2)和(9)得到模型M3取得最优解z*时的级联传播第s阶段故障线路集Qs*并输出 步骤5 将wl, m*固定到最优直流潮流模型中，求解最优直流潮流模型式(4)、(19)—(25)，根据式(4)得到此时的负荷损失ΔD*输出 4. 算例分析
为验证本文模型的有效性，本节以IEEE39节点和IEEE118节点系统为例进行仿真验证，系统参数来自于matpower7.0软件包[30]。考虑到发电机出线断开会对系统造成较大冲击，现实中难以出现，且切除大量发电机会显著增加切负荷量，而相比于含发电机的升压变支路，普通输电线路的危害性难以直接辨识[31]。因此，本文只对含普通输电线路的源发故障进行辨识。所有仿真均在python中实现。
4.1 IEEE39节点系统高危N−k源发故障场景及多阶段故障传播路径辨识结果
由2.1节可知，源发故障数量k一般小于等于3，且在电力系统中会及时对故障进行阻断控制防止故障无限制传播[32]。因此，本文假设源发故障数量k从1增加到3，级联传播次数m设置为2，迭代求解本文模型次优解并按负荷损失大小进行排序，得到不同N−k场景下排名前3的结果N−k源发故障场景及其多阶段故障传播路径，如表 2所示。
表 2 IEEE39节点系统高危N−k源发故障场景及多阶段故障传播路径辨识结果Table 2. High risk N−k source fault scenario and multi-stage propagation path identification of IEEE39 bus systemk 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 42 3 1 503.7 32 — — 172 19 13 21 22 125.4 2 1 30 3 9 13 24 25 42 1 527.1 35 38 1 3 6 8 19 23 24 1 352.6 26 42 3 1 6 8 9 1 261 3 1 9 10 12 3 6 7 8 13 19 23 24 25 26 30 2 163.9 10 26 42 3 9 1 6 8 11 12 13 15 18 2 124.9 10 19 42 3 12 1 9 13 21 22 23 1 865.5 表 2为IEEE39节点系统不同N−k场景下排名前3的高危N−k源发故障场景及多阶段故障传播路径辨识结果。如k=1时，源发故障为线路42故障，故障蔓延到线路3和线路1，级联传播两次后所造成的负荷损失最大，为503.7 MW。
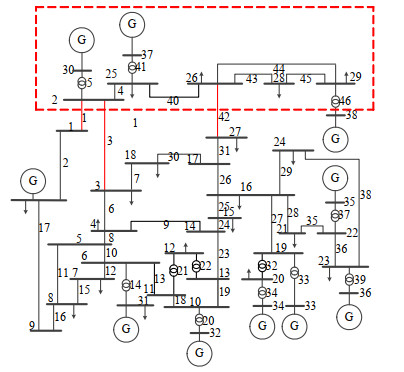
以N−1场景下排名第1的故障场景为例进行分析。在N−1场景下，线路42故障后，在级联传播阶段，先后导致线路3和线路1因过载跳闸，此时母线2、25、26、28、29、30、37、38所构成的子网络与系统解列，如图 3所示。正常运行时该区域的负荷量只有852.5MW，而发电功率为1 620 MW，解列后无法向其他网络中的负荷进行供电，调度只能减小该区域部分发电机出力和其他网络中的部分负荷。因此，线路42故障后造成的负荷损失最大为503.7 MW。
4.2 不同N−k源发故障场景辨识方法对比
文献[8]通过建立经典N−k模型对电力系统进行N−k安全分析，但经典N−k模型只考虑源发故障对系统的影响，并未考虑源发故障可能引发的多阶段故障级联传播过程对系统的影响，高危N−k源发故障场景的筛选结果偏保守。因此，为验证本文模型的有效性与准确性，将本文模型与经典N−k模型[8]进行对比，结果如表 3所示。
表 3 IEEE39节点系统不同模型对比结果Table 3. Comparison results of different models in IEEE39 bus systemk 模型 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 本文模型 42 3 1 503.7 经典N−k 32 — — 172 2 本文模型 1 30 3 9 13 24 25 42 1 527.1 经典N−k 35 38 — — 356.7 3 本文模型 1 9 10 12 3 6 7 8 13 19 23 24 25 26 30 2 163.9 经典N−k 1 11 12 — — 863.9 表 3为本文模型和经典N−k模型辨识出的危害最大的N−k源发故障场景结果。通过对比可知，相比于经典N−k模型，本文模型辨识出的N−k源发故障场景对系统造成的后果更为严重。如在N−2场景下，线路1和30发生故障后，因故障间的潮流转移相关性会导致陆续有6条线路断开，最终造成的负荷损失为1 527.1 MW，相比于经典N−k模型，负荷损失增加了328.12%。这是因为本文模型在源发故障发生后会引发连锁故障，导致故障蔓延。因此在考虑故障间协同破坏效应的情况下，源发故障发生后造成的协同后果会更为严重。
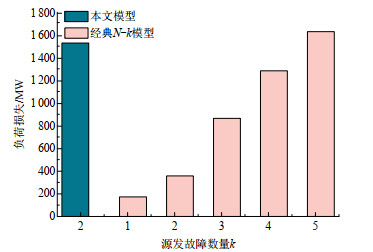
以本文模型的N−2场景为例，增加经典N−k模型中源发故障数量k进行仿真，直到经典N−k模型的负荷损失与本文模型在N−2场景中造成的负荷损失一致，结果如图 4所示。
![]()
图 4 N−2场景下IEEE39节点系统不同模型对比结果Figure 4. Comparison results of different models in IEEE39 bus system in N−2 scenario由图 4可知，本文模型在N−2场景下辨识出的源发故障对系统造成的负荷损失等价于经典N−k模型在N−5场景下对系统造成的负荷损失。然而，系统中5个元件同时故障的概率很低难以发生。所以，本文模型更适用于高阶N−k故障筛选。
4.3 IEEE39节点系统故障传播路径分析
4.3.1 IEEE39节点系统故障传播路径阻断分析
研究表明：级联传播阶段是抑制连锁故障继续传播的关键阶段[20]。因此，将辨识出的级联第一传播阶段故障线路进行阻断控制，在其恢复稳态前闭锁，避免因线路故障后的潮流转移导致过负荷跳闸。
对级联第一传播阶段的故障线路实施阻断策略后，重新进行仿真得到此时不同N−k场景下的负荷损失，结果如图 5所示。
![]()
图 5 IEEE39节点系统阻断前后对比结果Figure 5. Comparison results of IEEE39 bus system before and after blocking根据表 2得到的高危传播路径辨识结果，在N−1场景下，对线路3进行闭锁后，系统遭受的最大负荷损失由之前的503.7降至172 MW，减小了65.85%；在N−2场景下，对线路3进行闭锁后，系统遭受的最大负荷损失由之前的1 527.1降至1 181.9 MW，减小了22.6%；在N−3场景下，对线路12进行闭锁后，系统遭受的最大负荷损失由之前的2 163.9降至1 891.1 MW，减小了12.61%。因此，对辨识出的级联传播第一阶段故障实施阻断策略后，系统遭受的负荷损失远小于不采取阻断控制策略时。
4.3.2 不同源发故障辨识方法下的故障传播路径对比分析
为进一步验证本文模型相比于经典N−k模型，更适用于高危N−k源发故障场景筛选。将经典N−k模型辨识得到的N−k源发故障场景结果带到本文模型中进行仿真，得到该N−k源发故障场景在考虑级联传播过程后的故障传播路径及负荷损失。
由表 4可知，经典N−k模型在N−1和N−3场景下辨识出的危害最大的源发故障场景并不能引发连锁故障。在N−2场景下经典N−k模型所辨识出的线路35、38虽然能够引发连锁故障，但最终造成的负荷损失只有1 325.6 MW，小于本文模型辨识出的线路1和30所造成的负荷损失1 527.1 MW。
表 4 经典N−k模型故障传播路径辨识结果Table 4. Propagation path identification in N−k modelk 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 32 不能引发连锁故障 172 2 35 38 1 3 6 8 19 23 24 1352.6 3 1 11 12 不能引发连锁故障 863.9 因此，经典N−k模型只通过源发故障阶段来辨识高危N−k源发故障，没有考虑源发故障发生后对其余线路的影响，忽略了故障传播之间的潮流转移相关性，难以辨识出能够引发连锁故障，对系统造成更严重后果的源发故障组合。
4.4 IEEE39节点系统暂态稳定仿真验证
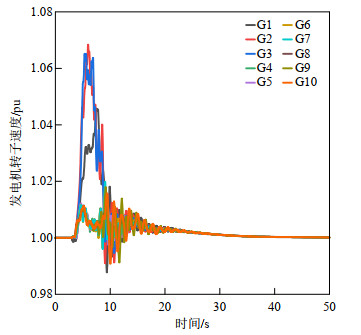
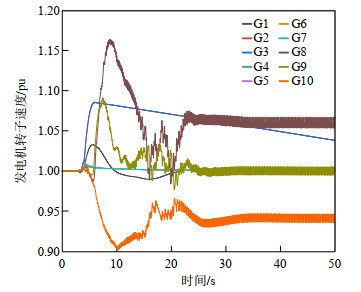
在PowerFactory中搭建IEEE39节点系统的连锁故障时域仿真模型，将本文所辨识出的不同N−k场景下危害最大的源发故障组合线路42，线路1、30，线路1、9、10设置为系统运行3 s后发生故障，进行暂态稳定仿真，结果如图 6—8所示。
由图 6—8可知，不同N−k场景下本文所辨识出的高危源发故障场景发生故障后，发电机都会发生失稳，系统严重振荡。如线路42故障后，在3.57和4.53 s，线路3和线路1相继因潮流转移过载发生故障，系统失稳，直到切除大量负荷后，系统最后才趋于稳定。这与本文所辨识出的高危源发故障与传播路径基本一致。
仿真结果表明，本文模型通过负荷损失大小辨识出的高危源发故障场景在考虑暂态过程后仍能对系统造成较大危害。
4.5 IEEE118节点系统算例分析
4.5.1 IEEE118节点系统对比分析
将本文模型与经典N−k模型[8]进行对比，结果如表 5所示。
由表 5可知，IEEE118节点系统在N−1场景下满足N−1安全准则。因此，在N−1场景下本文模型和经典N−k模型都不会造成负荷损失。在N−2和N−3场景下经典N−k模型所辨识出的N−k源发故障场景负荷损失均远小于本文所提模型。
表 5 IEEE118节点系统不同模型对比结果Table 5. Comparison results of different models in IEEE118 bus systemk 模型 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 本文模型 — — — 0 经典N−k — — — 0 2 本文模型 51 61 66 23 44 45 48 54 146 经典N−k 147 156 — — 42 3 本文模型 51 52 61 66 23 44 45 48 53 54 146 经典N−k 94 147 156 — — 42 以N−2场景为例，增加经典N−k模型中源发故障数量k进行仿真，结果如图 9所示。
![]()
图 9 N−2场景下118节点系统不同模型对比结果Figure 9. Comparison results of different models in IEEE118 bus system in N−2 scenario由图 9可知，在IEEE118节点系统中，本文模型在N−2场景下辨识出的源发故障对系统造成的负荷损失仍比经典N−k模型在N−8场景下对系统造成的负荷损失多46%。
4.5.2 IEEE118节点系统故障传播路径阻断分析
对级联第一传播阶段的故障实施阻断策略后，重新进行仿真得到IEEE118节点系统不同N−k场景下的负荷损失，结果如图 10所示。
![]()
图 10 IEEE118节点系统阻断前后对比结果Figure 10. Comparison results of IEEE118 bus system before and after blocking根据表 5得到高危传播路径辨识结果，在N−2场景下，对线路66进行闭锁后(由图 10可知)，系统遭受的最大负荷损失由146降至42 MW，减小了71.23%；在N−3场景下，对线路66进行闭锁后，系统遭受的最大负荷损失由146降至66 MW，减小了54.79%；因此，在对辨识出的级联传播第一阶段故障实施阻断策略后，也能有效减小IEEE118节点系统的停电规模。
4.6 模型计算效率分析
采用本文所提的两阶段网络流算法和直接采用对偶理论求解本文模型，最优解值及求解时间对比结果如表 6、7所示。
表 6 IEEE 39节点系统最优解值/计算时间表Table 6. IEEE39 bus system optimal solution value and calculation schedule方法 本文方法/s 对偶理论/s k=1 503.7/50 503.7/170 k=2 1 527.1/116 1 527.1/1350 k=3 2 163.9/203 2 163.9/2 455 表 7 IEEE 118节点系统最优解值/计算时间表Table 7. IEEE118 bus system optimal solution value and calculation schedule方法 本文方法/s 对偶理论/s k=1 0/4 438 0/21 560 k=2 146/21 445 ∞(858%)/172 800 k=3 146/105 402 ∞(4555%)/172 800 如表 6、7所示，在IEEE39节点系统中，不同N−k故障场景下，通过本文方法和直接利用对偶理论求解所取得的最优值一样。但在N−2和N−3场景下，前者计算速度相比于后者提升了12倍。
在IEEE118节点系统中，在N−2和N−3场景下采用对偶理论直接对本文模型进行求解时, 计算时间为48 h，gap值仍有858%和4 555%，难以在有限时间内求解成功。
综上所述，本文所提两阶段网络流算法可以在兼顾全局优化效果的前提下大幅提升模型计算速度，实现大规模电力系统的N−k多阶段安全分析。
5. 结论
多元件故障会引发连锁故障，对系统的危害远大于预想值。因此，为提升系统抵御大停电的能力，本文提出了一种计及连锁故障传播路径的电力系统N−k多阶段双层优化及故障场景筛选模型，并通过两阶段网络流算法加快模型求解速度，最后以IEEE39节点和IEEE118节点系统为例进行仿真，结论如下：
1）相比于经典N−k模型无法辨识能够引发连锁故障的高危N−k源发故障场景。本文模型同时考虑了源发故障阶段和级联传播阶段的故障传播特性，辨识出的高危N−k源发故障场景所造成的负荷损失远大于经典N−k模型的结果。
2）本文模型能够辨识出由高危N−k源发故障场景引发的多阶段故障传播路径，对辨识出的级联传播第一阶段线路进行阻断控制后，在不同N−k故障场景下，IEEE39节点系统负荷损失分别减小65.85%、22.6%、12.61%；IEEE118节点系统负荷损失减小71.23%、54.79%，有效减小了停电规模。
3）通过两阶段网络流算法加速求解k阶故障集及传播路径，速度提升至少12倍，实现了大规模电力系统的N−k多阶段安全分析。
本文将连锁故障传播过程融入N−k双层优化模型中，进行高危源发故障场景及故障传播路径辨识。考虑到故障传播过程中可能带来的失稳问题和重合闸闭合后再次跳闸给系统带来的二次冲击，后续将考虑建立融合暂态过程影响的高危N−k源发故障场景及多阶段传播路径辨识的优化模型，并设计相应算法以实现模型在实际电力系统中更好的应用。
-
![]()
图 1 计及连锁故障的电力系统N−k多阶段双层优化及故障场景筛选模型框架
Figure 1. N−k bi-level screening model framework of power system considering cascading failure
![]()
图 4 N−2场景下IEEE39节点系统不同模型对比结果
Figure 4. Comparison results of different models in IEEE39 bus system in N−2 scenario
![]()
图 5 IEEE39节点系统阻断前后对比结果
Figure 5. Comparison results of IEEE39 bus system before and after blocking
![]()
图 9 N−2场景下118节点系统不同模型对比结果
Figure 9. Comparison results of different models in IEEE118 bus system in N−2 scenario
![]()
图 10 IEEE118节点系统阻断前后对比结果
Figure 10. Comparison results of IEEE118 bus system before and after blocking
表 1 基于两阶段网络流算法的高危源发N−k故障及多阶段传播路径辨辨识流程
Table 1 High risk N−k fault identification process based on two-stage Flow network algorithm
步骤 内容 步骤1 设置源发故障数量k和级联传播次数m 步骤2 根据所设置参数求解模型M3，根据式(47)得到最优解z*和级联传播第m阶段线路运行状态为wl, m* 步骤3 根据式(1)和(5)得到模型M3取得最优解z*时的k重源发故障集合S*，并输出。 步骤4 根据式(2)和(9)得到模型M3取得最优解z*时的级联传播第s阶段故障线路集Qs*并输出 步骤5 将wl, m*固定到最优直流潮流模型中，求解最优直流潮流模型式(4)、(19)—(25)，根据式(4)得到此时的负荷损失ΔD*输出 
下载: 导出CSV
表 2 IEEE39节点系统高危N−k源发故障场景及多阶段故障传播路径辨识结果
Table 2 High risk N−k source fault scenario and multi-stage propagation path identification of IEEE39 bus system
k 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 42 3 1 503.7 32 — — 172 19 13 21 22 125.4 2 1 30 3 9 13 24 25 42 1 527.1 35 38 1 3 6 8 19 23 24 1 352.6 26 42 3 1 6 8 9 1 261 3 1 9 10 12 3 6 7 8 13 19 23 24 25 26 30 2 163.9 10 26 42 3 9 1 6 8 11 12 13 15 18 2 124.9 10 19 42 3 12 1 9 13 21 22 23 1 865.5
下载: 导出CSV
表 3 IEEE39节点系统不同模型对比结果
Table 3 Comparison results of different models in IEEE39 bus system
k 模型 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 本文模型 42 3 1 503.7 经典N−k 32 — — 172 2 本文模型 1 30 3 9 13 24 25 42 1 527.1 经典N−k 35 38 — — 356.7 3 本文模型 1 9 10 12 3 6 7 8 13 19 23 24 25 26 30 2 163.9 经典N−k 1 11 12 — — 863.9
下载: 导出CSV
表 4 经典N−k模型故障传播路径辨识结果
Table 4 Propagation path identification in N−k model
k 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 32 不能引发连锁故障 172 2 35 38 1 3 6 8 19 23 24 1352.6 3 1 11 12 不能引发连锁故障 863.9
下载: 导出CSV
表 5 IEEE118节点系统不同模型对比结果
Table 5 Comparison results of different models in IEEE118 bus system
k 模型 源发故障线路 级联传播第一阶段故障线路 级联传播第二阶段故障线路 负荷损失/MW 1 本文模型 — — — 0 经典N−k — — — 0 2 本文模型 51 61 66 23 44 45 48 54 146 经典N−k 147 156 — — 42 3 本文模型 51 52 61 66 23 44 45 48 53 54 146 经典N−k 94 147 156 — — 42
下载: 导出CSV
表 6 IEEE 39节点系统最优解值/计算时间表
Table 6 IEEE39 bus system optimal solution value and calculation schedule
方法 本文方法/s 对偶理论/s k=1 503.7/50 503.7/170 k=2 1 527.1/116 1 527.1/1350 k=3 2 163.9/203 2 163.9/2 455
下载: 导出CSV
表 7 IEEE 118节点系统最优解值/计算时间表
Table 7 IEEE118 bus system optimal solution value and calculation schedule
方法 本文方法/s 对偶理论/s k=1 0/4 438 0/21 560 k=2 146/21 445 ∞(858%)/172 800 k=3 146/105 402 ∞(4555%)/172 800
下载: 导出CSV
-
[1] 李少岩, 曹珂, 顾雪平, 等. 多直流馈入受端系统与直流联络线协调恢复的一体化建模与求解[J]. 电工技术学报, 2023, 38(21): 5862-5877. LI Shaoyan, CAO Ke, GU Xueping, et al. Integrated modeling and solution for coordinated restoration of multi-infeed receiving-end systems and HVDC tie lines [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5862-5877(in Chinese).
[2] 沈政委, 孙华东, 仲悟之, 等. 基于关键事件的高比例新能源电力系统故障连锁演化规律分析[J]. 电力系统自动化, 2022, 46(24): 57-65. DOI: 10.7500/AEPS20220128004 SHEN Zhengwei, SUN Huadong, ZHONG Wuzhi, et al. Key event based analysis of evolution law of cascading failures in power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(24): 57-65(in Chinese). DOI: 10.7500/AEPS20220128004
[3] 汪涛, 武传涛, 随权, 等. 计及故障维修与网络重构的灾后配电网综合调度策略[J]. 中国电机工程学报, 2024, 44(5): 1764-1776. DOI: 10.13334/j.0258-8013.pcsee.221945 WANG Tao, WU Chuantao, SUI Quan, et al. Integrated dispatching strategy for post-disaster distribution networks with fault repair and network reconfiguration [J]. Proceedings of the CSEE, 2024, 44(5): 1764-1776(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.221945
[4] 林伟芳, 易俊, 郭强, 等. 阿根廷"6.16"大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2020, 40(9): 2835-2841. DOI: 10.13334/j.0258-8013.pcsee.191360 LIN Weifang, YI Jun, GUO Qiang, et al. Analysis on blackout in argentine power grid on June 16, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2020, 40(9): 2835-2841(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.191360
[5] 孟荣涛, 李少岩, 顾雪平, 等. 光热电站作为黑启动电源时计及机组恢复效益的运行优化[J]. 电工技术学报, 2023, 38(13): 3486-3498. MENG Rongtao, LI Shaoyan, GU Xueping, et al. Operation optimization considering unit recovery effect when concentrating solar power station acts as black-start power source[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3486-3498(in Chinese).
[6] XIANG Yingmeng, WANG Lingfeng. An improved defender-ttacker-efender model for transmission line defense considering offensive resource uncertainties [J]. IEEE Transactions on Smart Grid, 2019, 10(3): 2534-2546. DOI: 10.1109/TSG.2018.2803783
[7] 柳璐, 李林芝, 卢天琪, 等. 基于网页链接分析的电力系统连锁故障关键环节辨识方法[J]. 电力系统自动化, 2021, 45(10): 25-33. DOI: 10.7500/AEPS20200611004 LIU Lu, LI Linzhi, LU Tianqi, et al. Critical link identification method for cascading failure in power systems based on web link analysis[J]. Automation of Electric Power Systems, 2021, 45(10): 25-33(in Chinese). DOI: 10.7500/AEPS20200611004
[8] ARROYO J M. Bilevel programming applied to power system vulnerability analysis under multiple contingencies [J]. IET Generation, Transmission & Distribution, 2010, 4(2): 178-190.
[9] DU Min, LIU Xuan, ZHOU Quan, et al. Hybrid robust tri-level defense model against multiperiod uncertain attacks[J]. IEEE Transactions on Smart Grid, 2022, 13(4): 3255-3265. DOI: 10.1109/TSG.2021.3139033
[10] 朱元振, 刘玉田. 考虑源荷不确定性的高风险连锁故障快速筛选[J]. 电力系统自动化, 2023, 47(5): 92-103. ZHU Yuanzhen, LIU Yutian. Fast screening of high-risk cascading failure considering uncertainties of source and load[J]. Automation of Electric Power Systems, 2023, 47(5): 92-103(in Chinese).
[11] 刘彤, 李少岩, 顾雪平, 等. 基于图注意力网络算法的电网连锁故障关键线路辨识[J]. 中国电机工程学报, 2022, 42(15): 5448-5458. DOI: 10.13334/j.0258-8013.pcsee.213004 LIU Tong, LI Shaoyan, GU Xueping, et al. Critical line identification of cascading failures in power grid based on graph attention network algorithm[J]. Proceedings of the CSEE, 2022, 42(15): 5448-5458(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.213004
[12] THAMS F, VENZKE A, ERIKSSON R, et al. Efficient database generation for data-driven security assessment of power systems[J]. IEEE Transactions on Power Systems, 2020, 35(1): 30-41. DOI: 10.1109/TPWRS.2018.2890769
[13] 蔡晔, 刘放, 曹一家, 等. 电力信息物理系统低代价多阶段高危攻击策略研究[J]. 电力系统自动化, 2021, 45(20): 1-8. CAI Ye, LIU Fang, CAO Yijia, et al. Research on low-cost multi-stage high-risk attack strategy for power cyber-physical system[J]. Automation of Electric Power Systems, 2021, 45(20): 1-8(in Chinese).
[14] ZHAO Yirui, CAO Yijia, LI Yong, et al. Risk-based contingency screening method considering Cyber-Attacks on substations[J]. IEEE Transactions on Smart Grid, 2022, 13(6): 4973-4976.
[15] 田猛, 董政呈, 龚立, 等. 考虑控制系统-发电机信息物理耦合的脆弱输电线路辨识[J]. 电力系统自动化, 2021, 45(11): 11-18. TIAN Meng, DONG Zhengcheng, GONG Li, et al. Identification of vulnerable transmission line considering cyber-physical coupling of control system and generator[J]. Automation of Electric Power Systems, 2021, 45(11): 11-18(in Chinese).
[16] CHE Liang, LIU Xuan, LI Zuyi. Screening hidden N−k line contingencies in smart grids using a multi-stage model[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1280-1289.
[17] 遆宝中, 李庚银, 王剑晓, 等. 计及监测与控制功能的电力信息物理系统关键输电线路辨识方法[J]. 中国电机工程学报, 2022, 42(7): 2556-2565. DOI: 10.13334/j.0258-8013.pcsee.210483 TI Baozhong, LI Gengyin, WANG Jianxiao, et al. Identification of critical transmission lines in cyber- physical power system considering monitoring function and control function[J]. Proceedings of the CSEE, 2022, 42(7): 2556-2565(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.210483
[18] CHE Liang, LIU Xuan, WEN Yunfeng, et al. Identification of cascading failure initiated by hidden multiple-branch contingency[J]. IEEE Transactions on Reliability, 2019, 68(1): 149-160. DOI: 10.1109/TR.2018.2889478
[19] PENG Datian, DONG Jianmin, YANG Jungang, et al. Dynamical failures driven by false load injection attacks against smart grid[J]. IEEE Transactions on Information Forensics and Security, 2022, 17: 2213-2226. DOI: 10.1109/TIFS.2022.3181860
[20] 李妍莎, 蔡晔, 曹一家, 等. 基于潮流转移相似性的连锁故障高危环节辨识[J]. 中国电机工程学报, 2024, 44(23): 9122-9133. DOI: 10.13334/j.0258-8013.pcsee.230837 LI Yansha, CAI Ye, CAO Yijia, et al. High-risk links identification for cascading failures based on the power flow transfer similarity[J]. Proceedings of the CSEE, 2024, 44(23): 9122-9133(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.230837
[21] CAI Ye, CAO Yijia, LI Yong, et al. Cascading failure analysis considering interaction between power grids and communication networks[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 530-538. DOI: 10.1109/TSG.2015.2478888
[22] 边晓燕, 杨云轶, 黄阮明, 等. 基于机电–电磁混合仿真的交直流混联受端电网连锁故障筛选指标及搜索策略[J]. 中国电机工程学报, 2023, 43(17): 6614-6627. DOI: 10.13334/j.0258-8013.pcsee.221144 BIAN Xiaoyan, YANG Yunyi, HUANG Ruanming, et al. Screening indices and search strategy for AC-DC hybrid receiving-end power grid cascading failures based on hybrid electromechanical-electromagnetic simulation [J]. Proceedings of the CSEE, 2023, 43(17): 6614-6627(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.221144
[23] Figshare. Unified explanation of formulas and variables [EB/OL]. (2024-01-20). https://doi.org/10.6084/m9.figshare.25035104.v1.
[24] KAPLUNOVICH P, TURITSYN K. Fast and reliable screening of N−2 contingencies[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4243-4252. DOI: 10.1109/TPWRS.2015.2510586
[25] 于群, 郝晴晴. 计及重合闸作用的大停电模型与停电风险分析[J]. 电力系统及其自动化学报, 2020, 32(11): 65-72. YU Qun, HAO Qingqing. Blackout model and outage risk analysis considering reclosing[J]. Proceedings of the CSU-EPSA, 2020, 32(11): 65-72(in Chinese).
[26] SGHARI M, FATHOLLAHI-FARD A M, MIRZAPOUR AL-E-HASHEM S M J, et al. Transformation and linearization techniques in optimization: a state-of-the-art survey[J]. Mathematics, 2022, 10(2): 283.
[27] OHNSON E S, DEY S S. A scalable lower bound for the worst-case relay attack problem on the transmission grid [J]. INFORMS Journal on Computing, 2022, 34(4): 2296-2312.
[28] 李少岩, 张友好, 顾雪平. 计及短路故障影响的含风电电力系统恢复决策优化方法[J]. 中国电机工程学报, 2023, 43(20): 7827-7841. DOI: 10.13334/j.0258-8013.pcsee.231177 LI Shaoyan, ZHANG Youhao, GU Xueping. Optimization method of restoration decision-making for wind integrated power system considering the effects of short-circuit fault [J]. Proceedings of the CSEE, 2023, 43(20): 7827-7841(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.231177
[29] 李咸善, 杨拯, 李飞, 等. 基于梯级水电调节的风光水联盟与区域电网联合运行优化调度策略[J]. 中国电机工程学报, 2023, 43(6): 2234-2247. DOI: 10.13334/j.0258-8013.pcsee.212743 LI Xianshan, YANG Zheng, LI Fei, et al. Optimization scheduling strategy for joint operation of wind-solar-water power alliance and regional power grid based on cascade hydropower regulation[J]. Proceedings of the CSEE, 2023, 43(6): 2234-2247(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.212743
[30] MATPOWER USER Manual. (2020-08-03). https://matpower.org/docs/MATPOWERmanual-7.0.pdf.
[31] 张至美, 黄少伟, 梅生伟, 等. 基于合作博弈的电网支路脆弱性评估方法[J]. 电力系统自动化, 2020, 44(6): 9-16. ZHANG Zhimei, HUANG Shaowei, MEI Shengwei, et al. Vulnerability assessment method of branch lines in power grid based on cooperative game [J]. Automation of Electric Power Systems, 2020, 44(6): 9-16(in Chinese).
[32] 周景, 张衡, 刘盾盾, 等. 考虑连锁故障的输电网扩展规划方法[J]. 电力自动化设备, 2021, 41(12): 136-142. ZHOU Jing, ZHANG Heng, LIU Dundun, et al. Expansion planning method of transmission network considering cascading failures[J]. Electric Power Automation Equipment, 2021, 41(12): 136-142(in Chinese).
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
下载:
