永磁轮毂电机最优磁链矢量无权重价值函数模型预测转矩控制

朱孝勇; 乙峰; 张超; 杜怿; 徐磊; 张丽

doi:10.13334/j.0258-8013.pcsee.232234

永磁轮毂电机最优磁链矢量无权重价值函数模型预测转矩控制

江苏大学电气信息工程学院, 江苏省镇江市 212013

基金项目:

国家自然科学基金重点国际(地区)合作研究项目 52320105009

国家自然科学基金项目 52077098

详细信息

作者简介:
朱孝勇(1975)，男，教授，主要从事永磁电机设计、分析与驱动控制等方面的研究工作，zxyff@ujs.edu.cn

乙峰(1998)，男，硕士研究生，主要研究方向为永磁轮毂电机驱动控制技术，2222107075@stmail.ujs.edu.cn

杜怿(1979)，男，博士，教授，主要研究方向为特种电机系统设计、控制与分析，duyie@ujs.edu.cn

徐磊(1988)，男，副教授，主要研究方向为高效永磁电机及其驱动技术、多自由度电机系统、电机电磁场计算等，leixu@ujs.edu.cn

张丽(1987)，女，副教授，主要研究方向为新能源电动汽车电机驱动系统、包括高可靠永磁电机设计、无位置传感器控制、容错控制，jennyzhang@ujs.edu.cn

通讯作者:
张超(1973)，男，教授，研究方向为有源功率解耦变换器及控制技术、小电容永磁电机驱动系统及高性能控制策略技术，superbow@ujs.edu.cn

中图分类号: TM351
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2023-10-15
- 发布日期: 2024-04-21
- 刊出日期: 2025-01-19

Optimal Flux Vector Model Predictive Torque Control Without Weighting Factor for Permanent Magnet Hub Motor

School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, Jiangsu Province, China

Funds:

National Natural Science Foundation of China (International Cooperation Program) 52320105009

National Natural Science Foundation of China 52077098

摘要

摘要: 永磁轮毂电机的外转子通常与轮辋轮胎直接相联结，相比内转子永磁驱动电机，转动惯量较大，其速度响应明显滞后负载变化。因此，复杂运行工况下，永磁轮毂电机驱动系统转速不稳定，电动车辆行走路径易出现偏移。为解决轮毂驱动下电动车辆的这一固有技术难题，提出一种磁链为唯一约束条件的无权重价值函数模型预测转矩控制(model predictive torque control，MPTC)策略，可实现复杂多变动态工况下电动车辆稳定运行的工作需求。所提价值函数将转矩、定子磁链幅值约束统一为定子磁链矢量的优化，消除了权重系数的整定，提高了复杂运行工况下轮毂电机的反应速度。同时，引入有效电压矢量与零电压矢量切换瞬间的定子磁链，以此为评估依据选择最优电压矢量，可降低转矩与定子磁链脉动，从而提高轮毂电机转速控制精度。实验验证了控制方法的正确性和有效性。
- 永磁轮毂电机 /
- 模型预测转矩控制 /
- 最优占空比 /
- 无权重系数 /
- 快速响应
Abstract: The external rotor of permanent magnet hub motor is usually directly connected to the rim tire, which has a larger rotational inertia than the inner rotor permanent magnet drive motor; at the same time, the speed response of the permanent magnet hub motor obviously lags behind the load change. Therefore, under complex operating conditions, the rotational speed of the permanent magnet hub motor drive system is unstable, and the travel path of the electric vehicle is prone to deviation. In order to solve this inherent technical problem of electric vehicles under hub drive, this paper proposes an unweighted cost function model predictive torque control (MPTC) strategy with the magnetic chain as the only constraint, which realizes the stable operation of electric vehicles under complex and variable dynamic working conditions. The cost function proposed in this paper unifies the torque and stator magnetic chain amplitude constraints into the optimization of the stator magnetic chain vector, eliminates the rectification of the weighting factor, and improves the response speed of the hub motor under complex operating conditions. At the same time, the stator magnetic chain at the instant of switching between the effective voltage vector and the zero voltage vector is introduced. This serves as the criterion for selecting the optimal voltage vector, reducing the torque and stator magnetic chain pulsation, and improving the accuracy of hub motor speed control. The experiment verified the correctness and effectiveness of the control method.
- permanent magnet hub motor /
- model predictive torque control /
- optimal duty cycle /
- without weighting factor /
- fast response

HTML全文

0. 引言

永磁轮毂电机具有高效率、高功率/转矩密度、宽调速范围以及结构紧凑等优点。相比集中式驱动，基于轮毂电机的分布式电动车辆无需离合器、传动轴等机械部件，进一步简化了系统结构，提高了传动效率^[1]。同时，分布式驱动通过永磁轮毂电机灵活控制轮胎转向和速度，增加了控制维度和控制灵活性^[2-3]。因此，基于永磁轮毂电机分布式驱动系统在电动汽车、特种电动车辆、电动拖拉机等领域中呈现出独特优势，成为未来发展的重要方向之一。

永磁轮毂电机式驱动系统具有高自由度控制特点的同时，也面临着一系列新的问题与挑战：相对于集中式驱动电动车辆而言，在行驶过程中悬架吸收了大部分的路面冲击力，起到减震的作用。然而，永磁轮毂电机直接面对坑洼、起伏不平以及泥泞等地形地貌，工况复杂程度显著增加^[4-6]。同时，永磁轮毂电机较大的惯性致使电机的速度响应明显滞后外部工况变化，这一问题直接影响分布式车辆的稳定性。例如，救灾用等特种车辆行驶在颠簸震动、泥泞潮湿等极端环境下时，需要在加减速、转向、制动等运行需求中快速转换，永磁轮毂电机上述缺点会导致车辆打滑、侧移等问题。装载机、挖掘机等工程车辆作业时，需面对高低起伏的工程路况、多变的行驶载荷等工况，会产生车辆方向盘难以控制、车辆跑偏等情况。再者，对于电动拖拉机除了要进行平坦道路运输作业，还要完成田间作业如犁耕、除草、开沟、播种等负载作业^[7-8]。由于需要在高低不平、硬度不均匀土壤环境下进行作业，使得拖拉机容易发生侧翻、转向困难等问题。因此，为提高电动车辆的作业质量，永磁轮毂电机必须快速、准确跟踪整车控制器给定转速命令，实现复杂工况和外部扰动下永磁轮毂电机稳定运行以确保电动车辆按指定轨迹行进^[9]。

现有集中式驱动系统普遍采用磁场定向控制、直接转矩控制等策略^[10]，但是难以满足永磁轮毂电机复杂工况下快速、准确速度控制的需求。业内人士与相关学者将自抗扰控制^[11-12]、滑模控制^[13-15]、模型预测控制^[16-19]等方法用于永磁轮毂电机驱动系统。然而自抗扰控制参数众多、调参困难，无法实现复杂多变工况下永磁轮毂电机全局最优控制。滑模控制存在抖振问题，在负载频繁变化时，电动车辆四轮转速易出现不同步的现象。模型预测转矩控制(model predictive torque control，MPTC)通过价值函数针对预测结果优化电压矢量^[20-22]，在以转矩与定子磁链误差最小为约束条件下快速跟踪控制目标，提高永磁轮毂电机的动态性能。但传统MPTC因在一个控制周期内仅能使用一个电压矢量，转矩与定子磁链脉动较大，不利于永磁轮毂电机转速高精度跟踪控制。

为进一步提高MPTC的控制性能，文献[23-25]提出占空比模型预测转矩控制(duty cycle model predictive torque control，DC-MPTC)。该控制策略通过引入零矢量，在每个控制周期内合理配置有效电压矢量和零矢量的作用时间，实现电压矢量幅值连续可调，进一步抑制转矩与定子磁链脉动。但是，该价值函数采用权重系数平衡转矩和定子磁链幅值2个控制目标^[26-27]，不仅权重系数设计验证依赖经验，而且单一权重系数无法应对复杂多变工况。因此，如何优化价值函数成为DC-MPTC亟待解决的难题之一。

文献[28]提出一种权重系数在线排序整定方法，改善了宽速域、大负荷工况下电机的运行性能。但是，该方法在线排序过程较慢，增加了复杂工况下轮毂电机的响应时间。文献[29]提出一种基于矩阵转换器无功补偿的预测控制策略，实现最佳权重系数的自动调整，但同样存动态工况下响应时间变长的缺点。文献[30]设计了基于电压矢量跟踪误差的价值函数，虽然不再需要传统MPTC中定子磁链的权重系数，但是外部扰动工况下价值函数产生的转矩与磁链误差较大，控制效果有待提高。文献[31]的价值函数仅包含电压矢量，避免了权重系数的整定，并利用改进占空比控制对最优矢量进行筛选，提高了电机控制精度，但并未考虑定子磁链控制效果，定子磁链脉动较大。

本文提出一种磁链为唯一约束条件的无权重价值函数模型预测转矩控制策(flux without weighting factor model predictive torque control，FWW-MPTC)。所提无权重价值函数把对转矩、定子磁链幅值的控制等效简化为只对定子磁链矢量的控制，取消了价值函数中的权重系数，提高复杂工况下的轮毂电机动态性能。同时，将有效电压矢量与零电压矢量切换瞬间定子磁链引入价值函数以选择最优电压矢量，进一步降低转矩与定子磁链脉动，提高电机转速精度。最后，通过实验证明了本文所提算法在多工况下永磁轮毂电机转速稳定的有效性。

1. 永磁轮毂电机模型

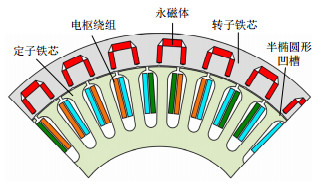
本文以外转子内置式永磁(external rotor interior permanent magnet，ER-IPM)轮毂电机为研究对象，研究复杂工况下轮毂电机驱动车辆高性能控制策略。电机结构如图 1所示，其中定子槽数为36槽，转子极数为50极，轴向长度为45 mm，内置式永磁体沿圆周位于转子内部。该电机在降低永磁体用量的同时，为电动车辆提供大转矩输出。

图 1 ER-IPM轮毂电机结构

Figure 1. Structure of ER-IPM hub motor

下载: 全尺寸图片幻灯片

为简化分析，设ER-IPM轮毂电机的三相绕组对称，无涡流损耗和磁滞损耗。该电机两相旋转d-q坐标系下的电压方程为

$\left\{ {\begin{array}{*{20}{l}} {{u_d} = {R_{\text{s}}}{i_d} - {\omega _{\text{e}}}{\psi _q} + \frac{{\text{d}{\psi _d}}}{{\text{d}t}}} \\ {{u_q} = {R_{\text{s}}}{i_q} + {\omega _{\text{e}}}{\psi _d} + \frac{{\text{d}{\psi _q}}}{{\text{d}t}}} \end{array}} \right.$

(1)

式中：R_s为定子电阻；ω_e为转子电角速度；u_d，u_q分别为d，q轴定子电压；i_d，i_q分别为d，q轴定子电流；ψ_d，ψ_q分别为d，q轴定子磁链。磁链方程满足：

$\left\{ {\begin{array}{*{20}{l}} {{\psi _d} = {L_d}{i_d} + {\psi _{\text{f}}}} \\ {{\psi _q} = {L_q}{i_q}} \end{array}} \right.$

(2)

式中：L_d，L_q分别为d，q轴定子电感；ψ_f为永磁体磁链。

电磁转矩方程为

${T_{\text{e}}} = \frac{3}{2}p{i_q}[{i_d}({L_d} - {L_q}) + {\psi _{\text{f}}}]$

(3)

式中：T_e为电磁转矩；P为极对数。

机械运动方程为

$J{\dot \omega _{\text{m}}} = {T_{\text{e}}} - {T_\text{L}} - B{\omega _{\text{m}}}$

(4)

式中：T_L为负载转矩；J为转子等效转动惯量；B为粘滞摩擦系数；ω_m为转子机械角速度，它与ω_e满足关系ω_e=Pω_m。

2. DC-MPTC策略工作原理

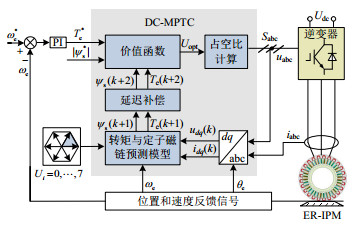
DC-MPTC策略将预测转矩与定子磁链作为控制目标引入到价值函数，意图提高复杂工况下轮毂电机系统转矩与定子磁链的控制精度。该控制原理框图如图 2所示。首先利用位置和速度反馈信号推出转矩与定子磁链预测模型，其次通过该预测模型及其延迟补偿模块构造价值函数；然后计算6个扇区内对应的有效电压矢量，同时通过价值函数最小化来选择最优电压矢量并计算其在一个控制周期内的占空比，在这基础上其余部分时间施加零电压矢量；最后作用于逆变器控制轮毂电机运行。图 2表明：构建合理的价值函数是实现DC-MPTC控制策略高性能运行的关键环节。

图 2 DC-MPTC原理框图

Figure 2. Control block diagram of DC-MPTC

下载: 全尺寸图片幻灯片

2.1 预测模型

把式(2)代入式(1)，建立以定子电流为状态变量的永磁同步电机数学模型：

$\left\{ {\begin{array}{*{20}{l}} {\frac{{\text{d}{i_d}}}{{\text{d}t}} = \frac{1}{{{L_d}}}{u_d} + \frac{{{L_q}{\omega _{\text{e}}}}}{{{L_d}}}{i_q} - \frac{{{R_{\text{s}}}}}{{{L_d}}}{i_d}} \\ {\frac{{\text{d}{i_q}}}{{\text{d}t}} = \frac{1}{{{L_q}}}{u_q} - \frac{{{R_{\text{s}}}}}{{{L_q}}}{i_q} - \frac{{{L_d}{\omega _{\text{e}}}}}{{{L_q}}}{i_d} - \frac{{{\psi _{\text{f}}}{\omega _{\text{e}}}}}{{{L_q}}}} \end{array}} \right.$

(5)

以T_s作为系统的采样周期，对式(5)展开前向欧拉公式离散，可得k+1时刻d、q轴定子电流的预测方程：

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {i_d}(k + 1) = {i_d}(k) + [\frac{1}{{{L_d}}}{u_d}(k) + \frac{{{L_q}{\omega _{\text{e}}}}}{{{L_d}}}{i_q}(k) - \frac{{{R_{\text{s}}}}}{{{L_d}}} \cdot \hfill \\ \quad \quad \quad \quad {i_d}(k)]{T_{\text{s}}} \hfill \\ \end{array} \\ \begin{array}{l} {i_q}(k + 1) = {i_q}(k) + [\frac{1}{{{L_q}}}{u_q}(k) - \frac{{{L_d}{\omega _{\text{e}}}}}{{{L_q}}}{i_d}(k) - \hfill \\ \quad \frac{{{R_{\text{s}}}}}{{{L_q}}}{i_q}(k) - \frac{{{\psi _{\text{f}}}{\omega _{\text{e}}}}}{{{L_q}}}]{T_{\text{s}}} \hfill \\ \end{array} \end{array}} \right.$

(6)

对式(1)离散化可得k+1时刻d、q轴定子磁链预测表达式，即：

$\left\{ \begin{gathered} {\psi _d}(k + 1) = {\psi _d}(k) + [{u_d}(k) - {R_{\text{s}}}{i_d}(k) + {\omega _{\text{e}}}(k){\psi _q}(k)]{T_{\text{s}}} \hfill \\ {\psi _q}(k + 1) = {\psi _q}(k) + [{u_d}(k) - {R_{\text{s}}}{i_q}(k) - {\omega _{\text{e}}}(k){\psi _d}(k)]{T_{\text{s}}} \hfill \\ \end{gathered} \right.$

(7)

然而，实际运行时因控制系统存在采样、通讯等延迟环节，降低了动态工况下轮毂电机响应速度。为此，需对控制延迟进行补偿来提高控制性能。

由式(7)可以得到k+2时刻d、q轴定子磁链的预测表达式为

$\left\{ {\begin{array}{*{20}{l}} {\psi _d}(k + 2) = {\psi _d}(k + 1) + [{u_d}(k + 1) - \hfill \\ \quad \quad \quad \quad {R_{\text{s}}}{i_d}(k + 1) + {\omega _{\text{e}}}{\psi _q}(k + 1)]{T_{\text{s}}} \hfill \\ {\psi _q}(k + 2) = {\psi _q}(k + 1) + [{u_d}(k + 1) - \hfill \\ \quad \quad \quad \quad {R_{\text{s}}}{i_q}(k + 1) - {\omega _{\text{e}}}{\psi _d}(k + 1)]{T_{\text{s}}} \hfill \\ \end{array}} \right.$

(8)

结合式(3)、(6)、(8)，k+2时刻轮毂电机的转矩、定子磁链预测方程为：

${T_{\text{e}}}(k + 2) = \frac{3}{2}p{i_q}(k + 2)[{i_d}(k + 2)({L_d} - {L_q}) + {\psi _{\text{f}}}]$

(9)

$\left| {{\psi _{\text{s}}}(k + 2)} \right| = \sqrt {{{[{\psi _d}(k + 2)]}^2} + {{[{\psi _q}(k + 2)]}^2}}$

(10)

由式(9)、式(10)可得电机转矩与定子磁链的预测值，进一步结合转矩与定子磁链给定值获取两者对应的误差值，以二者误差值为约束条件可构造相应的价值函数。

2.2 价值函数特性分析

考虑延迟补偿因素，DC-MPTC策略将转矩和磁链的预测值与给定值构建价值函数，即：

${g_1} = \left| {T_{\text{e}}^* - {T_{\text{e}}}(k + 2)} \right| + A\left| {\left| {\psi _{\text{s}}^*} \right| - \left| {{\psi _{\text{s}}}(k + 2)} \right|} \right|$

(11)

式中：A为定子磁链项的权重系数；T_e^*与|ψ_s^*|分别为转矩与定子磁链幅值的给定值。该价值函数通过选择转矩与定子磁链脉动最小的电压矢量以抑制电机转矩脉动。

DC-MPTC在获得有效电压矢量U_i后，结合零电压矢量U₀共同作用于逆变器。U₀、U_i这2个矢量作用于轮毂电机对应转矩变化率s₀和s_i分别为：

${s_0} = \frac{3}{2}p{\psi _{\text{f}}}[(1 - \frac{{{R_{\text{s}}}{T_{\text{s}}}}}{{{L_q}}}){i_q}(k) - \frac{{{L_d}{T_{\boldsymbol{s}}}{\omega _{\text{e}}}}}{{{L_q}}}{i_d}(k) - \frac{{{\psi _{\text{f}}}{T_{\text{s}}}{\omega _{\text{e}}}}}{{{L_q}}}]$

(12)

${s_{\text{i}}} = {s_0} + \frac{{3p{\psi _{\text{f}}}{T_{\text{s}}}{\omega _{\text{e}}}}}{{2{L_q}}}$

(13)

由转矩无差拍原理可知T_e^*=T_e(k+1)，同时结合式(12)、(13)可得：

$T_{\text{e}}^* = {T_{\text{e}}}(k + 1) = {T_{\text{e}}}(k) + [{s_{\text{i}}}d + {s_0}(1 - d)]{T_{\text{s}}}$

(14)

改写式(14)可得DC-MPTC在一个周期内有效电压矢量的占空比d为

$d = \frac{{T_{\text{e}}^* - {T_{\text{e}}}(k) - {s_0}{T_{\text{s}}}}}{{({s_{\text{i}}} - {s_0}){T_{\text{s}}}}}$

(15)

式(15)表明：DC-MPTC策略在获取最优电压矢量后，通过计算实现转矩预测误差最小的d并作用于逆变器实现电机转矩脉动抑制。

然而，式(11)所示价值函数存在2个突出问题：1）转矩与定子磁链的量纲和幅值范围存在较大的差异；2）动态工况下轮毂电机转矩和定子磁链对控制变量的响应速度不同。上述2个问题不仅导致权重系数设计困难，而且单一权重系数也无法满足复杂多变工况下电动车辆广域高性能运行。

3. FWW-MPTC控制器设计

为解决上述问题，本文提出一种无权重系数的模型预测转矩控制策略。该控制策略的价值函数把传统价值函数中转矩、定子磁链幅值的控制统一转化为定子磁链矢量的控制，避免了传统价值函数中权重系数的设计与整定。因价值函数移除转矩约束条件，只通过定子磁链来控制系统的转矩输出，所以控制系统具有更快的转矩响应，提高了复杂动态工况下的轮毂电机响应速度。此外，该控制策略将有效电压矢量与零电压矢量切换瞬间的定子磁链引入价值函数，获取电压矢量的全局最优解，达到动态工况下转矩与定子磁链之间的最优平衡，进一步提高电机的控制精度。

3.1 定子磁链矢量特性分析

本文利用i_d=0控制作为调制策略，因此将定子磁链幅值|ψ_s^*|和负载角θ_sf作为控制变量，转矩可以表示为

${T_{\text{e}}} = \frac{3}{2}p\frac{1}{{{L_q}}}{\psi _{\text{f}}}\left| {{\psi _{\text{s}}}} \right|\sin {\theta _{\text{sf}}}$

(16)

式中：θ_sf为负载角，即定子磁链参考值与永磁磁链之间的夹角。式(16)表明，电机转矩可由定子磁链幅值和负载角得到。

轮毂电机定子磁链幅值和转矩参考值可分别表示为：

$\left| {\psi _{\text{s}}^*} \right| = \sqrt {\psi {{_{\text{f}}^{}}^2} + {{({L_q}{i_q})}^2}}$

(17)

$T_{\text{e}}^* = \frac{3}{2}p{\psi _{\text{f}}}{i_q}$

(18)

把式(18)代入式(17)可得：

$\left| {\psi _{\text{s}}^*} \right| = \sqrt {\psi {{_{\text{f}}^{}}^2} + {{(\frac{{2T_{\text{e}}^*{L_q}}}{{3P{\psi _{\text{f}}}}})}^2}}$

(19)

式(19)表明，根据轮毂电机转矩给定值和电机转子磁链可得的电机定子磁链幅值。由式(16)可知，当给定转矩参考值T_e^*和定子磁链参考值|ψ_s^*|时，负载角参考值为

${\theta _{\text{sf}}} = \arcsin (\frac{{2T_{\text{e}}^*{L_q}}}{{3p{\psi _{\text{f}}}\left| {\psi _{\text{s}}^*} \right|}})$

(20)

式(20)表明：由电机给定转矩及定子磁链幅值可以得出负载角参考值。此时，定子磁链参考矢量角为

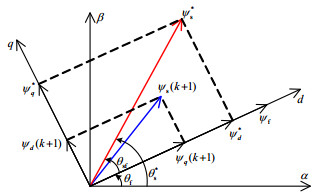
$\theta _{\text{s}}^* = {\theta _{\text{f}}} + {\theta _{\text{sf}}}$

(21)

该式表明定子磁链参考矢量角θ_s^*可由θ_sf与θ_f得到，如图 3所示。

图 3 定子磁链空间矢量图

Figure 3. Space vector diagram of stator flux

下载: 全尺寸图片幻灯片

结合式(19)与式(21)，定子磁链参考矢量表示为

$\boldsymbol{\psi} _{\text{s}}^* = \left| {\psi _{\text{s}}^*} \right|{\text{e}^{\text{j}\theta _{\text{s}}^*}} = \sqrt {\psi {{_{\text{f}}^{}}^2} + {{(\frac{{2T_{\text{e}}^*{L_q}}}{{3P{\psi _{\text{f}}}}})}^2}} {\text{e}^{\text{j}({\theta _{\text{f}}} + {\theta _{\text{sf}}})}}$

(22)

式(22)展示了理想定子磁链与转矩和负载角之间的关系，它表明价值函数(11)中的转矩、定子磁链幅值约束条件可以转换为以定子磁链矢量为约束条件。对比式(11)中的约束项可知，新的约束条件可以避免传统价值函数利用权重系数平衡约束项中不同变量量纲的缺点。

3.2 无权重系数价值函数设计

由式(22)可进一步构造无权重价值函数以选择有效电压矢量。为使转矩与定子磁链预测值准确跟踪定子磁链参考矢量，在上述约束条件下本文将ψ_s^*进行解耦，以d、q轴定子磁链分量为约束条件构造价值函数。ψ_s^*在d、q轴上解耦的分量为

$\left\{ {\begin{array}{*{20}{l}} {\psi _d^* = \left| {\psi _{\text{s}}^*} \right|\cos {\theta _{\text{sf}}}} \\ {\psi _q^* = \left| {\psi _{\text{s}}^*} \right|\sin {\theta _{\text{sf}}}} \end{array}} \right.$

(23)

结合式(8)k+2时刻d，q轴预测定子磁链，进一步构造无权重价值函数为

${g_2} = \left| {\psi _d^* - {\psi _d}(k + 2)} \right| + \left| {\psi _q^* - {\psi _q}(k + 2)} \right|$

(24)

式(24)表明：该价值函数仅以定子磁链误差为约束项，避免了传统价值函数中权重系数整定的问题。

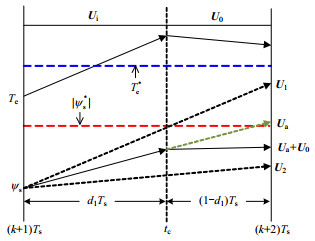
式(24)所述价值函数以k+2时刻的定子磁链误差为约束条件选择有效电压矢量U_a。由式(15)得U_a的占空比为d₁，其与U_a对应转矩、定子磁链误差关系如图 4所示。图 4表明：与其他电压矢量相比，k+2时刻U_a的定子磁链与|ψ_s^*|误差最小。然而U_a在一个控制周期内只作用时长d₁T_s，在2个电压矢量切换瞬间t_c时刻的定子磁链与转矩具有较大误差。同时，在(1−d₁)T_s区间U₀会使转矩减小，而定子磁链幅值基本不变^{[18, 29]}，所以在U_a与U₀组合电压矢量作用后，t_c时刻的定子磁链误差会持续到k+2时刻，控制周期结束时定子磁链仍具有较大误差。由式(16)定子磁链与转矩的关系进一步可知，上述磁链误差会导致转矩存在较大误差。因此，由式(23)获取的电压矢量U_a不能达到最佳控制要求。

图 4 电压矢量U_a与转矩、定子磁链波动曲线

Figure 4. Voltage vector U_a and fluctuation curve of torque and stator flux linkage

下载: 全尺寸图片幻灯片

为解决该问题，本文在式(24)价值函数的基础上，将有效电压矢量U_i与零电压矢量U₀切换瞬间的定子磁链ψ_{s_c}引入无权重价值函数式(24)中，并以ψ_{s_c}误差最小为约束条件来选择电压矢量。

已知有效电压矢量的占空比d，结合式(7)可得U_i与U₀切换瞬间的d、q轴预测定子磁链

$\left\{ {\begin{array}{*{20}{l}} \begin{gathered} {\psi _{d\_{\text{c}}}} = {\psi _d}(k + 1) + d{T_{\text{s}}}{U_{\text{i}d}}(k + 1) - \hfill \\ {\text{ }}[{R_{\text{s}}}{i_d}(k + 1) - {\omega _{\text{e}}}{\psi _q}(k + 1)]{T_{\text{s}}} \hfill \\ \end{gathered} \\ \begin{gathered} {\psi _{q\_{\text{c}}}} = {\psi _q}(k + 1) + d{T_{\text{s}}}{U_{{\text{i}}q}}(k + 1) - \hfill \\ {\text{ }}[{R_{\text{s}}}{i_q}(k + 1) + {\omega _{\text{e}}}{\psi _d}(k + 1)]{T_{\text{s}}} \hfill \\ \end{gathered} \end{array}} \right.$

(25)

式中：U_id(k+1)、U_iq(k+1)分别是有效电压矢量U_i在k+1时刻的d、q轴分量；ψ_{d_c}与ψ_{q_c}分别为切换瞬间定子磁链ψ_{s_c}的d、q轴分量。引入2个电压矢量切换瞬间定子磁链后，无权重价值函数最终设计为

${g_\text{F}} = \left| {\psi _d^* - {\psi _{d\_{\text{c}}}}} \right| + \left| {\psi _q^* - {\psi _{q\_{\text{c}}}}} \right|$

(26)

式(26)表明：该价值函数以降低切换瞬间定子磁链ψ_{s_c}与定子磁链参考值|ψ_s^*|之间的误差为约束条件，并据此选择最优电压矢量 ${{\boldsymbol{U'}}_{\text{a}}}$ 。

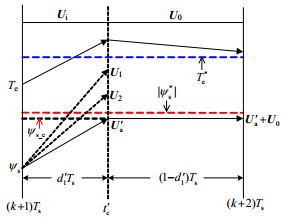
由式(15)得 ${{\boldsymbol{U'}}_{\text{a}}}$ 的占空比为 ${d'_1}$ ，其与 ${{\boldsymbol{U'}}_{\text{a}}}$ 对应转矩、定子磁链误差关系如所示。表明：与其他电压矢量相比， ${t'_{\text{c}}}$ 时刻电压矢量 ${{\boldsymbol{U'}}_{\text{a}}}$ 的定子磁链与|ψ_s^*|之间的误差最小，从而使得 ${t'_{\text{c}}}$ 时刻的转矩误差最小。同时由上文可知，U₀作用后k+2时刻的定子磁链误差也到达最小。因此，k+2时刻实际转矩可以趋近于T_e^*，转矩误差近似为0，进一步降低转矩脉动，实现轮毂电机转速控制精度的提高。

图 5 电压矢量U′_a与转矩、定子磁链波动曲线

Figure 5. Voltage vector U′_a and fluctuation curve of torque and stator flux linkage

下载: 全尺寸图片幻灯片

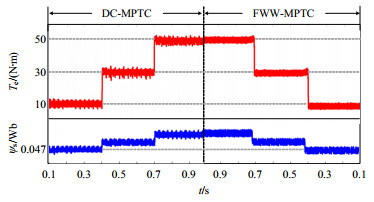
为了验证所提新型价值函数g_F相比于无权重价值函数g₂具有更优良的控制精度，本文给定仿真工况：转速为100 r/min，负载转矩分别为10、30和50 N·m。其仿真波形如图 6所示，对比结果见表 1。可见，相比于基于g₂价值函数的DC-MPTC，基于g_F价值函数FWW-MPTC的转矩与定子磁链脉动均有所降低，转矩脉动分别降低了13.6%、16.8%和13.3%，同时，定子磁链脉动分别降低了15.8%、14.3%和12.5%。

图 6 基于不同价值函数控制策略的仿真波形

Figure 6. Simulation waveform based on different cost function control strategies

下载: 全尺寸图片幻灯片

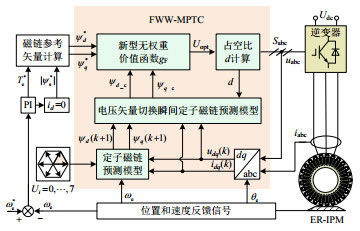
表 1 基于不同价值函数控制策略的仿真对比结果

Table 1. Simulation results based on different cost function control strategies

控制策略	基于g₂价值函数DC-MPTC	基于g_F价值函数FWW-MPTC	降低百分比/%
转矩脉动/(N·m)	3.75	3.24	13.6
	4.53	3.77	16.8
	4.87	4.22	13.3
磁链脉动/Wb	0.019	0.016	15.8
	0.021	0.018	14.3
	0.024	0.021	12.5

下载: 导出CSV

| 显示表格

上述分析可知，FWW-MPTC通过将转矩和定子磁链幅值的控制转换为对定子磁链矢量的控制，避免权重系数的设计与整定问题。同时，新型价值函数引入有效电压矢量与零电压矢量切换瞬间的定子磁链，以此选择出全局最优电压矢量。该电压矢量结合其占空比输出来降低转矩与定子磁链预测误差，实现动态工况下转矩与定子磁链最优平衡，进一步提升轮毂电机的动态响应速度和转速精度。FWW-MPTC整体原理框图，如图 7所示。

图 7 FWW-MPTC原理框图

Figure 7. Control block diagram of FWW-MPTC

下载: 全尺寸图片幻灯片

4. 实验研究

本文以Rtunit半实物仿真系统为核心，搭建了如图 8所示的ER-IPM轮毂电机驱动控制系统实验平台。该平台主要包括RTU-BOX204控制器、Rtunit驱动器、ER-IPM轮毂电机、滚筒、加压装置、磁粉制动器以及扭矩传感器等。滚筒用于模拟车辆行驶路面；加压装置通过施加压力来模拟车辆的作业重量；扭矩传感器用于测量ER-IPM轮毂电机的转速、转矩等参数，其量程为200 N·m，精度为0.2%。系统采样频率和逆变器开关频率均设置为10 kHz(T_s=100 μs)，PWM死区设置为1 μs，直流母线电压给定72 V。本文所采用的ER-IPM轮毂电机模型的相关参数见表 2所示。

图 8 ER-IPM轮毂电机驱动系统实验平台

Figure 8. Drive system experimental platform for ER-IPM hub motor

下载: 全尺寸图片幻灯片

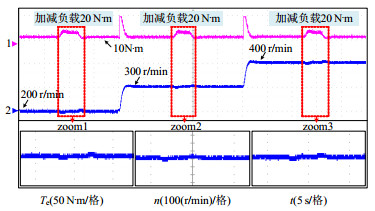
表 2 ER-IPM轮毂电机参数

Table 2. Parameters of ER-IPM hub motor

参数	数值	参数	数值
额定转速/(r/min)	300	额定电压/V	72
额定转矩/(N·m)	40	永磁体磁链/Wb	0.047
额定功率/kW	6	极对数	25
额定电流/A	72	定子电阻/Ω	0.14
d轴电感/mH	1.272	q轴电感/mH	1.62
转动惯量/(kg·m²)	1.398	轮毂直径/cm	62

下载: 导出CSV

| 显示表格

本文所提控制算法主要目标是实现电动车辆在复杂工况作业时的稳定运行。由于轮毂电机惯性较大，电动汽车在高速运行时，外部工况对转速稳定性影响较弱。如图 9所示，轮毂电机转速为200~400 r/min，在外部负载20 N·m扰动下，电机转速基本不受影响。因此，实验中主要模拟电动拖拉机道路运输、快速转场以及田间犁耕等复杂工况，开展变速变载实验来验证轮毂电机的稳定性。基于上述分析，本文实验中轮毂电机转速范围设为30~ 100 r/min，对应电动拖拉机车速为4~12 km/h，转矩范围设为5~30 N·m。为了验证本文所提的FWW-MPTC策略的优越性与有效性，论文对比不同权重系数下的DC-MPTC策略及FWW-MPTC策略的控制效果，以验证复杂工况下本文所提出的FWW-MPTC策略抑制外部负载扰动的有效性。

图 9 转速为200~400 r/min在20 N·m负载下扰动实验波形

Figure 9. Speed of 200~400 r/min under 20 N·m load disturbance experiment waveform

下载: 全尺寸图片幻灯片

实验中为了简化式(11)价值函数的权重系数调节复杂度，利用标幺化值函数，即

${g_3} = \frac{{\left| {T_{\text{e}}^* - {T_{\text{e}}}(k + 2)} \right|}}{{\left| {{T_{\text{en}}}} \right|}} + A\frac{{\left| {\left| {\psi _{\text{s}}^*} \right| - \left| {{\psi _{\text{s}}}(k + 2)} \right|} \right|}}{{\left| {{\psi _{\text{sn}}}} \right|}}$

(27)

式中：T_en为电磁转矩额定值；ψ_sn为磁链幅值额定值。为了充分分析所提控制策略与不同权重系数下的DC-MPTC策略的差异，下述实验以式(27)为价值函数，将A分别取值为0.2、0.8、2来进行实验。

4.1 稳态性能分析

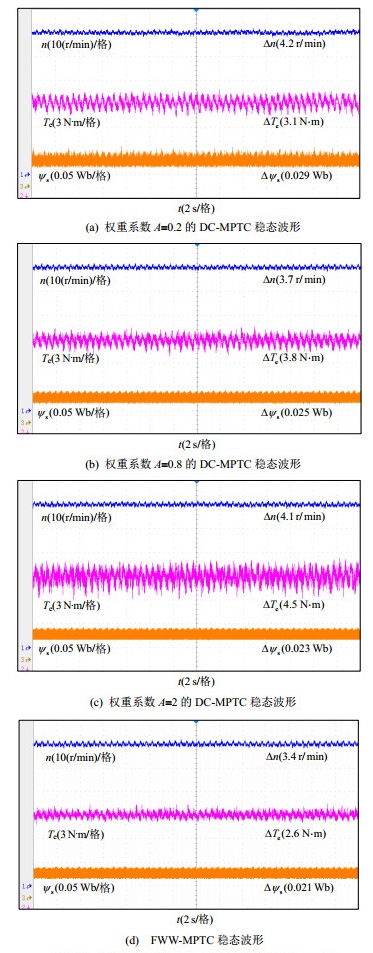
为了验证本文所提方法在稳态下的控制效果，首先模拟电动拖拉机在平坦道路上运输作业工况：转速为60 r/min、转矩为20 N·m。图 10为不同权重系数下DC-MPTC和FWW-MPTC策略下稳态实验波形，图 10中从上到下依次为转速、转矩和定子磁链实验波形。

图 10 转速为60 r/min和负载为20 N·m下不同控制策略的稳态实验波形

Figure 10. Steady-state experimental waveforms of different control strategies under speed of 60 r/min and load of 20 N·m

下载: 全尺寸图片幻灯片

由图 10(a)—(c)实验波形表明：由于DC-MPTC需要权重系数来衡量转矩与定子磁链的比重，当权重系数A值从低到高时，转速脉动依次为4.2、3.7、4.1 r/min，转矩脉动依次为3.1、3.8、4.5 N·m，定子磁链脉动依次为0.029、0.025、0.023 Wb。由此可以看出权重系数越来越大时，DC-MPTC策略下转矩脉动越来越大，定子磁链脉动越来越小，同时转速在权重系数A为0.8时最稳定。

由图 10(d)实验数据表明：本文所提出的FWW-MPTC的转速脉动为3.4 r/min，与DC-MPTC相比，分别降低了19%、8.1%和17.1%；FWW-MPTC的转矩脉动为2.6 N·m，与DC-MPTC相比，分别降低了16.1%、31.6%和42.2%；FWW-MPTC的定子磁链脉动为0.021 Wb，与DC-MPTC相比，分别降低了27.6%、16%和8.7%。相同运行工况下，由于FWW-MPTC的价值函数加入了瞬时定子磁链来选择最优电压矢量，实现轮毂电机在低转矩、定子磁链脉动下稳定运行。

实验结果表明：相同工况下，DC-MPTC的不同权重系数会影响到轮毂电机的转矩、转速。与DC-MPTC相比，本文所提方法的转矩与定子磁链脉动明显减小，转速更为稳定。

4.2 变速实验性能分析

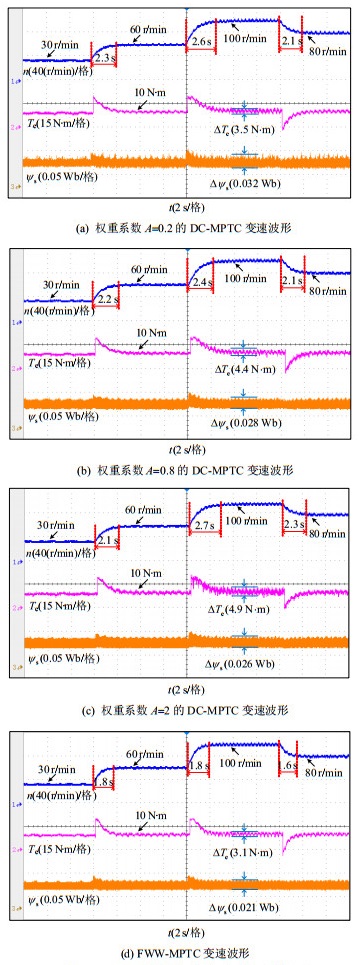
为了验证本文所提方法在变速下的动态响应性能，模拟电动拖拉机快速转场作业工况：负载转矩设定为10 N·m，初始转速为30 r/min，突增转速为60 r/min，继续突增转速为100 r/min，最后将转速降为80 r/min。图 11为不同权重系数下DC-MPTC和FWW-MPTC策略下变速实验波形，图中从上到下依次为转速、转矩和定子磁链实验波形。

图 11 不同控制策略的变速实验波形

Figure 11. Experimental waveforms of variable speed with different control strategies

下载: 全尺寸图片幻灯片

由图 11(a)—(d)变速实验数据表明：当轮毂电机从30 r/min到60 r/min升速时，3种不同权重系数下DC-MPTC策略的响应时间分别为2.3 s、2.2 s、2.1 s。而本文所提出的FWW-MPTC所需响应时间1.8 s，与DC-MPTC相比，响应时间分别缩短了21.7%、18.2%和14.3%。

当电机从60 r/min到100 r/min升速时，3种不同权重系数下DC-MPTC策略的响应时间分别为2.6、2.4、2.7 s。而FWW-MPTC所需响应时间为1.8 s，与DC-MPTC相比，响应时间分别缩短了30.8%、25%和33.3%；

当电机从100 r/min到80 r/min降速时，3种不同权重系数下DC-MPTC策略的响应时间分别为2.1、2.1、2.3 s。而FWW-MPTC所需响应时间为1.6 s，与DC-MPTC相比，响应时间分别缩短了23.8%、23.8%和30.4%。

进一步，由转矩和定子磁链波形可知，DC-MPTC的价值函数因受不同权重系数的影响，其选择的电压矢量并非最优矢量，因此导致在不同转速下，转矩与定子磁链脉动较大。而FWW-MPTC引入瞬时定子磁链预测用于最优电压矢量的选择，在变转速工况下能够利用新型价值函数选择最优电压矢量并作用于轮毂电机。从图 11(d)可以看出，本文所提控制策略在变速过程中的转矩脉动为3.1 N·m，与DC-MPTC相比，分别降低了11.4%、29.5%和36.7%；定子磁链脉动为0.021 Wb，与DC-MPTC相比，分别降低了34.4%、25%和19.2%。因此在相同的动态工况下，FWW-MPTC能够使轮毂电机在低转矩脉动和低定子磁链脉动下稳定运行。

变速实验结果表明：在模拟电动拖拉机快速转场工况下，基于FWW-MPTC策略能够使轮毂电机转速快速跟踪给定指令，有效改善了变速工况下轮毂电机的响应性能，同时提高了系统的稳定性。

4.3 变载实验性能分析

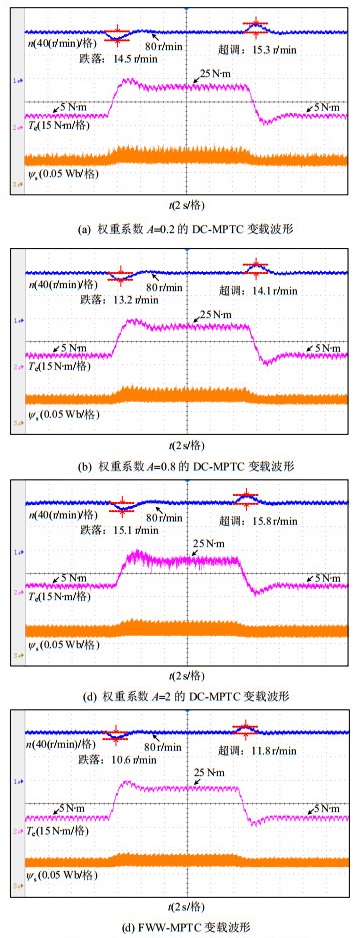
为了验证本文所提方法在负载急剧突变下的动态性能，模拟电动拖拉机在田间的恶劣作业工况：轮毂电机以80 r/min的转速运行，负载从5 N·m突增为25 N·m，然后再突降为5 N·m。图 12为不同权重系数下DC-MPTC和FWW-MPTC策略下变载实验波形，图 12从上到下依次为转速、转矩和定子磁链实验波形。

图 12 不同控制策略的变载实验波形

Figure 12. Experimental waveforms of variable load with different control strategies

下载: 全尺寸图片幻灯片

由图 12(a)—(d)变载实验数据表明：当负载从5 N·m突增为25 N·m时，3种不同权重系数下DC-MPTC策略的轮毂电机转速最大跌落值分别为14.5、13.2、15.1 r/min。而FWW-MPTC转速最大跌落值为10.6 r/min，与DC-MPTC相比，所跌落的转速最大值分别降低了26.9%、19.7%和29.8%。

当负载从25 N·m突降为5 N·m时，3种不同权重系数下DC-MPTC策略的轮毂电机转速最大超调量分别为15.3、14.1、15.8 r/min。而FWW-MPTC转速最大超调量为11.8 r/min，与DC-MPTC相比，所超调的转速最大值分别降低了22.9%、16.3%和25.3%。

经过图 12对比可以发现，FWW-MPTC的动态调整时间有所相同，但转速波动更小，电机的动态性能得到提高。此外，FWW-MPTC的价值函数因具备预测切换时刻的定子磁链的特点，能选择最优电压矢量，有效降低了在外部负载扰动工况下轮毂电机的转矩与定子磁链脉动。

变载实验结果表明：在模拟电动拖拉机在田间作业中，DC-MPTC需调节权重系数来适应外部负载扰动工况下的有效运行，而FWW-MPTC策略避免了权重系数的整定。同时，基于FWW-MPTC策略的轮毂电机驱动系统转矩能够对外部负载扰动及时响应，有效降低了外部扰动对系统的影响，提高了电动拖拉机在田间坑洼路面的抗干扰性能。

5. 结论

本文针对轮毂电机驱动电动车辆在作业时的复杂工况，以ER-IPM轮毂电机为研究对象，提出一种仅以磁链为约束条件的无权重价值函数的模型预测转矩控制策略。分析得到以下结论：

1）与DC-MPTC相比，该策略消除了权重系数难以设计及整定的问题，同时能够有效降低转矩与定子磁链脉动，提高电机转速控制精度。

2）通过模拟实验平台对不同权重系数下DC-MPTC和FWW-MPTC这2种策略在稳态、变速和变载实验条件下进行对比分析，结果表明所提出的FWW-MPTC能够均衡转矩和定子磁链控制，具有更好的转速稳定性能。

3）在转速或转矩突变时，FWW-MPTC能够快速、准确跟踪给定转速的同时，显著提高轮毂电机的抗扰动性能，从而能够实现特种车辆、农用电动拖拉机等电动车辆在复杂环境下高精度作业。

然而，该策略依赖于电机参数，且动态工况下参数易失配会加剧恶化控制性能，对此后续工作将围绕提升电机参数鲁棒性工作展开。

图 1 ER-IPM轮毂电机结构

Figure 1. Structure of ER-IPM hub motor

下载: 全尺寸图片幻灯片

图 2 DC-MPTC原理框图

Figure 2. Control block diagram of DC-MPTC

下载: 全尺寸图片幻灯片

图 3 定子磁链空间矢量图

Figure 3. Space vector diagram of stator flux

下载: 全尺寸图片幻灯片

图 4 电压矢量U_a与转矩、定子磁链波动曲线

Figure 4. Voltage vector U_a and fluctuation curve of torque and stator flux linkage

下载: 全尺寸图片幻灯片

图 5 电压矢量U′_a与转矩、定子磁链波动曲线

Figure 5. Voltage vector U′_a and fluctuation curve of torque and stator flux linkage

下载: 全尺寸图片幻灯片

图 6 基于不同价值函数控制策略的仿真波形

Figure 6. Simulation waveform based on different cost function control strategies

下载: 全尺寸图片幻灯片

图 7 FWW-MPTC原理框图

Figure 7. Control block diagram of FWW-MPTC

下载: 全尺寸图片幻灯片

图 8 ER-IPM轮毂电机驱动系统实验平台

Figure 8. Drive system experimental platform for ER-IPM hub motor

下载: 全尺寸图片幻灯片

图 9 转速为200~400 r/min在20 N·m负载下扰动实验波形

Figure 9. Speed of 200~400 r/min under 20 N·m load disturbance experiment waveform

下载: 全尺寸图片幻灯片

图 10 转速为60 r/min和负载为20 N·m下不同控制策略的稳态实验波形

Figure 10. Steady-state experimental waveforms of different control strategies under speed of 60 r/min and load of 20 N·m

下载: 全尺寸图片幻灯片

图 11 不同控制策略的变速实验波形

Figure 11. Experimental waveforms of variable speed with different control strategies

下载: 全尺寸图片幻灯片

图 12 不同控制策略的变载实验波形

Figure 12. Experimental waveforms of variable load with different control strategies

下载: 全尺寸图片幻灯片

表 1 基于不同价值函数控制策略的仿真对比结果

Table 1 Simulation results based on different cost function control strategies

控制策略	基于g₂价值函数DC-MPTC	基于g_F价值函数FWW-MPTC	降低百分比/%
转矩脉动/(N·m)	3.75	3.24	13.6
	4.53	3.77	16.8
	4.87	4.22	13.3
磁链脉动/Wb	0.019	0.016	15.8
	0.021	0.018	14.3
	0.024	0.021	12.5

下载: 导出CSV

表 2 ER-IPM轮毂电机参数

Table 2 Parameters of ER-IPM hub motor

参数	数值	参数	数值
额定转速/(r/min)	300	额定电压/V	72
额定转矩/(N·m)	40	永磁体磁链/Wb	0.047
额定功率/kW	6	极对数	25
额定电流/A	72	定子电阻/Ω	0.14
d轴电感/mH	1.272	q轴电感/mH	1.62
转动惯量/(kg·m²)	1.398	轮毂直径/cm	62

下载: 导出CSV

参考文献(31)

[1]	章恒亮, 花为. 分布式驱动系统用轮毂电机及其技术综述[J]. 中国电机工程学报, 2024, 44(7): 2871-2885. DOI: 10.13334/j.0258-8013.pcsee.222954 ZHANG Hengliang, HUA Wei. Overview of in-wheel traction machine and its key techniques for distributed-driving system[J]. Proceedings of the CSEE, 2024, 44(7): 2871-2885(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.222954
[2]	高华敏, 张卓然, 王晨, 等. 定子无铁心轴向磁场永磁轮毂电机损耗分析及效率优化[J]. 中国电机工程学报, 2021, 41(6): 2002-2011. DOI: 10.13334/j.0258-8013.pcsee.200768 GAO Huamin, ZHANG Zhuoran, WANG Chen, et al. Loss analysis and efficiency optimization of ironless stator axial flux permanent magnet in-wheel machine[J]. Proceedings of the CSEE, 2021, 41(6): 2002-2011(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.200768
[3]	李勇, 徐兴, 孙晓东, 等. 轮毂电机驱动技术研究概况及发展综述[J]. 电机与控制应用, 2017, 44(6): 1-7, 18. LI Yong, XU Xing, SUN Xiaodong, et al. Review and future development of in-wheel motor drive technology [J]. Electric Machines & Control Application, 2017, 44(6): 1-7, 18(in Chinese).
[4]	XU Lei, ZHU Xiaoyong, FAN Wenjie, et al. Comparative analysis and design of partitioned stator hybrid excitation axial flux switching PM motors for in-wheel traction applications[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 1416-1427. DOI: 10.1109/TEC.2021.3130475
[5]	ZHOU Xue, ZHU Xiaoyong, WU Wenye, et al. Multi-objective optimization design of variable- saliency-ratio PM motor considering driving cycles[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 6516-6526. DOI: 10.1109/TIE.2020.3007106
[6]	ZHANG Chao, XU Lei, ZHU Xiaoyong, et al. Elimination of DC-link voltage ripple in PMSM drives with a DC-split-capacitor converter[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8141-8154. DOI: 10.1109/TPEL.2020.3048183
[7]	刘孟楠, 雷生辉, 赵静慧, 等. 电动拖拉机发展历程与研究现状综述[J]. 农业机械学报, 2022, 53(S1): 348-364. LIU Mengnan, LEI Shenghui, ZHAO Jinghui, et al. Review of development process and research status of electric tractors[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(S1): 348-364(in Chinese).
[8]	DU Yi, HE Zhuofan, ZHU Xiaoyong, et al. A novel pole-changing permanent magnet Vernier motor[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 6110-6120. DOI: 10.1109/TIE.2022.3198237
[9]	张卓然, 陆嘉伟, 张伟秋, 等. 飞机电推进系统高效能电机及其驱动控制技术[J]. 中国电机工程学报, 2024, 44(16): 6610-6631. DOI: 10.13334/j.0258-8013.pcsee.230156 ZHANG Zhuoran, LU Jiawei, ZHANG Weiqiu, et al. High-performance electric machine and drive technologies for aircraft electric propulsion systems [J]. Proceedings of the CSEE, 2024, 44(16): 6610-6631(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.230156
[10]	WANG Zheng, CHEN Jian, CHENG Ming, et al. Field-oriented control and direct torque control for paralleled VSIs fed PMSM drives with variable switching frequencies[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2417-2428. DOI: 10.1109/TPEL.2015.2437893
[11]	孙斌, 王海霞, 苏涛, 等. 永磁同步电机调速系统非线性自抗扰控制器设计与参数整定[J]. 中国电机工程学报, 2020, 40(20): 6715-6725. DOI: 10.13334/j.0258-8013.pcsee.200018 SUN Bin, WANG Haixia, SU Tao, et al. Nonlinear active disturbance rejection controller design and tuning for permanent magnet synchronous motor speed control system[J]. Proceedings of the CSEE, 2020, 40(20): 6715-6725(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.200018
[12]	ZUO Yuefei, MEI Jie, JIANG Chaoqiang, et al. Linear active disturbance rejection controllers for PMSM speed regulation system considering the speed filter[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14579-14592. DOI: 10.1109/TPEL.2021.3098723
[13]	赵琨, 宋宝, 唐小琦, 等. 基于扩张滑模-锁相环的感应电机无速度传感器矢量控制[J]. 中国电机工程学报, 2024, 44 (20): 8270-8279. DOI: 10.13334/j.0258-8013.pcsee.231156 ZHAO Kun, SONG Bao, TANG Xiaoqi, et al. Senseless vector control method for induction motor based on extended sliding mode and phase locked loop[J]. Proceedings of the CSEE, 2024, 44(20): 8270-8279(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.231156
[14]	赵凯辉, 戴旺坷, 周瑞睿, 等. 基于扩展滑模扰动观测器的永磁同步电机新型无模型滑模控制[J]. 中国电机工程学报, 2022, 42(6): 2375-2385. DOI: 10.13334/j.0258-8013.pcsee.210273 ZHAO Kaihui, DAI Wangke, ZHOU Ruirui, et al. Novel model-free sliding mode control of permanent magnet synchronous motor based on extended sliding mode disturbance observer[J]. Proceedings of the CSEE, 2022, 42(6): 2375-2385(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.210273
[15]	黄依婷, 沈建新, 王云冲, 等. 基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制[J]. 中国电机工程学报, 2022, 42(18): 6835-6845. DOI: 10.13334/j.0258-8013.pcsee.211725 HUANG Yiting, SHEN Jianxin, WANG Yunchong, et al. Variable parameter sliding mode control of permanent magnet synchronous servo machine based on recursive least square observer[J]. Proceedings of the CSEE, 2022, 42(18): 6835-6845(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.211725
[16]	柳志飞, 杜贵平, 杜发达. 有限集模型预测控制在电力电子系统中的研究现状和发展趋势[J]. 电工技术学报, 2017, 32(22): 58-69. LIU Zhifei, DU Guiping, DU Fada. Research status and development trend of finite control set model predictive control in power electronics[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 58-69(in Chinese).
[17]	齐昕, 苏涛, 周珂, 等. 交流电机模型预测控制策略发展概述[J]. 中国电机工程学报, 2021, 41(18): 6408-6418. DOI: 10.13334/j.0258-8013.pcsee.200840 QI Xin, SU Tao, ZHOU Ke, et al. Development of AC motor model predictive control strategy: An overview[J]. Proceedings of the CSEE, 2021, 41(18): 6408-6418(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.200840
[18]	SUN Xiaodong, SHI Zhou, CAI Yingfeng, et al. Driving-cycle-oriented design optimization of a permanent magnet hub motor drive system for a four-wheel-drive electric vehicle[J]. IEEE Transactions on Transportation Electrification, 2020, 6(3): 1115-1125. DOI: 10.1109/TTE.2020.3009396
[19]	HAMMOUD I, HENTZELT S, XU Ke, et al. On continuous-set model predictive control of permanent magnet synchronous machines[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10360-10371. DOI: 10.1109/TPEL.2022.3164968
[20]	王宇, 谭国俊, 云献睿. 永磁同步电机宽速域模型预测转矩控制方法[J]. 电力电子技术, 2019, 53(10): 26-30. WANG Yu, TAN Guojun, YUN Xianrui. Model predictive torque control of PMSM over wide speed range[J]. Power Electronics, 2019, 53(10): 26-30(in Chinese).
[21]	李祥林, 薛志伟, 阎学雨, 等. 基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制[J]. 电工技术学报, 2022, 37(7): 1666-1678. LI Xianglin, XUE Zhiwei, YAN Xueyu, et al. Voltage vector rapid screening-based three-vector model predictive torque control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1666-1678(in Chinese).
[22]	张晓光, 张亮, 侯本帅. 永磁同步电机优化模型预测转矩控制[J]. 中国电机工程学报, 2017, 37(16): 4800-4809. DOI: 10.13334/j.0258-8013.pcsee.161646 ZHANG Xiaoguang, ZHANG Liang, HOU Benshuai. Improved model predictive torque control of permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(16): 4800-4809(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.161646
[23]	WU Minkai, SUN Xiaodong, ZHU Jianguo, et al. Improved model predictive torque control for PMSM drives based on duty cycle optimization[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-5.
[24]	李耀华, 陈桂鑫, 王孝宇, 等. 基于占空比调制的感应电机直接转矩控制与模型预测转矩控制研究[J]. 电机与控制应用, 2021, 48(12): 7-13. LI Yaohua, CHEN Guixin, WANG Xiaoyu, et al. Direct torque control and model predictive torque control of induction motors based on duty cycle modulation [J]. Electric Machines & Control Application, 2021, 48(12): 7-13(in Chinese).
[25]	徐艳平, 李园园, 周钦, 等. 矢量双选取的永磁同步电动机直接转矩控制策略[J]. 中国电机工程学报, 2018, 38(17): 5211-5218. DOI: 10.13334/j.0258-8013.pcsee.171814 XU Yanping, LI Yuanyuan, ZHOU Qin, et al. A double vectors selection direct torque control strategy of permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2018, 38(17): 5211-5218(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.171814
[26]	李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59, 76. LI Jiaxiang, WANG Fengxiang, KE Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59, 76(in Chinese).
[27]	梅杨, 易高. 间接矩阵变换器-异步电机调速系统模型预测控制权重系数自整定方法[J]. 电工技术学报, 2020, 35(18): 3938-3948. MEI Yang, YI Gao. A weighting factor self-tuning method in model prediction control for indirect matrix converter with induction motor system[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3938-3948.
[28]	ROJAS C A, RODRIGUEZ J, VILLARROEL F, et al. Predictive torque and flux control without weighting factors[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 681-690.
[29]	SHADMAND M B, BALOG R S, RUB H A. Auto-tuning the cost function weight factors in a model predictive controller for a matrix converter VAR compensator[C]//2015 IEEE Energy Conversion Congress and Exposition(ECCE). Montreal, QC, Canada: IEEE, 2015.
[30]	ZHANG Xiaoguang, HOU Benshuai. Double vectors model predictive torque control without weighting factor based on voltage tracking error[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2368-2380.
[31]	殷芳博, 花为, 黄文涛, 等. 基于电压矢量优化的磁通反向永磁电机模型预测转矩控制[J]. 中国电机工程学报, 2017, 37(22): 6524-6533. DOI: 10.13334/j.0258-8013.pcsee.171144 YIN Fangbo, HUA Wei, HUANG Wentao, et al. Voltage vector optimization-based model predicted torque control of flux-reversal permanent magnet machines [J]. Proceedings of the CSEE, 2017, 37(22): 6524-6533(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.171144