Evaluation of Grid-load Interactive Adjustable Capacity of Electrolytic Aluminum Load Considering Optimization of Electrolytic Cell Energy Flow
-
摘要: 电解铝负荷是典型的热蓄能高耗能工业负荷，具备良好的调节能力，充分挖掘其调节潜力，量化电解铝负荷的可调容量使其灵活参与电网互动，能够有效缓解新能源消纳、弃风弃光等问题。首先，从生产工艺角度详细分析电解槽的能量平衡机制和附加换热器的工作原理，建立电解槽的热输出控制模型。其次，基于电解槽的电热能量转换原理，由负荷的生产特性和调控约束得到负荷功率的调节边界，建立考虑电解槽能量流优化的可调容量评估模型。最后，通过模拟算例进行仿真，结果表明，通过加入附加换热器的工艺优化，使得铝厂在电解槽热平衡的能量输入和能量耗散方面均具有更强的可控性，电解铝负荷的功率调节能力得到明显提升，且功率调节的可持续时长也明显增加，显著增强了大容量电解铝参与新型电力系统网荷互动的适应性。Abstract: The electrolytic aluminum load is a typical thermal energy storage and high energy-consuming industrial load with good regulatory capabilities. By fully tapping into its regulating potential and quantifying the adjustable capacity of the electrolytic aluminum load, it can actively participate in grid interactions, effectively mitigating issues related to the integration of new energy sources and the management of wind and solar power curtailment. First, from the perspective of production processes, a detailed analysis of the energy balance mechanism of the electrolysis cells and the operating principles of additional heat exchangers is conducted. This forms the basis for establishing a thermal characteristic control model of the electrolysis cells. Then, based on the principle of electrical-thermal energy conversion in the electrolysis cells, the adjustment boundaries for load power are determined considering the production characteristics and control constraints. This leads to the development of an adjustable capacity assessment model that takes into account the optimization of energy flow within the electrolysis cells. Finally, through simulation and case studies, the results demonstrate that process optimization involving the addition of additional heat exchangers enhances the controllability of energy input and dissipation in the thermal balance of electrolysis cells. This leads to a significant improvement in the power regulation capability of the electrolytic aluminum load, along with a noticeable increase in the sustainability of power regulation. This enhancement greatly improves the adaptability of large-capacity electrolytic aluminum to participate in interactions within new-generation power grid systems.
-
0. 引言
为加快构建现代能源体系、推动能源高质量发展，《“十四五”现代能源体系规划》明确提出我国非化石能源发电量比重在2025年达到39%的目标[1]。然而新能源固有的随机性和波动性对电网的调节灵活性提出极高的要求，尤其“三北”、云南等新能源富集地区，新能源消纳压力突出、弃风弃光问题显著[2-3]。为了弥补传统发电机组调控的容量不足、成本高、响应速度慢的问题[4-5]，发展新的调控手段已成为势在必行的需求。
近年来，负荷侧的灵活可调节资源开始引起人们的广泛关注，其中，以电解铝为例的工业负荷因其容量大[6]、可控性高等特点[7]，成为电网互动调控中的重要参与者。文献[8]指出电解铝负荷饱和电抗器有功快速调节特性。文献[9]的测试结果表明，其调节速度可以比发电机快，证明电解铝负荷是提供需求响应的一种有前景的资源。文献[10-11]指出电解铝负荷功率可以在±25%的范围内连续调节，并持续运行4 h而不会导致电解槽凝槽，调节潜力巨大。文献[12]建立提供辅助服务的电解铝负荷模型，提出考虑电解铝负荷提供辅助服务的机组组合模型。文献[13]研究电解铝负荷和风力发电不确定性的源荷协调最佳调度方法。在参与调峰调频、机组组合时，电网需要电解铝负荷的可调度容量作为参考，然而电解铝负荷受到电解槽温度、电压等因素的制约[14]，不可不受控制地调度其容量。
对于可调容量的研究，目前国内外关于电动汽车、空调等一些温控负荷[15-18]的研究较多，文献[19]研究极热天气下工商业以及住宅空调负载的调节潜力，文献[20]关注到了楼宇群的高热惯性而具备的虚拟储能特性。文献[21]提出一种规模化电动汽车实时可调度容量的评估方法。文献[22]聚合了海量分散式可控资源，并研究了其调节能力的量化评估方法。对工业负荷的研究以电解类、多晶硅、矿热炉、水泥等负荷为主[23-24]。其中关于电解铝负荷可调容量的研究主要从电压和电流等生产要素出发，文献[25-26]考虑负荷生产特点与调控约束，分别从电解槽温度和电压出发建立负荷功率调节的边界条件及负荷功率调节容量定量评估模型。文献[27]考虑电解铝负荷的生产限制来约束有功功率的调节。文献[28]通过调节时间和产量对负荷调节进行约束。然而，随着电力价格的不断攀升以及铝价的变化对铝厂经营灵活性的要求，冶炼厂采取电力调控策略的财务激励越来越大，需要电解铝具有更大的可调容量范围。
在铝电解中，电解槽是基于热平衡原理设计的[29]，扩大电解铝的调节范围意味着需要对其输入功率和热损失进行大规模调整。文献[30]虽然考虑了电解槽的热平衡，但约束较为简单。文献[31-32]基于电解槽内的热平衡建立槽内电解质温度随电流强度和时间变化的动态过程，但未考虑散热的控制。目前，国内外在对电解槽的热损失控制方面已有相关研究。文献[33]研究电解槽能量平衡的两个约束，并对降低每千克铝生产能耗的目标进行了研究。基于电解槽的能量平衡，奥克兰大学轻金属研究中心研发了壳式热交换器(shell heat exchanger，SHE)技术，通过控制电解槽侧壁的热损失来平衡电解槽输入功率的变化，实现电解槽热平衡的快速调整，从而使电解槽的功率调节范围加倍[34]。文献[35]通过假设案例，研究热损失调节技术的可行性，证明这项技术可以使电解槽在输入功率大幅减少时，能够恢复和维持电解槽的能量平衡，并对电解槽无重大的不利影响。但这篇文章中对于电解铝功率削减的持续时间并没有确定的时间尺度。此外，德国和中国的学者分别对SHE技术进行了改进，并运用在冶炼厂中进行了初步的实验[36-37]，为铝的柔性生产开辟了道路。
综上，目前大部分研究主要关注的是电解槽的能量平衡，并通过实验来验证换热器技术提高电解铝负荷调节能力的可行性。然而，这些研究未能建立一个具体的模型来定量分析电解槽输出侧能量可调后的电解铝负荷可调容量，未能充分评估其调节能力。因此，本文通过详细分析电解槽的能量平衡机制和附加换热器的工作原理，构建了电解槽的热输出控制模型；其次，基于电解槽的电热能量转换原理，由负荷的生产特性和调控约束得到负荷功率的调节边界，建立考虑电解槽能量流优化的可调容量评估模型；最后，通过算例仿真验证了本文所提方法的有效性。
1. 电解槽输出侧能量可调特性分析
1.1 能量平衡分析
能量平衡在铝电解过程中起到了至关重要的作用，它不仅可以提高电流效率和技术经济指标，同时也对电解槽的稳定性和寿命起到了至关重要的作用。良好的能量平衡可以减少电解槽内部的温度梯度和热应力，从而降低因槽体膨胀而导致的机械变形和泄漏风险。因此，在铝电解过程中，实现良好的能量平衡是确保生产安全、提高产品质量和降低生产成本的关键之一。
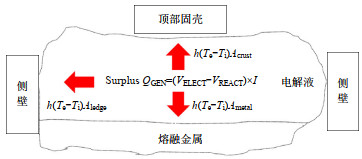
在电解槽内部，电解质的分配和流动是能量平衡的主要驱动力之一。通过对电解槽内的流动和传热机制进行深入研究，可以进一步优化电解槽结构和操作参数，从而提高能量平衡和铝电解过程的整体效率和经济性。图 1为电解槽内部能量传递的模型图，表示电解质通过对流机制分配到侧壁、熔融金属和顶部固壳的热量。
{VIN=Vde+VΩ+Van+Vca(VIN−VREACT)×I=∫Ah(Tb−Ti)dAledge+ ∫Ah(Tb−Ti)dAmetal+∫Ah(Tb−Ti)dAcrust (1) 式中：Vde为氧化铝电解反应的分解电位；VΩ为电解槽内的欧姆电压降；Van、Vca分别为阳极和阴极的过电压；VIN为这些电压分量的总和；VREACT为总的化学反应所需焓的电压当量；I为电解槽该区域的电流；h为电解质与侧壁、顶部固壳和熔融金属之间的界面i处的局部对流系数；Tb−Ti为电解质与各固体界面之间的温度差；A为电解液与固体交界面的面积。
式(1)的左边表示超出电解液反应区域所需能量的多余能量，用QGEN表示；将式(1)的右边定义为QDIST，表示熔融电解质的金属向各固体界面传递的热量；将通过电解槽外边界向环境散失的热量定义为QEXT[27]，且QDIST相当于QEXT。因此，多余能量QGEN和QEXT之间的平衡至关重要，因为这2个变量决定了上述描述的热平衡。当电解槽处于稳定状态时，3者之间呈现如式(2)的平衡。
QGEN=QDIST=QEXT (2) 对于一个可以灵活调节运行功率的电解槽，维持热平衡的关键挑战是电解槽中产生的过剩能量会随着功率的调整而发生显著的变化，需要电解槽的散热进行相匹配的改变。当输入电解槽的能量增大时，即QGEN增大时，电解质温度将根据QGEN和QDIST之间的不平衡发生变化。为了保持热平衡，需要同步增大QEXT，来消除QDIST增大时带来的不平衡，此时电解槽将从原来的稳定状态转变为另一个稳定状态，如式(3)所示。在一定的温度范围内电解槽仍然可以安全生产，稳定状态在安全范围内变化，因此电解槽总体依旧维持热平衡。
(3) 1.2 电解槽热损失分析
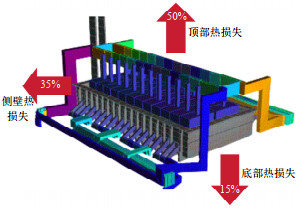
为了维持铝电解槽的热平衡，一个典型槽输入的能量约有50%以热能的形式散失到环境中，因此铝电解的能量利用率只有50%。这些热损失来自电解槽顶部烟气、侧壁和底部的散热。图 2为电解槽热量损失的示意图：热损失中的50%来自顶部烟气，35%通过电解槽的侧壁散失，剩余的15%则通过电解槽的底部散失。其中烟气中的热量占比较高，但由于温度低，回收比较困难, 因此利用价值不高。而电解槽的底部散热过于分散，也不易回收利用，因此控制电解槽侧壁的散热极为关键。
1.3 电解槽换热器原理
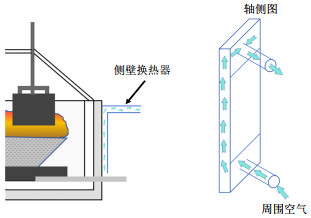
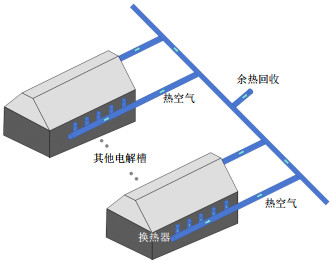
对电解槽侧壁热流的调节是通过每个安装在电解槽两侧的换热器系统来实现的，这是一种通过改变风量为侧壁提供冷却和保温的技术。单个换热器内气流路径的示意如图 3所示。
换热器由两部分组成，换热器本体和换热器进出口，换热器本体采用涡流发生器，它的作用是通过引导流体流动来增加传热表面积，并增加传热效率。图 3说明了抽风机供电的换热器的运行模式：风扇产生的真空将空气从外部附近吸入换热器入口，空气在换热器之间的缝隙向上流动，然后通过换热器顶部的开口进入与风扇相连的抽气管。
在实际生产中，当铝厂需要更高的金属产量时，即输入电解槽的能量会增加，此时换热器抽取电解槽侧壁周围的环境空气，使其进入气体管道和风扇系统中，通过改变空气的流速来改变侧壁散热的大小，以便在所需的产量和能量水平上提供可变的热量提取，防止电解槽过热。相反，当金属产量较低，即输入能量降低时，可以控制换热器，使通过热交换器的气体流量减少或完全停止，此时，热交换器在电解槽周围充当保温作用的热障层，绝缘侧壁，减少热量损失，避免电解槽温度降低导致凝槽。
2. 基于电解槽能量平衡的热输出控制模型
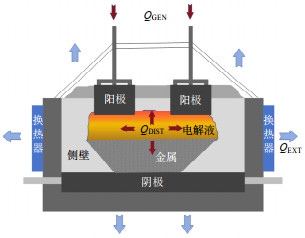
结合1.1和1.3节的内容，根据QGEN、QDIST、QEXT 3者之间的动态关系，可提出热输出控制模型：即通过调节QEXT来调节电解槽的散热，维持电解槽的热稳定性，实现电解槽对输入能量变化的动态响应，从而增大电解槽的功率调节范围。图 4为侧壁安装换热器后的QGEN、QDIST、QEXT的示意图。
结合示意图并根据3者之间的关系可以将式(1)转化为
Qin=H0+Qout (4) 式中：Qin为电解槽的能量输入；H0为总电解反应所需要的焓值；Qout为电解槽散失到环境中的热量。其中：
Qin=Pt (5) Qout=QEXT=Qtop+Qbottom+Qledge (6) 式中：Qtop为从电解槽顶部散失的热量；Qbottom为从电解槽底部散失的热量；Qledge为从电解槽侧壁散失的热量。
由于侧壁安装了换热器，实现了侧壁与空气之间的热量转换，可以有效调节该部位的散热。本文假设侧壁与空气之间的热对流过程无热量损失，则可用式(7)表示侧壁向空气对流的热量。
Qledge=hA(T−Tair)t (7) 式中：h为侧壁与空气之间的对流系数；A为换热器与侧壁的接触面积；T为侧壁的温度；Tair为空气的温度。
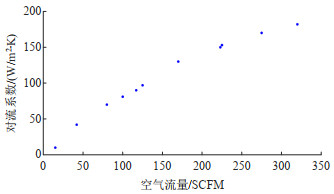
换热器-空气热对流系数h是侧壁传热回路中的一个重要参数，它决定了整个侧壁的热流，当调节进入换热器中的空气流量时，对流系数h会随着流量的改变而改变，图 5显示了不同空气流量下的对热系数，可以看出两者之间近似呈线性关系，具体的数学方程见附录式(A1)[34]。
![]()
图 5 对流系数随空气流量变化的示意图Figure 5. Schematic diagram of the convection coefficient as a function of air flow当输入能量增加时，由于QEXT可以通过可控调节的方式增加超出系统自然平衡所需的热量，因此可以平衡电解槽其他部分(顶部和底端)散热量的增加，并且考虑到底部散热占比较低，固可忽略Qtop与Qbottom。
综上可得：
Qout=QEXT=Qledge=hA(T−Tair)t (8) 进一步整理，可由式(4)、(5)、(8)得到：
Pt=H0+hA(T−Tair)t (9) 3. 电解铝负荷可调容量评估
3.1 电解槽电热能量等效转换
铝电解槽内保持良好的热平衡可减少电解过程中的能耗，而电解槽温度是表征槽内热平衡状态的重要指标，控制电解槽温度对电解铝的生产过程非常重要，需要保证电解反应在正常进行的同时，电解槽温度保持在适宜范围内，以提高生产效率和产品质量，延长设备使用寿命。
电解铝负荷有功功率的变化，会引起电解槽温度的变化，然而电解铝负荷为蓄热型负荷，热蓄能负荷的惯性时间常数大，即一段时间内的功率变化并不会对温度产生明显影响[38]。同时为了保障电解铝负荷在安全温度范围内生产，可以通过比热容公式实现电与热之间的转换, 利用热范围约束电范围。
假设在控制过程中H0不变，结合比热容公式，当输出侧的能量不可调时，可建立式(10)所示的电解槽温度与电解铝负荷调控边界的转化关系：
∫ΔPALdt=cmΔT (10) 当输出侧的能量可调，且输入能量的变化与输出侧能量的变化不匹配时，依然会引起电解槽温度的变化，由此可建立考虑输出侧能量可调的电解槽温度与电解铝负荷调控边界转化模型：
∫ΔPALdt=∫ΔQoutdt+cmΔT (11) 式中：c为熔融电解质的比热容；m为熔融电解质的质量；ΔT为电解槽温度变化量。
3.2 电解铝负荷可调容量评估方法
铝负荷正常运行时槽温一般维持在950~ 970℃，当不考虑输出侧能量可调时，电解铝负荷的最大向下和向上可调容量为：
PALmin (12) {P_{{\text{ALmax}}}} = {P_{{\text{AL}}}}(t) + ({T_{\max }} - T(t))cm/\Delta t (13) 式中Tmin、Tmax分别为生产设备温度指标的最小值和最大值。
在电解槽侧壁加入换热器装置，考虑输出侧能量可调时，通过装置的高气流可显著增强侧壁的传热能力，而低于正常生产时基本需求的气流会使侧壁隔热，从而降低传热。铝厂中的功率调节意味着提高或降低通过电解槽的线路电流强度。在较高的电流强度下，它需要散失更多的热量，而在较低的电流强度下，它需要减小散热过程中的热量。换热器的这种冷却/隔热原理使得铝厂能够通过更好地控制热损失来调节其电力使用。
由2节可知，侧壁与换热器之间的对流系数与通入换热器内的空气流量近似成正比关系，故本文以对流系数的变化代表电解铝负荷在功率调节时通入换热器中的空气流量的变化，即反映换热器的工作状态。此时换热器的调节能力也一同约束了输入功率的可调范围，则电解铝负荷的最大向下和向上可调容量可表示为：
\begin{gathered} {P_{{\text{ALmin}}}} = {P_{{\text{AL}}}}(t) + [{h_{\min }} - h(t)]A{T_{{\text{LMTD}}}} + \hfill \\ {\text{ }}cm[{T_{\min }} - T(t)]/\Delta t \hfill \\ \end{gathered} (14) \begin{gathered} {P_{{\text{ALmax}}}} = {P_{{\text{AL}}}}(t) + [{h_{\max }} - h(t)]A{T_{{\text{LMTD}}}} + \hfill \\ {\text{ }}cm[{T_{\max }} - T(t)]/\Delta t \hfill \\ \end{gathered} (15) 式中：PALmin、PALmax分别是电解铝负荷的最小调控功率和最大调控功率；PAL(t)为电解铝负荷在t时段的出力；h(t)为第t时段电解铝负荷上换热器的对流系数；hmax、hmin分别为对流系数的最大值和最小值；TLMTD为换热器与空气之间的对数平均温差，当输入功率改变时，可认为TLMTD近似不变。
4. 算例应用与分析
为了对上述计算方法进行验证, 本文模拟了一个总共有216个电解槽的铝厂，额定功率为400 MW，且电解槽的侧壁已安装换热器，安装示意图如图 6所示，其覆盖率为77%，其中对流系数的变化范围为0~120 W/m2⋅K，当对流系数为10 W/m2⋅K时，模拟的是未加换热器时电解铝负荷工作在额定情况下侧壁与周围空气间的换热情况，当对流系数低于10 W/m2⋅K时，换热器起到保温的作用。本文设置了不同场景，来评估各场景下铝厂的可调容量，时间尺度均为1 h。
![]()
图 6 安装了热交换器的电解槽示意图Figure 6. Schematic diagram of electrolytic cell with heat exchanger installed此外铝厂也充分利用通过换热器的空气的热量，冬季采暖季节用于居民供暖，而在非采暖季，这部分热量可送至火力发电厂的热循环系统，提高铝厂的能量利用率[39]。本文主要研究输入功率与换热器散热功率之间的配合。
4.1 考虑输出侧能量可控的可调容量评估
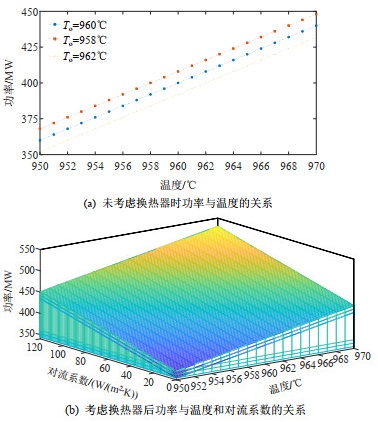
假设初始状态电解铝负荷工作在额定功率下，温度在960℃，侧壁换热器的对流系数为10 W/ m2⋅K，评估侧壁装有换热器和未装换热器两种情况下的可调容量。
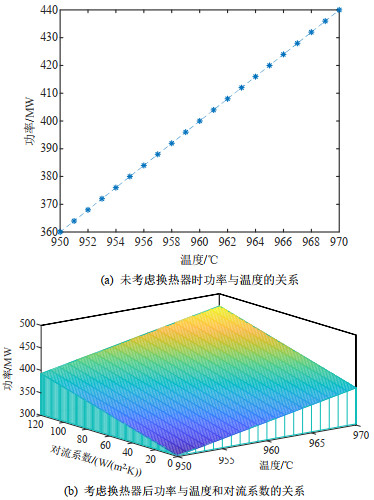
如图 7(a)所示，侧壁未装有换热器，电解铝负荷的可调范围由温度决定，随着电解铝负荷功率的增加，电解槽的温度也随之增加，当温度达到上限时，可得最大向上可调功率为440 MW；随着电解铝负荷功率的降低，电解槽的温度也从初始温度逐渐降低，当温度达到下限时，可得最大向下可调功率为360 MW，最大可调范围约为−10%~10%。
![]()
图 7 侧壁装有换热器和未装换热器的可调容量Figure 7. Adjustable capacity with and without heat exchanger on the side wall如图 7(b)所示，侧壁装有换热器，因此电解铝负荷的可调范围主要由温度和换热器的换热功率决定，当电解铝负荷的功率增加时，电解槽的温度也随之增加，由于受到温度的限制，电解铝负荷功率不能一味地增加，此时可增加通入换热器中的空气流量，提高散热功率，以此来抵消输入功率的增大，从而保证电解槽温度不越限。由于换热器散热功率的限制，可得负荷的最大可上调功率为477.494 MW；同理，当电解铝负荷功率降低时，电解槽的温度也随之下降，为了防止电解槽温度过低导致凝槽，可同步减小通入换热器中的空气流量，使换热器起到保温的作用，减少散热以抵消输入功率的降低，由此可得负荷的最大可下调功率为333.218 MW。总可调范围约为−16.69%~19.37%。
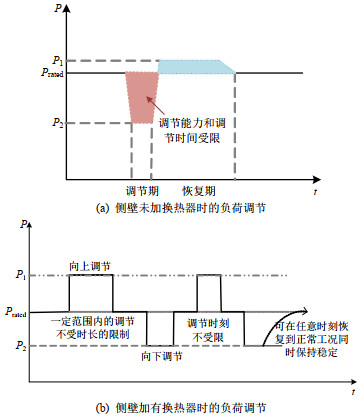
由图 8可知，在侧壁加入了换热器后，输出侧能量可控，当调节相同的功率量时，换热器能够同步调节散热功率，使得电解槽保持原来的平衡状态，并能够持续运行下去，调节时长不受限制。而未加换热器的电解槽会因长时间的功率改变使温度发生较大的变化，当调节时间过长使温度超出安全运行范围时，可能导致电解槽出现凝槽或过热的现象。同理，当调节相同的时间时，换热器的存在使得电解槽的调节能力在原有的基础上得到了提升。
![]()
图 8 侧壁装有换热器和未装换热器下的负荷调节Figure 8. Load regulation with and without heat exchanger on the side wall4.2 不同初始温度和覆盖率下的可调容量评估
假设初始状态电解铝负荷工作在额定功率下，侧壁换热器的对流系数为10 W/m2⋅K，评估侧壁装有换热器和未装换热器在不同初始温度下的可调容量。
如图 9(a)所示，当电解槽处于同一温度时，初始温度高的电解铝负荷，其功率最大可上调裕度减小，而最大可下调裕度在增加。
![]()
图 9 不同初始温度和覆盖率下可调容量对比Figure 9. Comparison of adjustable capacity at different initial temperatures and coverage rates如图 9(b)所示，当电解槽处于同一温度且换热器工作功率一致时，初始温度高的电解铝负荷，其功率最大可上调裕度减小，而最大可下调裕度在增加。同理，当改变换热器的初始工作功率时，同一温度下，电解铝负荷的最大可上调裕度随其初始工作功率的增加而减少，而最大可下调裕度则在增加。
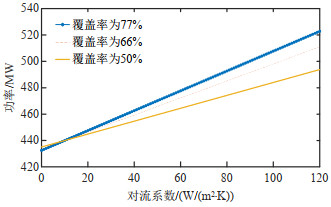
改变侧壁换热器的覆盖率，比较不同覆盖率下负荷的最大向上可调节量。由图 10可知，当对流系数大于10 W/m2⋅K时，随着换热器覆盖率的增加，侧壁的传热能力提高，当输入功率增加时，散热能力也更强，因此相同的换热功率下，覆盖率大的可调节量多；同理，当对流系数小于10 W/m2⋅K时，换热器覆盖率高的侧壁保温能力也更强，所以向下可调节能力也增强。
![]()
图 10 不同覆盖率下功率与对流系数的关系Figure 10. Relationship between power and convection coefficient under different coverages4.3 网荷互动模式下电解铝负荷可调能力评估
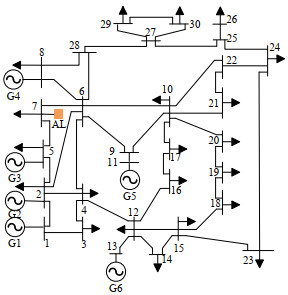
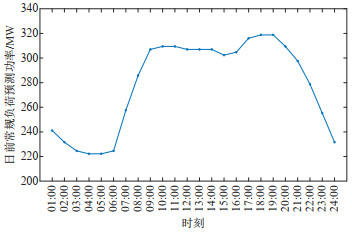
为了进一步验证本文所提模型的有效与合理性，在改进的IEEE-30节点系统进行日前时段的仿真与分析。改进后的IEEE-30节点系统中含有6台火电机组，总容量为1 190 MW，如图 11所示，分别接于节点1、节点2、节点5、节点8、节点11、节点13，电解铝负荷接在7号节点，总功率为400 MW，机组参数如附表 A1所示。调度周期为24 h，间隔为1 h。针对此算例，本文在MATLAB软件中运行，通过YALMIP工具箱调用优化软件CPLEX进行求解。日前常规负荷预测功率值如附图 A1所示。以最小化系统运行成本为目标函数，具体模型如下：
1）目标函数。
\min F = {F_1} + {F_2} (16) \left\{\begin{array}{l} {F_1} = \sum\limits_{i = 1}^n {\sum\limits_{t = 1}^T {{u_{i,t}}({a_i}{{(P_{i,t}^{{\text{th}}})}^2} + {b_i}P_{i,t}^{{\text{th}}} + {c_i})} } \hfill \\ {F_2} = \sum\limits_{i = 1}^n {\sum\limits_{t = 1}^T {{u_{i,t}}(1 - {u_{i,t - 1}})S_{i,t}^{\text{U}} + } } \hfill \\ {\text{ }}\sum\limits_{i = 1}^n {\sum\limits_{t = 1}^T {{u_{i,t - 1}}(1 - {u_{i,t}})S_{i,t}^{\text{D}}} } \hfill \\ \end{array}\right. (17) 2）约束条件。
模型的约束条件包括系统功率平衡约束、火电机组出力约束、爬坡约束、启停约束、启停成本约束、直流潮流约束，具体形式见附录式(A2)—(A8)。电解铝负荷相关约束如式(18)所示。
\left\{\begin{array}{l} {T_{\min }} \leqslant {T_t} \leqslant {T_{\max }} \hfill \\ {h_{\min }} \leqslant {h_t} \leqslant {h_{\max }} \hfill \\ P_{t,\min }^{{\text{AL}}} \leqslant P_t^{{\text{AL}}} \leqslant P_{t,\max }^{{\text{AL}}} \hfill \\ \end{array}\right. (18) 式中：F1为火电机组的燃料成本；F2为火电机组的启停成本； P_{i,t}^{{\text{th}}} 为火电机组i在t时段的出力；ai、bi、ci为燃料成本系数；ui, t为火电机组开停机状态的0-1变量，0表示关机状态、1表示开机状态； S_{i,t}^{\text{U}} 和 S_{i,t}^{\text{D}} 分别为火电机组i在t时段的开停机成本系数； P_t^{{\text{AL}}} 为t时段铝的功率。
假设初始状态电解铝负荷工作在额定功率下，温度在960℃，侧壁换热器的对流系数为10 W/ m2⋅K，对比侧壁装有换热器和未装换热器两种情况下的负荷调节情况。
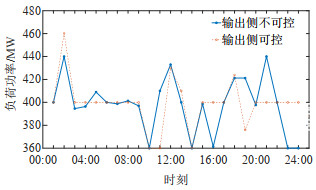
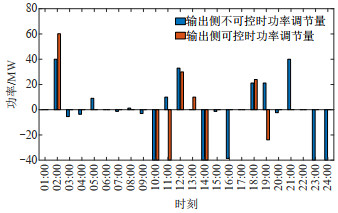
图 12和13分别展示了两种情况下电解铝负荷的出力与功率调节量的对比结果。可见在网荷互动模式下，输出侧能量可控的电解铝负荷能够提供更多的调节能力，最大向上调节量可达60.17 MW，而输出侧能量不可控时，最大向上调节量为39.86 MW。
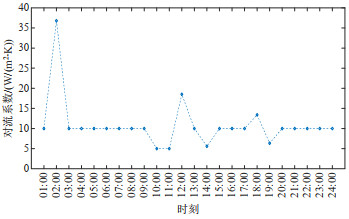
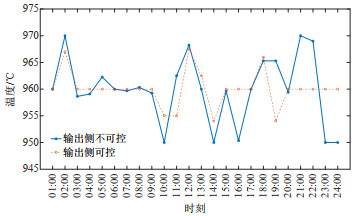
图 14和15分别为换热器的工作情况以及两种情况下电解槽的温度变化示意图。对比图 12和15，输出侧能量不可控的情况中，在温度的约束下，当电解槽的温度达到临界点时，电解铝负荷的调节量也达到极限。当输出侧能量可控时，电解槽的温度在954~966℃范围内变化，且温度曲线变化相对更加平稳，没有频繁波动。这是因为，当电解铝负荷功率增加时，电解槽的温度也会增加，此时增大通入换热器中的空气流量，传热系数变大，换热器功率同步增大，限制了电解槽的温度变化。同理，当负荷功率下降时，侧壁的换热器起到保温的作用，防止电解槽温度持续下降，对电解槽起到了保护作用。对比图 12和14可以发现，换热器工作状态的变化趋势与负荷功率的变化趋势一致，具有较强的灵活调节能力。
5. 结论
本文首先分析了电解槽的能量平衡机制和换热器工作原理，并在此基础上建立了电解槽的热输出控制模型，考虑负荷的生产特点和调控约束得到负荷功率调节的边界，建立了考虑电解槽能量流优化的可调容量评估模型。通过模拟算例，评估了不同场景下电解铝负荷的可调容量。结果如下：
1）考虑输出侧能量可控的情况下电解铝负荷的可调能力大幅提高，同时一定范围内的调节不受持续时长的限制。
2）改变电解槽的初始温度，随着初始温度的升高，电解铝负荷的最大可上调功率随之减少，而最大可下调功率在增加；改变换热器的覆盖率，随着侧壁换热器覆盖率的提高，侧壁的散热和保温能力均得到提升，输入功率可调范围增大。
3）网荷互动模式下，考虑输出侧能量可控的电解铝负荷能够及时的根据输入功率的变化调整散热功率，电解槽的温度变化较为平稳，对电解槽起到了保护作用，可调能力得到了提高。
综上所述，通过引入电解槽的换热器控制技术，可以实现对电解铝负荷的灵活控制，从而根据电网的实际需求，对电解铝负荷进行调整，以实现最优的调节效果，为电力系统的稳定性和可持续性提供了重要的支持。该评估方法可为电解铝负荷深度且安全的参与电网互动控制提供理论计算的参考依据。
附录A
强制对流换热系数预测方程：
\frac{{h{D_{\text{e}}}}}{K} = 0.023{(\frac{{{D_{\text{e}}}V\rho }}{\mu })^{0.8}}{(\frac{{{C_{\text{p}}}\mu }}{K})^{0.33}} (A1) 式中：h为对流系数；De为与换热器尺寸相同的矩形管道的直径；V为管道内的表面气流速度；ρ为空气密度；μ为空气黏度；Cp为空气的比热容；K为空气的导热系数。
A1 火电机组部分运行参数A1. Selected operating parameters of thermal power units机组 Pmin/MW Pmax/MW a/(元/(MW⋅h2)) b/(元/(MW⋅h)) c/(元/h) G1 125 390 0.152 4 38.539 7 786.798 8 G2 62.5 250 0.105 8 46.159 1 945.633 2 G3 37.5 150 0.028 0 40.396 5 1 049.997 7 G4 50 200 0.035 4 38.305 5 1 243.531 1 G5 25 100 0.021 1 36.327 8 1 685.569 6 G6 25 100 0.017 9 38.270 4 1 365.659 2 式(A1)为系统功率平衡约束，式(A2)为火电出力约束，式(A3)为爬坡约束，式(A4)为启停约束，式(A5)、(A6)为启停成本约束，式(A7)为直流潮流约束。
\sum\limits_{i = 1}^n {P_{i,t}^{{\text{th}}}} = P_t^{{\text{load}}} + P_t^{{\text{AL}}} (A2) {u_{i,t}}P_{i,\min }^{{\text{th}}} \leqslant P_{i,t}^{{\text{th}}} \leqslant {u_{i,t}}P_{i,\max }^{{\text{th}}} (A3) \left\{\begin{array}{l} P_{i,t - 1}^{{\text{th}}} - P_{i,t}^{{\text{th}}} \leqslant {V_{{\text{D}},i}}{u_{i,t}} + {S_{{\text{D}},i}}({u_{i,t - 1}} - {u_{i,t}}) + P_{i,\max }^{{\text{th}}}(1 - {u_{i,t - 1}}) \hfill \\ P_{i,t}^{{\text{th}}} - P_{i,t - 1}^{{\text{th}}} \leqslant {V_{{\text{U}},i}}{u_{i,t - 1}} + {S_{{\text{U}},i}}({u_{i,t}} - {u_{i,t - 1}}) + P_{i,\max }^{{\text{th}}}(1 - {u_{i,t}}) \hfill \\ \end{array}\right. (A4) \left\{\begin{array}{l} (T_{i,t - 1}^{{\text{on}}} - T_{i,\min }^{{\text{on}}})({u_{i,t - 1}} - {u_{i,t}}) \geqslant 0 \hfill \\ (T_{i,t - 1}^{{\text{off}}} - T_{i,\min }^{{\text{off}}})({u_{i,t}} - {u_{i,t - 1}}) \geqslant 0 \hfill \\ \end{array}\right. (A5) \left\{\begin{array}{l} C_{i,t = 1}^{\text{U}} \geqslant S_i^{\text{U}}({u_{i,t = 1}} - u_i^0) \hfill \\ C_{i,t}^{\text{U}} \geqslant S_i^{\text{U}}({u_{i,t}} - {u_{i,t - 1}}) \hfill \\ C_{i,t}^{\text{U}} \geqslant 0 \hfill \\ \end{array}\right. (A6) \left\{\begin{array}{l} C_{i,t = 1}^{\text{D}} \geqslant S_i^{\text{D}}(u_i^0 - {u_{i,t = 1}}) \hfill \\ C_{i,t}^{\text{D}} \geqslant S_i^{\text{D}}({u_{i,t - 1}} - {u_{i,t}}) \hfill \\ C_{i,t}^{\text{D}} \geqslant 0 \hfill \\ \end{array}\right. (A7) \left|\boldsymbol{T}_{\mathrm{F}}\left(\boldsymbol{K}^{\mathrm{th}} \boldsymbol{P}^{\mathrm{th}}-\boldsymbol{K}^{\mathrm{ld}} \boldsymbol{P}^{\mathrm{ld}}-\boldsymbol{K}^{\mathrm{AL}} \boldsymbol{P}^{\mathrm{AL}}\right)\right| \leq \boldsymbol{P}_{\mathrm{L}, \text { max }} (A8) 式中： P_{i,t}^{{\text{th}}} 为火电机组i在t时段的出力； P_t^{{\text{AL}}} 为t时段铝的功率；ui, t为火电机组开停机状态的0-1变量，0表示关机状态、1表示开机状态； P_{i,\min }^{{\text{th}}} 、 P_{i,\max }^{{\text{th}}} 分别为机组i的最小、最大出力限制；VU, i、VD, i分别为第i台机组的向上、向下爬坡速率；SU, i、SD, i分别为第i台机组的开机、停机爬坡速率； T_{i,t}^{{\text{on}}} 、 T_{i,t}^{{\text{off}}} 分别为机组i在t时段的连续开机、停机时间； T_{i,\min }^{{\text{on}}} 、 T_{i,\min }^{{\text{off}}} 分别为机组i的最小开机、停机时间； C_{i,t}^{\text{U}} 、 C_{i,t}^{\text{D}} 分别为机组i的开停机成本；TF为转移因子矩阵；Kth、Kld、KAL分别为火电及负荷潮流分布系数矩阵；Pth为火电注入向量；Pld、PAL为负荷需求向量；PL, max为线路潮流约束向量。
-
![]()
图 5 对流系数随空气流量变化的示意图
Figure 5. Schematic diagram of the convection coefficient as a function of air flow
![]()
图 6 安装了热交换器的电解槽示意图
Figure 6. Schematic diagram of electrolytic cell with heat exchanger installed
![]()
图 7 侧壁装有换热器和未装换热器的可调容量
Figure 7. Adjustable capacity with and without heat exchanger on the side wall
![]()
图 8 侧壁装有换热器和未装换热器下的负荷调节
Figure 8. Load regulation with and without heat exchanger on the side wall
![]()
图 9 不同初始温度和覆盖率下可调容量对比
Figure 9. Comparison of adjustable capacity at different initial temperatures and coverage rates
![]()
图 10 不同覆盖率下功率与对流系数的关系
Figure 10. Relationship between power and convection coefficient under different coverages
A1 火电机组部分运行参数
A1 Selected operating parameters of thermal power units
机组 Pmin/MW Pmax/MW a/(元/(MW⋅h2)) b/(元/(MW⋅h)) c/(元/h) G1 125 390 0.152 4 38.539 7 786.798 8 G2 62.5 250 0.105 8 46.159 1 945.633 2 G3 37.5 150 0.028 0 40.396 5 1 049.997 7 G4 50 200 0.035 4 38.305 5 1 243.531 1 G5 25 100 0.021 1 36.327 8 1 685.569 6 G6 25 100 0.017 9 38.270 4 1 365.659 2 
下载: 导出CSV
-
[1] 贺觉渊. 可再生能源发电2035年将成为主体电源[N]. 证券时报, 2022-03-23(A01). HE Jueyuan. Renewable power generation will become the main power source by 2035[N]. Securities Times, 2022-03-23(A01)(in Chinese).
[2] 舒印彪, 张智刚, 郭剑波, 等. 新能源消纳关键因素分析及解决措施研究[J]. 中国电机工程学报, 2017, 37(1): 1-8. SHU Yinbiao, ZHANG Zhigang, GUO Jianbo, et al. Study on key factors and solution of renewable energy accommodation[J]. Proceedings of the CSEE, 2017, 37(1): 1-8(in Chinese).
[3] 王云珠. 我国可再生能源消纳制约因素分析及解决对策[J]. 煤炭经济研究, 2020, 40(2): 4-11. WANG Yunzhu. Analysis of restrictive factors on renewable energy consumption in China and countermeasures[J]. Coal Economic Research, 2020, 40(2): 4-11(in Chinese).
[4] 任景, 薛晨, 马晓伟, 等. 源荷联动调峰辅助服务市场两阶段模型[J]. 电力系统自动化, 2021, 45(18): 94-102. REN Jing, XUE Chen, MA Xiaowei, et al. Two-stage model of peak regulation ancillary service market with source-load interaction[J]. Automation of Electric Power Systems, 2021, 45(18): 94-102(in Chinese).
[5] 刘闯, 孙傲, 王艺博, 等. 计及电熔镁负荷与储能联合调峰的电力系统日前-日内联合经济调度方法[J]. 电力自动化设备, 2022, 42(2): 8-15. LIU Chuang, SUN Ao, WANG Yibo, et al. Day-ahead and intra-day joint economic dispatching method of electric power system considering combined peak-shaving of fused magnesium load and energy storage[J]. Electric Power Automation Equipment, 2022, 42(2): 8-15(in Chinese).
[6] 王勇, 仲维洋, 佟永吉, 等. 电解铝企业参与弃风消纳可行性与经济性分析[J]. 轻金属, 2021(1): 58-62. WANG Yong, ZHONG Weiyang, TONG Yongji, et al. Feasibility and economic analysis of aluminum enterprises participating in wind curtailment accommodation[J]. Light Metals, 2021(1): 58-62(in Chinese).
[7] LIAO Siyang, XU Jian, SUN Yuanzhang, et al. Control of energy-intensive load for power smoothing in wind power plants[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6142-6154. DOI: 10.1109/TPWRS.2018.2834940
[8] AGUERO J L, BEROQUI M, ACHILLES S. Aluminum plant. Load modeling for stability studies[C]//Proceedings of the IEEE Power Engineering Society Summer Meeting. Edmonton: IEEE, 1999: 1330-1335.
[9] LIAO Siyang, XU Jian, SUN Yuanzhang, et al. Local utilization of wind electricity in isolated power systems by employing coordinated control scheme of industrial energy-intensive load[J]. Applied Energy, 2018, 217: 14-24. DOI: 10.1016/j.apenergy.2018.02.103
[10] PAULUS M, BORGGREFE F. The potential of demand-side management in energy-intensive industries for electricity markets in Germany[J]. Applied Energy, 2011, 88(2): 432-441. DOI: 10.1016/j.apenergy.2010.03.017
[11] BABU C A, ASHOK S. Peak load management in electrolytic process industries[J]. IEEE Transactions on Power Systems, 2008, 23(2): 399-405. DOI: 10.1109/TPWRS.2008.920732
[12] LIU Jianing, ZENG Kaiwen, WANG Chenglong, et al. Unit commitment considering electrolytic aluminum load for ancillary service[C]//4th International Conference on Intelligent Green Building and Smart Grid(IGBSG). Hubei, China: IEEE, 2019: 608-611.
[13] LIU Jianing, WANG Ke, SU Zhuo, et al. Source-load coordinated optimal scheduling in stochastic unit commitment considered electrolytic aluminum load and wind power uncertainty[C]//5th International Electrical and Energy Conference(CIEEC). Nanjing, China: IEEE, 2022: 2175-2179.
[14] YU Qingfang, XU Jian, LIAO Siyang, et al. Adaptive load control of electrolytic aluminum for power system frequency regulation based on the aluminum production operation state[J]. Energy Reports, 2022, 8: 1259-1269. DOI: 10.1016/j.egyr.2022.02.203
[15] 周椿奇, 向月, 童话, 等. 轨迹数据驱动的电动汽车充电需求及V2G可调控容量估计[J]. 电力系统自动化, 2022, 46(12): 46-55. ZHOU Chunqi, XIANG Yue, TONG Hua, et al. Trajectory-data-driven estimation of electric vehicle charging demand and vechicle-to-grid regulable capacity [J]. Automation of Electric Power Systems, 2022, 46(12): 46-55(in Chinese).
[16] YANG Xingang, LIU Jiayu, ZHOU Jian, et al. Evaluation of air-conditioning load adjustability based on load plasticity[J]. Journal of Physics: Conference Series, 2021, 1920: 012055. DOI: 10.1088/1742-6596/1920/1/012055
[17] SONG Meng, SUN Wei. Applications of thermostatically controlled loads for demand response with the proliferation of variable renewable energy[J]. Frontiers in Energy, 2022, 16(1): 64-73. DOI: 10.1007/s11708-021-0732-5
[18] ZHANG Shuzhi, ZHANG Xiongwen. A multi time-scale framework for state-of-charge and capacity estimation of lithium-ion battery under optimal operating temperature range[J]. Journal of Energy Storage, 2021, 35: 102325. DOI: 10.1016/j.est.2021.102325
[19] LU Liang, WEI Mingkui, ZHANG Peng, et al. Load adjustable potential assessment considering load flexible control and air conditioner load response in extremely hot weather[C]//8th International Conference on Power and Renewable Energy(ICPRE). Shanghai, China: IEEE, 2023: 1505-1510.
[20] 唐文虎, 张银, 钱瞳. 考虑配电网络重构和楼宇群主动需求响应的集成楼宇群配电网优化控制[J]. 中国电机工程学报, 2023, 43(8): 2966-2978. TANG Wenhu, ZHANG Yin, QIAN Tong. Optimal control of buildings-to-distribution-network integration system considering reconfiguration of distribution network and active demand response of buildings[J]. Proceedings of the CSEE, 2023, 43(8): 2966-2978(in Chinese).
[21] 张聪, 张祥文, 夏俊荣, 等. 电动汽车实时可调度容量评估方法研究[J]. 电力系统保护与控制, 2015, 43(22): 99-106. ZHANG Cong, ZHANG Xiangwen, XIA Junrong, et al. Research on estimation of electric vehicles real-time schedulable capacity[J]. Power System Protection and Control, 2015, 43(22): 99-106(in Chinese).
[22] 薛景润, 施啸寒, 王超, 等. 兼顾物理状态和用户行为的虚拟电厂紧急功率调节能力量化评估[J]. 中国电机工程学报, 2023, 43(8): 2906-2920. XUE Jingrun, SHI Xiaohan, WANG Chao, et al. Online evaluation of emergency power regulation capability for virtual power plants considering physical characteristics and user behavior constraints[J]. Proceedings of the CSEE, 2023, 43(8): 2906-2920(in Chinese).
[23] 范宇辉, 姜婷玉, 黄奇峰, 等. 基于画像的工业园区需求响应潜力评估[J]. 电力系统自动化, 2024, 48(1): 41-49. FAN Yuhui, JIANG Tingyu, HUANG Qifeng, et al. Portrait-based assessment on demand response potential of industrial parks[J]. Automation of Electric Power Systems, 2024, 48(1): 41-49(in Chinese).
[24] 蒋雪怡, 徐箭, 廖思阳, 等. 考虑工业用户响应意愿差异性的工业园区多类型负荷协同平抑风电功率波动控制方法[J]. 武汉大学学报: 工学版, 2022, 55(9): 876-885. JIANG Xueyi, XU Jian, LIAO Siyang, et al. Coordinated control scheme of multi-type loads for wind power fluctuation in industrial parks considering the difference in response willingness of industrial users[J]. Engineering Journal of Wuhan University, 2022, 55(9): 876-885(in Chinese).
[25] 徐箭, 余青芳, 廖思阳, 等. 考虑生产安全的工业园区联络线功率平滑策略[J]. 上海交通大学学报, 2024, 58(6): 941-953. XU Jian, YU Qingfang, LIAO Siyang, et al. Power smoothing strategy for industrial park tie-line considering production safety[J]. Journal of Shanghai Jiao Tong University, 2024, 58(6): 941-953(in Chinese).
[26] BAO Peng, ZHANG Wen, CHENG Dingyi, et al. Hierarchical control of aluminum smelter loads for primary frequency support considering control cost[J]. International Journal of Electrical Power & Energy Systems, 2020, 122: 106202. http://www.sciencedirect.com/science/article/pii/S0142061520301927
[27] 骆钊, 聂灵峰, 田肖, 等. 基于模型预测控制的电解铝负荷参与电网频率稳定控制策略[J]. 电力建设, 2023, 44(10): 1-11. LUO Zhao, NIE Lingfeng, TIAN Xiao, et al. Control strategy of electrolytic aluminum load participating in power network frequency stability based on model predictive control[J]. Electric Power Construction, 2023, 44(10): 1-11(in Chinese).
[28] 张斌, 司大军, 李凡, 等. 计及电解铝负荷需求侧响应的风电并网调峰研究[J]. 电工电能新技术, 2023, 42(7): 31-38. ZHANG Bin, SI Dajun, LI Fan, et al. Research on peak shaving of wind power grid connection considering demand side response of electrolytic aluminum load[J]. Advanced Technology of Electrical Engineering and Energy, 2023, 42(7): 31-38(in Chinese).
[29] LIU Jingjing, TAYLOR M, DORREEN M. Dynamic response of cryolitic bath and influence on cell heat and mass balance with large scale potline power shifts[M]// WILLIAMS E. Light Metals 2016. Cham: Springer, 2016: 601-605.
[30] 陈光宇, 杨锡勇, 江海洋, 等. 高比例新能源接入下计及工业负荷特性的电网需求响应调控策略[J]. 电力自动化设备, 2023, 43(4): 177-184. CHEN Guangyu, YANG Xiyong, JIANG Haiyang, et al. Demand response regulation strategy for power grid accessed with high proportion of renewable energy considering industrial load characteristics[J]. Electric Power Automation Equipment, 2023, 43(4): 177-184(in Chinese).
[31] 王成龙. 计及电解铝负荷参与需求响应的电力系统低碳经济调度[D]. 武汉: 华中科技大学, 2022. WANG Chenglong. Low-carbon economic dispatch of power system considering electrolytic aluminum load for demand response[D]. Wuhan: Huazhong University of Science and Technology, 2022(in Chinese).
[32] HUANG Yongbo, DU Shanzhou, LU Guoping, et al. Electrothermal decoupling method for aluminum electrolyzer considering heat supply from CHP unit[C]// 2023 3rd Power System and Green Energy Conference (PSGEC). Shanghai: IEEE, 2023: 1064-1069.
[33] TAYLOR M P, ETZION R, LAVOIE P, et al. Energy balance regulation and flexible production: a new frontier for aluminum smelting[J]. Metallurgical and Materials Transactions E, 2014, 1(4): 292-302. DOI: 10.1007/s40553-014-0029-2
[34] LAVOIE P, NAMBOOTHIRI S, DORREEN M, et al. Increasing the power modulation window of aluminium smelter pots with shell heat exchanger technology[M]// LINDSAY S J. Light Metals 2011. Cham: Springer, 2011: 369-374.
[35] TAYLOR M P, CHEN J J J. Technique for low amperage potline operation for electricity grid storage [J]. Metallurgical and Materials Transactions E, 2015, 2(1): 87-98. http://www.onacademic.com/detail/journal_1000037441249210_c7ea.html
[36] DORREEN M, WRIGHT L, MATTHEWS G, et al. Transforming the way electricity is consumed during the aluminium smelting process[M]//ZHANG Lei, DRELICH J W, NEELAMEGGHAM N R, et al. Energy Technology 2017. Cham: Springer, 2017: 15-25.
[37] LIANG Xuemin. Optimization of thermal characteristics and "output side energy saving" of aluminum reduction cell[M]//PERANDER L. Light Metals 2021. Cham: Springer, 2021: 325-332.
[38] 廖思阳. 高耗能负荷参与高渗透率风电孤立电网频率控制方法研究[D]. 武汉: 武汉大学, 2016. LIAO Siyang. Research on participation of energy-intensive load in frequency regulation in isolated power system with high penetration of wind power [D]. Wuhan: Wuhan University, 2016(in Chinese).
[39] 梁学民, 冯冰, 曹志成, 等. 铝电解槽双端节能理论及工业应用[J]. 中国有色金属学报, 2023, 33(3): 850-861. LIANG Xuemin, FENG Bing, CAO Zhicheng, et al. Aluminum electrolytic cell double-ports energy-saving theory and industrial application[J]. The Chinese Journal of Nonferrous Metals, 2023, 33(3): 850-861(in Chinese).
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
下载:
