0.   引言

能源转型的迫切需求推动了以风能为代表的新能源发电技术的快速发展^[1-2]。根据国家发展改革委、国家能源局等9部门联合印发的《“十四五”可再生能源发展规划》，2035年，我国风电和太阳能发电总装机容量将达到12亿kW以上。在双碳目标的推动下，风电装机容量还将进一步提升。风机大量接入电网替代同步机组将导致系统频率响应特性变差，抗功率扰动能力下降，频率安全问题突出^[3-4]。从稳态充裕性角度出发，要求备用总量大于功率扰动(源荷波动、N−1故障等)的备用留取方式已不再适用于高新能源占比的新型电力系统^[5]。

一方面，在备用方案制定过程中引入频率安全约束，以确保系统留取充足的一次调频备用(primary frequency reserve，PFR)是保证系统频率安全的有效手段。文献[6]假设机组一次调频备用随时间线性增发，并忽略负荷频率特性，推导频率稳定的充分条件；文献[7]在文献[6]的基础上考虑储能对系统频率稳定的支撑作用；文献[8]在文献[6]的基础上考虑负荷频率特性的影响，推导频率稳定的充分条件；文献[9]基于线性爬坡假设建立系统频率响应模型，考虑关键机组N−1故障进行备用优化；文献[10]从传递函数出发，推导频率稳定指标的时域表达式，并利用超平面分段线性化处理频率稳定约束。

另一方面，随着风电渗透率的逐步提高，传统同步机组逐步退出运行，系统对运行备用的需求不断增加，而常规调节资源的占比却不断减少。传统电力系统调度中，为充分利用风能，风机一般以最大功率点跟踪(maximum power point tracking，MPPT)方式运行，不具备灵活调节能力。随着风机控制技术的发展，风机可以通过超速控制提供PFR以缓解系统备用压力^[11]，因此亦有相关研究挖掘风机的频率支撑能力。文献[12]同时考虑火电、水电和风电对系统频率的支撑作用，建立两阶段随机备用优化模型；文献[13]在备用决策中同时考虑风机的惯量支撑和一次调频能力；文献[14]进一步考虑风机惯量支撑的不确定性；文献[15]基于机会约束随机优化，建立考虑风储系统提供频率支撑的两阶段备用优化模型；文献[16]从传递函数出发推导频率稳定约束，分段线性化处理后添加到风电稳态备用优化模型中，但未充分考虑风电提供频率支撑对应的PFR。

相关专家学者在风电参与频率支撑的备用优化方面已开展大量研究，但仍存在以下两方面的问题。

一是上述文献均认为风机的备用能力只受到风速和其他气象条件等外生不确定性因素影响。但当风机通过超速控制降载运行以提供PFR时，其转速决策会影响风机的风能捕获系数，从而影响风电并网功率和PFR功率。因此，风电功率和风电PFR的不确定性不仅和风速有关，也和转速这一决策变量有关。在建模风机的一次调频备用时，若忽略这一决策依赖关系，则无法考虑和转速决策有关的物理约束，导致模型无法充分反应风机实际运行工况。

二是现有关于风机通过超速控制提供频率支撑的研究均假设风机转速在MPPT转速和最大转速之间全范围可调。但受到感应发电机效应的影响，当风机运行在某一转速区间时，系统等值电阻为负^[17]，可能会造成双馈风机发生次同步功率振荡。若在安排风电场出力和备用计划时忽视这一转速区间的影响，可能会导致实际运行过程中发生次同步振荡，威胁系统安全稳定运行。本文将该转速区间称之为风机禁止转速区间，其含义可类比传统火力发电机组的禁止运行区间^[18]，但前者为转速区间，后者通常为功率区间。

本文以双馈风机为研究对象，针对风电和火电协同提供一次调频备用，开展两方面研究：一是分析风电一次调频备用中的决策依赖不确定性，以及禁止转速区间对风电一次调频备用的影响，并重新定义部分工况下的弃风功率；二是基于两阶段随机优化，建立计及决策依赖不确定性和禁止转速区间的频率约束风火协同备用优化模型，并给出线性化处理方法，算例验证所提模型和方法的有效性。

1.   风电一次调频备用的决策依赖不确定性

双馈风机的输出功率P_w由桨距角、转速、风速大小以及风机物理结构共同决定^[19]：

式中：ρ为空气密度；r为风机叶片半径；V_w为风速；C_p(λ, β)为风能捕获系数；λ为风机叶尖速比；β为桨距角；$\bar \lambda$为公式化简中间变量。

当风机采用MPPT控制，桨距角设置为0，转速则根据风速变化而调整，以获得最优的叶尖速比和最大风能捕获系数，此时风机无法提供备用支撑。当采用超速控制或变桨距角控制使风机的输出功率偏离最大功率点，风机则具备提供备用支撑的能力。前者控制风机转速大于MPPT转速，从而降低风力机组的风能捕获效率，当需要增加输出功率时，再控制转速降低趋近于最优转速使风机捕获更多风功率^[11]；后者则是增加风机的桨距角以减小风机捕获的风功率，其桨距角调节裕度即对应备用功率^[20]。

超速控制基于交流变频控制技术，控制速度远比变桨距角控制快。变桨距角控制的执行机构为机械部件，控制速度慢，频率支撑效果不明显，且变桨系统的频繁动作将加剧机械损耗，增加检修费用，缩短风机使用寿命。因此本文考虑风机通过超速控制提供备用支撑，桨距角设置为0。因此风机的风能捕获系数可以表示为风速和风机转速的函数，如式(2)所示，其中f¹()对应式(1)所表达的函数关系。

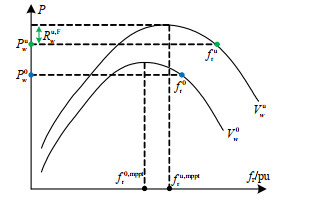
图 1为日前-日内两阶段调度框架下，风机超速控制提供一次调频备用示意图。日前阶段，风速和风机转速分别为$V_w^0$和$f_{\text{r}}^0$；日内阶段，根据不确定性风速场景$V_w^{\text{u}}$以及一次调频备用需求，风机转速调整为$f_{\text{r}}^{\text{u}}$，和MPPT转速$f_{\text{r}}^{{\text{u, mppt}}}$之间的转速调节裕度对应风机提供的一次调频备用$R_w^{{\text{u, F}}}$，如式(3)和(4)所示。式(5)表示风机转速需大于MPPT转速，小于最大转速$f_{\text{r}}^{{\text{u}}, \max }$。

图  1  风机通过超速控制提供一次调频备用

Figure  1.  Wind turbine provides primary frequency reserve through overspeed control

下载: 全尺寸图片 幻灯片

可见，风机能够提供的一次调频备用的不确定性不仅和风速不确定性有关，而且受到风机转速这一决策变量的影响，这也是本文模型中决策依赖不确定性的来源。

2.   禁止转速区间定义及其对风电备用的影响

2.1   禁止转速区间定义

禁止转速区间定义：为保证系统安全稳定运行而应避开的转速运行点集合。

根据模型应用场景(应包含风机转速这一控制变量)的不同，禁止转速区间可基于不同的电力系统安全稳定机理进行推导。下文从次同步谐振的感应发电机效应原理出发，简述在次同步谐振这一特定场景下，禁止转速区间的推导过程，并结合风机超速控制，建立计及决策依赖不确定性和禁止转速区间的备用优化模型。需要说明的是，本文研究仍聚焦于备用优化调度，安全稳定机理并非本文重点。后续建立的备用优化模型只需禁止转速区间这一结果作为输入，而并不依赖于具体的禁止转速区间推导过程。

2.2   感应发电机效应等效电阻变化规律

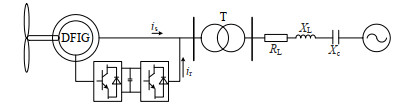
当研究次同步谐振时，可用如图 2所示的单机模型等值整个风电场。图中，T表示升压变压器；i_s表示定子输出电流；i_r表示转子经变流器输出电流；R_L为双馈风力发电场线路电阻；X_L、X_C分别为双馈风力发电场线路电抗、串补电容容抗。在标幺值系统下，转速与频率的标幺值相等，在本文以下分析中不进行区分，统一用频率标幺值表示。

图  2  双馈风电场串补系统等值电路

Figure  2.  Equivalent circuit of the doubly-fed wind farm connected to a series-compensated system

下载: 全尺寸图片 幻灯片

由于输电线路包含串补电容，双馈风机的定子回路存在一个自然谐振频率(也称次同步谐振频率)：

式中：f₀为系统同步频率；X_LΣ为从等值双馈风机后向系统看进去的同步频率等值电抗。X_C/X_LΣ为线路串补度，即系统容抗和感抗之比。

当系统受到扰动后，定子回路会产生次同步频率f_sr的电压$\Delta {\dot U_1}({f_{{\text{sr}}}})$和电流$\Delta {\dot I_1}({f_{{\text{sr}}}})$，从定子侧向转子回路看进去的转子回路等效电阻${R'_{{\text{req}}}}({f_{\text{r}}}, {f_{{\text{sr}}}})$如式(7)所示，双馈风机转子回路与激磁回路并联等值电阻(以下称为转子并联等效电阻)R_req(f_r, f_sr)如式(8)所示。

式中：f_r为转子转速；R_r为双馈风机转子电阻；R_RSC为转子侧变流器在自然谐振频率下的等值电阻；X_r、X_m分别为双馈风机转子漏抗、励磁电抗。

从系统侧向双馈风机看进去的等值电阻R_total(f_r, f_sr)为

其中，输电线路电阻R_L(f_r, f_sr)和双馈风机定子回路电阻R_S(f_r, f_sr)均为正值。

根据文献[17]，双馈风电场发生感应发电机效应产生的条件为从系统侧向双馈风机看进去的等值电阻R_total(f_r, f_sr)为负值。在串补度给定的情况下，系统等值电阻R_total(f_r, f_sr)是风机转速f_r的函数，2.3节将分析风机转速对于系统等值电阻的影响R_total(f_r, f_sr)。

2.3   感应发电机效应危险区域分析

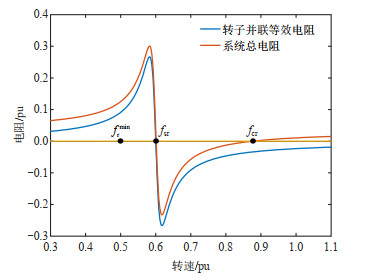
线路串补度给定后，可以基于式(8)和(9)绘制转子并联等效电阻R_req(f_r, f_sr)和系统等值电阻R_total(f_r, f_sr)关于风机转速的函数曲线。图 3展示了线路串补度为36%，f_sr=0.6 pu的情况下，转子并联等效电阻和系统总等值电阻随转子转速的变化曲线。求解方程R_total(f_r, f_sr)=0(可利用MATLAB的solve函数)，在系统谐振频率f_sr的右侧存在2个根(转速点)，假设靠近f_sr的转速点为f′_sr，远离f_sr的转速点为临界转速f_cr。f′_sr、f_sr取值极为接近，这是由R_req和R_total的表达式决定的(图 3中的R_total曲线可以通过将R_req曲线沿y轴正方向移动R₁距离得到，由于R_req曲线在f_sr附近的斜率很大，因此R_total=0的根f′_sr会十分靠近R_req=0的根f_sr)。基于文献[17]的参数设置以及36%的串补度，可计算得到f′_sr和f_sr取值分别为0.601 1和0.6，相对偏差仅为0.18%。出于简化的目的，本文直接采用f_sr代替f′_sr，因此f′_sr在图 3中并未标注，仅标注了远离f_sr的f_cr。在f_sr≤f_r≤f_cr范围内，系统总等值电阻为负值，系统面临次同步谐振的危险，转速区间[f_sr, f_cr]即为风电场的禁止转速区间。

图  3  系统等值电阻随转速的变化曲线

Figure  3.  Variation curves of the equivalent resistance with rotor speed

下载: 全尺寸图片 幻灯片

在设置风机运行点时，应尽量避开上述“禁止转速区间”以保证系统安全。风机的转速一方面受到风速影响，另一方面直接影响风电场的出力功率，进而影响风电场的备用。下文将分析在不同的风速下，风机呈现的3种不同运行工况及在这3种工况下，禁止转速区间对风电出力和备用的影响。

2.4   禁止转速区间对风电备用的影响

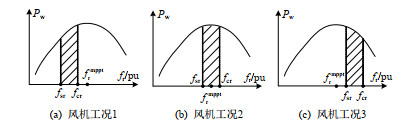
根据风速和串补度的不同，风机MPPT转速和禁止转速区间的相对位置可能出现如图 4所示的3种不同的工况。

图  4  MPPT转速和禁止转速区间的相对位置

Figure  4.  Relative position of MPPT rotor speed and prohibited rotor speed zones

下载: 全尺寸图片 幻灯片

工况1：禁止转速区间位于MPPT转速的左侧，即${f_{{\text{cr}}}} \leqslant f_{\text{r}}^{{\text{mppt}}}$，此时禁止转速区间对风电场运行并不会产生影响，转速调节范围为$[f_{\text{r}}^{{\text{mppt}}}, f_{\text{r}}^{\max }]$，日前和日内风机转速需满足：

工况2：MPPT转速位于禁止转速区间内，即${f_{{\text{sr}}}} \leqslant f_{\text{r}}^{{\text{mppt}}} \lt {f_{{\text{cr}}}}$，此时风机转速调节范围为$[f_{{\text{cr}}}^{},$ $f_{\text{r}}^{\max }]$，日前和日内风机转速需满足：

工况3：禁止转速区间位于MPPT转速右侧，即$f_{\text{r}}^{{\text{mppt}}} \lt {f_{{\text{sr}}}}$，此时风机转速调节范围为$[f_{\text{r}}^{{\text{mppt}}},$ $f_{{\text{sr}}}^{}]$，日前和日内风机转速需满足：

关于所提模型，有如下2点需补充说明。

1）由于本文采用随机场景刻画风速不确定性，当风速场景给定后，风机运行于1、2、3何种工况随之确定，因此无须额外引入0-1变量以表征风机处于何种运行工况。但需要注意的是，如果采用鲁棒优化等其他不确定性优化建模框架来刻画风速不确定性，情况可能会变得更加复杂。以鲁棒优化为例，当日内不确定性风速采用不确定性变量$V_{w, t}^{\text{u}}$表示，并在给定上下界范围内随机取值，这会从两方面增加模型求解的难度：1）由于日内风电功率表达式为${P_w} = {\text{π }}\rho {r^2}{C_p}V_w^3/2$，日内风速转化为不确定性变量会导致模型中出现${C_p}V_w^3$这一非线性项；2）MPPT转速变为不确定性变量，风机的运行工况同样具有不确定性(因为风机的运行工况取决于禁止转速区间和MPPT转速的相对位置)，需要引入0-1变量来指示风机运行工况，而0-1变量会极大增加问题复杂度，需要通过嵌套式C & CG等优化方法进行求解。作者后续会对此进行深入研究。

2）将f_sr和f_cr均设置为小于MPPT转速的值(比如0)，所提模型即可退化为不考虑禁止转速区间的备用优化模型。

2.5   计及禁止转速区间的风电备用模型

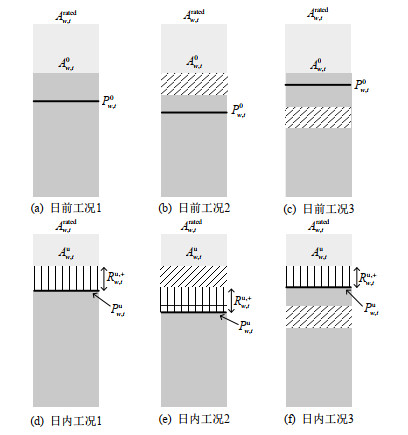
考虑禁止转速区间后，风电备用模型可利用图 5描述，图中黑色横线为风电并网功率，斜线阴影区域为禁止转速区间对应的风电功率(下文简称为禁止风电功率)，网格线阴影区域为日内风电留取的一次调频备用功率。

图  5  计及禁止转速区间的风电备用模型

Figure  5.  Reserve model of wind power considering prohibited rotor speed zone

下载: 全尺寸图片 幻灯片

图 5(a)—(c)展示的是日前阶段风机在不同工况下的并网功率调节范围。当运行在工况1，风机并网功率可在0至MPPT功率之间调节；当运行在工况2，风机并网功率可在0至禁止风电功率下界之间调节；当运行在工况3，风机并网功率可在禁止风电功率上界至MPPT功率之间调节。图 5(d)—(f)为日内阶段风机在不同工况下的并网功率调节范围以及PFR。当运行在工况1，风电并网功率和PFR可在0至MPPT功率之间调节；当运行在工况2，风电并网功率和PFR可在0至禁止风电功率下界之间调节；当运行在工况3，风电并网功率和PFR可在禁止风电功率上界至MPPT功率之间调节。

2.6   弃风功率定义修正

传统优化模型中，弃风通常定义为最大可用风电功率(即MPPT功率)和实际并网风电功率的差值^[21]。但对于图 4工况2，若仍采用该定义，则相当于惩罚风电场为避免系统发生次同步谐振而做出的运行方式调整，不合情理。因此本文将工况2弃风的定义调整为f_cr转速对应的风电功率和实际并网风电功率的差值。

3.   计及决策依赖不确定性和禁止转速区间的频率约束风火协同备用优化模型

3.1   目标函数

目标函数由日前成本和日内成本两部分构成，其中日前包括火电机组启停成本、燃料成本以及备用成本，日内包括火电和风电一次调频备用成本以及弃风弃负荷惩罚。

式中：u_{g, t}和v_{g, t}为火电机组启停动作指示符，取值为1表示机组执行开机或停机动作；$P_{g, t}^0$为日前火电机组出力；$R_{g, t}^ +$和$R_{g, t}^ -$为火电机组上备用和下备用功率；ρ_s为场景s对应的概率；$R_{g, t, s}^{{\text{u, F}}}$和$R_{w, t, s}^{{\text{u}}, {\text{F}}}$为日内火电和风电频率备用；$P_{w, t, s}^{{\text{u, curt}}}$和$P_{d, t, s}^{{\text{u, shed}}}$为日内弃风和弃负荷功率；g、w、d、t、s分别为火电机组、风电场、负荷节点、调度时段以及风速场景的索引；G、W、D、T和S分别为火电机组、风电场、负荷节点、调度时段以及风速场景的集合。变量上标“0”表示日前阶段变量，上标“u”表示日内阶段变量，下同。

3.2   日前阶段约束条件

日前阶段约束条件包括火电机组启停动作和启停状态的耦合约束式(14)、同步发电机出力及备用约束式(15)、同步发电机爬坡约束式(16)、风电场出力约束式(17)、转速约束式(18)、功率平衡约束式(19)以及线路潮流约束式(20)。最小开停机时间约束可见文献[21]，限于篇幅此处不再赘述。对于处于工况1、2、3的风机，转速需要分别满足约束式(10)—(12)。

式中：i_{g, t}为表示机组启停状态的指示符(取1表示机组处于开机状态，取0表示处于停机状态)；$P_g^{\max }$和$P_g^{\min }$为火电机组最大和最小技术出力；$r_g^ +$和$r_g^ -$为火电机组的上下爬坡速率限值；P_{d, t}为负荷功率；S_lg、S_lw和S_ld为火电机组g、风电场w和负荷d对线路l的功率转移分布因子；${\bar F_l}$为线路l的载流上限。

3.3   日内阶段约束条件

3.3.1   常规运行约束

日内常规运行约束包括火电机组出力调整约束式(21)，N−1备用约束式(22)、风电场日内出力以及频率备用功率约束式(23)—(25)。对于工况1、2、3，日内转速以及转速调节裕度约束需要分别满足约束式(26)—(28)。功率平衡约束以及线路潮流约束形式同日前阶段，此处不再赘述。

3.3.2   频率稳定约束

瞬时功率扰动后的系统频率动态过程可用式(29)所示的摇摆方程加以描述。由于频率稳定约束对日内各场景均存在，为表达方便，下文推导略去场景索引。

式中：$H_t^G$和$H_t^W$为火电机组和风电场惯量，如式(30)所示，其中$H_g^G$为火电机组惯量常数，为风电场虚拟惯量常数，体现了风机虚拟惯量控制的作用；$\Delta f(\tau )$为频率偏移量；$D$为负荷阻尼系数；$P_t^D$为系统负荷功率；ΔP_{g, t}(τ)和ΔP_{w, t}(τ)为功率扰动后的火电机组增发的一次调频功率以及风电场通过下垂控制增发的一次调频功率，参考文献[15]，假设其满足式(31)、(32)，式中t_DB为频率偏差达到下垂控制死区Δf_DB的时间，T_d为一次调频响应时间。

频率稳定约束包括频率变化率(rate of change of frequency，RoCoF)约束、频率最低点约束以及稳态频差约束，推导如下：

1）RoCoF约束。最大的RoCoF出现在扰动功率发生的瞬时(即τ =0)，由式(29)可推导出RoCoF约束：

2）频率最低点约束。文献[8]已证明频率最低点约束成立的充分条件为式(34)成立。其中，R_t为系统一次调频备用总量；κ_t为式(35)的解；${D'_t} =$ $DP_t^D$；$\Delta {f^{\max }}$为最大允许频差。

代入式(33)中$H_t^G$和$H_t^W$的表达式，式(34)可转化为式(36)，借助大M法可转化为式(37)。

式中：M为一足够大的正数；X_{g, t}为辅助变量。

3）稳态频差约束。频率达到稳态后有式(38)成立，将其代入式(29)可推出稳态频差约束式(39)，式中$\Delta f_{{\text{qss}}}^{\max }$为允许的最大稳态频差。

4.   求解方法

所建立的求解模型中包含C_p这一非线性项，虽然可以通过分段线性化和大M法将模型转化为混合整数线性规划(mixed integer linear programming，MILP)模型，但这会在第二阶段问题中引入大量0-1变量，严重降低求解效率。为解决这一问题，本文采取如下求解策略。

1）根据风机的禁止转速区间、最大转速以及MPPT转速，结合图 4，计算得到风能捕获系数C_p的取值范围。对于工况1，C_p取值范围为$[C_p^{f_{\text{r}}^{\max }},$ $C_p^{f_{\text{r}}^{{\text{mppt}}}}]$；对于工况2，C_p取值范围为$[C_p^{f_{\text{r}}^{\max }}, C_p^{f_{{\text{cr}}}^{}}]$；对于工况3，C_p取值范围为$[C_p^{f_{{\text{sr}}}^{}}, C_p^{f_{\text{r}}^{{\text{mppt}}}}]$。

2）以C_p为决策变量进行求解，得到C_p的求解结果；

3）根据式(1)计算出对应的转速。

上述处理方式在避免对C_p进行复杂的线性化操作的前提下，将原问题转化为MILP问题，从而可利用gurobi等商业求解器求解。

5.   算例分析

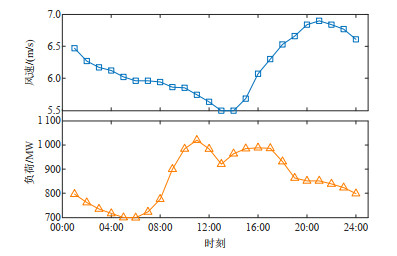
采用文献[17]中相关参数以及36%的串补度可求得禁止转速区间为[0.6, 0.876]。日前预测风速数据来源于美国国家可再生能源实验室，负荷数据基于我国某省实际负荷调整得到，如图 6所示。日内风速随机场景在预测风速曲线的基础上按照正态分布(均值取预测风速，标准差取预测风速的10%)采样获得，场景数目取10。最大频率偏差、频率变化率以及稳态频差限值分别取0.8 Hz、0.25 Hz/s以及0.2 Hz，一次调频死区取0.015 Hz，负荷阻尼系数取0.01，一次调频备用响应时间取10 s。测试环境为Intel-i7-CPU@2.60 GHz、32 GB RAM、MATLAB R2022a/Yalmip、GUROBI 10.0。

图  6  预测风速及负荷曲线

Figure  6.  Curves of predicted wind speed and load

下载: 全尺寸图片 幻灯片

需要说明的是，由于实际风速与风机额定风速可能存在较大差别，实际最大可用风电功率与风电装机容量之间同样可能存在较大差别，因此本文根据日内风速最大值对应的风电功率$P_W^{{\text{u}}, \max }$和火电装机容量$P_G^{\max }$来计算风电渗透率${r_{\text{p}}}$，即${r_{\text{p}}} = P_W^{{\text{u}}, \max }/$ $(P_W^{{\text{u}}, \max } + P_G^{\max })$。

本文采用如下4种备用优化方案进行对比分析。方案1：不考虑频率安全约束，不考虑禁止转速区间，风机采用MPPT控制；方案2：考虑频率安全约束，不考虑禁止转速区间，风机采用MPPT控制；方案3：考虑频率安全约束，不考虑禁止转速区间，风机通过超速控制提供备用；方案4：考虑频率安全约束，考虑禁止区间，风机通过超速控制提供备用。

5.1   9节点系统

首先采用9节点系统进行算例分析。该系统包含3台传统火电机组和一座风电场，火电机组最大技术出力分别为340.2、408.2、367.4 MW，总装机容量为1 115.8 MW；风电场日内最大可用功率为724.9 MW，风电渗透率为39.38%。最大负荷功率为1 020.2 MW。火电机组最小技术出力取最大技术出力的40%，上下爬坡速率取最大技术出力的25%，最小开停机时间分别为4、5、4 h。火电日前上下备用成本分别为5、5.5、6美元/MW，风电日前上下备用成本为3美元/MW，火电日内频率备用成本为15、16.5、18美元/MW，风电日内频率备用成本为8美元/MW。

4种方案的系统运行总成本如表 1所示。总成本排序：方案2 > 方案4 > 方案1 > 方案3。由于方案1和2风机均采用MPPT控制，当日内风速较高时，系统会出现较多的强迫弃风，同时由于方案2风机不参与提供PFR，全部PFR均由火电机组承担，因此PFR成本为所有方案中最高。方案3和4均考虑风机通过超速控制提供PFR，因此PFR成本和弃风功率均低于方案2。对比方案3和4，由于方案4考虑了风机禁止转速区间，风机调频能力受限，PFR成本从方案3的18 556美元降至6 949美元，同时，日内也出现了一定量的弃风。而方案1由于不考虑频率稳定约束，因此火电和风电均未提供PFR，通过后文算例可以看出，方案1无法保证系统在功率扰动下的频率稳定性。

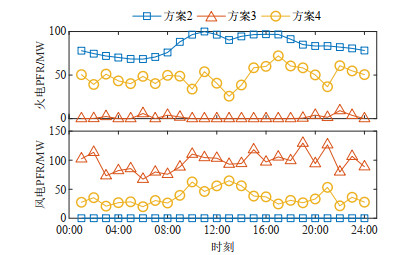
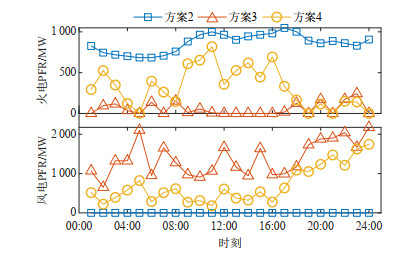
表  1  4种方案运行成本

Table  1.  Operation cost of four schemes 单位: 美元

成本	总成本	启停成本	燃料成本	日前火电上备用成本	日前火电下备用成本	日内火电PFR成本	日内风电PFR成本	日内弃风惩罚
方案1	212 517	7 000	133 048	17 453	13 576	0	0	41 440
方案2	254 166	7 000	133 868	27 893	13 678	30 287	0	41 440
方案3	187 491	7 000	133 227	28186	0	522	18 556	0
方案4	214 053	7 000	133 543	29 364	9 507	17 643	6 949	10 105

下载: 导出CSV 

| 显示表格

图 7展示了方案2—4的火电和风电一次调频备用。由于方案2不考虑风机通过超速控制提供PFR，全部PFR均由火电机组承担，故其火电PFR最高，PFR总成本为全部方案中最高。方案3和4均考虑风电提供PFR，因此火电PFR均低于方案2。但由于方案4考虑了风机禁止转速区间，其风电提供PFR的能力受到限制，风电PFR水平低于方案3，为满足频率稳定要求，其火电PFR高于方案3。

图  7  火电和风电频率备用

Figure  7.  PFR from thermal power and wind power

下载: 全尺寸图片 幻灯片

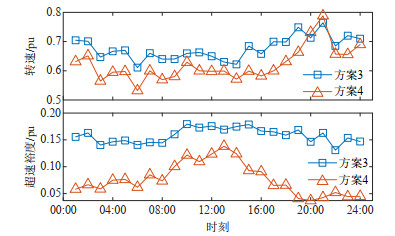
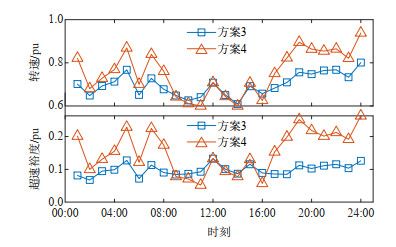
图 8展示了方案3和4的日内各场景转速和超速裕度均值。由于方案3未考虑转速禁止区间，因此具有更大的超速裕度以及频率备用空间，除时段20—21，其转速均值均高于方案4。而由于时段20—21风速较高，方案4风机在部分日内场景下运行于工况2，风机转速下限抬高，备用能力受限，为提供足够一次调频备用以满足频率稳定要求，风机需进一步提高转速以保证足够的超速裕度，因此方案4转速高于方案3。受禁止转速区间影响，方案4各时段超速裕度均低于方案3。其中，低风速时段的MPPT转速更低，超速裕度受影响更小。

图  8  转速和超速裕度

Figure  8.  Rotor speed and overspeed margin

下载: 全尺寸图片 幻灯片

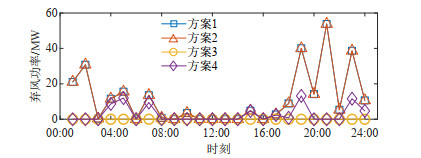
图 9展示了4种方案的日内弃风功率。由于方案1和2无法通过超速控制将无法消纳的部分风功率转化为PFR，因此在高风速时段存在一定弃风。方案4受到禁止区间影响，当风机运行于工况3，转速受到禁止转速区间下界的限制，无法进一步超速减载，仍会出现无法避免的弃风。对比之下，由于方案3不考虑禁止转速区间，日内弃风最小。

图  9  各方案日内弃风

Figure  9.  Intra-day wind curtailment of four schemes

下载: 全尺寸图片 幻灯片

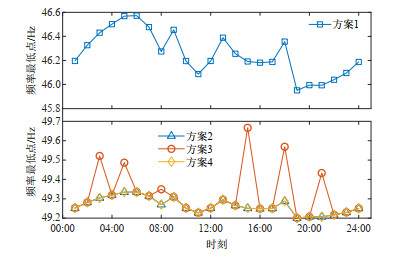
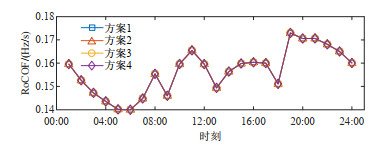
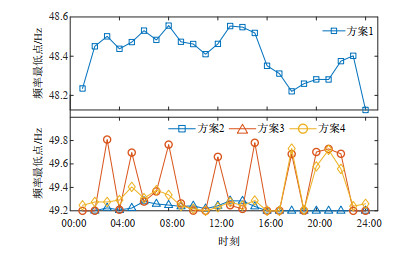
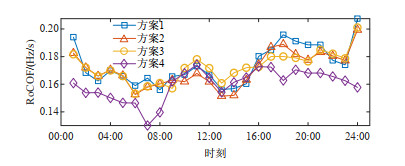
图 10和11展示了4种方案各时刻受扰动后的频率最低点和最大频率变化率。对于方案1，由于其未添加频率稳定约束，因此火电机组和风电机组均未留取一次调频备用，其频率最低点亦远低于稳定约束限值。而方案2—4由于添加了频率安全约束，其各时段频率最低点均在限值49.2 Hz之上。其中方案3部分时段的频率最低点更高，这是因为在部分高风速时段，方案3将部分无法并网消纳的风功率作为一次调频备用，系统一次调频总备用高于方案2和4，频率最低点更高。而由于4种方案具有相同的机组组合，因此各方案的最大频率变化率，并都在限值0.25 Hz/s以下。

图  10  各方案频率最低点

Figure  10.  Frequency nadir of four schemes

下载: 全尺寸图片 幻灯片

图  11  各方案最大频率变化率

Figure  11.  Maximum RoCoF of four schemes

下载: 全尺寸图片 幻灯片

5.2   118节点系统

进一步采用118节点系统进行算例分析。该系统包含54台传统火电机组、186条线路，节点4、21和28各接有一座风电场。火电机组的装机容量为13 562 MW，风电场最大风电出力为11 546 MW，风电渗透率为45.98%，最大负荷为10 202 MW。

4种方案的系统运行总成本如表 2所示。总成本排序：方案2 > 方案1 > 方案4 > 方案3。方案3和4通过风机提供频率备用减少了频率备用总成本以及日内弃风，因此具有比方案1和2更低的总成本。考虑禁止转速区间后，方案4的风电频率备用受限，系统一次调频备用总成本和运行总成本相较于方案3均上升。

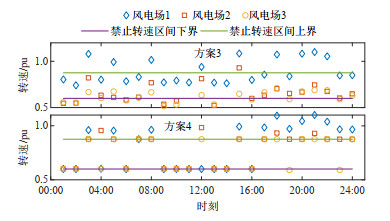
表  2  4种方案运行成本

Table  2.  Operation cost of four schemes 单位: 美元

成本	总成本	启停成本	燃料成本	日前火电上备用成本	日前火电下备用成本	日内火电PFR成本	日内风电PFR成本	日内弃风惩罚	日内弃负荷惩罚
方案1	3 998 183	67 000	698 646	196 947	30 305	0	0	2 971 124	34 161
方案2	4 510 139	81 000	716 209	302 820	28 850	317 532	0	3 063 729	0
方案3	1 269 583	50 000	713 937	282 592	0	21 096	201 958	0	0
方案4	1 642 505	54 000	1 005 708	228 670	42 334	117 386	110 857	83 549	0

下载: 导出CSV 

| 显示表格

图 12展示了方案2~4的火电和风电一次调频备用。火电PFR满足方案2 > 方案4 > 方案3，风电PFR满足方案3 > 方案4 > 方案2。图 13展示了方案3和4的日内各场景转速和超速裕度均值。方案4受禁止转速区间影响，超速裕度低于方案3。图 14以风速场景1为例，展示了方案3和4各风电场的日内转速。其中，方案3风电场转速较多地分布在禁止转速区间内，而方案4的风电场转速则避开了禁止转速区间，其中：分布于禁止转速区间上界及以上的运行点对应工况2，分布于禁止转速区间下界的运行点对应工况3，对于工况3，在禁止转速区间影响下，风机的备用能力受到限制，为最大程度提供PFR，运行点位于转速区间下界。

图  12  火电和风电一次调频备用

Figure  12.  PFR from thermal power and wind power

下载: 全尺寸图片 幻灯片

图  13  转速和超速裕度

Figure  13.  Rotor speed and overspeed margin

下载: 全尺寸图片 幻灯片

图  14  方案3和方案4在场景1中的风电场转速

Figure  14.  Rotor speed of scheme 3 and 4 under wind speed scenario 1

下载: 全尺寸图片 幻灯片

图 15和16展示了4种方案各时刻受扰动后的频率最低点和最大频率变化率。方案1，由于未添加频率稳定约束，其频率最低点亦远低于稳定约束限值。而方案2~4由于添加了频率安全约束，其各时段频率最低点均在限值49.2 Hz之上。其中方案3部分时段的频率最低点更高，这是因为在部分高风速时段，方案3将部分无法并网消纳的风功率作为一次调频备用，系统一次调频总备用高于方案2和4，频率最低点更高。4种方案的机组组合有所差异，因此，最大频率变化率有所不同，但均在限值0.25 Hz/s以下。

图  15  各方案频率最低点

Figure  15.  Frequency nadir of four schemes

下载: 全尺寸图片 幻灯片

图  16  各方案最大频率变化率

Figure  16.  Maximum RoCoF of four schemes

下载: 全尺寸图片 幻灯片

算例总求解时间为1 049 s，约17.48 min，可以满足日前调度的需求；而采用分段线性化和大M法，在1 h内无法得到最优解，这表明本文算法是高效的。

6.   结论

风电场为系统提供频率支撑，协同参与系统备用是未来新型电力系统灵活高效运行的关键问题。本文在风电通过超速控制提供一次调频备用的基础上，考虑风电备用的决策依赖不确定性，以及禁止转速区间对风电备用的影响，建立了风火协同两阶段随机备用优化模型，通过算例分析得出如下结论：

1）在模型中考虑频率安全约束虽然会增加系统运行成本，但可保证系统在功率扰动下的频率稳定；

2）风机参与提供一次调频备用，可有效降低传统火电机组的备用压力以及系统整体运行成本；

3）在模型中考虑风机禁止转速区间虽然会限制风电场的一次调频能力，但有助于系统避开次同步谐振危险运行点，更利于系统安全稳定运行；

4）后续研究可以进一步考虑风电和其他灵活资源的协同，以进一步提升系统运行的经济性和可靠性。基于鲁棒优化等不确定性优化框架对当前模型进行拓展同样值得深入研究。