Online Identification of Key Parameters of Secondary Edges in Underwater WPT System Based on Unscented Kalman Filtering Algorithm
-
摘要: 为提升无线电能传输(wireless power transfer,WPT)系统传输性能,需在控制过程中实时获取负载与耦合系数等关键信息,而该信息的获取目前普遍采用无线通讯模块或增加额外通信线圈等方式,增加了系统复杂度,尤其面临复杂水下工况及高频电磁环境,在通讯过程中极易造成通讯异常而导致系统瘫痪。为此,文中提出一种新型基于无迹卡尔曼滤波的WPT系统互感及负载关键参数在线识别方法,该方法仅需采样原边侧电压瞬时值,即可实时获取互感与负载等关键参数信息。同时为提升辨识精度与收敛速度,采用离线式神经网络指导粒子群优化算法建立系统噪声协方差矩阵。实验结果表明,该算法具有模型简单、计算精度较高等特点,在变负载、变移相控制角及偏移情况下,所提出的在线辨识方法对负载与互感的最大识别误差分别为6.19%和1.7%,且2 ms左右即可完成负载的动态识别,具有一定的工程应用价值。Abstract: In order to improve the transmission performance of wireless power transfer (WPT) system, it is necessary to obtain key information such as load and coupling coefficient in real time during the control process. Currently, acquiring this information typically involves using wireless communication modules or adding additional communication coils, which adds complexity to the system. This complexity is further exacerbated in complex aquatic conditions and high-frequency electromagnetic environments, where abnormal communication during the process is highly likely to cause system paralysis. For this purpose, this paper proposes a novel Unscented Kalman filter (UKF) based online identification method for the critical parameters of the WPT system's transients and loads. This method only samples the instantaneous value of the voltage at the edge of origin, and can acquire the information of critical parameters such as transients and loads in real time. At the same time, to improve the discrimination accuracy and convergence speed, the offline neural network guided particle swarm optimization (PSO-NN) algorithm is used to establish a systematic noise covariance matrix. The experimental results show that the proposed online discrimination method achieves the maximum identification errors of 6.19% and 1.7% for load and mutual inductance, respectively, in the case of varying load, varying phase control angle and offset. The dynamic identification of load can be completed in about 2 ms, which has some engineering applications.
-
0. 引言
无线电能传输(wireless power transfer,WPT)技术克服了传统线缆连接传能的线路冗余、磨损老化、范围受限等缺点,具有方便灵活、安全可靠、智能化程度高、适应极端恶劣天气和环境等优点,因而在电动汽车、机器人、自动水下航行器(autonomous underwater vehicle,AUV)、电子产品、生物医疗、智能家居等领域得到了广泛的关注和应用[1-6]。
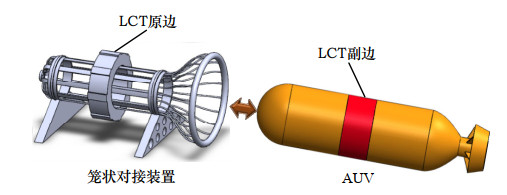
本文设计的笼状对接无线充电系统如图 1所示。当AUV需补充电能时,首先通过导航系统将AUV引入笼状对接装置,同时发出充电信号,水下无线充电系统开始对AUV进行电能补给[7]。由于水下工况复杂,在水下无线充电过程中,极易造成系统能量发射端与接收端相对位置发生偏移,即耦合系数发生改变,同时结合充电过程中电池负载的实时变化,使得系统等效负载在充电过程中变化范围较宽[8],必须施以相应的控制策略以提升系统传输性能[9-11]。显然,无论采取何种控制策略,其重要环节是要获取负载与耦合系数两大关键参数,为此目前普遍采用无线通讯模块或增加额外通信线圈等方式满足WPT系统无线通信需求,但面临复杂工况及高频电磁环境,在通信过程中极易出现传输延时、信号干扰、通信安全和信号损伤等问题,降低了系统的安全性与可靠性。因此,通过在线辨识技术精确获取水下WPT系统耦合系数与负载等关键参数,以实现系统实时控制与状态监测,进而使得水下无线充电设备具有更宽的负载适应性与更强的抗偏移能力,将对水下无线充电系统能量的稳定传输及效率提升具有重要意义。
当前,已有大量学者对WPT系统互感与负载参数识别问题开展相关研究并取得一定的成果[12-23]。文献[12]在系统启动时注入一定能量,通过检测自由振荡过程中电流衰减率的方式完成负载识别,仅适用于充电过程负载固定不变的载体;文献[13]基于最小二乘法提出一种负载辨识策略,等效负载电阻与不控整流桥等效输入阻抗之间的关系使用8/π2建立,而在更加精确的描述下,整流桥等效输入阻抗可以表示为电感与电阻串联的LR电路[20, 24],以上文献将互感作为已知固定不变参数,而只针对负载变化进行识别,其实用性受到一定限制。文献[14-15]分别通过投切电容和辅助逆变器的方式改变系统工作状态,以此实现互感与负载参数识别;文献[16-19]测量逆变器输出电压电流的幅值、相位、有效值等相关信息,依据电路分析法建立互感和负载与测量量之间的数学关系进行求解;文献[20-21]利用逆变器产生的谐波建立传输模型实现对互感和负载的估计;文献[22]将负载与互感识别问题转化为参数值优化问题,从而基于遗传算法对待识别参数最优解进行搜索;文献[23]提出一种接收侧多参数联合辨识的方法,仅需一个电压量即可实现电池电压、等效负载电阻、充电电流、整流桥等效输入阻抗等多个参数的联合辨识。上述方法在取消无线通信进而提升可靠性方面取得了丰硕的成果,但其分别具有如下问题:1)电路和控制复杂造成接收侧体积增大、成本增加、灵活性变差、可靠性低;2)算法复杂、数据存储量及运算量巨大,对寄存器和数据处理器要求较高;3)多适用于稳态识别工况,存在采样数据处理量大及计算耗时长等问题,在实际工程中的应用价值不高。
针对上述问题,本文提出一种基于无迹卡尔曼滤波(unscented Kalman filtering,UKF)的WPT系统互感与负载关键参数在线辨识算法,该算法具有模型简单、运算量较小、计算精度较高等特点,已广泛应用于同步电机系统状态参数估计[25-29]等领域,而应用于WPT系统领域研究相对较少。鉴于UKF算法的诸多优点,本文首先基于阻感性不控整流等效输入阻抗对WPT系统进行建模,通过反映阻抗法将接收端信息折算至发射端,由简化等效电路获得系统状态方程;后引入UKF算法,并通过离线式神经网络指导粒子群优化(neural network guided particle swarm optimization,PSO-NN)方式获取关键参数系统噪声协方差矩阵Q,进而实现对互感与负载参数的在线估计;最后搭建一套WPT样机对所提方法进行实验验证。
1. WPT系统数学模型
1.1 系统概述
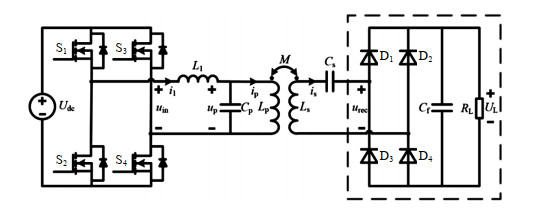
考虑到LCL-S拓扑结构具有发射线圈恒流、接收侧与负载解耦的恒压输出特性,因此本文基于二极管全桥不控整流与LCL-S补偿拓扑WPT系统进行研究,具体电路拓扑如图 2所示,其中:Udc为直流输入电源;开关管S1—S4构成H全桥逆变电路;L1为原边谐振补偿电感;Cp、Cs分别为原副边谐振补偿电容;Lp、Ls和M分别为发射线圈和接收线圈自感及两者之间的互感;D1—D4为副边不控整流二极管;Cf为滤波电容;RL为负载;uin和i1分别为逆变器输出的方波电压和电流;up和ip分别为发射线圈两端电压和电流;urec和is分别为不控整流输入电压与输入电流;UL为负载电压。
1.2 等效电路模型
为更加精确地估计负载参数信息,本文基于文献[20, 24]中提出的不控整流等效输入阻抗计算方法,对LCL-S补偿结构WPT系统不控整流等效输入阻抗进行计算,得到不控整流输入侧电压和电流的基波幅值及相位:
{|Au|=Usθu=0|Ai|=Us√4R2L+π4ω2L2s8ωLsRLθi=arctan(−2RLπ2ωLs) (1) 根据阻抗Zb = | Au | ejθ u/(| Ai | ejθ i),最后可得出不控整流输入侧等效阻抗的实部与虚部表达式:
{Rb=8π2ω2L2sRL4R2L+π4ω2L2sLb=16LsR2L4R2L+π4ω2L2s (2) 为便于系统分析,将副边折算至原边,得到引入阻抗Zeq:
Zeq=Req+1jωCeq (3) 其中,Req与Ceq分别为
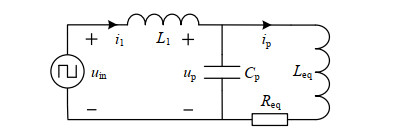
{Req=Rbω2M2R2b+ω2L2bCeq=R2b+ω2L2bLbω4M2 (4) 考虑到系统阶数过高,故将发射线圈自感Lp与引入阻抗中的等效电容Ceq相结合,得到如图 3所示的原边等效电路。其中:
Leq=Lp−1ω2Ceq (5) 根据原边等效电路,系统状态方程可表示为
{di1dt=−1L1up+1L1uindupdt=i1−ipCpdipdt=up−ipReqLeq (6) 式中:L1、Cp和uin为已知量;i1、up和ip可作为状态量及测量量;Leq、Req为未知参数,因而可将其视为系统常值参数识别或时变参数识别的问题进行处理。同时结合实际工程中的相关应用,考虑算法的成熟性、复杂性及可行性,引入卡尔曼滤波相关算法。
2. 基于UKF的互感与负载识别
WPT系统是非线性高阶复杂系统,如采用常规卡尔曼滤波(Kalman filter,KF)算法极易导致系统状态估计精度变差与滤波发散等问题。为此,一般方法是使用扩展卡尔曼滤波(extended Kalman filtering,EKF)算法对系统线性化,其关键在于状态方程与观测方程的一阶泰勒展开,该过程增加计算量的同时降低了精度。因此,本文采用无迹卡尔曼滤波(unscented Kalman filtering,UKF)算法,通过无迹变换的方式代替线性化过程,并建立相应的加权策略。整个过程不需要求导,也没有忽略高阶项,故而计算精度较高。
2.1 WPT系统参数识别模型
为使用UKF算法进行系统参数识别,本文采用增广型无迹卡尔曼滤波器,将WPT系统原边等效电路参数Leq与Req纳入状态量。由于互感与负载相对于系统工作频率和传感器采样频率变化缓慢及考虑到LCL-S补偿拓扑发射线圈恒流特性[30],基于式(6)建立系统状态空间模型:
{˙x=Ax+Bu+wy=Hx+v (7) 式中:w为系统噪声,由系统建模不精确、电子元器件参数漂移以及实验环境噪声等其他因素引起,其协方差为Q;v为观测噪声,由系统传感器的误差造成,协方差为R;同时假设w、v为不相关零均值高斯白噪声。
此外,式(7)中的状态量为x = [i1 up dup/dt Leq Req]T,观测量y = [up],输入量u = uin及状态矩阵A、输入矩阵B和观测矩阵H分别为:
A=[0−1L100000100ReqLeqCp−(1L1Cp+1LeqCp)−ReqLeq000000000000] (8) B=[−1L101L1Cp00] (9) H=[01000] (10) 当采样周期足够小时,可以用式(11)近似的表示式(7)的离散形式,其中A' = I + AT,B' = BT,T为采样周期。
{xk+1=f(xk,uk)+w=A′xk+B′uk+wyk=h(xk,uk)+v=Hxk+v (11) 2.2 UKF算法过程
对于如式(11)所示离散非线性随机系统的状态空间模型,UKF的具体算法过程如下:
1) 初始化状态x和状态误差协方差矩阵P,并设定过程噪声协方差矩阵Q与观测噪声协方差矩阵R。
{ˆx0=E[x0]P0=E[(x0−ˆx0)(x0−ˆx0)T] (12) 2) 在每一个采样周期内(k = 1, 2, ⋅⋅⋅, ∞)通过无迹变换计算Sigma点:
{χ0,k−1=ˆxk−1,i=0χi,k−1=ˆxk−1+(√(n+λ)Pk−1)i,i=1,2,⋯,nχn+i,k−1=ˆxk−1−(√(n+λ)Pk−1)i,i=1,2,⋯,n (13) 式中:(√(n+λ)Pk−1)i为矩阵√(n+λ)Pk−1的第i列;n为状态量x的维数;λ = α 2(n + κ) − n,0 < α < 1表示缩放参数,控制着Sigma点的分布范围,通常取值很小,以避免强非线性系统非局部效应采样的影响;κ ≥ 0,用来减少无迹变换过程中的高阶误差与保证方差阵的半正定,通常在状态估计时取0值,在参数估计时取3 − n。
3) 状态预测。
将上一步中计算得到的Sigma点代入系统状态模型,并采用加权的方式得出系统状态量的先验估计值ˆxk|k−1与先验估计协方差矩阵Pk|k−1:
χi,k|k−1=f(χi,k−1,uk) (14) ˆxk|k−1=2n∑i=0W(m)iχi,k|k−1 (15) Pk|k−1=2n∑i=0W(c)i[(χi,k|k−1−ˆxk|k−1)(χi,k|k−1−ˆxk|k−1)T]+Q (16) 式(15)、(16)中的权值采用式(17)计算,其中β为参数,对于高斯分布通常取β = 2;上标m为均值权重,c为协方差权重。由于权值计算过程中均采用恒定值,因而可使用离线方式计算得到,从而一定程度减小处理器运行过程中的计算量,加快运算速度。
{W(m)0=λn+λ,i=0W(c)0=λn+λ+(1−α2+β),i=0W(m)i=W(c)i=12(n+λ),i=1,2,⋯,2n (17) 4) 观测预测。
将式(14)中计算得到的Sigma点一步预测值χi, k|k−1代入观测函数,同状态预测过程一致,采用加权的方式得到系统观测量的先验估计均值ˉyk与先验估计协方差矩阵Pyk,同时计算出状态量与观测量的互协方差矩阵Pxkyk:
ˆyi,k|k−1=h(χi,k|k−1,uk) (18) ˉyk=2n∑i=0W(m)iˆyi,k|k−1 (19) Pyk=2n∑i=0W(c)i[(ˆyi,k|k−1−ˉyk)(ˆyi,k|k−1−ˉyk)T]+R (20) Pxkyk=2n∑i=0W(c)i(χi,k|k−1−ˆxk|k−1)(ˆyi,k|k−1−ˉyk)T (21) 5) 状态修正。
基于前期的计算准备,以及实际观测量yk的采样输入,同时使用卡尔曼滤波增益Kk对先验估计值ˆxk|k−1进行修正,最终得到k时刻状态量的后验估计值ˆxk及相应的后验估计协方差矩阵Pk。
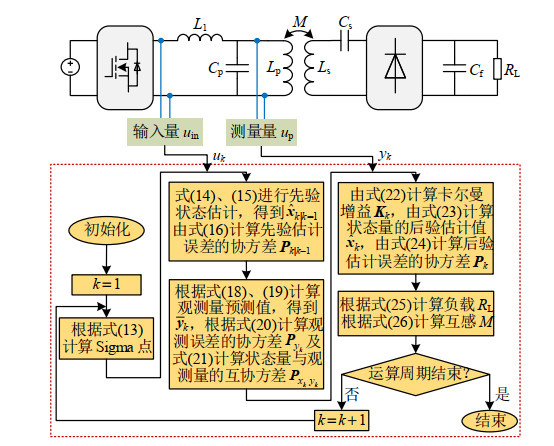
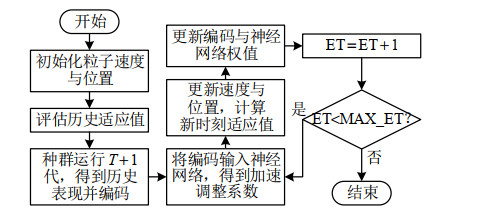
Kk=PxkykP−1yk (22) ˆxk=ˆxk|k−1+Kk(yk−ˉyk) (23) Pk=Pk|k−1−KkPykKTk (24) 根据UKF算法识别出系统等效电路参数Leq与Req后,代入由式(2)—(5)推导得出的式(25)、(26)中,进而计算得到系统负载与互感估计值。至此,基于UKF算法的WPT系统负载与互感参数识别方法完成一个采样周期的计算。随后,循环上述计算过程,完成系统参数的在线识别。图 4为本文参数识别的算法流程图。
RL=ω2π2Ls(Lp−Leq)2Req (25) M=√4Ls(Lp−Leq) (26) 2.3 系统噪声确定
为构建高精度、高稳定性系统关键参数在线辨识方法,首要环节是建立系统噪声协方差矩阵Q,如若该矩阵设计不当,极易造成辨识参数估计精度下降甚至不收敛。鉴于WPT系统具有高阶非线性的特性,本文拟采用离线粒子群优化算法获取协方差Q矩阵,同时为有效平衡搜索过程中的探索和开发,利用神经网络表征粒子自身搜索经验[31]。具体方法如下。
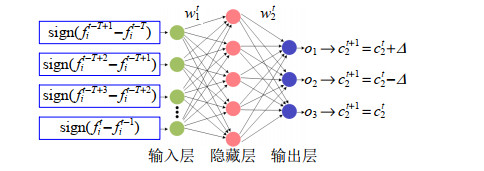
首先,设置种群规模N,并初始化各粒子速度与位置,同时根据目标函数评估适应值;其次,设置神经网络相关参数。本文采用紧凑的三层神经网络,其输入为单个粒子连续T时间序列中历史表现Hit的编码值,公式化表示为
Hti=[sign(ft−T+1i−ft−Ti),⋯,sign(fti−ft−1i)] 式中fit是粒子i在t时刻的适应值(上标t代表当前时刻,t − 1为上一时刻,t + 1为下一时刻),当fit < fit−1,编码为1,反之则编码为−1。隐藏层节点数为2T + 1,其中输入层与隐藏层的激活函数为sigmoid函数,隐藏层与输出层的激活函数为softmax函数,最终输出结果oit为
oti=softmax[wt2⋅sigmoid(Htiwt1)] (27) 式中:w1t为输入层与隐藏层间的权值;w2t为网络隐藏层与输出层间的权值,w1t与w2t可根据梯度下降及反向传播规则实时修正。网络的输出层有3个节点,分别代表单个粒子历史最优学习加速系数c2的3个调整动作,即增强、减弱或不改变开发能力,选取oit的最大值作为c2的调整动作,如最大值为增强开发能力,则在当前c2t的基础上增加一增量Δ,即c2t+1 = c2t + Δ,如最大值为减弱开发能力,则c2t+1 = c2t − Δ。神经网络工作原理如图 5所示。
最后,更新粒子下一时刻的速度vit+1与位置xit+1:
{vt+1i=wvti+ct+11r1(gbest−xti)+ct+12r2(pbesti−xti)xt+1i=xti+vt+1i (28) 式中:c1为种群历史最优学习加速系数,与c2的关系为c = c1 + c2,c为加速系数;w表示惯性权重;r1与r2为均匀分布在(0, 1)间的随机数。图 6为神经网络指导粒子群算法流程,其中MAX_ET为最大评估次数。
针对于本系统,需建立5维搜索空间,对应5阶Q矩阵的对角线元素,第i个粒子表示一个5维向量:
Qi=[qi1,qi2,qi3,qi4,qi5],i=1,2,⋯,N 适应度函数选取为实际测量值yi与估计测量值ˉyi之间的均方根误差,以此结果来反映计算值与实际测量值的接近程度。
min (29) 式中M为数据长度。算法基本参数选取如表 1所示。
表 1 算法基本参数Table 1. Basic parameters of the algorithm参数 数值 参数 数值 N 50 MAX_ET 30 c 4 c2 2 w 0.65 Δ 0.05 3. 实验验证与分析
3.1 实验设计
为验证本文提出的基于无迹卡尔曼滤波算法互感与负载参数识别方法,设计和开发了一套基于LCL-S补偿结构的水下无线电能传输系统实验样机,如图 7所示。实验采用JT6343A型直流电子负载,LW-100010KD型直流电源,RIGOL-DS7024型示波器。此外,为有效避免AUV的径向偏移,本文拟采用圆筒型磁芯结构,同时选用了专用高频谐振MKPH电容,该电容额定频率为50 kHz,具体的实验参数值如表 2所示。
表 2 水下WPT系统参数Table 2. Underwater WPT system parameters参数 数值 参数 数值 直流电压Udc/V 100 原副边线圈互感M/μH 59.4 逆变频率f /kHz 50 原副边线圈匝数/匝 22 激励电感L1/μH 102.2 滤波电容Cf/μF 80 原边补偿电容Cp/nF 99.6 原边线圈电感电阻Rp/mΩ 124 原边线圈电感Lp/μH 101.7 副边线圈电感电阻Rs/mΩ 116 副边线圈电感Ls/μH 98.4 负载电阻RL/Ω 10 副边补偿电容Cs/nF 103 — — 为验证本文所提互感与负载识别算法的准确性与应对不同工况下的识别能力,进行如下实验:首先,在线圈耦合情况不变的条件下,分别改变负载与移相控制角大小,以检测互感与负载的参数识别结果;其次,在两组不同负载大小且各自保持不变的情况下,通过线圈轴向偏移[7]的方式改变耦合情况,再次对本文提出的互感与负载识别方法进行验证和分析;最后,验证UKF算法在不同初始设定值下负载估计的收敛性。
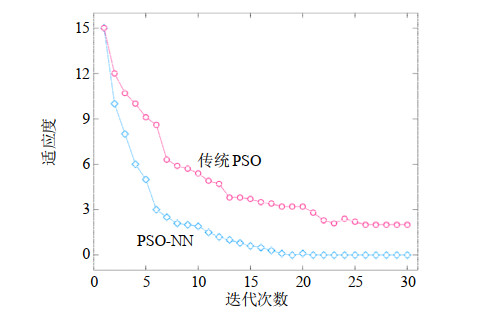
此外,为保证UKF算法的快速收敛,本文基于2.3节所述方法获取系统噪声协方差矩阵Q。图 8给出本文PSO-NN算法与传统PSO算法的适应度变化曲线,由图可知,本文所采用的利用神经网络表征粒子自身搜索经验的方法相比传统PSO优化算法具有更快的收敛速度与更优的适应度。然后,在由此计算出系统噪声协方差矩阵Q值的基础上,通过大量实验验证,并不断对矩阵Q中的元素值进行微调,最终本文实验参数设置如下。其中,观测噪声协方差矩阵R的取值为电压探头的最大测量误差。
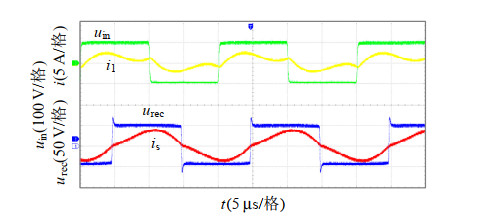
\boldsymbol Q = {\text{diag}}(0.025, 0.1, 1.6 \times {10^{12}}, 5 \times {10^{ - 15}}, 8.6 \times {10^6}) (30) {\boldsymbol P_0} = {\text{diag}}({10^{ - 5}}, {10^{ - 5}}, {10^{ - 5}}, {10^{ - 5}}, {10^{ - 5}}) (31) \boldsymbol R = {\text{diag}}(10) (32) 图 9为逆变器输出电压uin、电流i1与不控整流输入电压urec、电流is的示波器波形图。此时逆变器移相控制角为0°,轴向偏移距离为0。图中电流is明显滞后于电压urec的等效基波,从而验证了将不控整流的输入阻抗等效为阻感形式的必要性。与此同时,逆变器输出电流i1的严重畸变,是i1为非观测量的重要原因。
3.2 不同工况下的实验与分析
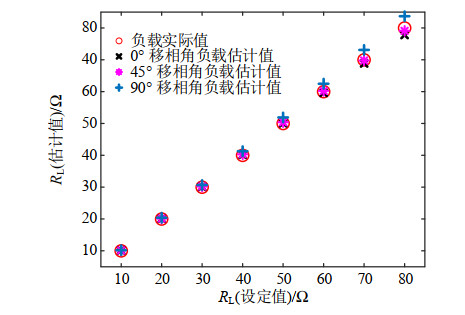
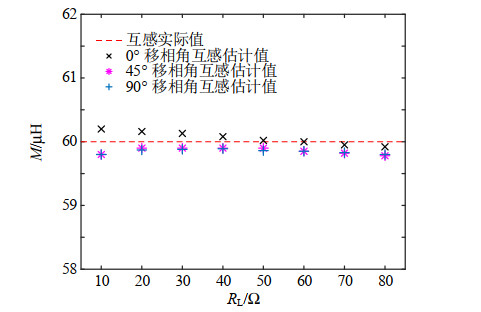
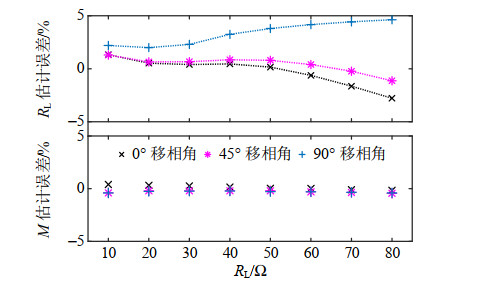
基于设计和开发的实验系统平台,分别在负载变化与线圈轴向偏移的工况下,对本文提出的参数识别方法进行验证与分析。其实验数据通过示波器输出电压uin与up的数组获取,导入Matlab中完成在线识别,图 10—13示出了负载与互感参数在线识别结果。由图 10、11可知,在变负载工况下,随着负载电阻的增加,负载估计结果偏离实际值的程度增大,而互感估计结果影响不大。图 12为变负载工况下负载电阻与互感的估计误差,由图可知,移相角为0°时,10~80 Ω负载范围内最大估计误差为−2.78%,互感估计结果均在2%误差范围内。此外,根据卡尔曼滤波基本工作原理可知,估计误差与系统输入无关,因而本文采用移相控制的方式进行了相关实验。由于移相过程产生的大量高次谐波对系统状态造成一定影响,故而出现图 12中识别误差随移相角的变化。
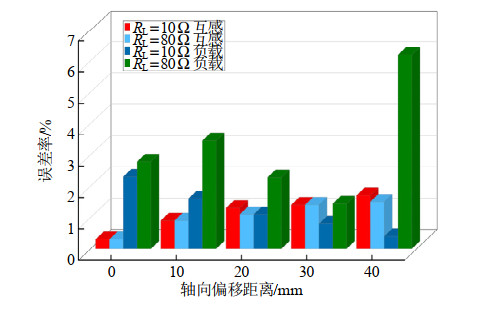
图 13为在不同轴向偏移程度下的参数识别误差结果。由图可知,当偏移距离为4 cm负载80 Ω时,负载识别误差达到最大值6.19%。因此,在轴向偏移的情况下,本文算法对负载与互感识别同样表现出较高的准确性。
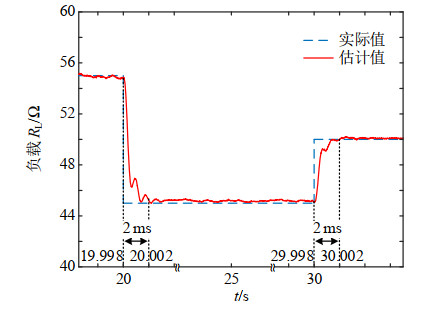
为进一步验证所提参数识别方法的动态性与时效性,实验中通过改变直流电子负载的阻值,使得系统负载发生连续变化,由初始55 Ω变至45 Ω系统稳定后再次改变为50 Ω,实验结果如图 14所示。由实验结果可知,基于UKF算法的负载识别方法基本在2 ms左右的时间即可实现由动态到稳定的准确识别,表现出良好的动态性与时效性,具有极大的实用价值。
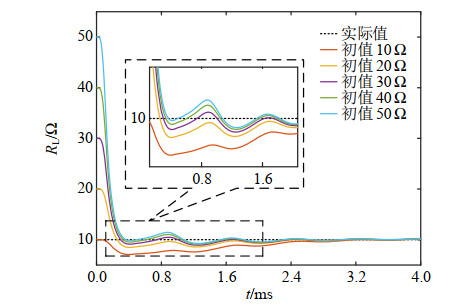
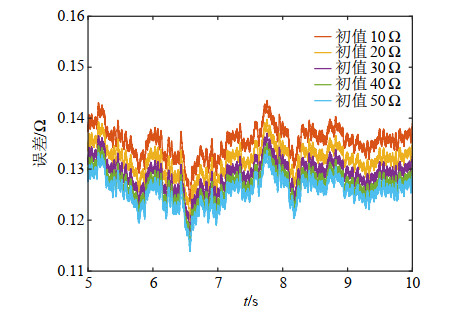
此外,在实际应用中准确获得负载的初始值是极其困难的,因此验证UKF算法在不同错误初始设定值下负载估计的收敛性是十分必要的。本文在实际负载值为10 Ω情况下进行实验,估计负载的初始设定值分别选择10、20、30、40、50 Ω。实验结果如图 15、16所示,图 15为不同初始值下负载估计变化曲线,图 16为5 s后负载估计误差变化曲线。由实验结果可知,在不同初始设定值条件下对WPT系统负载进行参数识别,利用UKF估计算法可以使负载的估计值快速收敛到实际值附近。通过图 15可知,负载估计的收敛速度与初始设定值的误差几乎无关,当初始设定值与实际值之间的误差较大时,经过一段时间的校正(2 ms左右)也能很好的逼近实际值。通过图 16可知,负载的估计误差值与初始状态设定值几乎无关,在初始设定值不同的条件下,稳定后的估计误差值都基本一致(误差不超过1.4%)。
综上所述,本文所提出的基于UKF算法WPT系统互感与负载关键参数在线识别方法具有较高的识别精度、较快的识别速度、以及优越的动态性与时效性,能够实时跟踪识别互感及负载的动态变化;同时还具有模型简单、计算流程简便、对硬件要求比较低等特点,具有很好的实际应用价值。后续研究将着眼于进一步扩大负载及互感的识别范围,提高参数识别的灵活性与极端恶劣条件下的准确性,进而将提出的识别方法应用于WPT系统控制与状态监测。
4. 结论
为解决WPT系统采用常规无线通讯方式导致系统可靠性下降问题,本文提出一种新型基于无迹卡尔曼滤波的WPT系统互感与负载关键参数在线识别方法。该方法仅需采集原边侧电压瞬时值,即可实时获取互感与负载等关键参数信息,最后通过实验验证了该方法的可行性与有效性。得到如下结论:
1) 将UKF算法应用于WPT系统关键参数在线识别,在变负载、变移相控制角及偏移情况下,负载与互感的最大识别误差分别为6.19%和1.7%,且2 ms左右即可完成负载的动态识别,实验结果表明该算法具有模型简单、计算精度较高等特点。
2) 鉴于系统噪声协方差矩阵Q的取值直接关系到参数辨识精度与收敛速度,本文采用了离线式PSO-NN优化算法建立Q矩阵。
3) 该辨识算法同样适用于其他补偿拓扑的WPT系统,具有一定的普适性。
-
表 1 算法基本参数
Table 1 Basic parameters of the algorithm
参数 数值 参数 数值 N 50 MAX_ET 30 c 4 c2 2 w 0.65 Δ 0.05 表 2 水下WPT系统参数
Table 2 Underwater WPT system parameters
参数 数值 参数 数值 直流电压Udc/V 100 原副边线圈互感M/μH 59.4 逆变频率f /kHz 50 原副边线圈匝数/匝 22 激励电感L1/μH 102.2 滤波电容Cf/μF 80 原边补偿电容Cp/nF 99.6 原边线圈电感电阻Rp/mΩ 124 原边线圈电感Lp/μH 101.7 副边线圈电感电阻Rs/mΩ 116 副边线圈电感Ls/μH 98.4 负载电阻RL/Ω 10 副边补偿电容Cs/nF 103 — — -
[1] 赵争鸣, 张艺明, 陈凯楠. 磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程学报, 2013, 33(3): 1-13. http://ntps.epri.sgcc.com.cn/djgcxb/CN/Y2013/V33/I3/2 ZHAO Zhengming, ZHANG Yiming, CHEN Kainan. New progress of magnetically-coupled resonant wireless power transfer technology[J]. Proceedings of the CSEE, 2013, 33(3): 1-13(in Chinese). http://ntps.epri.sgcc.com.cn/djgcxb/CN/Y2013/V33/I3/2
[2] 范兴明, 莫小勇, 张鑫. 无线电能传输技术的研究现状与应用[J]. 中国电机工程学报, 2015, 35(10): 2584-2600. DOI: 10.13334/j.0258-8013.pcsee.2015.10.026 FAN Xingming, MO Xiaoyong, ZHANG Xin. Research status and application of wireless power transmission technology[J]. Proceedings of the CSEE, 2015, 35(10): 2584-2600(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.2015.10.026
[3] 朱春波, 姜金海, 宋凯, 等. 电动汽车动态无线充电关键技术研究进展[J]. 电力系统自动化, 2017, 41(2): 60-65, 72. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201702010.htm ZHU Chunbo, JIANG Jinhai, SONG Kai, et al. Research progress of key technologies for dynamic wireless charging of electric vehicle[J]. Automation of Electric Power Systems, 2017, 41(2): 60-65, 72(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201702010.htm
[4] 张波, 疏许健, 吴理豪, 等. 无线电能传输技术亟待解决的问题及对策[J]. 电力系统自动化, 2019, 43(18): 1-12. DOI: 10.7500/AEPS20181218007 ZHANG Bo, SHU Xujian, WU Lihao, et al. Problems of wireless power transmission technology urgent to be solved and corresponding countermeasures [J]. Automation of Electric Power Systems, 2019, 43(18): 1-12(in Chinese). DOI: 10.7500/AEPS20181218007
[5] ZHANG Zhen, PANG Hongliang, GEORGIADIS A, et al. Wireless power transfer-an overview[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1044-1058. DOI: 10.1109/TIE.2018.2835378
[6] 吴旭升, 孙盼, 杨深钦, 等. 水下无线电能传输技术及应用研究综述[J]. 电工技术学报, 2019, 34(8): 1559-1568. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201907001.htm WU Xusheng, SUN Pan, YANG Shenqin, et al. Review on underwater wireless power transfer technology and its application[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1559-1568(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201907001.htm
[7] 程志远, 陈坤, 李东东, 等. 旋转式无线充电系统偏移特性研究[J]. 电工技术学报, 2021, 36(22): 4648-4657. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202122003.htm CHENG Zhiyuan, CHEN Kun, LI Dongdong, et al. Research on offset characteristics of rotary wireless charging system[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4648-4657(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202122003.htm
[8] 麦瑞坤, 陈阳, 刘野然. 基于变补偿参数的IPT恒流恒压电池充电研究[J]. 中国电机工程学报, 2016, 36(21): 5816-5821. DOI: 10.13334/j.0258-8013.pcsee.152500 MAI Ruikun, CHEN Yang, LIU Yeran. Compensation capacitor alteration based ipt battery charging application with constant current and constant voltage control [J]. Proceedings of the CSEE, 2016, 36(21): 5816-5821(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.152500
[9] 戴欣, 夏梓壹, 犹安红. 多激励端WPT系统基于模型逆的输出控制[J]. 中国电机工程学报, 2022, 42(20): 7319-7331. DOI: 10.13334/j.0258-8013.pcsee.213076 DAI Xin, XIA Ziyi, YOU Anhong. Model-inverse-based output control of the multi-excitation-unit WPT system [J]. Proceedings of the CSEE, 2022, 42(20): 7319-7331(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.213076
[10] HU Jianghao, ZHAO Jiankang, CUI Chao. A wide charging range wireless power transfer control system with harmonic current to estimate the coupling coefficient [J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5082-5094. DOI: 10.1109/TPEL.2020.3032659
[11] ZHENG Peikun, LEI Wanjun, LIU Fenghua, et al. Primary control strategy of magnetic resonant wireless power transfer based on steady-state load identification method[C]//2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC). Shenzhen: IEEE, 2018: 1-5.
[12] WANG Zhihui, LI Yupeng, SUN Yue, et al. Load detection model of voltage-fed inductive power transfer system [J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5233-5243. DOI: 10.1109/TPEL.2013.2243756
[13] 苏玉刚, 陈龙, 王智慧, 等. 基于最小二乘法的感应电能无线传输系统负载辨识方法[J]. 电工技术学报, 2015, 30(5): 9-14. DOI: 10.3969/j.issn.1000-6753.2015.05.002 SU Yugang, CHEN Long, WANG Zhihui, et al. A load identification method for inductive power transfer system based on the least squares algorithm[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 9-14(in Chinese). DOI: 10.3969/j.issn.1000-6753.2015.05.002
[14] SU Yugang, ZHANG Hongyan, WANG Zhihui, et al. Steady-state load identification method of inductive power transfer system based on switching capacitors [J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6349-6355. DOI: 10.1109/TPEL.2015.2411755
[15] SHENG Xuerui, SHI Liming. Mutual inductance and load identification method for inductively coupled power transfer system based on auxiliary inverter[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1533-1541. DOI: 10.1109/TVT.2019.2962738
[16] YIN Jian, LIN Deyan, PARISINI T, et al. Front-end monitoring of the mutual inductance and load resistance in a series-series compensated wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7339-7352. DOI: 10.1109/TPEL.2015.2509962
[17] SU Yugang, CHEN Long, WU Xueying, et al. Load and mutual inductance identification from the primary side of inductive power transfer system with parallel-tuned secondary power pickup[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9952-9962. DOI: 10.1109/TPEL.2018.2793854
[18] SUN Longzhao, SUN Mingui, MA Dianguang, et al. Detecting load resistance and mutual inductance in series-parallel compensated wireless power transfer system based on input-side measurement[J]. International Journal of Antennas and Propagation, 2018, 2018: 2094637.
[19] ZHANG Yuwang, GUO Yanjie, ZHU Qingwei, et al. Load and mutual inductance estimation based on phase‐differences for electric vehicle wireless charging system [J]. IET Power Electronics, 2019, 12(9): 2345-2352. DOI: 10.1049/iet-pel.2018.5194
[20] GUO Yanjie, ZHANG Yuwang, LI Shufan, et al. Load parameter joint identification of wireless power transfer system based on the DC input current and phase-shift angle[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10542-10553. DOI: 10.1109/TPEL.2020.2981651
[21] DAI Ruimin, ZHOU Wei, CHEN Yonghong, et al. Pulse density modulation based mutual inductance and load resistance identification method for wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9933-9943. DOI: 10.1109/TPEL.2022.3153657
[22] 苏玉刚, 陈龙, 吴学颖, 等. 基于遗传算法的SS型磁耦合WPT系统负载与互感识别方法[J]. 电工技术学报, 2018, 33(18): 4199-4206. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201818004.htm SU Yugang, CHEN Long, WU Xueying, et al. Load and mutual inductance identification method of SS-type magnetically-coupled WPT system based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4199-4206(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201818004.htm
[23] 郭彦杰, 张玉旺, 王丽芳, 等. 无线电能传输系统接收端多参数联合辨识[J]. 中国电机工程学报, 2022, 42(20): 7403-7414. DOI: 10.13334/j.0258-8013.pcsee.220337 GUO Yanjie, ZHANG Yuwang, WANG Lifang, et al. Joint identification of multiple parameters in the secondary side of wireless power transfer systems[J]. Proceedings of the CSEE, 2022, 42(20): 7403-7414(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.220337
[24] GUO Yanjie, ZHANG Yuwang, ZHANG Wenjie, et al. Battery parameter identification based on wireless power transfer system with rectifier load[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 6893-6904. DOI: 10.1109/TIE.2020.3003549
[25] 米增强, 陈志忠, 南志远, 等. 同步发电机动态参数辨识[J]. 中国电机工程学报, 1998, 18(2): 100-105. DOI: 10.3321/j.issn:0258-8013.1998.02.006 MI Zengqiang, CHEN Zhizhong, NAN Zhiyuan, et al. Dynamic parameter identification of synchronous machines[J]. Proceedings of the CSEE, 1998, 18(2): 100-105(in Chinese). DOI: 10.3321/j.issn:0258-8013.1998.02.006
[26] 张猛, 肖曦, 李永东. 基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器[J]. 中国电机工程学报, 2007, 27(6): 36-40. http://ntps.epri.sgcc.com.cn/djgcxb/CN/ ZHANG Meng, XIAO Xi, LI Yongdong. Speed and flux linkage observer for permanent magnet synchronous motor based on EKF[J]. Proceedings of the CSEE, 2007, 27(6): 36-40(in Chinese). http://ntps.epri.sgcc.com.cn/djgcxb/CN/
[27] 陆华才, 徐月同. 基于AEKF的永磁直线同步电机速度和位置估计算法[J]. 中国电机工程学报, 2009, 29(33): 90-94. DOI: 10.3321/j.issn:0258-8013.2009.33.014 LU Huacai, XU Yuetong. Speed and position estimation algorithm of permanent magnet linear synchronous motor based on augmented extended Kalman filter [J]. Proceedings of the CSEE, 2009, 29(33): 90-94(in Chinese). DOI: 10.3321/j.issn:0258-8013.2009.33.014
[28] VALVERDE G, KYRIAKIDES E, HEYDT G T, et al. Nonlinear estimation of synchronous machine parameters using operating data[J]. IEEE Transactions on Energy Conversion, 2011, 26(3): 831-839. DOI: 10.1109/TEC.2011.2141136
[29] LALAMI A, WAMKEUE R, KAMWA I, et al. Unscented Kalman filter for non-linear estimation of induction machine parameters[J]. IET Electric Power Applications, 2012, 6(9): 611-620. DOI: 10.1049/iet-epa.2012.0026
[30] VAKA R, KESHRI R K. Reconfigurable WPT system for load-independent CC and CV output with transmitting- side control[J]. IET Electric Power Applications, 2020, 14(4): 685-694. DOI: 10.1049/iet-epa.2019.0406
[31] 张潇. 基于神经网络与强化学习的粒子群优化算法研究[D]. 无锡: 江南大学, 2022. ZHANG Xiao. Research on particle swarm optimization algorithm based on neural network and reinforcement learning[D]. Wuxi: Jiangnan University, 2022(in Chinese).
-
期刊类型引用(2)
1. 王得安,张剑韬,朱春波,别致,崔淑梅. 海洋环境对水下无线电能传输系统的影响机理研究进展. 电工技术学报. 2025(03): 653-675 .  百度学术
百度学术
2. 林贤宏,黄东晓,洪泽全,汪凤翔. 基于变直流母线电压的磁耦合式励磁系统控制策略研究. 微特电机. 2024(10): 31-36 .  百度学术
百度学术
其他类型引用(1)




 下载:
下载:

 下载:
下载:



