Impedance Characteristics and Detection Method of Lithium-ion Battery Under Overcharge Condition Based on Electrochemical Impedance Spectroscopy
-
摘要: 目前以锂电池为主的电化学储能单元及系统应用日益广泛，而锂电池在实际使用中频发因过充电滥用引发电池故障的情况，因此实际电池的过充电状态准确检测一直是该领域的难点和瓶颈问题。针对此，该文采用电化学阻抗谱技术对单体电池过充电行为及过程开展检测研究，在实验室设计并制定电池过充电模拟循环实验，利用弛豫时间分布法对锂电池阻抗特性进行分析；在获得电池阻抗特性的基础上，对电池弛豫时间分布曲线进行解析；最后筛选阻抗特征参量为模型输入量，构建支持向量机模型进行电池过充电检测。结果表明，弛豫时间分布曲线中的极化峰P1对应锂离子在固态电解质界面(solid electrolyte interphase，SEI)膜中的扩散过程、极化峰P2对应电子在正极材料中的扩散过程、极化峰P3对应锂离子在电极界面的氧化还原反应。过充电会导致电池欧姆内阻、SEI膜内阻与电荷转移电阻的增长速率最大为正常循环的266%、360%和182%，其中固态电解质界面SEI膜内阻为主要因素。电化学阻抗谱的阻抗特征参量以及支持向量机模型可以用于锂电池过充电检测，估计精度达93.24%。不仅可掌握电池的运行状态，还可对过充电进行有效辨识。Abstract: Currently, electrochemical energy storage units and systems utilizing lithium-ion batteries are increasingly popular, however, lithium-ion batteries frequently fail due to overcharge abuse in practical use. Therefore, accurate detection of actual battery overcharge status is always a difficult and bottleneck problem in this field. In view of this, the electrochemical impedance spectroscopy technology is used to detect and study the overcharging behavior and process of single batteries. The battery overcharging simulation cycle experiment is designed and developed in the laboratory, and the relaxation time distribution method is used to analyze the impedance characteristics of lithium battery. On the basis of obtaining the impedance characteristics of the cell, the relaxation time distribution curve of the cell is analyzed. Finally, the impedance characteristic parameter is selected as the model input, and the support vector machine model is constructed to detect the battery overcharge. The results show that the polarization peak P1 in the relaxation time distribution curve corresponds to the diffusion process of lithium ions in SEI film, peak P2 corresponds to the diffusion process of electrons in the positive electrode material, and peak P3 corresponds to the redox reaction of lithium ions at the electrode interface. Overcharging results in the growth rate of ohmic resistance, SEI film resistance and charge transfer resistance of the battery are 266%, 360% and 182% of the normal cycle, in which the SEI film resistance is the main factor. The impedance characteristic parameters of electrochemical impedance spectroscopy and the support vector machine model can be used to detect the overcharge of lithium batteries, and the estimated accuracy is 93.24%. It can not only master the running state of the battery, but also effectively identify the overcharge.
-
0. 引言
随着“双碳”目标提出，构建清洁能源综合利用和新型储能方式成为研究热点，而锂离子电池在电化学储能与新能源汽车领域有着极其重要的地位，因此也受到极其广泛的关注。锂电池在实际使用中存在过充电滥用情况，易导致电池内部结构出现变化，其宏观表现为电池老化较迅速，轻微过充电并不会导致热失控，且具有潜伏期长不易被发现等特点[1]。经多次充放电循环后，过充电的电池内部会出现微短路，若隐患进一步扩大更易导致安全事故发生，因此亟须开展电池过充电特性、状态特征及辨识等研究工作。
目前针对电池单体过充电研究主要为基于结构形态的特性分析与检测方法[2-3]，该方法虽能够清晰反映出电池的特性变化，但是观测窗口较窄，且对电池具有一定破坏性，无法对过充电演化特性进行分析。电化学阻抗谱法(electrochemical impedance spectroscopy，EIS)在宽频域范围内对电池交流内阻进行测试，不仅能实现电池的无损原位检测，还能表征电池内部不同的电化学过程[4-5]，可通过对电池不同频率的阻抗值或根据电化学阻抗谱构建的等效电路模型中与电化学过程构建对应的参数变化，实现对电池内某一电化学过程的独立分析，以有效表征电池状态。电化学阻抗谱对电池内部多个电化学反应具有同时表征的能力，如文献[6]指出各个频率下的交流阻抗值与电池内部理化特征高度相连。目前主要通过构建等效电路模型对电化学阻抗谱进行分析与解释，但当电池电化学反应过程时间常数接近时，等效电路模型则无法进行有效分析。为实现不同电化学过程的分离，研究人员提出基于时间常数的分析方法，即弛豫时间分布法(distribution of relaxation times，DRT)[7-9]。
弛豫时间分布法可计算出特征时间常数的个数及对应的频率范围[10]，因此引起研究人员的高度关注及广泛研究，具体有：1）基于锂电池状态估计，如荷电状态(state of charge，SOC)、健康状态(state of health，SOH)和内部温度估计[11-13]等；2）锂电池过充电特征辨识，如张青松[14]等对过充电电池的循环寿命变化以及电池老化特征进行研究，表明电池容量的迅速衰减是由于电池结构中活性锂离子的减少以及活性材料的损失；3）锂电池过充电检测，如Yadong Liu[15]等对过充电下锂电池进行测试，利用等效电路模型进行分析，表明电荷转移阻抗、Warburg阻抗可反映过充电，但其未考虑实际工作过程中过充电的情况，且需进行宽频带的交流内阻测试，测量时间长。Depeng Kong[16]等分析锂电池过充电内部结构变化，过充电会导致电解液氧化、金属锂析出，同时容量增量曲线中峰值出现明显变化，指出这些变化可以作为早期检测的指标，但缺乏针对电池轻微过充电老化循环过程特性的深入研究分析，且仍多借助于等效电路模型，尚未给出具体检测方法和模型。
经前述分析可知，基于电化学阻抗谱的电池过充电特性研究与检测目前仍存在以下问题：1）宽频域范围内的电化学阻抗谱分析仍借助于等效电路模型，估计及检测精度受模型精度的影响，尚无基于时间常数分析与应用的深入研究；2）现有研究多集中于严重过充电程度的分析，与实际应用存在较大差异，电池更多处于不易监测的过充电状态，目前针对电池轻度过充电下的电池机理、阻抗特性分析尚未有深入研究；3）现有电化学阻抗谱研究多是集中于机理分析，指出可用于过充电检测的特征参量，但尚未建立相关标准，缺乏普适性的检测方法与流程，且检测结果不具可比性。
针对现有研究不足，本文提出基于电化学阻抗谱的锂电池过充电检测流程与状态辨识方法，利用弛豫时间分布法对不同温度与不同荷电状态下的锂电池电化学阻抗谱进行解析，获得不同频率的交流阻抗与电池内部电化学过程间的对应关系，筛选可有效表征电池过充电的阻抗特征量，利用粒子群优化的支持向量机模型对锂电池过充电诊断方法进行研究，为电池管理系统管理策略提供理论基础。
1. 实验平台及实验方法
1.1 实验对象
本文选用松下NCR18650电池，电池正极材料由镍、钴、铝化合物构成，负极材料为石墨，其基本参数如表 1所示。
表 1 电池基本参数Table 1. Essential parameters of the battery参数类型 参数指标 参数类型 参数指标 标称容量/(mA·h) 3 300 额定电压/V 3.60 充电截止电压/V 4.20±0.03 放电截止电压/V 2.50 1.2 电池老化循环实验
1.2.1 锂电池过充电实验平台
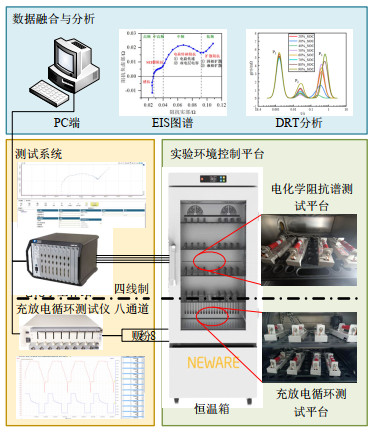
因锂电池循环老化易受环境因素影响，环境温度越高电池循环老化速率越快，且温度升高电池交流内阻会逐渐减小[12]。实验中利用NEWARE恒温箱控制锂电池过充电循环过程的温度，其恒温范围为0~60℃。利用NEWARE-BTS-5V-12A控制电池进行不同程度的过充电循环。利用PARSTAT电化学工作站对电池进行EIS测试。搭建锂电池正常与过充电循环和电化学阻抗谱实验测试平台，如图 1所示。
![]()
图 1 锂电池充放电循环和EIS实验测试平台Figure 1. Lithium batteries charge-discharge cycle test platform1.2.2 实验方法与流程
依据文献[17]，本文在电池循环实验进行如下设置。
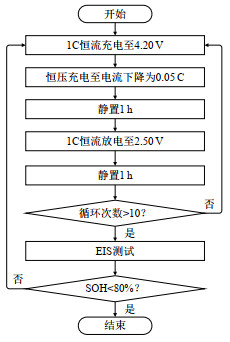
1）正常循环：将电池以1 C电流充电至4.2 V，之后恒压充电至电流下降为0.05 C，静置1 h后恒流放电至2.5 V，如此往复，每10次循环后对电池进行容量标定和不同SOC下的EIS测试，具体实验流程与步骤如图 2所示。
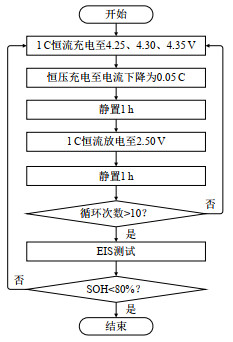
2）过充电循环：以1 C电流恒流充电至不同电压(4.25、4.30、4.35V)，之后恒压充电至电流下降为0.05 C，静置1 h后恒流放电至2.5 V，如此往复，每10次过充电循环后对电池进行容量标定和不同SOC下的EIS测试，具体实验流程与步骤如图 3所示。容量标定步骤：在25℃下，以0.5 C电流恒流充电至4.2 V，之后恒压充电至电流为0.05 C，静置1 h后再以0.2 C电流恒流放电至2.5 V，循环进行3次，取平均值作为电池当前容量。
2. 电化学阻抗谱弛豫时间分布曲线解析
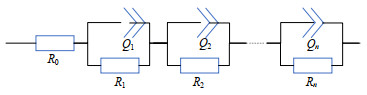
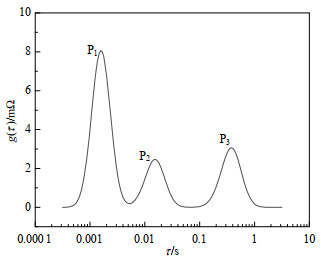
锂离子电池的内部电化学过程可利用电化学阻抗谱进行表征，文献[5]研究表明，中高频区(频率为1~1 000 Hz)半圆表示电池内部的极化过程，主要包含电子在正极活性材料中的扩散过程(电荷转移阻抗)、锂离子在固态电解质界面(solid electrolyte interphase，SEI)膜的传递(SEI膜阻抗)以及电极处的氧化还原过程(电荷传递阻抗)。但中高频区所包含电化学极化过程由于时间常数相近，往往难以准确区分，无法研究每个电化学反应过程随电池过充电循环次数增加所对应的阻抗变化，因此需要对电化学阻抗谱进行解谱，对不同过程解析。本文采用弛豫时间分布法，利用如图 4所示的多个串联RQ回路，来描述电池内部不同弛豫时间的电化学反应数量以及诸多极化过程[18]。进行DRT计算时筛除EIS的超高频与低频部分，对中高频区半圆进行反卷积运算，获得锂电池弛豫时间分布函数，50%SOC下的DRT曲线如图 5所示。
![]()
图 5 50%SOC时锂电池电化学阻抗谱DRT分析Figure 5. Electrochemical impedance spectroscopy DRT analysis of lithium battery under 50%SOC弛豫时间分布曲线存在P1、P2、P3这3个极化峰，对应电池中高频区的3个极化过程，即前文所述的电子在正极活性材料中的扩散过程、锂离子在SEI膜的扩散过程以及锂离子在电极界面处的溶剂化与去溶剂化过程，但不确定一一对应关系。由式(1)可得，DRT曲线中不同极化过程所对应极化峰包络的面积为该过程的极化内阻。为研究过充电循环过程中的阻抗特性，需要对弛豫时间分布中的极化峰与电池内部电化学反应过程进行对应求解。
$$ Z(\omega ) = {R_0} + {Z_{{\text{pol}}}}(\omega ) = {R_0} + {R_{{\text{pol}}}}\int_0^\infty {\frac{{g(\tau )}}{{1 + {\text{j}}\omega \tau }}{\text{d}}\tau } $$ (1) 式中：Z(ω)为电池的总阻抗；R0为电池的欧姆内阻；Zpol(ω)为电池的总极化阻抗；Rpol为电池的极化电阻；g(τ)为弛豫时间分布函数；τ为弛豫时间；j为复数单位；ω为角频率。
为有效区分锂电池弛豫时间分布曲线中的3个极化过程，本文在不同工作温度(15、25、35、45℃)与不同SOC(10%~90%)下对电池进行电化学阻抗谱测试，以此分析不同状态下DRT曲线，实现极化过程与极化峰间的对应。
2.1 不同温度下的DRT曲线解析
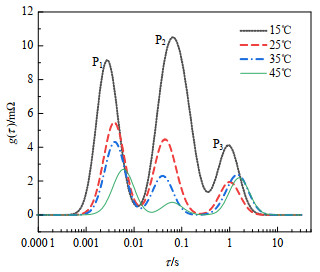
为控制其他因素的影响，对50%SOC的锂电池进行不同温度下的电化学阻抗谱测试，并计算弛豫时间分布如图 6所示。
![]()
图 6 50%SOC下锂电池不同温度的DRT分析Figure 6. DRT analysis of lithium battery at different temperature under 50%SOC由图 6可知，随着温度升高，极化峰P1与P2峰值与所包围的面积逐渐减小，但是极化峰P3温度变化呈现不规律变化。求解3种极化过程所对应的电化学电阻表达式，以探究温度的影响。电子在正极材料中的扩散过程对应为电化学阻抗谱中的半圆，其等效电路为Re//Qe，其中Re为电荷转移电阻，表征电子在正极材料中扩散至嵌锂位的过程。根据文献[5]中电池内部的电化学反应表达式的推导可以得出，电阻表达式为
$$ {R_{\text{e}}} = \frac{S}{{\sigma L}} $$ (2) 式中：S为材料表面积；σ为材料电导率；L为材料厚度。
σ与温度的计算关系为
$$ \sigma = {\sigma _0}{{\text{e}}^{ - H/(RT)}} $$ (3) 式中：σ0为指前因子；H为带电粒子导电活化能；R为摩尔常数；T为温度。
结合式(2)与(3)，并对等式两边进行指数变换可得：
$$ \ln {R_{\text{e}}} = \ln \frac{S}{{{\sigma _0}L}} + \frac{H}{{RT}} $$ (4) 可知，lnRe与T−1之间存在线性关系。
而SEI膜电阻与温度也存在相关性，根据锂离子在固态电解质界面膜内的扩散迁移过程的动力学，其迁移电流可表示为
$$ i = 4zFacv \times {{\text{e}}^{ - W/(RT)}} \times \sinh \frac{{azFE}}{{RT}} $$ (5) 式中：z为离子电荷，锂离子z=1；F为法拉第常数；a为离子的跳跃半距离；c为离子的浓度；v为晶格振动频率；W为离子跳跃能垒；E为电场强度。
锂离子在SEI膜中扩散迁移时，SEI膜两端存在电势差，可通过电场强度计算得到η=El。其中，η为SEI膜上电势差；l为SEI膜厚度。从而得到SEI膜电阻：
$$ {R_{{\text{SEI}}}} = \frac{{RTl}}{{4{z^2}{F^2}{a^2}cv}}{{\text{e}}^{W/(RT)}} $$ (6) 由式(6)可以看出，与电荷转移电阻Re相似，lnRSEI与T−1近似呈线性关系。
电荷传递电阻Rct所表征的锂离子溶剂化与去溶剂化过程，根据正向反应与逆向反应的反应速率可得：
$$ {i_0} = nF{c_{\text{T}}}{k_0}{[{M^ + }]^{(1 - \alpha )}}{(1 - x)^{(1 - \alpha )}}{x^\alpha } $$ (7) 式中：n为电子数；cT为锂离子嵌入浓度；k0为标准反应速率常数；[M+]表示界面处电解液的锂离子浓度；α为电化学反应因子；x为嵌锂度。
其中标准反应速率常数为
$$ {k_0} = k_{\text{f}}^{\text{0}} \times {{\text{e}}^{ - [\alpha (nF{E_0} + \Delta {G_{\text{int} }})]/(RT)}} $$ (8) 电荷传递电阻被定义为
$$ {R_{{\text{ct}}}} = RT/(nF{i_0}) $$ (9) 由此可得：
$$ \begin{gathered} {R_{{\text{ct}}}} = \frac{{RT}}{{{n^2}{F^2}{c_{\text{T}}}{A_{\text{f}}}{{[{M^ + }]}^{(1 - \alpha )}}{{(1 - x)}^{(1 - \alpha )}}{x^\alpha }}} \times \\ {{\text{e}}^{\frac{{\Delta {G_{{\text{oc}}}} + \alpha (nF{E_0} + \Delta {G_{{\text{int}}}})}}{{RT}}}} \\ \end{gathered} $$ (10) 由式(10)可见，电荷传递电阻Rct与温度间未存在规律的函数关系，因此图 6中极化峰P3所对应的极化过程为锂离子的溶剂化/去溶剂化过程，所包围面积为电荷传递电阻。
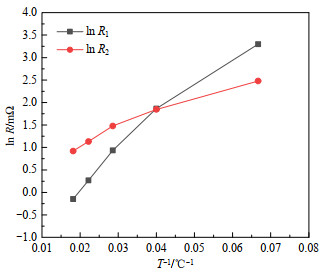
对图 6中极化峰P1、P2所包围面积即各个极化电阻的阻值进行求解，并计算lnR与T−1的关系，如图 7所示，lnR1与lnR2与T−1间的相关系数分别为0.983 4及0.988 6。由此可得极化峰P1与P2对应SEI膜扩散过程与电荷转移过程，但仍无法确定极化峰P1、P2与上述两过程间的对应关系。
2.2 不同SOC下的DRT曲线解析
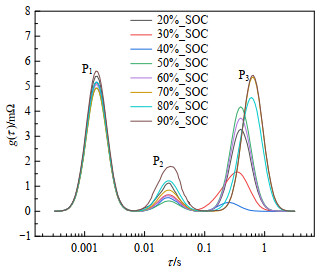
为有效区分极化峰P1、P2与极化过程之间的对应关系，在25℃下对电池不同SOC(90%, 80%, …, 10%)进行EIS测试。对中高频区的交流阻抗进行弛豫时间分布分析，如图 8所示。随着SOC的变化，极化峰P1峰值与峰所包络的面积基本保持不变，极化峰P2在高SOC与低SOC时，峰值及曲线所包围的面积较大。电池SOC的高低代表电极处嵌入锂离子的浓度大小，也表示电极极化电位的高低。由式(5)、(6)推导过程可知，SEI膜电阻基本不会受到电极极化电位的影响，因此极化峰P1对应锂离子在SEI膜中的扩散迁移过程，极化峰P2对应电子在正极活性材料中的扩散过程。
![]()
图 8 25℃下锂电池不同SOC的DRT分析Figure 8. DRT analysis of lithium battery at different SOC under 25℃极化峰P2对应的极化电阻随SOC升高先增大后减小。这是由于在高SOC下，大量锂离子脱嵌，正极材料中Mn3+会氧化为Mn4+，电子扩散迁移的载流子数量下降，导致电导率下降，电阻增大；在低SOC时，由于锂离子大量嵌入正极材料，已有大量电子迁移至嵌锂位，使得后续电子的扩散迁移过程变得更为困难，电阻随之增大。
由不同温度与不同SOC下电池电化学阻抗谱的弛豫时间分布可得，弛豫时间分布曲线中的3个峰，极化峰P1对应锂离子在SEI膜的扩散过程，极化峰P2对应电子在正极材料中的扩散过程，极化峰P3对应锂离子在电极界面的溶剂/去溶剂化过程。
3. 锂电池过充电阻抗特性与检测分析
3.1 锂电池过充电中高频区阻抗特性分析
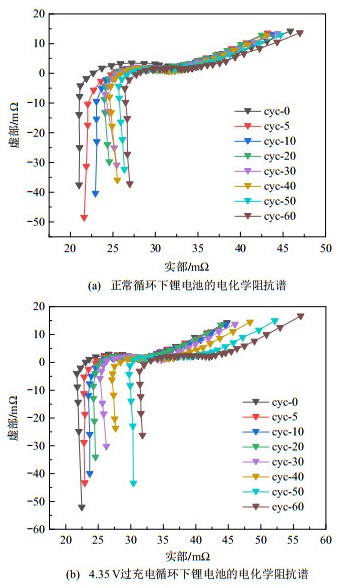
记录电池正常与过充电循环在不同循环次数下的电化学阻抗谱，如图 9所示。
![]()
图 9 不同循环次数下正常循环与过充电循环的锂电池电化学阻抗谱Figure 9. Electrochemical impedance spectroscopy of lithium batteries with normal cycles and overcharge cycles under different cycle times由图 9可见，随着循环次数的增加，正常与过充电循环其奈奎斯特曲线均右移，实部增长，虚部基本保持不变，并且在相同循环次数下过充电循环实部增长明显大于正常循环，且两者在中高区均呈现为一个“半圆”，本节通过弛豫时间分布法对电化学阻抗谱进行处理与解析。
通常将电化学阻抗谱曲线与实轴交点的横坐标作为欧姆内阻，中高频区所对应电化学过程的极化内阻由弛豫时间分布法计算求得。
$$ {R_{{\text{pol}}}} = \int_{{\tau _{\text{L}}}}^{{\tau _{\text{H}}}} {\gamma (\tau ){\text{d}}\tau } $$ (11) 式中：Rpol为极化过程所对应的极化内阻值；τH为极化峰对应的最大时间常数；τL为极化峰对应的最小时间常数；γ为极化过程所对应的时间常数表达式；τ为时间常数。
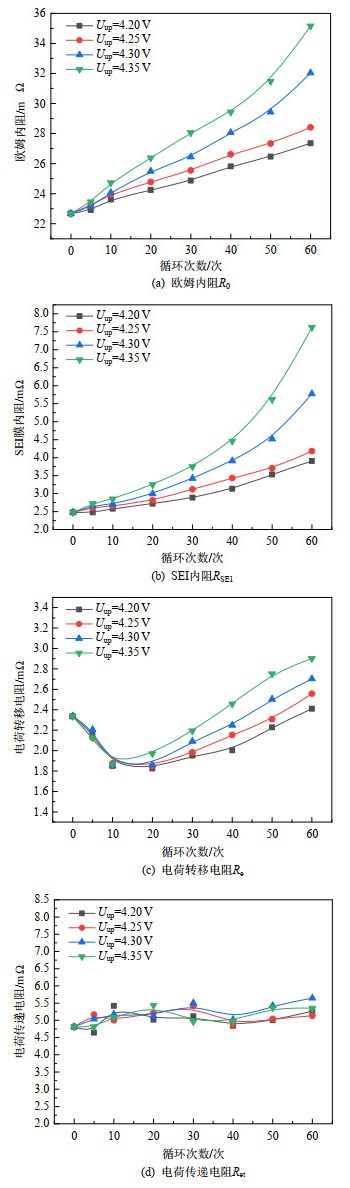
对不同次数正常与过充电循环锂电池电化学阻抗谱进行弛豫时间分布分析，并对极化峰面积进行求解，分别计算欧姆内阻R0与其他3个极化过程对应的极化内阻，如图 10所示。
![]()
图 10 正常循环与过充电循环的锂电池中高频区电化学反应极化电阻值Figure 10. Electrochemical reaction polarization resistance values in the middle and high frequency region of normal and overcharged lithium batteries由图 10(a)可知，随着循环次数的增加，锂电池欧姆内阻逐渐增大。这是由于在电池循环中，锂离子嵌入与脱嵌次数增多，导致活性材料颗粒间隙增大，从而导致电导率下降。过充电Uup=4.30 V与Uup=4.35 V欧姆内阻增长迅速，且表现出两个阶段，40次循环后增长加快。Uup=4.35 V欧姆内阻增长速率为正常循环的2.66倍。究其原因，锂电池在过充电-放电循环过程中，由于石墨负极活性材料所能嵌入的锂离子有限，在石墨负极处锂离子被氧化还原为锂金属，电池内部出现微短路。微短路引起电池充放电过程温度上升，进而使得电解液分解产生气体[19]，阻碍锂离子的扩散，使得欧姆内阻增大。
由图 10(b)可见，随着循环次数的增加，正常与过充电循环的SEI膜内阻在初始循环(20次以内)均增长不明显，之后随着循环次数增加，其增大幅度逐渐增加。随着循环次数增加，SEI膜会逐渐增厚，从而导致锂电池SEI膜内阻随循环次数增加而增加。Uup=4.30V与Uup=4.35V过充电循环在初始循环阶段与正常循环类似，但循环次数增加后，其SEI膜内阻大于正常循环，增长速率最大可达360%。这是由于在较高截止电压的过充电循环中，负极石墨颗粒所能嵌入锂离子的数量有限，过量嵌入的锂离子使得石墨颗粒体积膨胀，导致SEI膜出现“裂纹”，导致石墨电极与电解液接触反应生成SEI膜，并且锂枝晶自裂纹处“生长”，因此出现过充电循环SEI膜内阻大于正常循环[15]。
由图 10(c)发现，随着循环次数的增加，电荷转移电阻均呈现出先减小再增大的现象。在初始循环(0~10次)内，随着充放电的进行，正负电极中更多的活性颗粒参与锂离子的嵌入与脱嵌，电荷转移内阻出现下降。但随着循环次数增多，SEI膜增厚以及电极活性材料活性下降，阻值又会逐渐增大。过充电循环中截止电压越高，嵌入与脱嵌过程中参与反应的锂离子与正负极活性颗粒就越多，因此其电荷转移内阻增长幅度远大于正常循环，Uup=4.35V下增长幅度为182%。
由图 10(d)可见，电荷传递电阻在一定范围内波动，在电池正常与过充电循环均未有明显变化。证明正常与过充电循环仅影响电极材料与电解液特性，不会对锂电池电极界面反应造成影响。
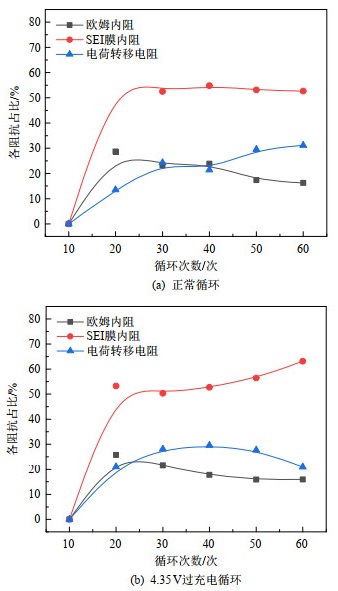
上述4个电阻参数中，随着充电循环电荷传递电阻在60次循环中没有明显变化，电荷转移电阻先下降后上升，因此，从第10次循环开始，计算欧姆内阻、SEI膜内阻、电荷转移电阻在阻值上升阶段贡献的占比如式(12)所示，以分析过充电循环对电池电化学反应过程的影响。正常与过充电循环的锂电池中高频区各电阻值占比如图 11所示，SEI膜内阻所占比例最大，且在过充电循环下，其占比随着循环次数逐渐升高，因此轻微过充电对锂离子在SEI膜中的扩散迁移过程影响最大。
$$ {P_i}^{n = x} = \frac{{(R_i^{n = x} - R_i^{n = 10})/R_i^{n = 10}}}{{\sum\limits_{i = 1}^3 {[(R_i^{n = x} - R_i^{n = 10})/R_i^{n = 10}]} }} \times 100\% $$ (12) ![]()
图 11 正常循环与过充电循环的锂电池中高频区各电阻值占比Figure 11. Ratio of resistance values in the middle and high frequency region of normal and overcharged lithium batteries式中：Ri为电阻值；x为循环次数；P为各电阻值在不同循环次数下的占比。
3.2 锂电池过充电检测模型
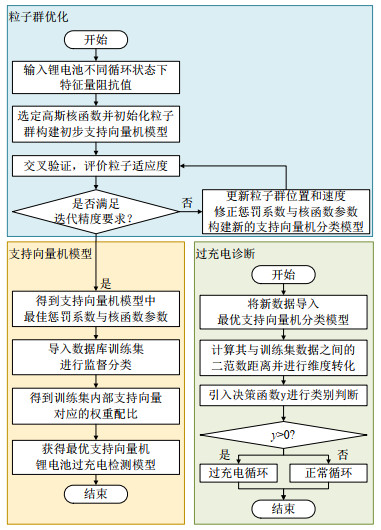
本节以锂电池正常循环与过充电循环的阻抗特性数据作为驱动，通过基于粒子群优化的支持向量机分类算法建立锂电池过充电检测模型[20-21]，整体诊断分析流程如图 12所示，主要步骤如下。
![]()
图 12 基于粒子群优化的支持向量机诊断模型流程图Figure 12. Flow chart of support vector machine diagnosis model based on particle swarm optimization1）根据锂电池过充电阻抗特性分析，确定支持向量机输入量的维数。
2）选择核函数(本文以高斯函数作为核函数)，初始化粒子群，设置粒子群体规模、惩罚值、迭代最大次数、核函数的初始参数值，以粒子的横纵坐标分别表征支持向量机模型中的惩罚系数与核函数参数。
3）进行粒子群优化：根据参数建立初步支持向量机分类模型筛选最优惩罚系数与核函数参数，将已有数据作为训练集导入模型中进行交叉验证，计算每个粒子的适应度函数，通过更新粒子的位置与速度确定新的参数，从而构建新的支持向量机诊断模型。
4）判断当迭代次数达到最大迭代次数或群体最优值达到精度要求值，即n次计算的适应度函数最大值与(n−1)次适应度函数最大值相等，最后获得粒子群体最优位置，得到能够区分正常与过充电下锂电池阻抗特性的最优参数。
5）将训练集导入具备最优参数的支持向量机模型中进行训练，进一步得到训练集内部各组数据对应的权重配比，构建最优的支持向量机锂电池过充电检测模型。
电池不同SOC使电化学阻抗谱产生偏移，因而特征参量值存在差异。本文对20%、50%、80%SOC下[22]的锂电池分别进行电化学阻抗谱测试和弛豫时间分布分析，并将其阻抗特征参量均纳入数据驱动的考虑范围内，使过充电检测模型可以在不同的SOC阶段下均可使用。
为实现锂电池过充电检测，需要提取能够有效表征过充电的特征参量，在3.1节中对25℃、80%SOC下锂电池过充电与正常循环的极化电阻变化规律进行分析，发现相较于正常循环，在过充电下，其欧姆内阻、SEI膜内阻、电荷转移电阻均增大，而电荷传递电阻未有明显变化。
因此，为有效区分过充电锂电池，本节所建立的模型以欧姆内阻R0、SEI膜内阻RSEI与电荷转移电阻Re的值为特征量。为后续算法计算方便，将过充电循环标签设置为“1”，正常循环标签设置为“2”。电池老化实验中25℃、80%SOC下部分过充电与正常循环数据样本分别如表 2、3所示。
表 2 4.35 V过充电循环锂电池特征参量值(label=1)Table 2. Characteristic parameter values of 4.35 V overcharge cycles lithium battery(label=1)SOH R0 RSEI Re SOH R0 RSEI Re 100.00% 22.95 2.31 2.21 93.13% 27.05 3.75 1.96 99.52% 23.46 2.72 2.13 88.78% 28.43 4.46 2.46 98.66% 24.73 2.85 1.47 83.48% 30.47 5.51 3.23 96.04% 26.39 3.25 1.57 77.23% 33.06 6.62 3.36 表 3 正常循环锂电池的特征参量值(label=2)Table 3. Characteristic parameter values of normal cycles lithium battery(label=2)SOH R0 RSEI Re SOH R0 RSEI Re 100.00% 22.91 2.28 2.24 92.49% 27.36 4.11 2.51 99.25% 23.62 2.61 1.47 90.67% 28.26 4.53 2.70 98.03% 24.25 2.76 1.30 89.07% 28.99 5.42 2.83 97.20% 24.87 2.89 1.69 87.94% 29.39 7.77 3.28 96.06% 25.83 3.23 1.69 86.78% 29.98 7.96 3.56 94.41% 26.47 3.73 2.13 82.61% 30.54 8.21 4.23 模型中所采用的粒子群优化算法学习因子初始值设置为c1=1.5，c2=1.6，最大迭代次数maxgen=50，种群规模设置sizepop=20.00。粒子横坐标，即惩罚系数c取值区间为[0.1, 1 000]；粒子纵坐标，核函数参数γ取值区间为[0.01, 1 000]。通过种群粒子位置不断优化，最终确定支持向量机模型中与训练数据适配程度最高的惩罚系数和核函数参数。
电池不同循环次数的过充电与正常循环数据共1 207组，随机抽取1 000组作为支持向量机分类模型的训练数据集进行输入，剩余207组作为模型测试集检验模型分类效果。将待诊断的阻抗特性数据导入分类模型时，通过计算其与训练集数据之间的二范数距离并进行维度转化，如式(13)和(14)所示，以便将其代入决策函数进行类别判断，如式(15)所示。
$$ \left\| {x - {x_i}} \right\| = \sqrt {\sum\limits_{j = 1}^{l(x)} {|{x^{(j)}} - x_i^{(j)}{|^2}} } $$ (13) $$ k(x,{x_i}) = {{\text{e}}^{( - \gamma {{\left\| {x - {x_i}} \right\|}^2})}} $$ (14) $$ y = \sum\limits_{i \in S} {{\alpha _i}k(x,{x_i}) + c} $$ (15) 式中：x为待诊断的阻抗特性数据；xi为训练集中阻抗特性数据；l(x)为阻抗特性数据的维度，为3；γ为核函数参数；S为支持向量集；c为惩罚系数，二者均通过粒子群优化算法得到最优解；αi为不同支持向量的权重配比，由支持向量机自身训练得到；y为最终分类决策结果，y > 0代表该组锂电池属于过充电类型，y < 0则代表其属于正常类型。
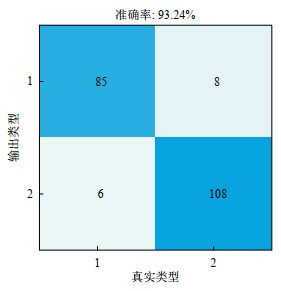
基于粒子群优化的支持向量机模型，其最终测试集诊断分类的混淆矩阵，如图 13所示。在测试集的207组阻抗数据中，193组诊断结果与实际情况相同，模型测试集正确率可达93.24%。证明锂电池弛豫时间分布的特征量可以有效对电池的过充电进行检测，以及粒子群优化的支持向量机模型可以应用到锂电池过充电故障检测中。
4. 结论
本文利用电化学阻抗谱对锂电池过充电特性进行研究，利用弛豫时间分步法进行解析，实现对锂电池过充电的检测方法，得到如下主要结论：
1）通过分析不同温度与不同SOC下电池的电化学阻抗谱弛豫时间分布曲线，发现DRT曲线中极化峰与中高频区极化过程存在对应关系：极化峰P1对应锂离子在SEI膜的扩散过程，极化峰P2对应电子在正极半导体活性材料中扩散迁移过程，极化峰P3对应锂离子在电极界面的溶剂/去溶剂化过程。
2）通过求解不同极化过程极化内阻，分析锂电池过充电阻抗特性，过充电锂电池的欧姆内阻、SEI膜内阻与电荷转移电阻最大增长速率分别为正常循环的266%、360%和182%，电荷传递电阻无明显变化，其中SEI膜内阻是主要因素。
3）筛选出能够表征锂电池过充电的阻抗特征量，以欧姆内阻R0、SEI膜内阻RSEI与电荷转移阻抗Re为特征参量，利用粒子群优化的支持向量机模型对锂电池过充电进行检测，估计精度达93.24%。表明电化学阻抗谱的阻抗特征参量以及支持向量机模型可以用于锂电池过充电检测。
本文目前仅针对电池过充电循环的阻抗特性进行分析，利用这些特性进行过充电检测方法的研究，给电池管理系统提供更加精确的管理策略值得后续进一步探究。
-
![]()
图 1 锂电池充放电循环和EIS实验测试平台
Figure 1. Lithium batteries charge-discharge cycle test platform
![]()
图 5 50%SOC时锂电池电化学阻抗谱DRT分析
Figure 5. Electrochemical impedance spectroscopy DRT analysis of lithium battery under 50%SOC
![]()
图 6 50%SOC下锂电池不同温度的DRT分析
Figure 6. DRT analysis of lithium battery at different temperature under 50%SOC
![]()
图 8 25℃下锂电池不同SOC的DRT分析
Figure 8. DRT analysis of lithium battery at different SOC under 25℃
![]()
图 9 不同循环次数下正常循环与过充电循环的锂电池电化学阻抗谱
Figure 9. Electrochemical impedance spectroscopy of lithium batteries with normal cycles and overcharge cycles under different cycle times
![]()
图 10 正常循环与过充电循环的锂电池中高频区电化学反应极化电阻值
Figure 10. Electrochemical reaction polarization resistance values in the middle and high frequency region of normal and overcharged lithium batteries
![]()
图 11 正常循环与过充电循环的锂电池中高频区各电阻值占比
Figure 11. Ratio of resistance values in the middle and high frequency region of normal and overcharged lithium batteries
![]()
图 12 基于粒子群优化的支持向量机诊断模型流程图
Figure 12. Flow chart of support vector machine diagnosis model based on particle swarm optimization
表 1 电池基本参数
Table 1 Essential parameters of the battery
参数类型 参数指标 参数类型 参数指标 标称容量/(mA·h) 3 300 额定电压/V 3.60 充电截止电压/V 4.20±0.03 放电截止电压/V 2.50 
下载: 导出CSV
表 2 4.35 V过充电循环锂电池特征参量值(label=1)
Table 2 Characteristic parameter values of 4.35 V overcharge cycles lithium battery(label=1)
SOH R0 RSEI Re SOH R0 RSEI Re 100.00% 22.95 2.31 2.21 93.13% 27.05 3.75 1.96 99.52% 23.46 2.72 2.13 88.78% 28.43 4.46 2.46 98.66% 24.73 2.85 1.47 83.48% 30.47 5.51 3.23 96.04% 26.39 3.25 1.57 77.23% 33.06 6.62 3.36
下载: 导出CSV
表 3 正常循环锂电池的特征参量值(label=2)
Table 3 Characteristic parameter values of normal cycles lithium battery(label=2)
SOH R0 RSEI Re SOH R0 RSEI Re 100.00% 22.91 2.28 2.24 92.49% 27.36 4.11 2.51 99.25% 23.62 2.61 1.47 90.67% 28.26 4.53 2.70 98.03% 24.25 2.76 1.30 89.07% 28.99 5.42 2.83 97.20% 24.87 2.89 1.69 87.94% 29.39 7.77 3.28 96.06% 25.83 3.23 1.69 86.78% 29.98 7.96 3.56 94.41% 26.47 3.73 2.13 82.61% 30.54 8.21 4.23
下载: 导出CSV
-
[1] 王其钰, 李泓. 锂电池安全问题及失效分析[J]. 新能源科技, 2021(11): 15-19. https://www.cnki.com.cn/Article/CJFDTOTAL-JSQG202111007.htm WANG Qiyu, LI Hong. Safety and failure analysis of lithium battery[J]. New Energy Science and Technology, 2021(11): 15-19 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSQG202111007.htm
[2] 李文俊, 褚赓, 彭佳悦, 等. 锂离子电池基础科学问题(Ⅻ)—表征方法[J]. 储能科学与技术, 2014, 3(6): 642-667. https://www.cnki.com.cn/Article/CJFDTOTAL-CNKX201502027.htm LI Wenjun, CHU Geng, PENG Jiayue, et al. Basic scientific problems of lithium ion battery (Ⅻ) —characterization method[J]. Energy Storage Science and Technology, 2014, 3 (6): 642-667 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CNKX201502027.htm
[3] CHEN Y. Recent advances of overcharge investigation of lithium-ion batteries[J]. Ionics, 2022, 28(2): 495-514. DOI: 10.1007/s11581-021-04331-3
[4] MA K, QIN BY, WANG XW. Understanding the impedance of CNOs-Graphene hybrid electrode through both experimental and simulated electrochemical impedance spectrum[J]. Electrochimica Acta, 2021, 371(39): 137839.
[5] 庄全超, 杨梓, 张蕾, 等. 锂离子电池的电化学阻抗谱分析研究进展[J]. 化学进展, 2020, 32(6): 761-791. https://www.cnki.com.cn/Article/CJFDTOTAL-HXJZ202006007.htm ZHUANG Quanchao, YANG Zi, ZHANG Lei, et al. Research progress on diagnosis of electrochemical impedance spectroscopy in lithium-ion batteries[J]. Progress in Chemistry, 2020, 32(6): 761-791 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HXJZ202006007.htm
[6] CIUCCI F. Modeling electrochemical impedance spectroscopy[J]. Current Opinion in Electrochemistry, 2019, 2(13): 132-139.
[7] BERNARD B A. Fourier transform distribution function of relaxation times; application and limitations[J]. Electrochemica Acta, 2015, 154(1): 35-46.
[8] Hershkovitz S, Tomer S, Baltianski S, et al. Impedance spectroscopy analysis using evolutionary programming procedure[M]. ECS Transactions, 2011, 33(40): 67-73.
[9] 王晟, 闫帅, 李浩秒, 等. 基于正则化方法的电池阻抗谱弛豫时间分布解析[J]. 中国电机工程学报, 2022, 42(9): 3177-3188. DOI: 10.13334/j.0258-8013.pcsee.201844 WANG Sheng, YAN Shuai, LI Haosiu, et al. Analysis of relaxation time distribution of battery impedance spectrum based on regularization method[J]. Proceedings of the CSEE, 222, 42(9): 3177-3188 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.201844
[10] ILLIG J, SCHMIDT J P, WEISS M, et al. Understanding the impedance spectrum of 18650 LiFePO4-cells[J]. Journal of Power Sources, 2013, 239(1): 670-679.
[11] CARTHY K M, GULLAPALLI H, RYAN K M, et al. Review—use of impedance spectroscopy for the estimation of li-ion battery state of charge, state of health and internal temperature[J]. Journal of The Electrochemical Society, 2021, 168(8): 080517 (21pp).
[12] 范文杰, 徐广昊, 于泊宁, 等. 基于电化学阻抗谱的锂离子电池内部温度在线估计方法研究[J]. 中国电机工程学报, 2021, 41(9): 3283-3293. DOI: 10.13334/j.0258-8013.pcsee.201740 FAN Wenjie, XU Guanghao, YU Boning, et al. On-line estimation method for internal temperature of lithium-ion battery based on electrochemical impedance spectroscopy [J]. Proceedings of the CSEE, 2021, 41(9): 3283-3293 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.201740
[13] 董明, 范文杰, 刘王泽宇, 等. 基于特征频率阻抗的锂离子电池健康状态评估[J]. 中国电机工程学报, 2022, 42(24): 9094-9105. DOI: 10.13334/j.0258-8013.pcsee.212036 DONG Ming, FAN Wenjie, LIU Wangzeyu, et al. Health evaluation of lithium-ion battery based on characteristic frequency impedance[J]. Proceedings of the CSEE, 2022, 42(24): 9094-9105 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.212036
[14] 张青松, 赵启臣. 过充循环对锂离子电池老化及安全性影响[J]. 高电压技术, 2020, 46(10): 3390-3397. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ202010005.htm ZHANG Qingsong, ZHAO Qichen. Effect of overcharging cycle on aging and safety of lithium ion battery[J]. High Voltage Technology, 2020, 46 (10): 3390-3397 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ202010005.htm
[15] LIU Y, XIE J. Failure study of commercial LiFePO4 cells in overcharge conditions using electrochemical impedance spectroscopy[J]. Journal of The Electrochemical Society, 2015, 162(10): A2208-A2217. DOI: 10.1149/2.0911510jes
[16] KONG DP, WEN RX, PING P, et al. Study on degradation behavior of commercial 18650 LiAlNiCoO2 cells in over-charge conditions[J]. International Journal of Energy Research, 2019, 43(1): 552-567. DOI: 10.1002/er.4302
[17] XU F, HE H, LIU YD, et al. Failure investigation of LiFePO4 cells under overcharge conditions[J]. ECS Transactions, 2011, 195(5): A678-A687.
[18] 王春林, 朱广焱, 张鹏博, 等. 弛豫时间分布函数应用于电化学阻抗谱分析[J]. 电源技术, 2021, 45(12): 1569-1572+1593. https://www.cnki.com.cn/Article/CJFDTOTAL-DYJS202112014.htm WANG Chunlin, ZHU Guangyan, ZHANG Pengbo, et al. Application of relaxation time distribution function to electrochemical impedance spectroscopy[J]. Power supply technology, 2021, 45 (12): 1569-1572+1593 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DYJS202112014.htm
[19] 王铭民, 孙磊, 郭鹏宇, 等. 基于气体在线监测的磷酸铁锂储能电池模组过充热失控特性[J]. 高电压技术, 2021, 47(1): 279-286. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ202101030.htm WANG Mingmin, SUN Lei, GUO Pengyu, et al. Thermal runaway characteristics of lithium iron phosphate energy storage battery module based on gas on-line monitoring[J]. High Voltage technology, 2021, 47 (1): 279-286 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ202101030.htm
[20] 姜雯. 基于改进粒子群算法的SVM参数优化及应用[D]. 镇江: 江苏科技大学, 2020. JIANG Wen. Optimization and application of SVM parameters based on improved particle swarm optimization algorithm[D]. Zhenjiang: Jiangsu University of Science and Technology, 2020 (in Chinese).
[21] 刘冬梅, 霍龙龙, 王浩然, 等. 基于PSO-SVM的电流放大器故障诊断研究[J]. 传感器与微系统, 2021, 40(8): 50-56. https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ202108014.htm LIU Dongmei, HUO Longlong, WANG Haoran, et al. Current amplifier fault diagnosis based on PSO-SVM[J]. Sensors and Microsystems, 2021, 40 (8): 50-56 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ202108014.htm
[22] 张家昌. 基于深度神经网络的电动汽车单体电池故障诊断研究[D]. 重庆: 重庆邮电大学, 2020. ZHANG Jiachang. Research on single battery fault diagnosis of electric vehicle based on deep neural network [D]. Chongqing: Chongqing University of Posts and Telecommunications, 2020 (in Chinese).
-
期刊类型引用(3)
1. 刘宝泉，曹小雨. 锂电池热失控早期典型气体精准检测方法. 储能科学与技术. 2024(06): 1995-2009 . 
百度学术
2. 孟国栋，李雨珮，唐佳，顾颐，金阳，陈欣，成永红. 锂离子电池储能电站的热失控状态检测与安全防控技术研究进展. 高电压技术. 2024(07): 3105-3127 . 百度学术
3. 陈宝辉，邓捷，陆佳政，周天念，李明明，谢林瑾. 磷酸铁锂电池储能舱热失控监测传感器有效性评价及探测策略. 高电压技术. 2024(08): 3463-3477 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
- 被引次数: 5
下载:
