0.   引言

我国电网正逐步向以海上风电为代表的新型电力系统发展，无论是采用交流方式还是直流方式将大规模海上风电输送到陆上交流电网，都是通过电力电缆实现的^[1-2]。新型电力系统中变流器、可再生能源机组和交直流电网间的相互作用会使系统中产生不同于传统电力系统的宽频振荡，同时由于电缆线路中分布电容不可忽略，会增加电力系统发生宽频谐振的风险^[3-5]。

电力电缆本身具有分布参数特性，同时其在不同频率下将呈现出不同的传输特性，因此在高频下对输电线路的建模难度很大。现有对宽频谐振问题的研究中电力电缆的建模方式多未考虑其分布参数特性和参数频变特性，会影响时域仿真和稳定性评估的准确性和有效性。为研究在新场景下电缆线路的建模方式，不但要对电缆各谐波频段的电气参数进行研究，还需考虑实际工程情况选取合适的建模方式。

现有电缆参数的研究主要针对工频电气参数，对广泛应用于海上风电并网的电力电缆在高频下的电气参数鲜有提及。文献[6]基于电磁暂态仿真程序EMTP对500 kV XLPE海底电缆的电气参数在工频进行计算分析；文献[7]在此基础上结合实际工程中电缆的结构参数，对电力电缆的电气参数及其不平衡度进行分析，但它们都只考虑了工频情况；文献[8-9]根据广泛应用于工程中的电缆结构，使用简明的公式计算电缆各层结构的电气参数，但该方法的物理意义不明确，计算结果与业界广泛认可的电磁暂态仿真软件PSCAD/EMTDC间有一定的偏差。

对于传输线的建模方式，主要有集总参数模型和分布参数模型两种方式。文献[10-11]通过串联多个π型等值电路对电缆进行简化来分析系统的高频谐振，但其未考虑电缆电气参数的频变特性，串联多个π型等值电路会降低时域仿真的效率，同时可能会引起系统的虚值振荡^[12]。考虑了线路分布参数特性的分布参数模型进一步可以划分为贝杰龙模型^[13-14]和频变模型。频变模型根据频域到时域变换中所使用矩阵的不同，分为相域频变模型和模域频变模型。模域频变模型采用常数变换矩阵，只适用于平衡的传输线^[15-17]；相域频变模型采用频变变换矩阵，考虑了所有频率下线路参数的变化，是更为精确的模型^[18]。频变模型能够同时表示线路参数的分布特性及频率相关性，但其需要极为详细的输电线路结构和参数，同时在建模过程中需要对线路参数进行拟合，并引入卷积计算，在实际工程中往往难以建立该模型。文献[19]提出一种考虑特定高频频率下线路参数的贝杰龙模型，该模型与频变模型具有相同的结构与多谐振频率特性，可以对柔直系统高频谐振进行复现分析，但该方式通过线路参数变化的一般规律对高频参数进行预估，会影响仿真结果的准确性。

本文首先针对工程上广泛使用的电缆结构，总结出不同频段下电缆电气参数的简化计算方法；其次，在贝杰龙模型的基础上，考虑传输线正负零序参数的频率相关性，提出一种便于建模且考虑参数频变特性的多相电力电缆模型；最后，在PSCAD/EMTDC中通过时域仿真验证所提出的电力电缆改进贝杰龙模型的正确性和有效性。

1.   电力电缆谐波频段电气参数计算

本节根据工程中常用的电力电缆结构及其铺设方式，介绍电力电缆串联阻抗矩阵中各参数以及并联导纳的计算方法，由此推导得出电力电缆建模过程中所需的相关电气参数。

1.1   电力电缆串联阻抗矩阵Z的计算

目前工程上应用最广泛的电缆结构为单芯电缆和三芯电缆，在传输线模型建立过程中主要关注电力电缆的相关电气参数，而其主要与电缆的结构及铺设方式有关，本节以单芯电缆为例，介绍电力电缆谐波频段电气参数的计算方法。图 1、2分别为带有铠装层的单芯电缆的横、纵截面图。

图  1  单芯电缆横截面图

Figure  1.  Cross section diagram of single-core cable

下载: 全尺寸图片 幻灯片

图  2  单芯电缆纵截面图

Figure  2.  Longitudinal section diagram of single-core cable

下载: 全尺寸图片 幻灯片

计算电力电缆中各部分阻抗的方法主要分为基于贝塞尔函数的计算方法^[20]以及等效解析近似解法^[21]，本节使用基于贝塞尔函数的计算方法，主要原因在于其可以描述导体阻抗的理论特性，计算结果更精确。

图 1所示的电缆横截面图对详细的电缆材料与结构进行了简化，适用于电缆谐波频段内的电气参数计算。其中：r_ic、r_oc为线芯层的内外半径；r_is、r_os为护套层的内外半径；r_ia、r_oa为铠装层的内外半径；r_out为埋地(或海底)导体的外半径。

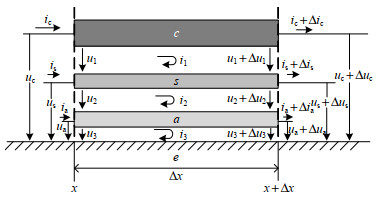
图 2为单芯电缆的纵截面图，可将单芯电缆系统看成3个回路，回路电流为I₁、I₂、I₃，回路电压为U₁、U₂、U₃^[20]。在频域内，沿电缆轴向的回路压降的方程具体可以表示为

式中：Z₁₁、Z₂₂、Z₃₃分别为回路1、2、3单位长度的自阻抗；Z₁₂、Z₂₁分别为由于1、2回路共用护套层所出现的两回路之间的互阻抗；Z₂₃、Z₃₂分别为由于2、3回路共用铠装层所出现的互阻抗。

上述自阻抗可以表示为

式中：Z_oc、Z_os、Z_oa分别为各管状导体外表面的内阻抗；Z'_cs、Z'_sa、Z'_ag分别为各绝缘介质中时变磁通表现出的阻抗；Z_is、Z_ia、Z_g分别为护套层、铠装层内表面以及大地回路的内阻抗。

上述互阻抗可以表示为

式中Z_m1、Z_m2分别为护套层、铠装层的转移阻抗。

上述各阻抗可归结为4种类型，它们的计算公式具有相同的计算形式，具体如下：

1）同心圆柱电极之间的绝缘介质中，时变磁通所表现的阻抗Z'_cs、Z'_sa、Z'_ag的计算公式为

式中：μ₀为介质的磁导率；r_o、r_i分别为该绝缘层的外径和内径；ω为电流的角频率。

2）管状导体内外表面阻抗Z_oc、Z_os、Z_oa、Z_is、Z_ia的计算公式。

外表面阻抗：

内表面阻抗：

式中：I₀、K₀、I₁和K₁分别为零阶和一阶第一类和第二类贝塞尔函数；r_ik、r_ok分别代表管状导体层k的内径与外径；ρ_k为管状导体层k的电阻率；μ_k代表管状导体层k的磁导率。式中m_k和D_k由下式计算：

需要说明的是，若线芯层为实心导体，则其内阻抗的计算公式为

3）管状导体内外表面之间的转移阻抗Z_m1、Z_m2：

4）大地回路的内阻抗Z_g。

本文利用文献[22]给出的简化公式对大地返回电阻进行计算，计算公式如下：

式中h为埋地深度。

至此，式(1)中的各部分阻抗参数均可通过相关公式进行计算，但式中的U和I是指电缆回路中的压降和电流，需修正为以大地作为参考点的回路压降和导体层实际通过的电流。通过电压和电流的关系，最后可得单相单芯电缆的阻抗矩阵Z_ph与电压电流的关系：

1.2   电力电缆并联导纳的计算

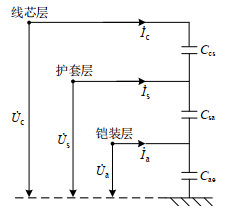
电力电缆并联导纳矩阵Y由线芯层、护套层、铠装层之间的电容构成，图 3表示电缆各层之间的电容分布。在工程中电缆的护套层和铠装层一般都是接地的，因而单芯电缆每相的对地电容都为线芯层与护套层间的电容。又由单芯电缆各相之间是相互独立的，所以正负零各序电容都等于单相电容。

图  3  单芯电缆电容分布图

Figure  3.  Capacitance distribution diagram of single-core cable

下载: 全尺寸图片 幻灯片

根据工程中电缆的结构以及铺设方式，线芯层与护套层间每相电容可由下式求得：

式中：ε_cs为电缆线芯层与护套层之间绝缘层的相对介电常数；ε₀为绝对介电常数，一般取8.85 pF/m。

1.3   电缆模型所需正负零序参数的计算

工程中常见的三相单芯电力电缆三相的铺设通常拉开一定的距离，同时各相电缆的护套层和铠装层总是接地的，即有$\Delta {\dot U_{\text{s}}} = \Delta {\dot U_{\text{a}}} = 0$，因此可以不考虑三相电缆之间的电气耦合。由此可知三序阻抗是相等的，所以单芯电缆的阻抗可由式(14)、(15)推导：

由$\Delta {\dot U_{{\text{sa}}}} = 0$，消去${\dot I_{{\text{sa}}}}$后可得：

式中Z_A为单芯电缆单相串联阻抗，电缆单位长度的正负零序串联阻抗和并联导纳是传输线建模过程中所需的相关参数。

2.   多相传输线的改进贝杰龙模型

本节在单相贝杰龙模型的基础上，介绍多导体系统中的相模变换过程，最终得到适用于时域仿真的多相贝杰龙模型。

2.1   分布参数模型

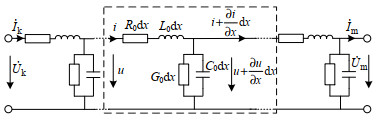
目前，传输线的建模方式主要分为集总参数模型和分布参数模型。当架空线路或电缆过长时一般采用考虑传输线分布参数特性的分布参数模型，其主要思路是认为传输线是由许多无穷小的包含电阻、电抗、电导和电纳的微元组成，如图 4所示，图中虚线框内代表一个微元。

图  4  传输线分布参数模型

Figure  4.  Distributed model of transmission line

下载: 全尺寸图片 幻灯片

一般线路的绝缘良好，可以忽略并联电导，由此可以建立输电线路的传输方程^[23-24]，根据传输线模型中相应的边界条件可对传输方程进行求解，得到首末两端电气参数在频域中的关系为

式中：$\gamma (\omega ) = \sqrt {{Z_0}(\omega ){Y_0}(\omega )}$为传输线的传播系数；${Z_{\text{c}}}(\omega ) = \sqrt {{Z_0}(\omega )/{Y_0}(\omega )}$为传输线的特性阻抗；l为传输线的长度；${\dot U_{\text{k}}}$、${\dot I_{\text{k}}}$、${\dot U_{\text{m}}}$、${\dot I_{\text{m}}}$分别为传输线的首端电压、电流和末端电压、电流；传输线的传播系数与特性阻抗的计算中有Z₀(ω) = R₀(ω) + jω L₀(ω)，Y₀(ω) = jω C₀(ω)。

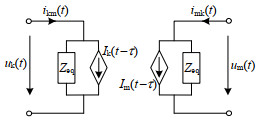
分布参数模型可进一步划分为贝杰龙模型和频变模型等，由于电磁暂态仿真通常在时域中进行，所以在建立分布参数模型时需将传输线首末端电压、电流在频域中的关系转换到时域中，最终可得到分布参数模型的等值电路，如图 5所示。

图  5  分布参数模型的等值电路

Figure  5.  Equivalent circuit of distributed model

下载: 全尺寸图片 幻灯片

单相传输线的分布参数模型均可由该等值电路表示，传输线的首末两端各接一个等值阻抗并联历史电流源的对地支路，首末两端在拓扑结构上相互独立，通过历史电流源实现首末两端间的电磁联系。

传统贝杰龙模型未考虑线路损耗以及线路参数的频率相关性，可根据行波法建立无损传输线的贝杰龙模型，无损贝杰龙模型的等值电路具有与图 5相同的结构，无损贝杰龙模型的等值电路所对应的等值阻抗和历史电流源为

式中：${Z'_0} = \sqrt {{{L}^{'}_0}/{{C}^{'}_0}}$，代表无损线路在基频下的特性阻抗；L₀^'、C₀^'分别为基频下传输线单位长度的电感和电容。

2.2   考虑线损的贝杰龙模型

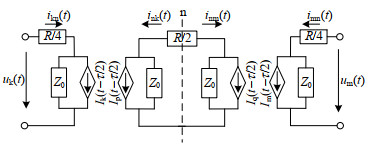
将线路的集总电阻R分成R/4、R/2、R/4分别插入传统贝杰龙模型，以此考虑传输线的线路损耗，其等值电路如图 6所示^[14]。

图  6  考虑线路损耗的贝杰龙模型的等值电路

Figure  6.  Equivalent circuit of Bergeron model considering line losses

下载: 全尺寸图片 幻灯片

通过消去中间节点可将图 6所示的模型聚合为图 5所示的模型，最终考虑线路损耗的贝杰龙模型的等值电路仍可以由图 5表示，但是等值阻抗和历史电流源的参数需进行相应的修正，由此有：

式中：Z为传输线模型等值电路中的等值阻抗；L₀、C₀分别为传输线单位长度的电感和电容；R为传输线的集总电阻。

根据上述方法可以得到考虑线损的单相贝杰龙模型，但是在实际工程中，线路通常由多根导体组成，所以需要考虑各相导线间的电磁耦合，由此建立多相传输线的模型。

2.3   多相传输线的改进贝杰龙模型

在多导体系统中，将各导体的电压、电流等物理量统称为相量。为了消去线路间的电磁耦合关系，可将相量u和i通过相模变换后变换成模量^[25]。最终，n个模量线路的计算公式可归纳为

式中：${Z_{{\text{mi}}}} = \sqrt {{L_{{\text{mi}}}}/{C_{{\text{mi}}}}}$为各模量的波阻抗；${\tau _{{\text{mi}}}} = l\sqrt {{L_{{\text{mi}}}}{C_{{\text{mi}}}}}$为各模量的传播时间。其中历史电流源需通过模域中的电压、电流的相应值进行更新。

下述为电压电流由相量转换为模量的过程：

式中：[T_e]为模量电压到相量电压的变换矩阵；[T_i]为模量电流到相量电流的变换矩阵。对于两相传输线来说，有[T_e] = [T_i]，该相模变换过程可将相互耦合的两极解耦成相互独立的0-1模分量。对于三相对称传输线来说，电压电流由相量转换为模量的过程即为克拉克变换的过程。

通过对n根多导体系统中电压、电流相量进行相模变换，可以得到模量u_m和i_m。在模域中，模量描述的偏微分方程中各分量相互独立，对模量中的各分量可以利用单相贝杰龙模型建立模量的计算公式，最终将n个模量的计算公式转换为相量形式，根据相模变换关系可得相量等值计算公式为

式中：G_p = T_i Z_m⁻¹T_e⁻¹为等值电导矩阵；I_k、I_m为等值电流源。

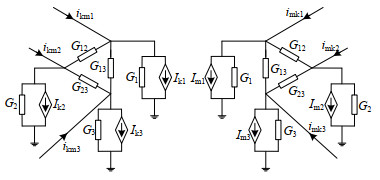
根据式(20)可得，在相量上多相传输线同样可以由等值电导和历史电流源组成的等值电路表示。三相传输线的等值电路如图 7所示，图中等值电导的电导值可以通过等值电导矩阵G_p中各元素求得，历史电流源的更新值仅与模量中的电压、电流值有关，通过相模变换后得出相量上等值电路中历史电流源的更新方式。

图  7  相域中三相传输线的等值电路

Figure  7.  Equivalent circuit of three-phase transmission line in phase domain

下载: 全尺寸图片 幻灯片

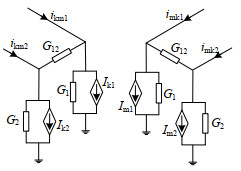
同理，对于两相传输线，也可根据相应的相模变换方式对其等值电路进行推导，推导过程与三相传输线类似，仅需使用不同于三相传输线的相模变换矩阵即可^[26]，最终推导得出的等值电路如图 8所示。

图  8  相域中两相传输线的等值电路

Figure  8.  Equivalent circuit of two-phase transmission line in phase domain

下载: 全尺寸图片 幻灯片

3.   仿真分析和实验验证

3.1节验证电力电缆谐波频段电气参数简化计算方法的正确性，并对建模过程中所需的相关中间参数进行对比，3.2节在此基础上验证电力电缆改进贝杰龙模型的准确性和有效性。

3.1   电缆参数计算方法验证

以镇海—舟山500 kV海缆工程中拟采用的国产XLPE绝缘光电复合海底电力电缆为例，对其电气参数进行计算^[7]。取海水电阻率为典型值0.5 Ω⋅m。表 1为500 kV海底电缆谐波频段电气参数计算所需的结构尺寸。为验证本文算法的准确性，采用电磁暂态仿真软件PSCAD/EMTDC进行对比。以上述电缆为对象，将本文算法得出的结果与PSCAD/ EMTDC中的计算结果进行对比，PSCAD/EMTDC中计算得出的电缆电气参数可从输出的中间结果查看，本文算法与PSCAD的对比结果如表 2、3所示。

表  1  500kV交联聚乙烯绝缘海底电缆的结构尺寸

Table  1.  Sizes of 500kV XLPE submarine cable

分类	电缆结构	参数
导体	材料	铜
	导体直径/mm	51.5
XLPE绝缘	绝缘厚度/mm	31
	绝缘外径/mm	117.98
护套	材料	铅
	护套层厚度/mm	4.5
	护套层外径/mm	133.98
PE外护层	外护层厚度/mm	4
	外护层外径/mm	141.98
铠装	材料	钢
	铠装层厚度/mm	3.5
	铠装层外径/mm	161.98

下载: 导出CSV 

| 显示表格

表  2  单芯电缆电气参数不同算法间结果对比

Table  2.  Calculation results comparison between electrical parameters of single-core cables

频率/kHz	正、零序电阻/(Ω/m)			正、零序电感/(mH/m)
	本文算法	PSCAD		本文算法	PSCAD
0.05	68.8	68.8		251.9	253.6
0.50	110.9	111.4		203.3	203.2
1.00	149.9	150.4		196.1	196.0
1.50	177.6	178.1		192.2	192.1
2.00	197.6	198.1		189.9	189.8
2.50	213.5	214.0		188.5	188.5
3.00	227.2	227.7		187.5	187.5
3.50	239.8	240.4		186.8	186.8
4.00	251.8	252.3		186.3	186.3
4.50	263.4	264.0		185.9	185.9
5.00	274.6	275.1		185.5	185.5

下载: 导出CSV 

| 显示表格

表  3  单芯电缆波阻抗不同算法间结果对比

Table  3.  Calculation results comparison between intermediate parameters of single-core cables

频率/kHz	阻抗/Ω
	本文算法	PSCAD
0.05	41.78	41.82
0.50	37.53	37.53
1.00	36.86	36.86
1.50	36.50	36.49
2.00	36.28	36.27
2.50	36.14	36.14
3.00	36.05	36.05
3.50	35.98	35.98
4.00	35.93	35.93
4.50	35.89	35.89
5.00	35.85	35.86

下载: 导出CSV 

| 显示表格

根据表 2、3的对比结果可知，本文简化算法得出的结果与PSCAD中计算得出的结果在谐波频段内基本相同。同时，对于三相单芯带铠装电缆来说，本文在计算过程中生成的矩阵阶数相较于PSCAD中生成的矩阵阶数大大减小，可以很好地节省参数计算所使用的计算资源。

在传输线模型建立的过程中，最终等值电路中电导的数值和等值电流源的更新与各序计算得出的电气参数有关，根据上述计算得出的各序电阻、电感参数，计算各序的波阻抗，以此验证本文算法对谐波频段内等值电路中所需参数计算的准确性，对比结果如表 3所示。

以2 kHz为例，对比提出的简化算法与PSCAD/EMTDC中计算结果之间的相对误差，在该频率下，简化算法计算得出的正、零序电阻的相对误差为0.25%，正、零序电感的相对误差为0.05%。电缆建模过程中所需的波阻抗的相对误差为0.03%，表 3中各频率下波阻抗的最大误差仅为0.1%。根据对比结果可知，在高频情况下，电力电缆的正、零序电感参数基本维持恒定，同时由于正、零序电容参数不随频率的改变而改变，所以与电力电缆建模相关的波阻抗、传播时间随频率的升高变化不大。当需要对有高频谐振发生的工况进行仿真时，可以根据本文总结的简化算法对电力电缆模型中的电气参数进行修正，以此反映电缆电气参数的频率相关性。

3.2   模型测试

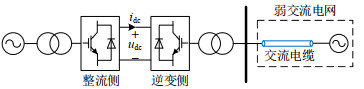
以典型背靠背柔直系统为例，当逆变侧交流电网中大部分线路相继断开，仅有一条线路未断开时，逆变侧电网近似为弱交流电网^[27]，此时会出现高频谐振现象。仿真系统的局部结构图如图 9所示，送端采用有功功率控制和定无功功率控制，受端采用定直流电压控制和定交流电压控制。

图  9  产生谐波时柔直系统的局部结构图

Figure  9.  Local structure diagram of VSC-HVDC system

下载: 全尺寸图片 幻灯片

为验证本文所提出的模型适用于电力系统产生宽频谐波时的分析，分别对比电力电缆在不同建模方式下的仿真结果，以此验证所提出模型的有效性和准确性。设置逆变侧交流母线在2.1 s时发生持续时间为0.05 s的C相接地故障。

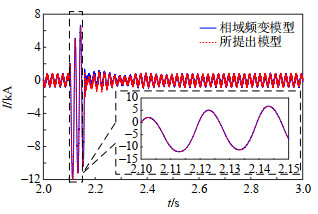
图 10为电力电缆的建模方式分别为频变模型以及本文所提模型时，逆变侧变压器网侧电流的仿真结果。其中频变模型采用PSCAD/EMTDC中的相域频变模型，其考虑了所有频率下线路参数的变化情况，后文仿真中所使用的频变模型均为相域频变模型。

图  10  不同模型下逆变侧变压器网侧电流的对比结果

Figure  10.  Simulation results of current using different model

下载: 全尺寸图片 幻灯片

图 11对两种建模方式下故障相电流波形进行对比分析。根据图 11中对故障相电流波形的对比结果可知，所提出模型与频变模型的电流波形在稳态、暂态过程中吻合程度良好，暂态过程中波峰处的相对误差分别为2.45%、1.17%、1.67%。

图  11  故障相电流波形的对比结果

Figure  11.  Comparison of fault current waveforms

下载: 全尺寸图片 幻灯片

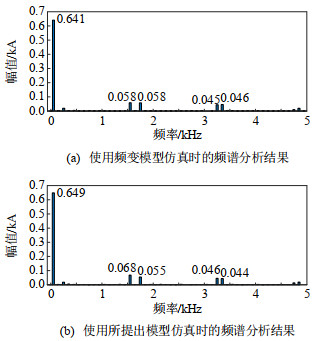
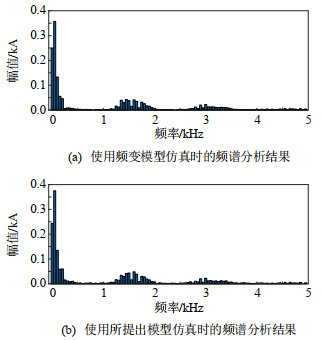
图 12、13分别对故障发生前的稳态过程、故障发生后的暂态过程中A相电流波形进行频谱分析。

图  12  稳态过程中电流波形的频谱分析对比结果

Figure  12.  Comparison of spectrum analysis results in steady-state process

下载: 全尺寸图片 幻灯片

图  13  暂态过程中电流波形的频谱分析对比结果

Figure  13.  Comparison of spectrum analysis results in transient process

下载: 全尺寸图片 幻灯片

根据图 12、13的频谱分析结果可以得出，提出模型与频变模型均可反映系统在稳态、暂态过程中的各次谐波分量。在故障发生前的稳态过程中，使用两种模型仿真时电流中谐波含量较高的谐波频率分别为1.55、1.75、3.25、3.35 kHz，其对应的幅值在图 12中进行了相应的注明。暂态过程中电流的频谱分析结果如图 13所示，根据频谱分析的对比结果，所提出模型同样可以较好地反映暂态过程中的各次谐波分量。

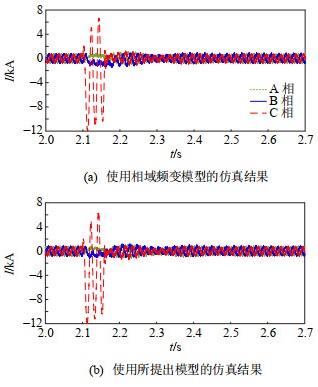
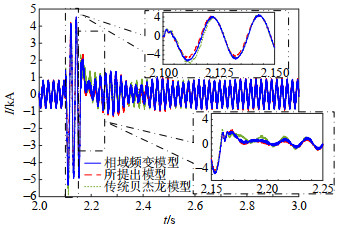
同时，将单相短路故障的位置设置至逆变侧交流电网出口处，模拟极端短路故障的情况。为验证利用谐波频率修正电缆电气参数来改进贝杰龙模型的必要性，在系统中电力电缆的建模方式分别为频变模型、传统贝杰龙模型以及本文所提出模型的3种情况下，对比逆变侧变压器网侧电流的波形，对比结果如图 14所示。

图  14  极端故障情况下电流波形的对比结果

Figure  14.  Comparison of current waveforms under extreme fault conditions

下载: 全尺寸图片 幻灯片

对比结果显示，在故障过程中，使用本文所提出模型与使用频变模型进行仿真时波峰处的相对误差分别为1.24%、0.68%。相较于传统贝杰龙模型，提出的模型可以更好地反映暂态峰值出现的时刻，以2.122 s时刻为例，在该时刻使用频变模型和本文所提出模型仿真时的电流波形取得峰值，而传统贝杰龙模型在9个仿真步长后取得峰值。出现上述差别的主要原因在于传统贝杰龙模型未考虑电缆参数的频率相关性，而所提出模型中的相关电气参数已被修正，仿真得出的波形与使用频变模型仿真得出的波形间吻合程度更好。

图 14在故障清除后恢复至稳态的过程中，所提出的模型与频变模型的吻合程度更好，而未考虑电缆参数频变特性的传统贝杰龙模型不能正确反映故障结束后一段时间内的电流波形。对该过程中的电流波形进行频谱分析，使用相域频变模型、本文所提出模型、传统贝杰龙模型进行仿真时电流基波分量的幅值分别为467、404、827 A，传统贝杰龙模型与相域频变模型之间的误差较大。同时所提出模型可以较好地表示高频谐波分量，而传统贝杰龙模型无法正确表示3.4 kHz附近的高频谐波分量。由此表明，本文所提出的模型考虑了电力电缆的分布参数特性以及电气参数的频率相关性，可以较好地反映系统中的谐波分量，暂态、稳态过程的仿真波形与使用频变模型得出的仿真波形间吻合程度良好。

4.   结论

本文对电力电缆在谐波频段内的建模方法展开了研究，将电力电缆建模过程中电缆电气参数计算以及模型建立这两个部分联系起来，提出一种考虑参数频变特性的电力电缆改进贝杰龙模型。主要结论如下：

1）基于电缆的结构以及铺设方式，提出一种电力电缆谐波频段电气参数的简化计算方法，相关电气参数的计算结果与PSCAD/EMTDC中计算得出的结果间的相对误差在各频率下均在1%以内，同时根据计算结果发现在高频下电力电缆模型所需的相关参数随频率的变化不大，可为谐波频段内电力电缆模型中相关参数的选择提供一定的参考；

2）考虑到频变模型在建模过程中需进行卷积计算、参数拟合等过程，在实际工程中难以建立，由此在原有贝杰龙模型的基础上，提出一种考虑线路频变特性的电力电缆模型，使用该模型进行仿真能较为准确地反映电网中出现的谐波，且该模型的建模过程简单、仿真效率较高。