Influence of Supply Voltage Flicker on Rotor Fault Online Detection of Induction Motors and Countermeasures
-
摘要: 供电电压闪变可能对异步电动机转子故障在线检测产生不利影响，导致基于定子电流信号分析(motor current signature analysis，MCSA)的转子故障在线检测方法失效。通过理论分析，揭示供电电压闪变恶化转子故障在线检测性能的机制。提出免于供电电压闪变影响的异步电动机转子故障在线检测方法，首先，根据转子故障主特征频率分量预判转子健康或故障；继而，根据转子故障独有的辅助特征频率分量进一步确认转子健康或故障。仿真与实验结果证明了该方法的有效性。Abstract: Supply voltage flicker might adversely influence the rotor fault online detection of induction motors, making the motor current signature analysis (MCSA) based detection method ineffective. Through theoretical analysis, this paper reveals the mechanism that supply voltage flicker exacerbates the performance of rotor fault online detection. We present an online rotor fault detection method that is immune to supply voltage flicker. This method comprises two main steps: first, a preliminary judgment of the rotor's health or fault status is made based on the primary characteristic components of rotor faults; second, the preliminary judgment is further verified using auxiliary components that are uniquely associated with rotor faults. Simulation and experimental results demonstrate the effectiveness of the presented method.
-
Keywords:
- induction motor /
- rotor fault /
- broken rotor bar /
- supply voltage flicker /
- online detection
-
0. 引言
异步电动机转子故障是指其转子导条或端环断裂故障，该故障将导致电机出力下降，甚至严重的“扫膛”而损伤定子铁心和绝缘。该故障的发生概率达10%左右[1-2]，因此必须对其进行检测。
迄今，异步电动机转子故障在线检测研究已经取得长足进展[1-2]。异步电动机转子故障在线检测的理论基础在于：一旦发生转子故障，则在定子电流信号中出现某些特定的频率分量，通常将其称为转子故障特征分量。因此，通过对定子电流信号进行频谱分析并提取、考察该特征分量，即可实现转子故障检测。这就是基于定子电流信号分析(motor current signature analysis，MCSA)的转子故障检测方法。转子故障特征分量的频率通常接近于供电频率(基波)，转子故障特征分量因而容易受到基波分量的影响；加之转子故障特征分量的幅值一般远小于基波分量，在某些不利情况下甚至被后者完全淹没，MCSA方法将可能失效。因此，为了保证转子故障在线检测的性能，必须应用高性能的信号处理技术并采取诸多措施，以凸显转子故障特征分量。
李睿彧等人应用变分模态分解，实现了定子电流的基波和谐波分量的分解，并结合Park变换，避免了定子电流基波分量泄漏对转子故障特征分量的影响[3]。Li Haiyang等人提出了一种归一化的频域能量算子，以之处理定子电流信号，从而避免定子电流基波分量泄漏的影响[4]。与之类似，Wang Wanding等人引入三阶能量算子，以遏制定子电流基波分量的泄漏，并凸显转子故障特征[5]。Gholam Reza A等人将离散小波变换和Teager-Kaiser算子相结合，以保证转子故障在线检测的准确性[6]。
在上述方法中，被分析信号(通常称为分析媒介)均是电机稳态运行时的定子电流信号，文献[7-9]则通过分析电机启动过程中的暂态性质的定子电流信号进行转子故障在线检测。
除定子电流信号外，电机的其他一些信号也可作为分析媒介而用于转子故障在线检测。谢颖等人研究了转子正常和故障情况下的定转子电流、气隙磁密等的变化趋势及其与故障程度的关联性，为分析媒介的多角度选择提供了有益参考[10]。分析媒介的恰当选择，可以达成改进转子故障在线检测性能的目的。许伯强等人选择无功和有功功率信号作为分析媒介[11]，Park Y等人以定子电流空间矢量作为分析媒介[12]，Spyropoulos D V等人采用转矩信号作为分析媒介[13]，文献[14-16]采用杂散或气隙磁通作为分析媒介，均实现了对转子故障在线检测方法的改进。
异步电动机转子故障在线检测方法研究虽已取得长足进展，但仍有待完善。事实上，在转子故障在线检测实践中，经常有“误判”发生。文献[7, 14-16]指出，转子轴向风道将引发磁场的不对称，这与转子故障的磁效应类似，因此可能导致MCSA方法“误判”。为此，文献[7, 4-16]分别以启动过程中的暂态定子电流信号、杂散或气隙磁通作为分析媒介，提出了免于轴向风道影响的应对方案。文献[11]指出，以近似于两倍转差频率波动的负荷将在定子电流中产生某些频率的特定分量，这一效果类似于转子故障，从而导致MCSA方法“误判”。为此，文献[11]以无功和有功功率信号作为分析媒介，提出了免于负荷波动影响的应对方案。另外，Park Y等人发现，当电机拖动泵、风扇、压缩机等机械设备时，如果电机的磁极数等于机械设备叶片数的整数倍，则叶片通频振动将在定子电流中产生某些频率的特定分量，这一效果与转子故障类似，从而导致MCSA方法“误判”[12]。为此，Park Y等人以定子电流空间矢量作为分析媒介，提出了免于叶片通频振动影响的应对方案[12]。
对于重要工位的大型异步电动机而言，“误判”是需要付出巨大代价的。假如将轴向风道、负荷波动、叶片通频振动等现象“误判”为转子故障，现场技术人员为了确保安全生产即可能将电机停机、解体以检修转子，这将导致无谓的维修成本和高昂的停产损失。因此，在转子故障在线检测实践中，必须竭尽所能地避免“误判”。
综上，影响转子故障在线检测性能的因素可以总结、归类为：信号处理技术的性能；分析媒介的性能；转子的本体结构，如轴向风道；负荷特性，如负荷波动或缺陷、叶片通频振动。对于上述影响，目前均已提出相应的应对方案。
此外，异步电动机是在供电电压的激励下运行的。与上述因素类似，供电电压质量也可能对转子故障在线检测产生不利影响。1994年，国际电工委员会将电压闪变列为衡量电能质量的重要指标之一。自此，电压闪变问题获得了持续关注[17-19]。近年来，风电、光伏等可再生能源大规模接入电网，其固有的波动性加剧了电压闪变问题[19]。
类似于轴向风道、负荷波动、叶片通频振动等因素，供电电压闪变也可能导致MCSA方法“误判”。因此，研究供电电压闪变对转子故障在线检测的影响并提出应对方案，有其必要性。
1. 转子故障在线检测的理论基础
异步电动机转子故障将导致其定子电流中出现式(1)所确定频率的特定分量[1-2]。不妨称之为转子故障主特征分量，对应的频率称为转子故障主特征频率，即
$$ (1 \pm 2s){f_{\text{1}}}\; $$ (1) 式中：s表示转差率；f1表示供电频率，即基波频率。
因此，通过对定子电流信号进行频谱分析并提取、考察该分量，即可实现转子故障在线检测[1-2]。
转子故障也将导致定子电流中出现式(2)、(3)所确定频率的特定分量[1-2]。不妨称之为转子故障辅助特征分量，对应的频率称为转子故障辅助特征频率。但是，转子故障辅助特征分量在幅值上显著小于转子故障主特征分量，因此在转子故障检测实践中并未被关注。
$$ (1 \pm 4s){f_{\text{1}}}\; $$ (2) $$ [k(1 - s) \pm s]{f_{\text{1}}}\;, \;k = \;3, \;5, \;7, \; \cdots $$ (3) 2. 供电电压闪变影响转子故障在线检测
2.1 供电电压闪变的数学模型
供电电压闪变可以视为一调幅波电压对供电电压基波分量的调制，以A相电压为例，其数学模型定义[17-19]为
$$ \begin{array}{l} {u_{\text{s}}}(t) = [{A_1} + {A_{\text{m}}}\cos (2\pi {f_{\text{m}}}t + {\phi _{\text{m}}})]\cos (2\pi {f_1}t) = \hfill \\ \;\;\;{A_1}\cos (2\pi {f_1}t) + \frac{{{A_{\text{m}}}}}{2}\cos [2\pi ({f_1} + {f_{\text{m}}})t + {\phi _{\text{m}}}] + \hfill \\ \;\;\;\frac{{{A_{\text{m}}}}}{2}\cos [2\pi ({f_1} - {f_{\text{m}}})t - {\phi _{\text{m}}}] \hfill \\ \end{array} $$ (4) 式中：A1表示基波分量的幅值；Am、fm、ϕm分别表示调幅波电压的幅值、频率和初相角；t表示时间。
根据国标GB/T12326—2008《电能质量电压波动和闪变》可知，调幅波电压的幅值远小于供电电压基波分量。譬如，对于标称电压等级在1 kV以下的供电系统，其电压波动限值$ d = 2\sqrt 2 {A_\text{m} }{\text{/}}{A_1} $不得超过4%，因此Am/A1 < 1.4%。另外，调幅波电压的频率fm介于0.05~35 Hz。
2.2 供电电压闪变影响转子故障在线检测的机制
假定转子正常，而供电电压存在式(4)所示的相对于基波分量的闪变。忽略电机饱和等非线性因素，则供电电压可以近似视为基波分量与(f1±fm)分量的叠加。将供电电压的(f1±fm)分量称为供电电压闪变分量，并推导其所导致的定子电流分量的频率表达式[20]。
对于供电电压的(f1+fm)分量，在其作用下，三相定子绕组中将流过对称的(f1+fm)频率的电流分量，并产生旋转磁场：
$$ {B_{\text{s}}}(\theta , \;t) = \sum\limits_\nu {{B_{{\text{s}}\nu }}\cos ({\omega _ + }t - \nu \theta )} $$ (5) 式中：ν=6c+1表示定子磁场的谐波次数；c=0, ±1, ±2, ⋯；Bsν=$ 3\sqrt 2 {\mu _0}N{k_{{\text{w}\nu }}}{I_{\text{s}}}/({\text{π }}\nu P\delta ) $；μ0表示真空磁导率；N表示一相绕组串联匝数；kwν表示ν次谐波绕组因数；Is表示定子电流有效值；P表示极对数；δ表示气隙长度；ω+=2π(f1+fm)；θ表示定子坐标系下的空间电弧度，用以描述定子内圆表面各点的空间位置。
设n为转子转速，n+为定子基波磁场的转速，则对应的转差率为
$$ {s_ + } = \frac{{{n_ + } - n}}{{{n_ + }}} = \frac{{[60({f_1} + {f_{\text{m}}})]{\text{/}}P - (1 - s)60{f_1}{\text{/}}P}}{{[60({f_1} + {f_{\text{m}}})]{\text{/}}P}} $$ (6) 即：
$$ {s_ + } = \frac{{s{f_1} + {f_{\text{m}}}}}{{{f_1} + {f_{\text{m}}}}} $$ (7) 设α为转子坐标系下的空间电弧度，则θ可以表示为θ=α+(1−s+)ω+t。将其代入式(5)，可以得到定子磁场在转子坐标系下的表达式：
$$ {B_{\text{s}}}(\alpha , \;t) = \sum\limits_\nu {{B_{{\text{s}\mathtt{ν}}}}\cos \{ [1 - \nu (1 - {s_ + })]{\omega _ + }t - \nu \alpha \} } $$ (8) 根据式(8)可知，定子磁场在转子中感应电动势的频率为[1−ν(1−s+)](f1+fm)，对应产生同频率的转子电流，继而产生转子磁场：
$$ {B_{\text{r}}}(\alpha , \;t) = \sum\limits_\nu {\sum\limits_m {{B_{{\text{r}}\nu m}}\cos \{ [1 - \nu (1 - {s_ + })]{\omega _ + }t - m\alpha \} } } $$ (9) 式中：m=k(Z2/P)±1表示转子磁场的谐波次数，k=0, 1, 2, …, Z2表示转子槽数；Brνm$ = \sqrt 2 {\mu _0}{Z_2}\sin (\pi mP{\text{/}}{Z_2}) \cdot $$ {I_{\text{r}}}{\text{/}}(\pi mP\delta ) $；Ir表示转子电流有效值。
将式(9)转换至定子坐标系，可得：
$$ {B_{\text{r}}}(\theta , \;t) = \sum\limits_\nu {\sum\limits_m {{B_{{\text{r}}\nu m}}} } \cos \{ [1 + (m - \nu )(1 - {s_ + })]{\omega _ + }t - m\theta \} $$ (10) 式(10)即为源于供电电压(f1+fm)闪变分量、计及转子调制效应的转子磁场的解析表达式。需要注意，式(10)是以定子坐标系为参照的。因此，转子磁场在定子绕组中产生的感应电动势、电流的频率即为其自身的频率，即
$$ [1 + (m - \nu )(1 - {s_ + })]({f_1} + {f_\text{m} }) $$ (11) 类似地，对于供电电压的(f1−fm)分量，其引发的转子磁场在定子绕组中产生的感应电动势、电流的频率为
$$ [1 + (m - \nu )(1 - {s_ - })]({f_1} - {f_\text{m} }) $$ (12) 其中：
$$ {s_ - } = \frac{{s{f_1} - {f_{\text{m}}}}}{{{f_1} - {f_{\text{m}}}}} $$ (13) 这表明，供电电压闪变分量将导致定子电流中出现式(11)、(12)所确定频率的特定分量。不妨称之为供电电压闪变特征分量，对应的频率称为供电电压闪变特征频率。
根据式(11)、(12)可知，供电电压闪变特征频率的取值非常复杂，涉及m、ν、s以及fm间的取值组合，为清楚起见，一并示于式(14)。仅就基波而言(m=1、ν=1)，闪变特征频率为f1±fm，亦即定子电流中包含f1±fm频率的闪变特征分量。
$$ \left\{ \begin{array}{l} m = k({Z_2}/P) \pm 1, \;\;k = 0, \;1, \;2, \; \cdots \hfill \\ \nu = 6c + 1, \;\;c = 0, \; \pm 1, \; \pm 2, \; \cdots \hfill \\ s \in [\begin{array}{*{20}{c}} {0.002}&{0.05} \end{array}] \hfill \\ {f_{\text{m}}} \in [\begin{array}{*{20}{c}} {0.05}&{35} \end{array}]{\text{Hz}} \hfill \\ \end{array} \right. $$ (14) 根据式(1)可知，转子故障主特征分量的频率为f1±2sf1。通常异步电动机运行时，s介于0.002~0.05之间，则2sf1介于0.2~5 Hz(取f1=50 Hz)。如前所述，fm介于0.05~35 Hz(参见国标GB/T12326—2008)。自然，fm是可能等于2sf1的。此时，供电电压闪变特征分量——f1±fm频率分量，即可能混淆转子故障主特征分量——f1±2sf1频率分量，从而影响转子故障在线检测，导致MCSA方法“误判”——将供电电压闪变错误地判断为转子故障。
对于选择无功和有功功率信号[11]、定子电流空间矢量[12]、转矩信号[13]以及杂散或气隙磁通[14-16]作为分析媒介的转子故障在线检测方法，供电电压闪变同样可能产生不利影响。
总之，供电电压闪变对当前的转子故障在线检测方法普遍存在不利影响，亟待提出免于供电电压闪变影响的转子故障在线检测方法。
3. 免于供电电压闪变影响的转子故障在线检测
考虑到MCSA方法应用广泛，并具实用性，本文以之为基础而提出了免于供电电压闪变影响的转子故障在线检测方法。
因为旨在免于供电电压闪变的影响，需要另行采集一相供电电压信号。考虑到电压信号在工程现场易于采集，因此增加一相电压信号的采集，于工程现场是可以接受的。
3.1 基本思路
如前所述，若fm近似等于2sf1，供电电压闪变特征分量则可能混淆转子故障主特征分量，从而影响转子故障在线检测。自然，只要寻找到转子故障独有的、区别于供电电压闪变的特征频率及分量，进而考察该分量，即可克服供电电压闪变对转子故障在线检测的影响。
式(2)、(3)给出了转子故障辅助特征频率，式(11)、(12)则给出了供电电压闪变特征频率。对比可知，转子故障独有的、区别于供电电压闪变的特征频率及分量是存在的。
3.2 主要步骤
本文提出了免于供电电压闪变影响的转子故障在线检测方法，基本步骤如下。
1）采集一相电压信号us(t)、一相电流信号is(t)，采样频率为5 kHz。
2）基于定子电流信号分析，考察主特征频率分量，进行转子故障检测，并预判转子状态：健康或故障。
这就是MCSA方法。通过引入高性能的信号处理技术，MCSA方法已经发展、衍生出诸多形式，参阅文献[1, 3-6]。本文采用基于自适应滤波和细化快速傅里叶变换(fast Fourier transform，FFT) 频谱分析的MCSA方法[1]。首先，对is(t)进行细化FFT频谱分析，确定其基波分量的幅值Im和频率f1；之后，对is(t)做自适应滤波以滤除其基波分量，结果记为Δi(t)；进而，对Δi(t)进行细化FFT频谱分析，确定其(1-2s) f1频率分量的幅值ILm、(1+2s) f1频率分量的幅值IRm；最后，预判转子状态：健康或故障。
注意：转差率s可以通过考察is(t)的齿槽谐波分量确定，参阅文献[1]；具体诊断判据，亦参阅文献[1]。
3）检测供电电压闪变并判断其是否影响转子故障检测。
检测供电电压闪变的方法，不一而足[17-19]。与前述MSCA方法类似，本文采用基于自适应滤波和细化FFT频谱分析的方法。首先，根据步骤2）确定的f1，计算us(t)在f1处的细化FFT频谱，确定其基波分量的幅值A1；之后，对us(t)做自适应滤波以滤除其基波分量，结果记为Δu(t)；进而，对Δu(t)进行细化FFT频谱分析，确定供电电压闪变分量的幅值Am/2和频率fm；最后，根据fm是否接近2s f1判断供电电压闪变是否影响转子故障检测。
若供电电压闪变并不影响转子故障检测，则步骤2）对转子状态的预判成立，转子故障检测完成，异步电动机状态为正常或故障；否则，需进一步执行后续步骤。
4）确定当前转子故障独有的、区别于供电电压闪变的特征频率，记为fRF。
根据式(2)、(3)计算转子故障辅助特征频率，根据式(11)、(12)、(14)计算与其接近的供电电压闪变特征频率，并将二者对比，从而遴选出转子故障所独有的特征频率fRF。
5）检查is(t)的细化频谱图中是否存在对应的谱峰。如果在fRF处存在谱峰，则转子故障，异步电动机状态为故障，且供电电压闪变；否则，转子健康，异步电动机状态为健康，仅供电电压闪变。
4. 仿真与实验结果
针对1台Y100L-2型三相笼型异步电动机(3 kW、380 V、50 Hz、9.9 N·m、Y接、转子20根导条)进行仿真与实验以验证上述工作。
4.1 仿真结果
采用多回路模型进行仿真，关于多回路模型以及被仿真电机的详尽参数，参阅文献[1]。
4.1.1 供电电压正常情况
设定供电电压正常，即仅含基波分量、且A相电压us(t)按照式(4)规律变化，而A1=310.27 V、f1=50 Hz、Am=0 V。同时，设定负载转矩为4.95 N·m (近似半载)。
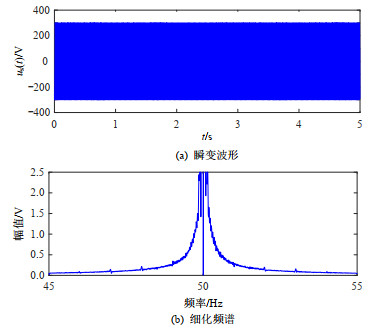
图 1(a)、(b)分别表示us(t)的瞬变波形、细化FFT频谱。
![]()
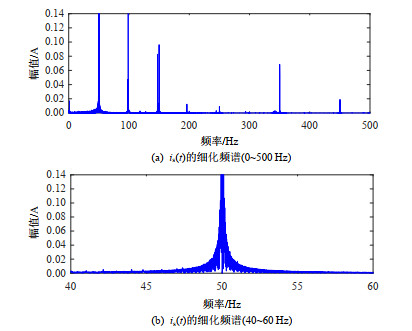
图 1 供电电压正常时A相电压的瞬变波形和细化频谱Figure 1. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is normal设定转子健康，图 2表示is(t)在0~500 Hz内的细化FFT频谱。
![]()
图 2 供电电压正常且转子健康时的仿真结果Figure 2. Simulation results while supply voltage is normal and rotor is healthy此时，f1=50 Hz、s ≈0.018 3。根据式(1)—(3)可以计算出此时的转子故障特征频率，示于表 1。
表 1 转子故障特征频率Table 1. Feature frequencies of rotor faultHz (1-2s)f1 (1+2s)f1 (1-4s)f1 (1+4s)f1 [k(1-s) ±s]f1(k=7) (7-8s)f1 (7-6s)f1 48.17 51.83 46.34 53.66 342.68 344.51 根据图 2、表 1可知，在转子故障主特征频率附近并无明显的谱峰，因此可以预判转子健康。根据图 1(b)可以判定供电电压闪变不存在。因而，可以确认转子健康。
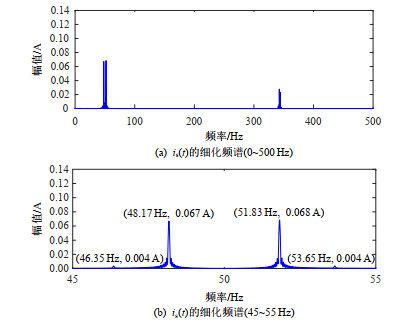
设定转子1根导条断裂，图 3(a)、(b)分别表示is(t)在0~500 Hz、45~55 Hz内的细化FFT频谱。
![]()
图 3 供电电压正常且转子故障时的仿真结果Figure 3. Simulation results while supply voltage is normal and rotor is faulty根据图 3(a)、(b)和表 1可知，在转子故障主特征频率附近出现明显的谱峰，因此可以预判转子故障，而供电电压闪变并不存在，可以确认转子故障。
4.1.2 供电电压闪变情况
设定供电电压闪变，且A相电压us(t)按照式(4)规律变化，而A1=310.27 V、f1=50 Hz、Am=0.014A1=4.34 V、fm=1.83 Hz。同时，设定负载转矩为4.95 N·m (近似半载)。注意：设定fm=1.83 Hz，是因为s ≈0.018 3、f1=50 Hz，而2s f1≈1.83 Hz，则fm与2s f1近似相等，这是供电电压闪变影响转子故障检测的最不利情况。
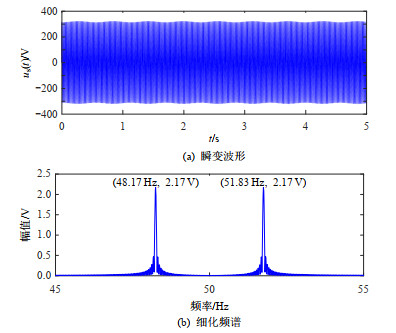
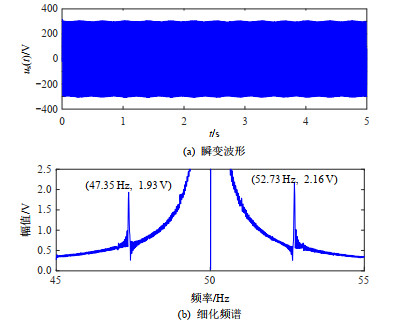
图 4(a)、(b)分别表示us(t)的瞬变波形、细化FFT频谱。
![]()
图 4 供电电压闪变时A相电压的瞬变波形和细化频谱Figure 4. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is flickering对比图 4与图 1可知，供电电压闪变使us(t)的包络出现脉动，并使其细化频谱在(f1-fm)=48.17 Hz和(f1+fm)=51.83 Hz处出现谱峰。
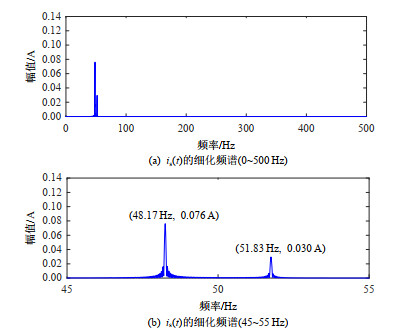
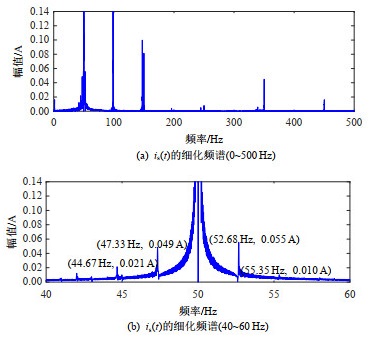
设定转子健康，仿真结果示于图 5。其中，图 5(a)、(b)分别表示is(t)在0~500 Hz、45~55 Hz内的细化FFT频谱。
![]()
图 5 供电电压闪变且转子健康时的仿真结果Figure 5. Simulation results while supply voltage is flickering and rotor is healthy根据图 5、表 1可知，在转子故障主特征频率附近出现明显的谱峰，因此现有的MCSA方法将判断：转子故障。但实际情况是转子健康，仅供电电压闪变而已。这就意味着现有的MCSA方法是受供电电压闪变影响的，因而将供电电压闪变“误判”为转子故障。
根据图 4(b)可以判定供电电压闪变存在并将影响转子故障检测。因此，需采取进一步措施予以避免。
此时，f1=50 Hz、fm=1.83 Hz。以表 1为参考，根据式(11)、(12)、(14)计算出与转子故障特征频率接近的供电电压闪变特征频率：48.17、51.83、146.34、150.00、244.51、248.17、342.68、346.34、440.85、444.51 Hz。上述频率可能混淆转子故障特征频率。对照表 1，可以确定当前转子故障独有的、区别于供电电压闪变的特征频率fRF为46.34、53.66、344.51 Hz。
根据图 5可知，is(t)的细化频谱在fRF附近并无谱峰。因此，根据本文所提方法可以进一步确认：转子健康，但供电电压闪变。自然，该判断是正确的。
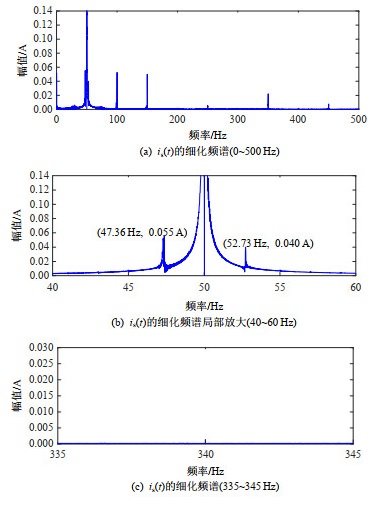
设定转子1根导条断裂，仿真结果示于图 6。其中，图 6(a)—(c)分别表示is(t)在0~500 Hz、45~55 Hz、340~350 Hz内的细化FFT频谱。
![]()
图 6 供电电压闪变且转子故障时的仿真结果Figure 6. Simulation results while supply voltage is flickering and rotor is faulty根据图 6(a)、(b)和表 1可知，在转子故障主特征频率附近出现明显的谱峰，因此预判：转子故障。根据图 4(b)可以判定供电电压闪变存在并将影响转子故障检测，因此采取进一步措施。
如前所述，可以确定当前转子故障独有的、区别于供电电压闪变的特征频率fRF为46.34、53.66、344.51 Hz。根据图 6(b)、(c)可知，is(t)的细化频谱在fRF附近出现谱峰。因此，根据本文所提方法可以进一步确认：转子故障，同时供电电压闪变。自然，该判断是正确的。
对比图 6(b)、图 3(b)可知，二者在fRF=46.34 Hz和fRF=53.66 Hz附近的谱峰几乎完全相同。这就表明，供电电压闪变对于fRF处的is(t)细化频谱无影响。因此，通过考察fRF特征频率分量以避免供电电压闪变对转子故障检测的影响，在理论上是可行的。
4.2 实验结果
实验设备如图 7所示，主要包括笼型异步电动机、直流测功机(作为可调负载)、另行配备的故障转子(模拟1根转子导条断裂)、信号采集分析装置、配电变压器(将实际的电网电压施加于电机)以及可编程交流电源(模拟闪变的供电电压)。
4.2.1 供电电压正常情况
为结合实际，通过配电变压器将实际的电网电压施加于电机。实际的电网电压无闪变，但包含谐波。设定负载转矩为9.9 N·m(近似满载)。
图 8(a)、(b)分别表示us(t)的瞬变波形、细化FFT频谱。
![]()
图 8 供电电压正常时A相电压的瞬变波形和细化频谱Figure 8. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is normal转子健康情况下，图 9(a)、(b)分别表示is(t)在0~500 Hz、40~60 Hz内的细化FFT频谱。
![]()
图 9 供电电压正常且转子健康时的实验结果Figure 9. Experimental results while supply voltage is normal and rotor is healthy对比图 9(a)、图 2可知，相对于仿真而言，实验is(t)包含谐波分量，并且其基波分量未被自适应滤波完全滤除。这说明，针对实验is(t)基波分量的自适应滤波的效果逊色于仿真情况。这是因为，实际电机is(t)的基波分量必然存在一定程度的波动，包括幅值和频率，因此自适应滤波无法将其理想滤除。
此时，f1=50.04 Hz、s≈0.027 6。根据式(1)—(3)可以计算出此时的转子故障特征频率，示于表 2。
表 2 转子故障特征频率Table 2. Feature frequencies of rotor faultHz (1−2s)f1 (1+2s)f1 (1−4s)f1 (1+4s)f1 [k(1−s)±s]f1 (k=7) (7−8s)f1 (7−6s)f1 47.28 52.80 44.52 55.56 339.23 341.99 根据图 9、表 2可知，在转子故障主特征频率附近并无明显的谱峰，因此可以预判转子健康。根据图 8(b)可以判定供电电压闪变不存在。因而，可以确认转子健康。
以故障转子替换正常转子，实验结果示于 图 10。其中，图 10(a)、(b)分别表示is(t)在0~500 Hz、40~60 Hz内的细化FFT频谱。
![]()
图 10 供电电压正常且转子故障时的实验结果Figure 10. Experimental results while supply voltage is normal and rotor is faulty根据图 10(a)、(b)和表 2可知，在转子故障主特征频率附近出现明显的谱峰，因此可以预判转子故障。根据图 8(b)可以判定供电电压闪变不存在。因而，可以确认转子故障。
4.2.2 供电电压闪变情况
测取并存储配电变压器施加于电机的三相电压信号，按照式(4)以相同采样频率叠加闪变分量，由可编程交流电源生成含闪变分量的供电电压并施加于电机。供电电压闪变的参数设置为：Am≈ 0.014 A1≈4.16 V、fm≈2s f1=2.76 Hz。注意：设定fm与2s f1近似相等，这是供电电压闪变影响转子故障检测的最不利情况。设定负载转矩为9.9 N·m(近似满载)。
图 11(a)、(b)分别表示us(t)的瞬变波形、细化FFT频谱。转子健康情况下的实验结果示于图 12。其中，图 12(a)、(b)、(c)分别表示is(t)在0~500 Hz、40~60 Hz、335~345 Hz内的细化FFT频谱。
![]()
图 11 供电电压闪变时A相电压的瞬变波形和细化频谱Figure 11. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is flickering![]()
图 12 供电电压闪变且转子健康时的实验结果Figure 12. Experimental results while supply voltage is flickering and rotor is healthy对比图 11与图 8可知，供电电压闪变使us(t)的包络出现脉动，并使其细化频谱在(f1−fm)=47.31 Hz和(f1+fm)=52.80 Hz附近出现谱峰。
根据图 12(a)、(b)和表 2可知，在转子故障主特征频率附近出现明显的谱峰，因此现有的MCSA方法将判断：转子故障。但实际情况是转子健康，仅供电电压闪变而已。这就意味着——现有的MCSA方法是受供电电压闪变影响的，因而将供电电压闪变“误判”为转子故障。
根据图 11(b)可以判定供电电压闪变存在并将影响转子故障检测。因此，需采取进一步措施予以避免。
此时，f1=50.04 Hz、fm=2.76 Hz。以表 2为参考，根据式(11)、(12)、(14)计算出与转子故障特征频率接近的供电电压闪变特征频率：47.28、52.80、144.60、150.12、241.92、247.44、339.23、344.75、436.55、442.07 Hz。上述频率可能混淆转子故障特征频率。对照表 2，可以确定当前转子故障独有的、区别于供电电压闪变的特征频率fRF为44.52、55.56、341.99 Hz。
根据图 12(b)、(c)可知，is(t)的细化频谱在fRF附近并无谱峰。因此，根据本文所提方法可以确认：转子健康，但供电电压闪变。自然，该判断是正确的。
以故障转子替换正常转子，实验结果示于 图 13。其中，图 13(a)—(c)分别表示is(t)在0~ 500 Hz、40~60 Hz、335~345 Hz内的细化FFT频谱。
![]()
图 13 供电电压闪变且转子故障时的实验结果Figure 13. Experimental results while supply voltage is flickering and rotor is faulty根据图 13(a)、(b)和表 2可知，在转子故障主特征频率附近出现明显的谱峰，因此预判：转子故障。根据图 11(b)可以判定供电电压闪变存在并将影响转子故障检测，因此需采取进一步措施。
如前所述，可以确定当前转子故障独有的、区别于供电电压闪变的特征频率fRF为44.52、55.56、341.99 Hz。
根据图 13(b)、(c)可知，is(t)的细化频谱在fRF附近出现谱峰。因此，根据本文所提方法可以确认：转子故障，且供电电压闪变。自然，该判断是正确的。
上述仿真与实验结果表明，供电电压闪变确实可能对转子故障在线检测造成不利影响，而本文所提出的应对方案可予回避。
需要指出，本文所针对的供电电压闪变是由单一频率的正弦调幅波调制而成的，参见式(4)。近年来，风电、光伏等随机、波动性能源的大规模接入电网，使电压闪变的成因趋于复杂，如双频率正弦调幅波调制、单一频率矩形调幅波调制等。这些不同成因、形式的电压闪变同样可能对转子故障在线检测造成不利影响，本文所提出的应对方案仍具参考意义。
5. 结论
1）当供电电压闪变的调幅波频率近似等于两倍转差频率时，异步电动机定子电流信号中将出现闪变特征频率分量，并混淆转子故障特征频率分量，从而对转子故障在线检测产生不利影响，导致基于定子电流信号分析的转子故障在线检测方法失效。
2）揭示了供电电压闪变影响异步电动机转子故障在线检测的机制，推导出了闪变特征频率的解析表达式。
3）以现有的基于定子电流信号分析的转子故障在线检测方法为基础，提出了免于供电电压闪变影响的异步电动机转子故障在线检测方法。相对于现有方法，本文所提出的方法可以免于供电电压闪变的影响，这是其显著优点。
4）异步电动机是在供电电压的激励下运行的，而供电电压是可能闪变并影响转子故障在线检测的。因此，在转子故障在线检测实践中必须考虑“供电电压闪变”这一因素而增加“应对”环节，这是值得广泛关注的。
-
![]()
图 1 供电电压正常时A相电压的瞬变波形和细化频谱
Figure 1. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is normal
![]()
图 2 供电电压正常且转子健康时的仿真结果
Figure 2. Simulation results while supply voltage is normal and rotor is healthy
![]()
图 3 供电电压正常且转子故障时的仿真结果
Figure 3. Simulation results while supply voltage is normal and rotor is faulty
![]()
图 4 供电电压闪变时A相电压的瞬变波形和细化频谱
Figure 4. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is flickering
![]()
图 5 供电电压闪变且转子健康时的仿真结果
Figure 5. Simulation results while supply voltage is flickering and rotor is healthy
![]()
图 6 供电电压闪变且转子故障时的仿真结果
Figure 6. Simulation results while supply voltage is flickering and rotor is faulty
![]()
图 8 供电电压正常时A相电压的瞬变波形和细化频谱
Figure 8. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is normal
![]()
图 9 供电电压正常且转子健康时的实验结果
Figure 9. Experimental results while supply voltage is normal and rotor is healthy
![]()
图 10 供电电压正常且转子故障时的实验结果
Figure 10. Experimental results while supply voltage is normal and rotor is faulty
![]()
图 11 供电电压闪变时A相电压的瞬变波形和细化频谱
Figure 11. Instantaneous waveform and subdivision spectrum of A-phase voltage while supply voltage is flickering
![]()
图 12 供电电压闪变且转子健康时的实验结果
Figure 12. Experimental results while supply voltage is flickering and rotor is healthy
![]()
图 13 供电电压闪变且转子故障时的实验结果
Figure 13. Experimental results while supply voltage is flickering and rotor is faulty
表 1 转子故障特征频率
Table 1 Feature frequencies of rotor fault
Hz (1-2s)f1 (1+2s)f1 (1-4s)f1 (1+4s)f1 [k(1-s) ±s]f1(k=7) (7-8s)f1 (7-6s)f1 48.17 51.83 46.34 53.66 342.68 344.51 
下载: 导出CSV
表 2 转子故障特征频率
Table 2 Feature frequencies of rotor fault
Hz (1−2s)f1 (1+2s)f1 (1−4s)f1 (1+4s)f1 [k(1−s)±s]f1 (k=7) (7−8s)f1 (7−6s)f1 47.28 52.80 44.52 55.56 339.23 341.99
下载: 导出CSV
-
[1] 许伯强, 孙丽玲. 异步电动机故障在线监测与诊断[M]. 北京: 中国电力出版社, 2018. XU Boqiang, SUN Liling. Online monitoring and diagnosis of induction motor faults[M]. Beijing: China Electric Power Press, 2018(in Chinese).
[2] EL-DINE ATTA M E, IBRAHIM D K, GILANY M I. Broken bar fault detection and diagnosis techniques for induction motors and drives: state of the art[J]. IEEE Access, 2022, 10: 88504-88526. DOI: 10.1109/ACCESS.2022.3200058
[3] 李睿彧, 刘飞, 梁霖, 等. 基于参数优化变分模态分解的交流变频电机转子断条故障识别方法[J]. 电工技术学报, 2021, 36(18): 3922-3933. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202118018.htm LI Ruiyu, LIU Fei, LIANG Lin, et al. Fault identification of broken rotor bars for the variable frequency AC motor based on parameter optimized variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3922-3933(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202118018.htm
[4] LI Haiyang, FENG Guojin, ZHEN Dong, et al. A normalized frequency-domain energy operator for broken rotor bar fault diagnosis[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3500110.
[5] WANG Wanding, SONG Xiangjin, LIU Guohai, et al. Induction motor broken rotor bar fault diagnosis based on third-order energy operator demodulated current signal[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 1052-1059. DOI: 10.1109/TEC.2021.3121788
[6] AGAH G R, RAHIDEH A, KHODADADZADEH H, et al. Broken rotor bar and rotor eccentricity fault detection in induction motors using a combination of discrete wavelet transform and Teager-Kaiser energy operator[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2199-2206.
[7] YANG C, KANG T J, HYUN D, et al. Reliable detection of induction motor rotor faults under the rotor axial air duct influence[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2493-2502. DOI: 10.1109/TIA.2013.2297448
[8] ANTONINO-DAVIU J A, QUIJANO-LÓPEZ A, RUBBIOLO M, et al. Advanced analysis of motor currents for the diagnosis of the rotor condition in electric motors operating in mining facilities[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3934-3942. DOI: 10.1109/TIA.2018.2818671
[9] GARCIA-CALVA T A, MORINIGO-SOTELO D, DE JESUS ROMERO TRONCOSO R, et al. Fundamental frequency normalization for reliable detection of rotor and load defects in VSD-fed induction motors[J]. IEEE Transactions on Energy Conversion, 2022, 37(2): 1467-1474. DOI: 10.1109/TEC.2021.3124803
[10] 谢颖, 单雪婷, 郭金鹏, 等. 笼型转子导条断裂引发电机各场量变化与故障程度关联性研究[J]. 中国电机工程学报, 2017, 37(14): 4222-4231. DOI: 10.13334/j.0258-8013.pcsee.162507 XIE Ying, SHAN Xueting, GUO Jinpeng, et al. The relationship study between field changes and faulty condition in squirrel-cage induction motor with broken bars fault[J]. Proceedings of the CSEE, 2017, 37(14): 4222-4231(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.162507
[11] 许伯强, 孙丽玲. 异步电动机转子故障与负荷波动的协同识别方法[J]. 中国电机工程学报, 2016, 36(23): 6518-6527. DOI: 10.13334/j.0258-8013.pcsee.160019 XU Boqiang, SUN Liling. Concurrent discrimination of rotor fault and load oscillation in induction motors[J]. Proceedings of the CSEE, 2016, 36(23): 6518-6527(in Chinese). DOI: 10.13334/j.0258-8013.pcsee.160019
[12] PARK Y, JEONG M, LEE S B, et al. Influence of blade pass frequency vibrations on MCSA-based rotor fault detection of induction motors[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2049-2058.
[13] SPYROPOULOS D V, PANAGIOTOU P A, ARVANITAKIS I, et al. Extraction of frequency information for the reliable screening of rotor electrical faults via torque monitoring in induction motors[J]. IEEE Transactions on Industry Applications, 2021, 57(6): 5949-5958.
[14] PARK Y, YANG C, KIM J, et al. Stray flux monitoring for reliable detection of rotor faults under the influence of rotor axial air ducts[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7561-7570.
[15] LEE S B, SHIN J, PARK Y, et al. Reliable flux-based detection of induction motor rotor faults from the fifth rotor rotational frequency sideband[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 7874-7883.
[16] RAFAQ M S, SHAIKH M F, PARK Y, et al. Reliable airgap search coil based detection of induction motor rotor faults under false negative motor current signature analysis indications[J]. IEEE Transactions on Industrial Informatics, 2022, 18(5): 3276-3285.
[17] 唐求, 滕召胜, 高云鹏, 等. 基于S变换的平方检测法测量电压闪变[J]. 中国电机工程学报, 2012, 32(7): 60-67. http://ntps.epri.sgcc.com.cn/djgcxb/CN/Y2012/V32/I7/60 TANG Qiu, TENG Zhaosheng, GAO Yunpeng, et al. Voltage flicker measurement using square demodulation method based on S-transform [J]. Proceedings of the CSEE, 2012, 32(7): 60-67(in Chinese). http://ntps.epri.sgcc.com.cn/djgcxb/CN/Y2012/V32/I7/60
[18] 张民谣, 高云鹏, 吴聪, 等. 基于自适应变分模式分解的非稳态电压闪变包络参数检测[J]. 电工技术学报, 2021, 36(3): 599-622. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202103016.htm ZHANG Minyao, GAO Yunpeng, WU Cong, et al. Non-stationary voltage flicker envelope parameters detection based on adaptive variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 599-622(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202103016.htm
[19] 邱衍江, 张超, 张新燕, 等. 基于能量算子和最大旁瓣衰减自卷积窗函数频谱校正的电压闪变参数识别技术及其在风电场的应用研究[J]. 电子与信息学报, 2021, 43(8): 2214-2223. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX202108012.htm QIU Yanjiang, ZHANG Chao, ZHANG Xinyan, et al. Flicker parameters detection technology based on improved energy operator of optimized sampling interval and MSLD-SCW function spectrum correction in and its application in wind farms[J]. Journal of Electronics & Information Technology, 2021, 43(8): 2214-2223(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX202108012.htm
[20] CHEN Peng, XIE Ying. Harmonics analysis of air-gap magnetic field of induction motors with stator inter-turn fault[J]. IEEE Transactions on Magnetics, 2022, 58(7): 8202409.
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
下载:
