Single-phase Single-stage Coupled Inductor Split-source Boost Inverter
-
摘要: 面对全球资源日渐紧缺、环境问题日益严重、传统化石能源开发利用越发困难等新挑战,世界各国都在大力探索、发展新能源发电技术,以新能源为主体的新型电力系统是未来电力系统的发展方向。该文提出一种单相单级式耦合电感型分裂源升压逆变器及其调制策略,所提出的变换器具有如下特点:1)采用Δ型耦合电感,极大地提升变换器的输出电压增益,并具有高输出电压增益调节自由度。2)采用双Buck结构,有效抑制逆变桥臂直通电流,降低死区时间配置要求,提高变换器可靠性。3)高输出电压增益条件下具有高调制系数,从而有效提升输出电压波形质量。该文对该变换器的拓扑结构、工作原理、调制策略和输出特性等进行详细分析,通过仿真与实验验证变换器的可行性与有效性。Abstract: This paper proposes a single-phase single-stage couple inductor split-source Boost inverter suitable for new energy power generation. The proposed converter has the following characteristics: 1) High output voltage Boost factor by adopting the Δ-source coupled inductor structure, as well as a more free degree of freedom in adjusting the output voltage gain; 2) improved reliability of the inverter by implementing the dual-Buck structure to suppress the shoot-through current; 3) a high modulation factor under the condition of high output voltage gain, thereby improving the quality of the output voltage waveform. Comprehensive working principles, modulation strategy, steady-state analysis and parameter design guideline are introduced; both simulation and experimental results are presented to confirm the characteristics of the proposed topology.
-
Keywords:
- split-source inverter (SSI) /
- dual-Buck inverter /
- high Boost factor /
- Boost inverter
-
0. 引言
面对全球资源日渐紧缺、环境问题日益严重、传统化石能源开发利用越发困难等新挑战,世界各国都在大力探索、发展新能源发电技术,以新能源为主体的新型电力系统是未来电力系统的发展方向[1-3]。通常情况下,典型新能源(如太阳能、风能、化学能等)设备的输出直流电压等级较低,而传统电压型逆变器为降压型逆变器,为使新能源发电设备输出的直流电逆变后输出得到适用于民用电(110或220 V)的并网电压,需要在新能源发电设备后级联DC-DC升压变换器,再经逆变器产生适用于并网的电压等级,称为两级式升压逆变器[4-6]。然而,在这类两级式升压逆变器系统中,前级DC-DC升压变换器使用的高频开关及其伴随的驱动电路增加系统成本,额外使用的电容、电感不可避免地增加系统体积重量。为解决这些问题,通过合适的拓扑改造及调制设计,将前级DC-DC升压的功能集成到后级逆变器,可以获得同时具备升压和逆变功能的单级式升压逆变器。一种典型的单级升压逆变器为Z源逆变器[7](Z-source inverter,ZSI),ZSI具有单级升压逆变的功能,其逆变桥同一桥臂的开关管允许直通,避免设置死区时间,这些优点使ZSI得到广泛应用[8-11]。然而,ZSI高电压增益条件下需要较大的直通占空比,这将降低ZSI的调制系数,导致母线电压利用率降低,并使得输出电压波形质量变差,且ZSI的非连续输入电流会引起较大的输入冲击电流[12]。面对这些问题,一种解决思路是调整电路拓扑结构,使变换器能够在低直通占空比的条件下实现高增益,如添加开关电感/电容结构[13-14],二极管/电容辅助结构[15]等。但过多的器件数量将导致变换器体积重量的进一步增加。
文献[16]提出另一种典型的单级式升压逆变器,称为分裂源逆变器(split-source inverter,SSI)。SSI由1个电感、1个电容、2个二极管以及1个全桥逆变桥臂构成。SSI具有单级升压逆变、输入电流连续、输入电压源与逆变桥共地等优点。相比于传统阻抗源逆变器,如(准)Z源逆变器,(准)开关升压逆变器,SSI仅使用2个无源器件,升压侧仅使用2个二极管,使得SSI具有更紧凑的结构及更低的器件使用成本;此外,SSI可以在获得高输出电压增益的同时保持较高的调制系数,在保证高电压波形质量的同时实现较高的输出电压增益。
基于这些优点,SSI得到广泛的研究与应用,文献[17]提出SSI的三相型式,并提出相应调制策略消除输入电流低频纹波。文献[18]通过使用2个开关管代替SSI输入侧的2个二极管,有效抑制SSI输入侧二极管电流高频换向的问题,提升变换器效率,但引入的开关管及伴随的驱动电路增加了变换器成本。文献[19]通过调整SSI输入侧二极管及逆变桥开关管位置,构造一种简化型SSI(simplified split-source inverter,S3I),该S3I的输出电压增益为SSI的2倍。文献[20]提出一种分裂Y源逆变器,显著提高变换器的输出电压增益。文献[21]针对SSI直流母线电压利用率低的问题,提出一种增强型SSI(active split-source inverter,ASSI),但该ASSI的缺点在于额外使用2个MOS管,使得变换器成本进一步增加。文献[22]将九开关结构同SSI结合起来,构造一种新型单输入双输出升压逆变器。然而,目前各类改进型SSI仍然受制于相对较低的升压能力,并且需要设置死区时间以避免逆变桥臂开关管直通,然而死区时间的引入会不可避免地导致输出电压波形质量变差。针对这些问题,本文提出一种单相单级式耦合电感型分裂源升压逆变器拓扑,该拓扑具有以下特点:
1)采用Δ型耦合电感代替SSI的电感,极大提升变换器的输出电压增益,既可以通过调整占空比改变输出电压增益,也可以通过调节耦合电感匝数来改变输出电压增益,输出电压增益调节自由度高。
2)采用双降压逆变结构(dual-Buck inverter,DBI),可以有效抑制逆变桥臂直通电流,降低死区时间配置要求,提高变换器可靠性。
3)高输出电压增益条件下具有高调制系数,从而提升输出电压波形质量。
本文详细阐述该逆变器的工作原理,并通过仿真与实验验证理论分析的正确性。
1. 拓扑结构与工作原理
1.1 电路拓扑
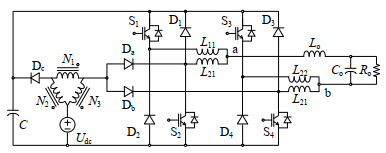
本文提出的单相单级式耦合电感型分裂源升压逆变器(delta-source split-source inverter,DSSI)如图 1所示,直流侧由电压源Udc、3个二极管(Da、Db、Dc)、Δ型耦合电感以及电容C构成;逆变侧由4个开关管S1-S4、4个二极管D1-D4和4个限流电感L11、L21、L12、L22构成的双降压结构逆变桥,LC滤波器Lo,Co以及负载电阻Ro构成。升压侧采用的Δ型耦合电感将Udc升压后作为DBI的输入,逆变生成交流电经LC滤波输出至负载。DBI能有效抑制桥臂直通时产生的直通电流,提高电路可靠性。
1.2 工作原理
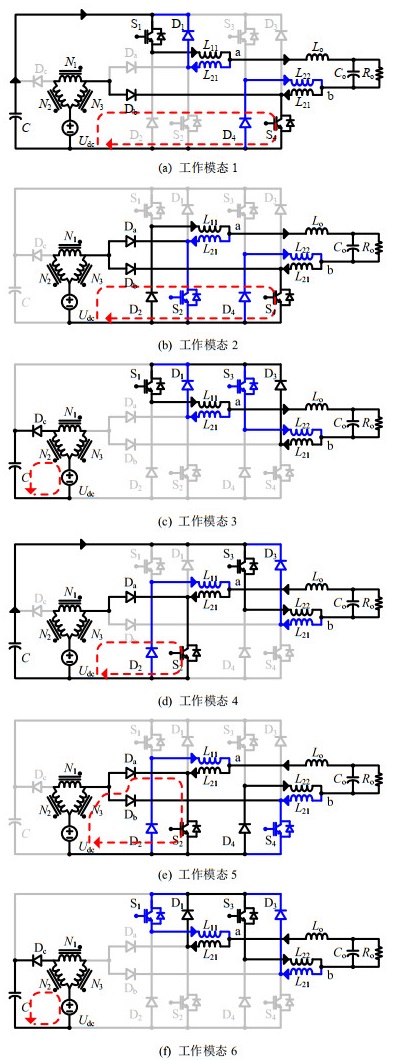
电路各工作模态等效电路如图 2所示,图中红线为耦合电感充/放电回路,灰线表示无电流流通,蓝线为逆变过程中产生的电流通路。模态1至模态3输出电压为正(规定电流方向往右为正),此时L11、L12、Lo为滤波电感;模态4至模态5输出电压为负,此时L21、L22、Lo为滤波电感。假设L11 = L12 = L21 = L22 = L,则等效滤波电感Leq = 2L + Lo。
1)工作模态1:如图 2(a)所示。在该模态中,开关管S1、S4开通,S2、S3关断;二极管Db、D1、D4开通,Da、Dc、D2、D3关断。输入电压源经Db、S4对耦合电感充电,电容C经S1、L11,L12、S4对负载放电,输出电压为正。
2)工作模态2:如图 2(b)所示。在该模态中,开关管S2、S4开通,S1、S3关断;二极管Da、Db、D2、D4开通,Dc、D1、D3关断。输入电压源经Db、S4对耦合电感充电,电感L11、L12及Lo对负载放电,输出电压为正。
3)工作模态3:如图 2(c)所示。在该模态中,开关管S1、S3开通,S2、S4关断;二极管D1、D3开通,Da、Db、D2、D4关断。输入电压源与耦合电感N2绕组经Dc同时对电容C充电。电感L11、L12及Lo对负载放电,输出电压为正。
4)工作模态4:如图 2(d)所示。在该模态中、开关管S2、S3开通,S1、S4关断;二极管Da、D2、D3开通,Db、Dc、D1、D4关断。输入电压源经Da、S2对耦合电感充电,电容C经S3、L22、L21、S2对负载放电,输出电压为负。
5)工作模态5:如图 2(e)所示。在该模态中、开关管S2、S4开通,S1、S3关断;二极管Da、Db、D2、D4开通,Dc、D1、D3关断。输入电压源经Da、S2对耦合电感充电,电感L21、L22及Lo对负载放电,输出电压为负。
6)工作模态6:如图 2(f)所示。在该模态中、开关管S1、S3开通,S2、S4关断;二极管D1、D3开通,Da、Db、D2、D4关断。输入电压源与耦合电感N2绕组经Dc同时对电容C充电。电感L21、L22及Lo对负载放电,输出电压为负。
1.3 控制策略
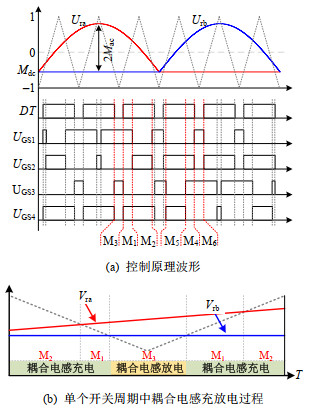
图 3为本文所提逆变器所采用的控制策略及其关键波形图。
图 3(a)中,调制波Ura、Urb的幅值为2Mac,偏移量为Mdc(−1 < Mdc < 1),用以控制直流侧母线电容的充电时间恒定。Mac与Mdc的关系为
$$ 0 \lt 2{M_{{\text{ac}}}} \leqslant 1 - {M_{{\text{dc}}}} \lt 2 $$ (1) 调制波Ura大于三角载波时,驱动S1导通,S2与S1互补导通;调制波Urb大于三角载波时,驱动S3导通,S4与S3互补导通。在一个开关周期内,当载波同时小于调制波时,S1、S3同时导通,此时输入电压源与耦合电感N2绕组经Dc同时对电容C充电,对应模态3与模态6,其余时间耦合电感皆处于充电状态,如图 3(b)所示。定义耦合电感充电占空比为D,其表达式如式(2)所示:
$$ D = \frac{{1 - {M_{{\text{dc}}}}}}{2} $$ (2) 由式(2)可知,当选定调制波偏移量Mdc,耦合电感的充电占空比即为定值,即一个开关周期中,耦合电感充放电的时间固定,与传统的正弦充电占空比相比[22],固定充电占空比可以简化电路分析,同时降低输出电压纹波以及器件电压应力。
1.4 双降压结构
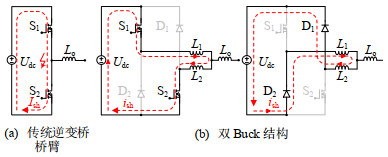
传统的逆变桥桥臂结构如图 4(a)所示,设开关管S1与S2的导通电阻为rDS,当桥臂上下两管同时导通时,流过开关管的电流迅速增大,将击穿开关管,导致变换器故障。此时直通电流大小为
$$ {I_{{\text{sh}}}} = \frac{{{U_{{\text{dc}}}}}}{{2{r_{{\text{DS}}}}}} $$ (3) 采用双Buck降压结构时,当桥臂上下两管同时导通时,由于限流电感L1与L2的存在,流过开关管的电流不能瞬时增大,此时直通电流增长率为
$$ \frac{{\Delta {i_{{\text{sh}} + }}}}{{\Delta {t_{{\text{sh}}}}}} = \frac{{{U_{{\text{dc}}}} - 2{i_{{\text{sh}}}}{r_{{\text{DS}}}}}}{{{L_1} + {L_2}}} $$ (4) 由式(4)可知,采用双降压结构,可以使得逆变桥臂的开关管能够承受一定的桥臂直通时间而不被击穿,从而提升电路的可靠性。该承受时间与所采用开关管的耐流值、开关管导通电阻值、逆变桥输入电压值及限流电感的感值大小有关。
桥臂开关管均关断时,限流电感将其在直通时储存的能量,通过二极管D1与D2反馈回输入侧,此时,流过限流电感的电流降低率为
$$ \frac{{\Delta {i_{{\text{sh}} - }}}}{{\Delta {t_{{\text{dt}}}}}} = \frac{{{U_{{\text{dc}}}} - 2{U_{\text{F}}}}}{{{L_1} + {L_2}}} $$ (5) 式中UF为二极管的导通压降。
逆变桥臂直通时,直流母线电压释放的能量储存在限流电感中,这会产生电路逆变侧的电流环流,该环流的大小随直通次数的增大而累计增大,因此,为保证电路可靠性,在每个开关周期中,应设置一定的死区时间,释放限流电感的能量。流过限流电感的电流大小可定义为
$$ {i_{{\text{sh}}}} = \frac{{{U_{{\text{dc}}}}}}{{{L_1} + {L_2}}}(\sum {{t_{{\text{sh}}}}} - \sum {{t_{{\text{dt}}}}} ) $$ (6) 式(6)中忽略二极管的导通压降及开关管寄生
电阻的压降,$ \sum {{t_{{\text{sh}}}}} $和$ \sum {{t_{{\text{dt}}}}} $分别为直通状态及死区状态的累计时间,当$ \sum {{t_{{\text{sh}}}}} \leqslant \sum {{t_{{\text{dt}}}}} $时,则ish能维持为0,需要注意的是,每个开关周期中不一定会发生直通状态,但在每个开关周期中设置一个较小的死区时间,即可满足限流电感能量释放要求,因此,该变换器设定300 ns的死区时间。
1.5 输出特性
由1.2节模态分析可知,在耦合电感充电期间有:
$$ {U_{{\text{dc}}}} = {U_{{\text{N3}}}} $$ (7) 耦合电感放电时,由基尔霍夫电压定律(Kirchhoff voltage law,KVL)可得:
$$ {U_{{\text{dc}}}} = {U_{\text{C}}} + \frac{{{N_2}}}{{{N_3}}}{U_{{\text{N3}}}} $$ (8) 结合式(7)、(8),由电感电压伏秒平衡原理可得:
$$ {U_{{\text{dc}}}}DT + \frac{{{N_3}({U_{{\text{dc}}}} - {U_C})}}{{{N_2}}}(1 - D)T = 0 $$ (9) 由式(9)可求出直流母线电容电压UC为
$$ {U_{\text{C}}} = \frac{{{N_3} + ({N_2} - {N_3})D}}{{{N_3}(1 - D)}}{U_{{\text{dc}}}} $$ (10) 则对应的直流电压增益Gdc为
$$ {G_{{\text{dc}}}} = \frac{{{U_C}}}{{{U_{{\text{dc}}}}}} = \frac{{1 + \lambda D}}{{1 - D}},\quad \lambda = \frac{{{N_2} - {N_3}}}{{{N_3}}} $$ (11) 交流侧输出电压幅值为
$$ {U_{\text{o}}} = {M_{{\text{ac}}}}\frac{{1 + \lambda D}}{{1 - D}}{U_{{\text{dc}}}} $$ (12) 对应的交流输出电压增益为
$$ {G_{{\text{ac}}}} = {G_{{\text{dc}}}}{M_{{\text{ac}}}} = {M_{{\text{ac}}}}\frac{{1 + \lambda D}}{{1 - D}} $$ (13) 所提变换器输入电流为
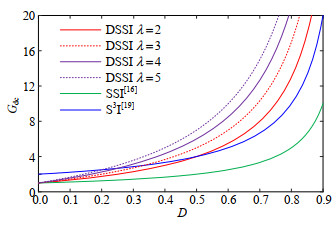
$$ {I_{{\text{in}}}} = \frac{{M_{{\text{ac}}}^2{{(1 + \lambda D)}^2}{U_{{\text{dc}}}}}}{{2{{(1 - D)}^2}R}} $$ (14) 图 5绘制所提逆变器在不同匝比下的直流增益曲线,横坐标为占空比D,纵坐标为直流电压增益Gdc。由图 5可知,所提逆变器的直流增益均高于传统SSI,设置匝比为2,D大于0.5时,所提逆变器的直流增益要高于S3I[19],设置匝比大于2,D大于0.3时,所提逆变器的直流增益均高于S3I。
与传统的阻抗源升压逆变器如准Z源逆变器(quasi-Z source inverter,qZSI)和准开关升压逆变器(quasi-switch Boost inverter,qSBI)相比,本文所提逆变器的交流电压增益不仅可以通过控制占空比来调节,还可以通过设置合适的绕组比来调节输出电压增益,输出电压增益调节自由度高。图 6为qZSI、qSBI与所提逆变器电压增益G与调制系数Mac的关系曲线。由于qZSI和qSBI的调制系数Mac随着其充电占空比D的增大而减小(Mac = 1 − D),使得qZSI和qSBI的电压增益随着调制系数的增大而减小,而过低的调制系数会使交流输出波形畸变,输出波形质量降低。在所提逆变器中,电压增益可随着调制系数的增大而增大,使电路在高电压增益的前提下保证输出波形质量。
此外,考虑电路器件中寄生参数的影响,非理想状态下的直流电压增益系数为
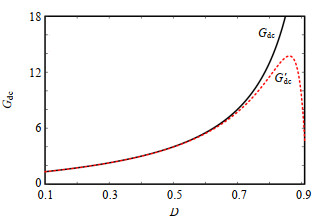
$$ \left\{ \begin{array}{l} {{G}_{{\text{dc}}}^{'}} = {G_{{\text{dc}}}} - \frac{{{U_{\text{F}}}{G_{{\text{dc}}}}}}{{{U_{{\text{dc}}}}}} + \frac{{({A_1}{r_{\text{L}}} + {A_2}{r_{{\text{DS}}}} - {r_{\text{C}}}){D^2}G_{{\text{dc}}}^2}}{{2R}} \hfill \\ {A_1} = \frac{{({N_3} - {N_2})D - N_3^2}}{{N_3^2(1 - D)}} \hfill \\ {A_2} = \frac{{{N_2}D}}{{{N_3}(D - 1)}} \hfill \\ \end{array} \right. $$ (15) 式中:rL为电感寄生电阻;rC为电容等效串联电阻;rDS为开关管导通电阻;UF为二极管导通压降。结合式(11)、(15),图 7为考虑器件寄生参数情况下的直流电压增益曲线。比较所提逆变器的理想直流电压增益与非理想直流电压增益,由于寄生参数的影响,当占空比高于0.85时,所提逆变器的实际电压增益将呈现下降趋势。
2. 参数设计
2.1 电容设计
根据1.2节中电路构造模态的分析,模态3与模态6中,输入电压源与耦合电感同时对直流母线电容充电,此时其电压应力最大,如式(16)所示:
$$ {U_{\text{C}}} = \frac{{1 + \lambda D}}{{1 - D}}{U_{{\text{dc}}}} $$ (16) 由式(16)可得,直流母线电容容值应设计[23]为
$$ C \geqslant \frac{P}{{2{{\rm{ \mathsf{ π} }} }{f_{\text{o}}}{U_{\text{C}}}\Delta {U_{\text{C}}}}} $$ (17) 式中:UC为电压应力;ΔUC为电压纹波;fo为输出电压频率;P为输出功率。
2.2 耦合电感设计
耦合电感中的励磁电感通过在模态1、模态2、模态4与模态5中储存能量,在模态3与模态6释放能量至直流母线电容以实现直流侧电压升压效果。励磁电感充电时,励磁电流峰值为
$$ {I_{{\text{Lm_pk}}}} = \frac{{{U_{{\text{Lm}}}}}}{{{L_{\text{m}}}}}DT = \frac{{{U_{{\text{N1}}}}}}{{{L_{\text{m}}}}}DT = \frac{{{N_1}DT{U_{{\text{dc}}}}}}{{{N_3}{L_{\text{m}}}}} $$ (18) 由式(18)可得励磁电流纹波为
$$ \Delta {i_{{\text{Lm}}}} = \frac{1}{2}{I_{{\text{Lm_pk}}}} = \frac{{{N_1}DT{U_{{\text{dc}}}}}}{{2{N_3}{L_{\text{m}}}}} \leqslant x\% {I_{{\text{Lm}}}} $$ (19) 由式(19)可知,励磁电感感值的设计表达式为
$$ {L_{\text{m}}} \geqslant \frac{{{N_1}DT{U_{{\text{dc}}}}}}{{2{N_3}x\% {I_{{\text{Lm}}}}}} $$ (20) 2.3 滤波电感设计
所提逆变器在每半个调制波周期中各有2个限流电感起滤波作用,则等效滤波电感如式(21)所示:
$$ {L_{{\text{eq}}}} = {L_{11}} + {L_{12}} + {L_{\text{o}}} = {L_{21}} + {L_{22}} + {L_{\text{o}}} $$ (21) 该等效滤波电感值由输出电压,输出电流及输出电流纹波决定,则其感值应满足以下条件:
$$ {L_{{\text{eq}}}} \geqslant \frac{{{U_{\text{o}}}(1 - D)T}}{{\Delta {i_{\text{L}}}}} = \frac{{{U_{\text{o}}}(1 - D)T}}{{x\% {I_{\text{o}}}}} $$ (22) 2.4 功率开关管及二极管设计
功率开关管及二极管的电压应力及电流应力表达式如表 1所示。
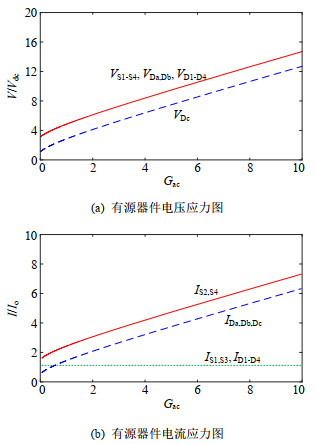
表 1 功率开关管及二极管电压电流应力Table 1. Voltage/Current Stresses on Switch and Diode应力种类 功率开关管 二极管 电压应力 $ {U_{{\text{S1 - 4}}}} = \frac{{1 + \lambda D}}{{1 - D}}{U_{{\text{dc}}}} $ $ \left\{ \begin{array}{l} {U_{{\text{Da}}}} = {U_{{\text{Db}}}} = \frac{{1 + \lambda D}}{{1 - D}}{U_{{\text{dc}}}} \hfill \\ {U_{{\text{Dc}}}} = {U_{\text{C}}} - {U_{{\text{dc}}}} + {U_{{\text{N2}}}} \hfill \\ {U_{{\text{D1}}}} = {U_{{\text{D2}}}} = {U_{{\text{D3}}}} = {U_{{\text{D4}}}} = {U_{\text{C}}} \hfill \\ \end{array} \right. $ 电流应力 $ \left\{ \begin{array}{l} {I_{{\text{S1}}}} = {I_{{\text{S3}}}} = {I_{\text{o}}} \hfill \\ {I_{{\text{S2}}}} = {I_{{\text{S4}}}} = {I_{\text{o}}} + {I_{{\text{in}}}} \hfill \\ \end{array} \right. $ $ \left\{ \begin{array}{l} {I_{{\text{Da}}}} = {I_{{\text{Db}}}} = {I_{{\text{Dc}}}} = {I_{{\text{in}}}} \hfill \\ {I_{{\text{D1}}}} = {I_{{\text{D2}}}} = {I_{{\text{D3}}}} = {I_{{\text{D4}}}} = {I_{\text{o}}} \hfill \\ \end{array} \right. $ 根据表 1,功率开关管及二极管的电压应力与输入电压的比值、电流应力与输出电流的比值与交流电压增益Gac关系绘制于图 8。由图 8可以看出,有源器件的电压和电流应力随着交流输出电压增益的增大而增加。
3. 损耗分析
本节对本文提出的逆变器进行损耗分析,所提逆变器的整体损耗可分为开关管损耗、二极管损耗、电感损耗和电容损耗。其中,开关器件损耗可分为开关管开通与关断过程中产生的开关损耗,以及导通时产生的导通损耗,根据逆变器工作模态分析,电路中开关器件的电压应力和电流应力分别为
$$ \left\{ \begin{array}{l} {U_{{\text{S1 - 4}}}} = \frac{{1 + \lambda D}}{{1 - D}}{U_{{\text{dc}}}} \hfill \\ {I_{{\text{S}}1}} = {I_{{\text{S3}}}} = {I_{\text{o}}} = \frac{{(1 + \lambda D)D{U_{{\text{dc}}}}}}{{(1 - D)R}} \hfill \\ {I_{{\text{S2}}}} = {I_{{\text{S}}4}} = {I_{\text{o}}} + {I_{{\text{in}}}} = \frac{{[2 + ( - 1 + 2\lambda )D + {\lambda ^2}{D^3}]D{U_{{\text{dc}}}}}}{{2{{(1 - D)}^2}R}} \hfill \\ \end{array} \right. $$ (23) 开关管导通时流过的电流有效值为
$$ {I_{{\text{S(RMS)}}}} = \sqrt {\frac{1}{T}(\int_0^{{T_1}} {i_{\text{L}}^2(t){\text{d}}t} + \int_0^{{T_2}} {i_{\text{o}}^2(t){\text{d}}t} )} $$ (24) 式中:T1为开关管在耦合电感充电时的导通时间;T2为开关管在耦合电感放电时的开通时间。
开关管的开关损耗表达式为
$$ {P_{{\text{switching}}}} = \frac{{{U_{\text{S}}}{I_{\text{S}}}}}{2}({t_{{\text{on}}}} + {t_{{\text{off}}}}){f_{\text{s}}} $$ (25) 式中ton、toff分别为开关管开通和延迟延迟时间。
开关管的导通损耗表达式为
$$ {P_{{\text{conduction}}}} = I_{{\text{S(RMS)}}}^2{r_{{\text{DS}}}} $$ (26) 开关管的整体损耗表达式为
$$ {P_{{\text{S - LOSS}}}} = {P_{{\text{switching}}}} + {P_{{\text{conduction}}}} $$ (27) 二极管导通时流过的电流有效值和平均值为
$$ \left\{ \begin{array}{l} {I_{{\text{D(AVG)}}}} = \frac{1}{T}(\int_0^{{T_3}} {{i_{\text{D}}}(t){\text{d}}t} + \int_0^{{T_4}} {{i_{\text{D}}}(t){\text{d}}t} ) \hfill \\ {I_{{\text{D(RMS)}}}} = \sqrt {\frac{1}{T}(\int_0^{{T_3}} {i_{\text{D}}^2(t){\text{d}}t} + \int_0^{{T_4}} {i_{\text{D}}^2(t){\text{d}}t} )} \hfill \\ \end{array} \right. $$ (28) 式中T3、T4分别为二极管在耦合电感充电和放电时的导通时间。
二极管由于导通电压降UF和寄生电阻rD产生的损耗为
$$ \left\{ \begin{array}{l} {P_{{\text{UF - LOSS}}}} = {I_{{\text{D(AVG)}}}}{U_{\text{F}}} \hfill \\ {P_{{\text{rD - LOSS}}}} = I_{{\text{D(RMS)}}}^2{r_{\text{D}}} \hfill \\ \end{array} \right. $$ (29) 则二极管的整体损耗表达式为
$$ {P_{{\text{D - LOSS}}}} = {P_{{\text{VF - LOSS}}}} + {P_{{\text{rD - LOSS}}}} $$ (30) 所提逆变器的电感损耗可分为铜耗和铁耗,相比于电感铜耗,电感铁耗在总电感损耗中占比很小,因此电感铜耗可认为近似等于总电感损耗。流过DSSI变换器中电感的电流有效值表达式为
$$ \left\{ \begin{array}{l} {I_{{\text{L1(RMS)}}}} = \sqrt {\frac{1}{T}(\int_0^{{T_5}} {i_{{\text{N1}}}^2(t){\text{d}}t} + \int_0^{{T_6}} {i_{{\text{N1}}}^2(t){\text{d}}t} )} \hfill \\ {I_{{\text{L2(RMS}})}} = \sqrt {\frac{1}{T}\int_0^{(1 - D)T} {i_{{\text{in}}}^2(t){\text{d}}t} } \hfill \\ {I_{{\text{L3(RMS}})}} = \sqrt {\frac{1}{T}\int_0^{DT} {i_{{\text{in}}}^2(t){\text{d}}t} } \hfill \\ {I_{{\text{L11 - L22}}({\text{RMS}})}} = \sqrt {\frac{1}{T}\int_0^{{T_7}} {i_{\text{o}}^2(t){\text{d}}t} } \hfill \\ \end{array} \right. $$ (31) 式中:IL1(RMS)—IL3(RMS)为流过耦合电感各绕组的电流有效值;T5为耦合电感绕组N1在耦合电感充电时的导通时间;T6为耦合电感绕组N1在耦合电感放电时的导通时间;T7为限流电感的导通时间。
因此,电感的损耗表达式为
$$ {P_{{\text{L - LOSS}}}} = I_{{\text{L(RMS)}}}^2{r_{\text{L}}} $$ (32) 根据逆变器工作模态分析,流过电容的电流有效值表达式为
$$ {I_{{\text{C(RMS)}}}} = \sqrt {\frac{1}{T}(\int_0^{{T_8}} {i_{\text{C}}^2(t){\text{d}}t} + \int_0^{{T_9}} {i_{\text{C}}^2(t){\text{d}}t} )} $$ (33) 式中:T8为电容充电时间;T9为耦合电感充电过程中电容的充电时间。
因此,电容的损耗表达式为
$$ {P_{{\text{C - LOSS}}}} = I_{{\text{C(RMS)}}}^2{r_{\text{C}}} $$ (34) 基于上述各器件功率损耗分析和公式推导,所提逆变器的整体损耗表达式为
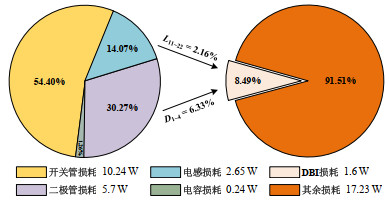
$$ {P_{{\text{total - LOSS}}}} = {P_{{\text{S - LOSS}}}} + {P_{{\text{D - LOSS}}}} + {P_{{\text{L - LOSS}}}} + {P_{{\text{C - LOSS}}}} $$ (35) 根据上述损耗分析计算,在Mac = 0.65,Mdc = −0.4,输出电压有效值Uo(rms) = 110 V,负载电阻R = 50 Ω条件下,所提逆变器的损耗分布如图 9所示。由图 9可知,有源器件的损耗为逆变器整体损耗的主要组成部分,约占84.67%,无源器件损耗占比较小,约为15.33%。其中,双降压结构(dual-Buck inverter,DBI)的损耗包括4个限流电感L11-L22与4个二极管D1-D4的损耗,该部分损耗仅占总损耗的8.49%,在逆变器总损耗中占比较小,但DBI的引入可以提高变换器的可靠性,因此DBI相应产生的损耗在一定程度上是可以接受的。
4. 仿真与实验验证
4.1 仿真验证
为验证前述理论分析中所提逆变器的工作特性,采用PSIM软件对所提逆变器进行仿真验证。表 2给出相应的仿真参数。
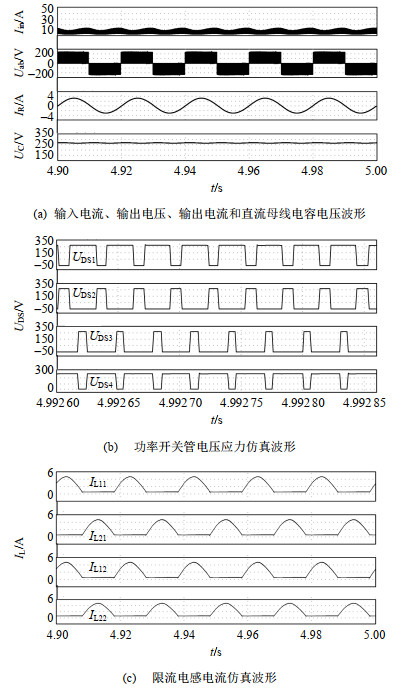
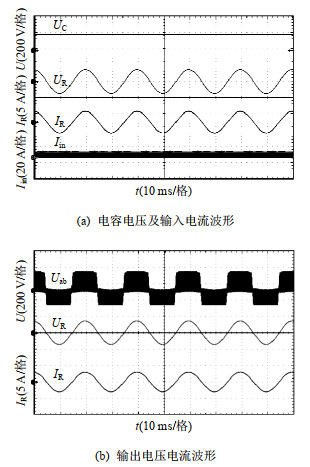
表 2 仿真模型参数Table 2. Parameters of the simulation参数 数值 输入电压Udc/V 36 直流母线电容C/μF 860 限流电感L11—L22/μH 100 滤波电感Lo/mH 10 滤波电容Co/μF 3 负载电阻(水泥电阻)Ro/Ω 50 耦合电感匝比N1 : N2 : N3 40 : 60 : 20 励磁电感Lm/mH 2 开关频率fs/kHz 30 调制比Mac 0.65 偏移量Mdc −0.4 图 10为本文所提逆变器在表 2参数下获得的仿真波形。图 10(a)中,直流升压侧直流母线电容的电压UC升压至280 V,输出电流IR的幅值为3.7 A。相对应的直流电压增益与交流电压增益均与式(11)、(13)吻合。图 10(b)中展示所提逆变器中功率开关管的电压应力仿真波形,这些有源器件的电压应力仿真结果均与表 1中的结果吻合。图 10(c)给出限流电感L11-L22的电流波形图。
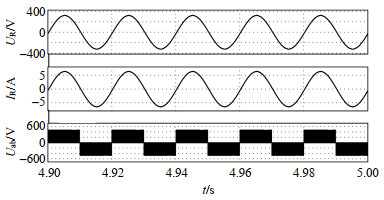
图 11为所提逆变器直流输入30 V,交流输出220 V/50 Hz微型光伏逆变工况下的仿真波形,此时耦合电感匝比设置为N1 : N2 : N3 = 50 : 60 : 10,调制比Mac = 0.695,偏移量Mdc = −0.4。图中交流输出电压UR的有效值为220 V,频率为50 Hz,输出电流IR有效值为4.4 A,桥臂电压Uab幅值为450 V。相对应的直流电压增益和交流电压增益均与理论值相一致。
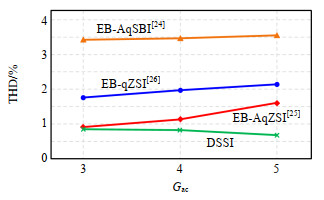
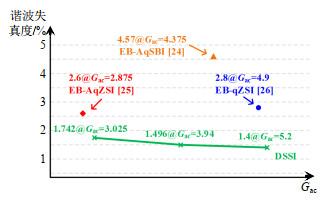
对所提逆变器与现有阻抗源升压逆变器进行输出电压THD仿真比较,比较对象为增强型有源准开关升压逆变器[24](enhanced Boost active quasi switch Boost inverter,EB-AqSBI)、增强型有源准Z源逆变器[25](enhanced Boost active quasi Z source inverter,EB-AqZSI)以及增强型准Z源升压逆变器[26](EB-qZSI),仿真工作条件统一设定为Vin = 36 V、Vo(rms) = 110 V、R = 50 Ω以及交流增益Gac = 3、4、5。仿真结果如图 12所示,由图可知,在3种交流增益条件下,所提逆变器的THD值均低于其他3种阻抗源逆变器,此外,由图可知,由于所提逆变器的输出电压增益可随调制系数的增大而增大,因此所提逆变器的THD值随着交流增益Gac的升高而降低,而阻抗源类型逆变器的调制系数随输出增益的增大而降低,因此其他3种阻抗源逆变器的THD值均随着交流增益Gac的升高而升高,与前述分析吻合。
4.2 实验验证
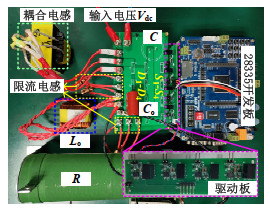
为进一步验证本文所提逆变器的可行性,在实验室搭建1台基于TM320F28335开发板的实验样机,如图 13所示。实验参数设置同仿真设置,如表 2所示。样机所采用的器件型号如表 3所示。
表 3 实验样机参数Table 3. Parameters of the experiment参数 数值 直流母线电容C 860 μF,450 V 耦合电感N1 : N2 : N3 DMR95EE-65B(40 : 60 : 20),Lm = 2 mH 功率开关管S1-S4 60R045P7 二极管D1-D4 RHRG3060 二极管Da-Db RHRG30120 图 14给出所提变换器输入、输出关键波形图,在表 2参数条件下,负载电阻电压UR的有效值约为110 V。负载电阻电流IR的有效值约为2.1 A。
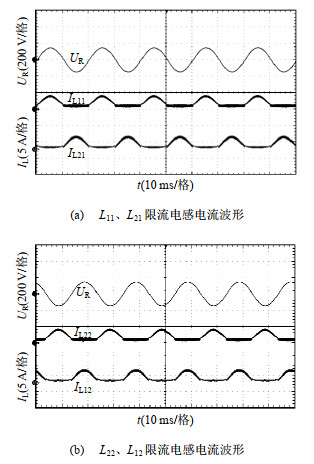
图 15给出DBI结构中4个限流电感的电流波形。从图 15可以看出,连接于同一逆变桥臂的2个限流电感(左侧为L11与L21,右侧为L22与L12)分别在半个工频周期交替流过电流。
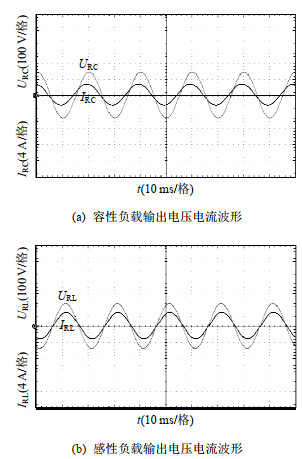
图 16给出所提变换器在不同功率因数负载下的输出电压和电流波形。由图可知,当负载为容性负载时,输出负载R = 50,C = 200 μF,负载阻抗为ZRC = 52.47 ∠ −17.66° Ω,此时输出电流超前输出电压17.66°,如图 16(a)所示。当负载为感性负载时,输出负载R = 50,L = 5 mH,负载阻抗为ZRL = 50.02 ∠ 1.8° Ω,此时输出电流滞后输出电压1.8°,如图 16(b)所示。
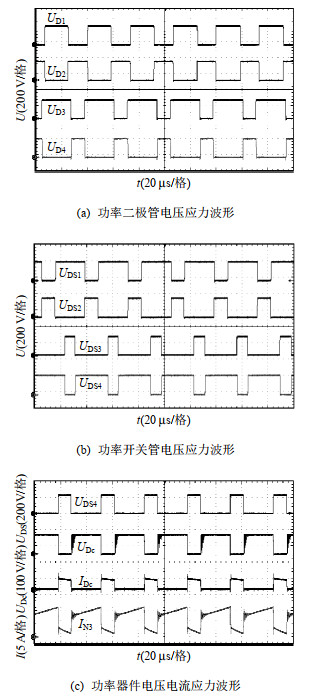
图 17(a)给出DBI中二极管的电压应力波形图,图中DBI二极管的电压应力约为250 V。图 17(b)给出开关管的电压应力波形图,与DBI二极管的电压应力相同,其幅值约为250 V。从图 17(c)可以看出,当开关管S4开通时,流过二极管Dc的电流为零,二极管Dc关断,此时耦合电感N3绕组电流上升,表明此时为耦合电感充电状态,与前述模态分析的导通情况相一致。
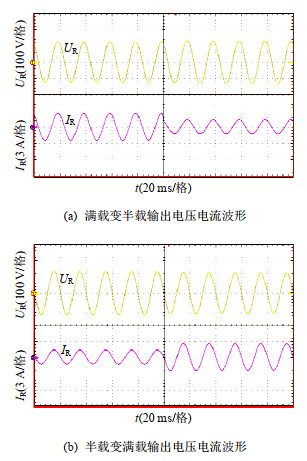
图 18给出所提变换器在负载突变情况下的输出电压电流波形。图 18(a)中,负载由满载(R = 50 Ω)突变至半载(R = 100 Ω),负载电流幅值由满载值降至一半,负载电压幅值则保持稳定;图 18(b)中,负载由半载(R = 100 Ω)突变至满载(R = 50 Ω),负载电流幅值由半载值升至满载值,负载电压幅值则保持稳定,可以看出所提变换器具有良好的动态响应特性。
根据所搭建实验样机的实验数据,在不同调制系数下由YOKOGAWA WT500功率分析仪测出的输出电压THD值如图 19所示,在300 ns死区时间的设置下,3种调制系数下的THD值均在2以下,符合IEEE 519标准。相比于现存其他阻抗源升压逆变器,所提逆变器在不同交流增益下都具有更低的THD值,与前述理论分析和仿真分析相符。
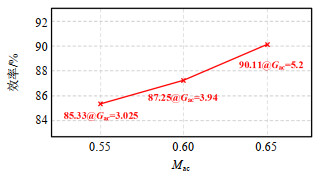
测得不同调制系数下的实验效率如图 20所示,所测出的实验数据与理论仿真数据有少许偏差,这是由于实验采用电路元器件存在的寄生参数导致的。此外,可以通过采用SiC等宽禁带器件代替样机中采用的Si器件,并提高变换器工作频率来减少损耗,提高系统效率。
5. 结论
本文提出了一种单相单级式耦合电感型分裂源升压逆变器及其调制策略,该逆变器具有以下优异特性:
1)高输出电压增益,且输出电压增益调节自由度高;
2)能够有效抑制逆变桥臂直通电流,可靠性高;
3)在高增益条件下仍能保持较高调制系数,保证输出电压波形质量。
本文对该变换器的工作模态、调制策略、输出特性及参数设计进行详尽分析,并搭建一台200 W小功率实验样机。理论分析、仿真结果与实验结果的高度一致性验证该变换器的可行性及有效性。因而,本文所提出的变换器适用于新能源发电领域中高升压逆变需求的单相逆变系统。
-
表 1 功率开关管及二极管电压电流应力
Table 1 Voltage/Current Stresses on Switch and Diode
应力种类 功率开关管 二极管 电压应力 US1 - 4=1+λD1−DUdc {UDa=UDb=1+λD1−DUdcUDc=UC−Udc+UN2UD1=UD2=UD3=UD4=UC 电流应力 {IS1=IS3=IoIS2=IS4=Io+Iin {IDa=IDb=IDc=IinID1=ID2=ID3=ID4=Io 表 2 仿真模型参数
Table 2 Parameters of the simulation
参数 数值 输入电压Udc/V 36 直流母线电容C/μF 860 限流电感L11—L22/μH 100 滤波电感Lo/mH 10 滤波电容Co/μF 3 负载电阻(水泥电阻)Ro/Ω 50 耦合电感匝比N1 : N2 : N3 40 : 60 : 20 励磁电感Lm/mH 2 开关频率fs/kHz 30 调制比Mac 0.65 偏移量Mdc −0.4 表 3 实验样机参数
Table 3 Parameters of the experiment
参数 数值 直流母线电容C 860 μF,450 V 耦合电感N1 : N2 : N3 DMR95EE-65B(40 : 60 : 20),Lm = 2 mH 功率开关管S1-S4 60R045P7 二极管D1-D4 RHRG3060 二极管Da-Db RHRG30120 -
[1] 谭辉, 孔祥福, 曾凡涛. 新能源发电技术研究综述[J]. 山东工业技术, 2014(23): 173-174. https://www.cnki.com.cn/Article/CJFDTOTAL-SDGJ201423150.htm TAN Hui, KONG Xiangfu, ZENG Fantao. Review of new energy power generation technology research[J]. Shandong Industrial Technology, 2014(23): 173-174 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SDGJ201423150.htm
[2] 黄雨涵, 丁涛, 李雨婷, 等. 碳中和背景下能源低碳化技术综述及对新型电力系统发展的启示[J]. 中国电机工程学报, 2021, 41(S1): 28-51. DOI: 10.13334/j.0258-8013.pcsee.211016 HUANG Yuhan, DING Tao, LI Yuting, et al. Decarbonization technologies and inspirations for the development of novel power systems in the context of carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(S1): 28-51 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.211016
[3] 刘永奇, 陈龙翔, 韩小琪. 能源转型下我国新能源替代的关键问题分析[J]. 中国电机工程学报, 2022, 42(2): 515-523. DOI: 10.13334/j.0258-8013.pcsee.210336 LIU Yongqi, CHEN Longxiang, HAN Xiaoqi. The key problem analysis on the alternative new energy under the energy transition[J]. Proceedings of the CSEE, 2022, 42(2): 515-523 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.210336
[4] SHEN Miaosen, JOSEPH A, WANG Jin, et al. Comparison of traditional inverters and Z-source inverter for fuel cell vehicles[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1453-1463. DOI: 10.1109/TPEL.2007.900505
[5] 张一弛, 姚志垒, 毛赛君. 具有电压前馈的两级式逆变器的稳定性分析[J]. 电力电子技术, 2022, 56(3): 105-107, 111. https://www.cnki.com.cn/Article/CJFDTOTAL-DLDZ202203024.htm ZHANG Yichi, YAO Zhilei, MAO Saijun. Stability analysis of two-stage inverter with voltage feedforward[J]. Power Electronics, 2022, 56(3): 105-107, 111 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLDZ202203024.htm
[6] LIU Hongpeng, LOH P C, WANG Xiongfei, et al. Droop control with improved disturbance adaption for a PV system with two power conversion stages[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6073-6085. DOI: 10.1109/TIE.2016.2580525
[7] PENG Fangzheng. Z-source inverter[J]. IEEE Transactions on Industry Applications, 2003, 39(2): 504-510. DOI: 10.1109/TIA.2003.808920
[8] 年珩, 阮晨辉, 何峪嵩, 等. 基于Z源逆变器的共直流母线开绕组永磁同步电机系统控制策略[J]. 中国电机工程学报, 2019, 39(18): 5509-5519. DOI: 10.13334/j.0258-8013.pcsee.181034 NIAN Heng, RUAN Chenhui, HE Yusong, et al. Control strategy for open-winding PMSM system with common DC bus based on Z-source inverters[J]. Proceedings of the CSEE, 2019, 39(18): 5509-5519 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.181034
[9] 张阳, 黄守道, 罗德荣. 一种新型半准Z源逆变器在风力发电变流系统中的应用[J]. 中国电机工程学报, 2017, 37(17): 5107-5117. DOI: 10.13334/j.0258-8013.pcsee.161748 ZHANG Yang, HUANG Shoudao, LUO Derong. A novel half quasi-Z-source inverter for wind energy conversion systems[J]. Proceedings of the CSEE, 2017, 37(17): 5107-5117 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.161748
[10] 吴昊坤, 黄科元, 吕维, 等. 用于高速永磁电机的Z源逆变器直流链电压控制策略[J]. 电工技术学报, 2020, 35(16): 3489-3497. https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202016014.htm WU Haokun, HUANG Keyuan, LÜ Wei, et al. Z-source inverter DC-link voltage control strategy for high speed permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3489-3497 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202016014.htm
[11] 周文齐, 丘东元, 张波, 等. 准开关升压逆变器的多模态组合控制[J]. 中国电机工程学报, 2021, 41(3): 1114-1123. DOI: 10.13334/j.0258-8013.pcsee.200087 ZHOU Wenqi, QIU Dongyuan, ZHANG Bo, et al. Multi-modal combination control of quasi-switched Boost inverter[J]. Proceedings of the CSEE, 2021, 41(3): 1114-1123 (in Chinese). DOI: 10.13334/j.0258-8013.pcsee.200087
[12] CHEN Manxin, YIN Changqing, LOH P C. Magnetically coupled high-voltage-Boost split Y-source inverter without leakage-induced voltage spikes[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5444-5455. DOI: 10.1109/TIE.2019.2931227
[13] ZHU Miao, YU Kun, LUO Fanglin. Switched inductor Z-source inverter[J]. IEEE Transactions on Power Electronics, 2010, 25(8): 2150-2158. DOI: 10.1109/TPEL.2010.2046676
[14] LEE S S. A single-phase single-source 7-level inverter with triple voltage Boosting gain[J]. IEEE Access, 2018, 6: 30005-30011. DOI: 10.1109/ACCESS.2018.2842182
[15] GAJANAYAKE C J, LUO Fanglin, GOOI H B, et al. Extended-boost Z-source inverters[J]. IEEE Transactions on Power Electronics, 2010, 25(10): 2642-2652. DOI: 10.1109/TPEL.2010.2050908
[16] RIBEIRO H, PINTO A, BORGES B. Single-stage DC-AC converter for photovoltaic systems[C]//Proceedings of 2010 IEEE Energy Conversion Congress and Exposition. Atlanta, GA, USA: IEEE, 2010: 604-610.
[17] ABDELHAKIM A, MATTAVELLI P, SPIAZZI G. Three-phase split-source inverter (SSI): analysis and modulation[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7451-7461. DOI: 10.1109/TPEL.2015.2513204
[18] LEE S S, HENG Y E. Improved single-phase split-source inverter with hybrid quasi-sinusoidal and constant PWM[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2024-2031. DOI: 10.1109/TIE.2016.2624724
[19] LEE S S, TAN A S T, ISHAK D, et al. Single-phase simplified split-source inverter (S3I) for Boost DC-AC power conversion[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7643-7652. DOI: 10.1109/TIE.2018.2886801
[20] 房绪鹏, 阚兴宸, 李鑫媛, 等. 一种改进的高增益无电压尖峰分裂Y源逆变器[J]. 电源学报, 2023, 21(5): 41-50. https://www.cnki.com.cn/Article/CJFDTOTAL-DYXB202305006.htm FANG Xupeng, KAN Xingchen, LI Xinyuan, et al. Improved high-gain split Y-source inverter without voltage spikes[J]. Journal of Power Supply, 2023, 21(5): 41-50 (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DYXB202305006.htm
[21] YIN Changqing, DING Wenlong, MING Lei, et al. Single-stage active split-source inverter with high DC-link voltage utilization[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6699-6711. DOI: 10.1109/TPEL.2020.3038688
[22] DABOUR S M, ABDEL-KHALIK A S, AHMED S, et al. An optimal PWM technique for dual-output nine-switch Boost inverters with minimum passive component count[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 1065-1079. DOI: 10.1109/TPEL.2020.3001372
[23] HU Haibing, HARB S, KUTKUT N, et al. A review of power decoupling techniques for microinverters with three different decoupling capacitor locations in PV systems[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2711-2726. DOI: 10.1109/TPEL.2012.2221482
[24] ZHU Xiaoquan, YE Kaiwen, JIANG Liming, et al. Nonisolated single-phase quadratic switched-Boost inverter with continuous input current and step-up inversion capability[J]. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 2023, 4(1): 276-287. DOI: 10.1109/JESTIE.2022.3214153
[25] GU Yuanwei, CHEN Yanfeng, ZHANG Bo. Enhanced-Boost quasi-Z-source inverter with an active switched Z-network[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 8372-8381. DOI: 10.1109/TIE.2017.2786214
[26] JAGAN V, KOTTURU J, DAS S. Enhanced-Boost quasi-Z-source inverters with two-switched impedance networks[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 6885-6897. DOI: 10.1109/TIE.2017.2688964
-
期刊类型引用(0)
其他类型引用(1)




 下载:
下载:

 下载:
下载:



