Definition and Index of Short Circuit Ratio for Multiple Renewable Energy Stations
-
摘要: 随着新能源在电力系统中占比不断增加、接入形式的多样化，局部地区出现了新能源并入弱交流电网的场景，这是出现宽频带振荡、过电压等问题的影响因素之一，因此，亟需提出理论科学、工程实用的新能源接入规模的量化评估指标。该文首先基于短路比的物理本质，提出计及场站间相互影响的新能源多场站短路比(multiple renewable energy stations short circuit ratio，MRSCR)定义及计算方法，并根据系统阻抗比与短路比间的关联关系，给出针对不同阻抗比范围的计算解析表达式。其次，对新能源多场站临界短路比进行定性分析，并基于典型电网参数计算结果从工程应用的角度提出MRSCR临界指标。最后，依托电力系统分析综合程序(power system analysis synthesis program，PSASP)开发MRSCR计算模块，通过时域仿真算例验证所提出MRSCR对多新能源场站接入系统电压强度表征作用的有效性。
-
关键词:
- 多新能源场站接入系统 /
- 新能源多场站短路比 /
- 阻抗比 /
- 系统电压强度 /
- 新能源接入规模
Abstract: As the scale of renewable energy integration in the power system continues to increase, the scenario of renewable energy stations connected to weak AC grid appears in some local areas, giving rise to broad-band oscillation or overvoltage, which restricts the security and stability operation of power system. Aiming at determining the scale of renewable energy integration, it is of great urgence to propose a quantitative index which possess solid theoretically foundation as well as practical engineering background. In this regard, firstly, based on the physical meaning of short circuit ratio, considering mutual influence of multiple renewable energy stations, the definition and calculation method of multiple renewable energy stations short circuit ratio (MRSCR) was proposed. Calculation formulas for different application scenarios were derived according to the correlation between system impedance ratio and short circuit ratio. In what follows, a qualitative analysis of the critical index of MRSCR was carried out, and the critical MRSCR index was proposed through calculation with practical power system parameters. Finally, the MRSCR calculation module was developed based on PSASP, and time-domain simulation was carried out, which verified the effectiveness of the proposed MRSCR and its critical index for the indication of the power system voltage strength. -
0. 引言
近年来，我国电网中以风电、光伏为代表的新能源发电设备大规模接入[1]，现有新能源发电设备大多采用跟踪电网电压的控制模式，需要交流电网提供电压支撑[2-4]。随着新能源在系统中占比的不断增加，局部地区出现了新能源并入弱交流电网的场景，这是出现宽频带振荡、过电压等问题的因素之一[5-6]。目前，国家强制性标准GB38755-2019《电力系统安全稳定导则》明确要求新能源场站短路比应达到合理水平[7-8]，因此，亟需提出理论科学、工程实用的新能源场站短路比指标，直观有效地衡量多新能源场站接入系统电压强度，进而对新能源接入规模进行量化评估。
电力系统网络某点的短路容量等于该点三相短路电流与额定电压的乘积，是系统电压强度的标志[9]。系统短路容量与电气设备(含电力电子设备)容量间的比值即为短路比(short circuit ratio，SCR)。长期以来，短路比作为一种静态分析方法，以其简单性、直观性，为电网的规划和运行提供了重要的参考依据[10]。为了评价多回直流同时馈入交流电网的电压强度，国际大电网组织(CIGRE)提出了基于多馈入相互作用因子的多馈入短路比(multi-infeed short circuit ratio，MISCR)[11]。文献[12]基于解耦方法，提出了广义短路比指标，进一步明确传统直流短路比在多馈入场景下的物理机理。与常规直流特性明显不同，新能源发电设备除传输有功外，还可以向交流电网提供无功支撑。在多新能源场站接入系统电压强度评价指标方面，基于传统直流短路比，文献[13-14]分别提出了加权短路比(weighted short circuit ratio，WSCR)及复合短路比(composite short circuit ratio，CSCR)。但上述基于SCR的系统电压强度评价方法假设所有电力电子设备都连接在同一交流落点，不能反映新能源多场站间交互作用对系统电压强度的影响的物理特性。为此，CIGRE B4.62工作组提出可采用类似多馈入直流的等效短路比(equivalent short circuit ratio，ESCR)评估新能源场站并网点强度[15]，在此基础上，文献[16]提出了场站位置相关短路比(site-dependent short circuit ratio，SDSCR)，并基于静态电压稳定裕度对系统电压强度进行分析。
多新能源场站接入系统与多直流馈入系统的短路比计算存在较大差别。首先，多馈入直流短路比计算中关注的直流接入点大多为换流站交流母线，落点较少且电压等级较高; 其次，多新能源场站接入系统实际运行中，新能源场站需要提供无功功率用以补偿新能源场站内集电线、站外送出线路的部分无功损耗[17]; 最后，覆盖范围较大的多个新能源场站并网时，各场站并网点母线节点间阻抗角及初始相位角均可能存在较大差异。然而，上述已有多新能源场站接入系统的电压强度评估方法均沿用了传统直流短路比中忽略了系统等值阻抗电阻部分影响及各场站之间电压相角相同的假设，无法反映新能源发电设备的无功输出、新能源场站内不同节点之间各电气量幅值、相位差的区别。
为此，本文基于电力系统短路比的物理本质，给出计及多新能源场站间相互影响的新能源多场站短路比(multiple renewable energy station short circuit ratio，MRSCR)定义，在放开传统CIGRE短路比推导所有假设后，提出更为详细和完备的MRSCR计算公式，考虑了不同节点之间各电气量幅值、相位差，并可计及新能源发电设备无功的影响，适用于各类不同场景下多新能源场站接入系统电压强度评估计算。在此基础上进一步根据系统等值阻抗${\dot Z_{{\text{eq}}}} = R + {\text{j}}X$的阻抗比X/R大小，考虑各场站之间电压相角相近的假设条件，原有短路比计算公式可继续沿用，与传统MISCR具有同样形式。通过典型电网参数折算，提出评价多新能源场站接入交流系统电压强度的MRSCR临界指标。最后，依托电力系统分析综合程序(power system analysis synthesis program，PSASP)开发MRSCR计算模块，计算我国某直流送端系统各新能源场站的MRSCR，并通过时域仿真验证所提出MRSCR及其临界指标对多新能源场站接入系统电压强度指征作用的有效性。
1. 新能源多场站短路比(MRSCR)
1.1 MRSCR定义及表达式
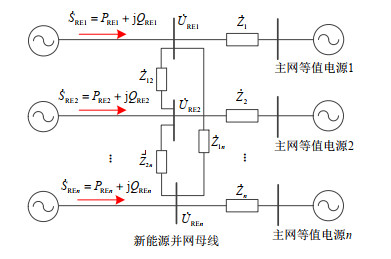
戴维南等值方法可将新能源接入的交流系统简化为一个理想电压源串联等值阻抗。利用多端口戴维南等值，可以得到图 1所示的i(i=1, 2, …, n)个新能源场站同时接入交流系统的简化等值模型示意图。
![]()
图 1 多新能源场站接入的交流系统简化模型Figure 1. Simplified model of AC system connected with multiple renewable energy stations图 1中${\dot S_{{\text{RE}}i}}$，${P_{{\text{RE}}i}}$，${Q_{{\text{RE}}i}}$和${\dot U_{{\text{RE}}i}}$分别为新能源发电设备/场站i的视在功率、有功功率、无功功率和并网母线电压，${\dot Z_{ij}}$为折算的并网点i、j间等值阻抗，${\dot Z_i}$为主网等值电源i与对应并网点间的系统侧折算等值阻抗。
图 1中新能源并网母线可分别表示新能源发电设备电网侧接入点或新能源场站并网点(新能源场站升压站高压侧母线或节点[17])。设各新能源并网母线注入交流系统的电流分别为${\dot I_1}$, ${\dot I_2}$, …, ${\dot I_n}$，则各并网母线节点电压${\dot U_{{\text{RE}}1}}$, ${\dot U_{{\text{RE}}2}}$, …, ${\dot U_{{\text{RE}}n}}$可表示为
$$\left[ {\begin{array}{*{20}{c}} {{{\dot U}_{{\text{RE}}1}}} \\ {{{\dot U}_{{\text{RE}}2}}} \\ \vdots \\ {{{\dot U}_{{\text{RE}}n}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\dot Z}_{{\text{eq}}11}}}&{{{\dot Z}_{{\text{eq}}12}}}& \cdots &{{{\dot Z}_{{\text{eq}}1n}}} \\ {{{\dot Z}_{{\text{eq}}21}}}&{{{\dot Z}_{{\text{eq}}22}}}& \cdots &{{{\dot Z}_{{\text{eq}}2n}}} \\ \vdots & \vdots &{}& \vdots \\ {{{\dot Z}_{{\text{eq}}n1}}}&{{{\dot Z}_{{\text{eq}}n2}}}& \cdots &{{{\dot Z}_{{\text{eq}}nn}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot I}_1}} \\ {{{\dot I}_2}} \\ \vdots \\ {{{\dot I}_n}} \end{array}} \right]$$ (1) 式中${\dot Z_{{\text{eq}}ij}}$为新能源并网母线处的交流电网等值阻抗矩阵Zeq的第i行、j列元素。注意，图 1中的${\dot Z_{ij}}$和${\dot Z_n}$仅用于示意，与${\dot Z_{{\text{eq}}ij}}$间并无实际对应关系。
短路比用于衡量设备接入系统后，系统标称电压与设备产生电压之间的相对大小[9]。基于上述物理意义，系统中第i个新能源并网母线处的MRSCR为
$${\text{MRSC}}{{\text{R}}_i} = \frac{{\left| {{{\dot U}_{{\text{N}}i}}} \right|}}{{\left| {{{\dot U}_{{\text{RE}}i}}} \right|}} = \frac{{\left| {{{\dot U}_{{\text{N}}i}}} \right|}}{{\left| {{{\dot Z}_{{\text{eq}}ii}}{{\dot I}_i} + \sum\limits_{j = 1, j \ne i}^n {{{\dot Z}_{{\text{eq}}ij}}{{\dot I}_j}} } \right|}}$$ (2) 式中：${\dot U_{{\text{N}}i}}$为第i个并网母线节点标称电压; ${\dot U_{{\text{RE}}i}}$为设备(新能源)发电功率在第i个节点上产生的电压，下标RE表示新能源发电设备/场站; ${\dot I_i}$为第i个新能源发电设备/场站提供的短路电流。令第i个并网母线节点的实际运行电压为${\dot U_i}$，将式(2)分子分母同乘以$\left| {\dot U_i^*{\text{/}}{{\dot Z}_{{\text{eq}}ii}}} \right|$可得：
$$\begin{gathered} {\text{MRSC}}{{\text{R}}_i}{\text{ = }}\frac{{\left| {{{\dot U}_i}^*{{\dot U}_{{\text{N}}i}}/{{\dot Z}_{{\text{eq}}ii}}} \right|}}{{\left| {{{\dot U}_i}^*{{\dot I}_i} + \sum\limits_{j = 1, j \ne i}^n {\frac{{{{\dot Z}_{{\text{eq}}ij}}}}{{{{\dot Z}_{{\text{eq}}ii}}}}\dot U_i^*{{\dot I}_j}} } \right|}} = \\ {\text{ }}\left| {\frac{{\dot U_i^*{{\dot U}_{{\text{N}}i}}}}{{{{\dot Z}_{{\text{eq}}ii}}}}} \right|/\left| {{{\dot S}_{{\text{RE}}i}} + \sum\limits_{j = 1, j \ne i}^n {{{\dot \Pi }_{ij}}{{\dot S}_{{\text{RE}}j}}} } \right| \\ \end{gathered} $$ (3) 式中：${\dot S_{{\text{RE}}i}}$为第i个新能源并网母线节点注入的新能源实际视在功率; ${\dot \Pi _{ij}} = {\dot Z_{{\text{eq}}ij}}\dot U_i^*{\text{/}}{\dot Z_{{\text{eq}}ii}}\dot U_j^*$为新能源并网母线i和j之间的复数功率折算因子，反映了各新能源发电设备电网侧接入点/新能源场站并网点电气量之间相位和幅值差异。
根据实际需要，根据式(3)可分别计算得到新能源发电设备电网侧接入点(通常为690V/400V)的MRSCRG，或是新能源场站并网点(电压等级根据各电网具体情况有所不同，通常为110kV/220kV/ 330kV母线)的MRSCRS。
由式(3)可知，当仅考虑单个新能源发电设备/场站接入交流系统时，相应的新能源场站短路比(renewable energy station short circuit ratio，RSCR)定义为
$${\text{RSCR}} = \left| {{{\dot U}^*}{{\dot U}_{\text{N}}}/{{\dot Z}_{{\text{eq}}}}} \right|/\left| {{{\dot S}_{{\text{RE}}}}} \right|$$ (4) 式中${\dot Z_{{\text{eq}}}} = R + {\text{j}}X$为从新能源发电设备电网侧接入点/新能源场站并网点的系统侧等值阻抗。
当满足CIGRE指标的系列假设条件[15]，并分别取新能源并网母线额定电压和新能源发电功率为电压基准值和功率基准值，式(4)定义的RSCR与传统SCR[19]具有同样的形式：
$${\text{RSCR}} = \frac{{{S_{{\text{ac}}}}}}{{{P_{{\text{RE}}}}}} = \frac{1}{{{{\left| {\dot Z} \right|}_{{\text{pu}}}}}}$$ (5) 式中：Sac和${P_{{\text{RE}}}}$分别为新能源发电设备电网侧接入点/场站并网点的三相短路容量及注入的有功功率; ${\left| {\dot Z} \right|_{{\text{pu}}}}$为交流系统等效电抗标幺值。
1.2 阻抗比(X/R)对短路比(RSCR)的影响
实际生产运行中，新能源场站通常接入较低电压等级电网，当新能源场站覆盖范围较大时，各场站节点系统侧等值阻抗${\dot Z_{{\text{eq}}}} = R + {\text{j}}X$的阻抗比X/R及阻抗角$\varphi = \arctan (X{\text{/}}R)$可能根据接入点的电压等级不同存在较大差异[18]。传统短路比仅考虑了交流系统等值阻抗幅值大小，并未考虑阻抗比X/R及阻抗角$\varphi $的影响。
然而，系统的最大传输功率与短路比和交流系统阻抗角$\varphi $有关。以发生短路故障为例，新能源场站接入系统的等值阻抗将发生变化，故障不仅会导致电压下降，还会导致电压相角的变化，这种现象通常称为“相角跃变”，导致新能源发电设备的锁相环节无法正确跟踪电压。大的相角跃变可能导致暂态电流较高，并导致锁相环无法正确跟踪电压，进而影响其故障穿越能力。对于同步发电机，电压相位与转子位置强耦合变化缓慢，因而通常不需要考虑相角跃变; 对于使用锁相环的风电场、光伏电站，母线电压相位与转子位置无关，相角跃变对暂态特性有明显影响[18]。因此，对于多新能源场站接入系统来说，通常将短路比作为主要指标，将X/R作为辅助指标，帮助评估交流系统的电压强度。
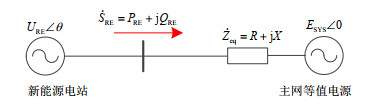
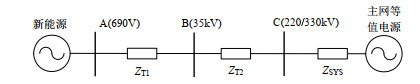
下面以图 2所示的新能源场站接入系统为例，分析阻抗比X/R对短路比RSCR的影响。
![]()
图 2 新能源场站接入系统等效电路Figure 2. Equivalent circuit of AC system connected with a renewable energy station图 2中，URE和$ \theta $分别为新能源发电设备电网侧接入点/场站并网点母线电压的幅值和相角，${\dot S_{{\text{RE}}}}$、PRE和QRE分别为新能源注入的视在功率、有功功率和无功功率。ESYS为主网等值电源幅值，${\dot Z_{{\text{eq}}}}$为新能源和主网等值电源间的等值阻抗。图 2所示系统的潮流方程为
$$\begin{gathered} {{\dot S}_{{\text{RE}}}} = {P_{{\text{RE}}}} + {\text{j}}{Q_{{\text{RE}}}} = ({U_{{\text{RE}}}}\cos \theta + {\text{j}}{U_{{\text{RE}}}}\sin \theta ) \cdot \\ {\text{ }}{(\frac{{{U_{{\text{RE}}}}\cos \theta + {\text{j}}{U_{{\text{RE}}}}\sin \theta - {E_{{\text{SYS}}}}}}{{R + {\text{j}}X}})^ * } \\ \end{gathered} $$ (6) 当系统发生电压崩溃时，根据以公式(6)中${U_{{\text{RE}}}}$为自变量的一元二次方程的判别式等于0可推导出式(5)中的RSCR与X/R的关系为
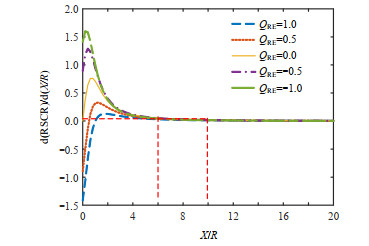
$$\begin{gathered} {\text{RSCR}} = \frac{{2{{(\frac{X}{R}{P_{{\text{RE}}}} - {Q_{{\text{RE}}}})}^2}}}{{\sqrt {P_{{\text{RE}}}^{\text{2}} + Q_{{\text{RE}}}^{\text{2}}} \sqrt {1 + {{(X{\text{/}}R)}^2}} }} \cdot \\ {\text{ }}\frac{1}{{(X{\text{/}}R \times {Q_{{\text{RE}}}} + {P_{{\text{RE}}}}) + \sqrt {P_{{\text{RE}}}^{\text{2}} + Q_{{\text{RE}}}^{\text{2}}} \sqrt {1 + {{(X{\text{/}}R)}^2}} }} \\ \end{gathered} $$ (7) 根据式(7)，固定${P_{{\text{RE}}}}{\text{ = }}1$，在${Q_{{\text{RE}}}}$不同取值下RSCR对X/R的导数与X/R之间的关系如图 3所示。
![]()
图 3 不同QRE取值下RSCR对X/R的导数Figure 3. The derivative of RSCR to X/R versus X/R with different QRE从图 3中可以看出，系统等值阻抗${\dot Z_{{\text{eq}}}} = R + {\text{j}}X$的阻抗比X/R > 10时，X/R对短路比RSCR的影响小于1%，在工程计算时可以忽略系统等值阻抗中电阻部分的影响。
1.3 基于X/R的MRSCR表达式
由式(3)-(4)可知，RSCR是MRSCR的特殊形式，X/R对RSCR的影响同样适用于MRSCR。下面进一步根据1.2节得到的X/R与MRSCR之间的关系，确定不同条件下的MRSCR表达形式。当计算新能源发电设备电网侧接入点的MRSCRG时，由于通常无法满足X/R > 10的条件，因此计算时需要采用复数形式，即式(3);当计算新能源场站并网点MRSCRS时，如果满足X/R > 10且假设各场站之间电压相角相近时，则式(3)可简化为
$${\text{MRSC}}{{\text{R}}_i} = \frac{{{S_{{\text{ac}}i}}}}{{{P_{{\text{RE}}i}} + \sum\limits_{j \in i, j \ne i}^n {\left| {\frac{{{Z_{{\text{eq}}ij}}{U_i}}}{{{Z_{{\text{eq}}ii}}{U_j}}}} \right|} {P_{{\text{RE}}j}}}}$$ (8) 若进一步考虑$\left| {{U_i}} \right| = \left| {{U_j}} \right| = 1$，则有：
$${\text{MRSC}}{{\text{R}}_i} = {S_{{\text{ac}}i}}/({P_{{\text{RE}}i}} + \sum\limits_{j \in i, j \ne i}^n {\lambda {}_{ij}} {P_{{\text{RE}}j}})$$ (9) 式中${\lambda _{ij}} = \left| {{Z_{{\text{eq}}ij}}/{Z_{{\text{eq}}ii}}} \right|$是新能源并网母线i和j之间的功率折算因子，反映了各新能源发电设备电网侧接入点/新能源场站并网点等值阻抗的幅值差异。不难看出，式(9)中的MRSCR与CIGRE提出的传统直流多馈入短路比MISCR具有类似形式。对比公式(6)和(9)可知，多新能源场站接入情况下，由于考虑了各新能源场站间的相互影响，对统一接入点来说，MRSCR指标相对保守，其数值比RSCR偏小。
综上，系统中新能源发电设备电网侧接入点/场站并网母线节点i的新能源多场站短路比MRSCRi可表示为
$$ \begin{array}{l}{\text{MRSCR}}_{i}=\\ \left\{ \begin{array}{l}\frac{\left|{\dot{U}}_{i}^{*}{\dot{U}}_{\text{N}i}/{\dot{Z}}_{\text{eq}ii}\right|}{\left|{\dot{S}}_{\text{RE}i}+{\displaystyle \sum _{j=1, j\ne i}^{n}{\dot{\Pi }}_{ij}{\dot{S}}_{\text{RE}j}}\right|}, \frac{X}{R}<10 \\ \frac{{S}_{\text{ac}i}}{{P}_{\text{RE}i}+{\displaystyle \sum _{j\in i, j\ne i}^{n}\lambda {}_{ij}}{P}_{\text{RE}j}}, \frac{X}{R}\ge 10且\left|{U}_{i}\right|=\left|{U}_{j}\right|=1 \end{array} \right.\end{array}$$ (10) 与传统多馈入直流短路比类似，新能源多场站短路比反映了多新能源场站接入系统的电压强度及电网对新能源发电设备电网侧接入点/场站并网点母线无功电压支撑能力的大小。
2. 新能源场站临界短路比
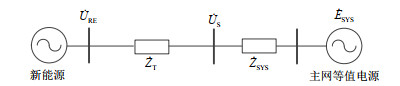
在图 2基础上，进一步考虑新能源场站内升压变压器等值阻抗后的等效电路如图 4所示。
![]()
图 4 新能源发电设备经变压器接入系统等效电路Figure 4. Equivalent circuit of AC system connected with a renewable energy station through a transformer图 4中，${\dot U_{{\text{RE}}}}$为新能源发电设备电网侧接入点交流母线电压，${\dot U_{\text{S}}}$为场站并网点母线电压，${\dot E_{{\text{SYS}}}}$为交流系统侧等效电压，${\dot Z_{\text{T}}}$为变压器及线路等效阻抗，${\dot Z_{{\text{SYS}}}}$为交流系统戴维南等值阻抗。单位电压下新能源发电设备电网侧接入点短路比RSCRG与新能源场站并网点短路比之间RSCRS具有以下关系：
$$\frac{1}{{{\text{RSC}}{{\text{R}}_{\text{G}}}}} = \frac{1}{{{\text{RSC}}{{\text{R}}_{\text{S}}}}} + \left| {{{\dot Z}_{\text{T}}}} \right|$$ (11) 经单个发电设备并网系统的电磁暂态仿真测试，不同新能源并网逆变器的新能源发电设备电网侧接入点短路比RSCRG在1.1~1.8之间时，会出现临界不稳定现象。近年来，结合运行实际，国内外对接入弱系统的新能源发电设备性能提出了要求[20-22]。其中，澳大利亚电网要求任何发电设备均需在接入点短路比为1.5的系统条件下能够稳定运行[21]，华为对此进行了测试验证[22]。因此，本文从工程实际需求角度，选取系统中新能源发电设备接入点处的RSCRG=1.5作为基本运行条件。进一步，考虑新能源发电设备电网侧接入点短路比为RSCRG=2时，可保证不同性能新能源发电设备的并网稳定性，所接入的交流系统属于较强系统水平。
本节基于我国各大区电网中不同的新能源并网典型接线情况统计，以实际电网中几种典型场站升压结构为例，分别求取相应的新能源场站并网点的临界短路比。
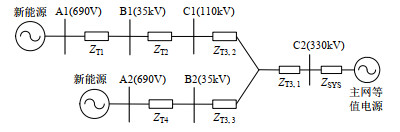
1) 新能源发电设备经两绕组变压器升压至并网点，分别考虑两类典型330kV/35kV/690V及220kV/35kV/690V两绕组变压器升压方式，如图 5所示。
![]()
图 5 风机经两绕组变压器升压至场站并网点Figure 5. Renewable energy stations connected to the grid connected point through a two-winding transformer图 5中${\dot Z_{{\text{T1}}}}$和${\dot Z_{{\text{T3}}}}$分别为两绕组升压变压器阻抗。当新能源发电设备电网侧接入点母线A处的短路比满足RSCRG=1.5基本运行条件时，根据实际电网参数，经式(11)对母线C处新能源场站并网点的临界短路比RSCRS的折算结果见表 1中算例1~4。
表 1 新能源场站并网点C的RSCRSTable 1. RSCRS of the grid connection point C算例 ${\dot Z_{{\text{T1}}}}$(折算值) ${\dot Z_{{\text{T3}}}}$(折算值) 场站短路比RSCRS 1 j0.0304 j0.0604 1.737(330kV) 2 j0.0650 0.0008+j0.0565 1.84(330kV) 3 j0.0619 j0.1022 1.99(220kV) 4 j0.0406 j0.0766 1.819(220kV) 2) 新能源发电设备经三绕组变压器升压至并网点，如图 6所示。
![]()
图 6 新能源经三绕组变压器升压至并网点Figure 6. Renewable energy stations connected to the grid connected point through a three-winding transformer图 6中${\dot Z_{{\text{T1}}}}$和${\dot Z_{{\text{T4}}}}$为35kV/0.69kV两绕组升压变压器阻抗，${\dot Z_{{\text{T2}}}}$为110kV/35kV两绕组升压变阻抗，${\dot Z_{{\text{T3, 1}}}}$、${\dot Z_{{\text{T3, 2}}}}$、${\dot Z_{{\text{T3, 3}}}}$分别为330kV/110kV/35kV三绕组升压变的高压、中压及低压侧阻抗。考虑当新能源发电设备电网侧接入点母线A1及A2处的短路比RSCRG=1.5时，经公式(11)折算，可得经过典型110kV/35kV两绕组变压器低压侧接入系统母线C1处新能源场站并网点短路比临界值RSCRS1=2.134，如表 2中算例5所示; 算例6~7不同电网参数下，经典型330kV/ 110kV/35kV三绕组变压器低压侧接入系统母线C2处新能源场站并网点的临界短路比RSCRS2计算结果见表 3。
表 2 新能源场站并网点C1(110kV)的RSCRS1Table 2. RSCRS1 of the grid connection point C1算例 ${\dot Z_{{\text{T1}}}}$(折算值) ${\dot Z_{{\text{T2}}}}$(折算值) 场站短路比RSCRS1 5 0.000370+j0.093000 0.002141+j0.105 2.134 表 3 新能源场站并网点C2(330kV)的RSCRS2Table 3. RSCRS2 of the grid connection point C2算例 ${\dot Z_{{\text{T4}}}}$(折算值) ${\dot Z_{{\text{T3, 1}}}}$(折算值) ${\dot Z_{{\text{T3, 3}}}}$(折算值) 场站短路比RSCRS2 6 j0.0495 0.0003-j0.0043 0.0002+j0.0332 1.725 7 0.000370+ j0.093000 0.000256+ j0.031333 0.000904+ j0.038556 1.985 由表 1-3中计算结果可知，当新能源发电设备电网侧接入点处RSCRG满足1.5的基本运行条件时，考虑如表 1-3所示的实际电网典型参数，折算到新能源场站并网点处的RSCRS范围在1.7~2.1之间。进一步结合式(6)和(9)，若新能源场站并网点的新能源多场站短路比MRSCRS在1.7~2.1之间，即可满足该新能源场站所接入新能源发电设备的正常运行需求。进一步结合大量仿真算例验证，保留一定工程裕度，推荐新能源场站并网点的临界短路比MRSCRS取为2.0~2.5。同理，若考虑RSCRG=2，所接入的交流系统属于较强系统水平，折算到新能源场站并网点处的短路比范围在2.5~3.3之间，相应的新能源场站并网点临界短路比MRSCRS可取为3.0~3.5。若满足MRSCRS > 3.5，则交流系统电压强度具有较大裕度。
3. 仿真验证
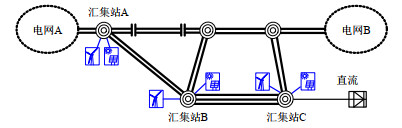
本节以如图 7所示的某直流送端电网为例进行时域仿真验证。初始方式下系统中无调相机接入，通过A、B和C三个汇集站汇入交流电网的新能源总出力12500MW。
基于本文所提出的MRSCR指标，在中国电科院自主研发的PSASP中开发了新能源场站短路比PSASP-MRSCR计算模块。在初始方式基础上，进一步考虑在各新能源场站并网点配置分布式调相机的运行方式。基于该模块计算得到不同调相机配置下的场站并网点MRSCRS结果如表 4所示。
表 4 不同调相机配置下新能源场站并网点MRSCRSTable 4. MRSCRS of the grid connection point with different synchronous condenser configurations新能源场站并网点 初始方式无调相机 加装调相机 并网点1 2.41 3.28 并网点2 2.37 3.23 并网点3 2.08 2.86 并网点4 2.05 2.84 并网点5 1.96 2.58 并网点6 1.84 2.40 并网点7 1.97 2.69 并网点8 1.92 2.62 并网点9 2.08 2.92 并网点10 1.83 2.51 并网点11 1.99 2.78 并网点12 2.12 3.02 由表 4结果可知，初始无调相机方式下各新能源场站并网点的MRSCRS最低值为1.83，不满足本文推荐新能源场站并网点MRSCRS临界指标要求。通过在并网点加装调相机，从各新能源场站并网点母线看进去的等值节点阻抗矩阵Zeq变小，由式(10)可知各场站并网点母线MRSCRS增大。由表 4中计算结果可知，加装调相机后，MRSCRS最低值为2.51，大于2.0~2.5的临界指标要求。
初始方式下各汇集站所接入新能源发电设备电网侧接入点处MRSCRG最高/最低值如表 5所示。
表 5 初始无调相机方式下新能源机端MRSCRGTable 5. MRSCRG of the invertor terminal without synchronous condenser新能源汇集站 新能源发电设备 机端母线MRSCRG 汇集站A 新能源1 1.61 新能源2 1.28 汇集站B 新能源3 1.34 新能源4 1.12 汇集站C 新能源5 1.82 新能源6 1.20 由表 5结果可知，初始无调相机时新能源发电设备电网侧接入点处MRSCRG最低值为1.12，同样不满足基本运行条件。
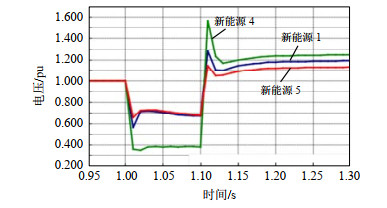
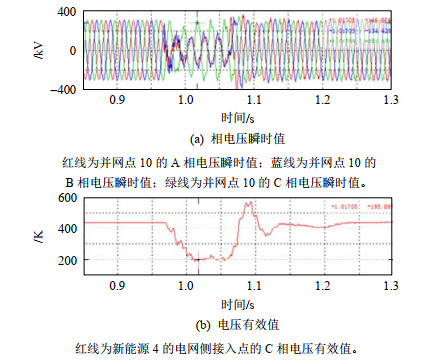
此外，电网故障扰动期间的过电压水平与新能源多场站短路比密切相关。基于PSASP机电暂态仿真程序，对不同新能源发电设备电网侧接入点处的MRSCRG与故障扰动期间新能源机端的过电压关系进行仿真研究。其中，汇集站B处发生某交流线路故障期间各新能源发电设备机端电压如图 8所示。由图 8可知，新能源4的机端过电压最高为1.564pu; 新能源1的机端过电压为1.284pu; 新能源5的机端过电压较小为1.144pu。
![]()
图 8 不同短路比下的新能源机组过电压Figure 8. Comparison of overvoltage of renewable energy with different MRSCR过电压与故障冲击大小、短路容量水平均有关系。结合表 5结果可知，相同条件下，新能源发电设备电网侧接入点处短路比越小，故障扰动期间该新能源发电设备机端过电压越高，反之若新能源发电设备电网侧接入点处越大，过电压越低。
进一步通过基于全电磁暂态仿真对上述结果进行验证。如图 9所示，初始无调相机运行方式下，由于新能源多场站短路比未达到临界指标要求，扰动后系统中新能源机端电气量持续发生不稳定振荡现象。
![]()
图 9 初始无调相机方式下电磁暂态仿真曲线Figure 9. Electromagnetic transient simulation result without synchronous condenser图 9所示仿真结果表明，在系统新能源多场站短路比MRSCR较低时，交流系统电压支撑能力不足，可能是引起振荡失稳现象的原因之一。关于故障后发生持续变化振荡的原因，将结合后续由电网谐振特性主导的振荡等相关评估指标开展进行持续深入研究。根据表 4计算结果，通过加装调相机增大系统各并网点母线MRSCRS，在相同的新能源发电设备模型及控制参数下，电磁暂态初始工况下的失稳现象得到了抑制，如图 10所示。
![]()
图 10 加装分布式调相机方式电磁暂态仿真曲线Figure 10. Electromagnetic transient simulation with distributed synchronous condensers上述仿真结果表明，MRSCR对于多新能源场站接入的交流系统的电压强度具有较好的指征能力，验证了文中提出的MRSCR临界指标的有效性。
4. 结论及建议
本文提出了新能源多场站短路比MRSCR定义及具备工程实用意义的临界指标，通过自主产权仿真软件PSASP中所开发的计算模块，计算得到了新能源场站MRSCR，并通过时域仿真结果验证了所提出MRSCR及其临界指标对多新能源场站接入系统电压强度指征作用有效性。具体结论如下：
1) 衡量系统与所接入新能源发电之间相对强弱时，传统短路比仅考虑了交流系统戴维南等值阻抗幅值大小，并未考虑阻抗角的影响。本文所提出的MRSCR计算公式，可考虑不同节点之间各电气量幅值、相位差，计及新能源发电设备无功的影响，适用于各类不同场景下多新能源场站接入系统电压强度评估计算。
2) 推导了系统等值阻抗${\dot Z_{{\text{eq}}}} = R + {\text{j}}X$的阻抗比X/R与短路比之间的关系，进一步根据不同的X/R取值范围，考虑各场站之间电压相角相近的假设条件，原有短路比计算公式可继续沿用。通过典型电网参数折算，从工程应用角度提出了评价多新能源场站接入交流系统相对强弱的MRSCR临界值取值范围。
3) 本文提出的MRSCR指标本质上是考虑了新能源多场站关联关系的系统短路容量与新能源容量视在功率的比值，该指标能够在一定程度上反映系统的相对电压强度水平。由于短路比分析指标是一种潮流分析模型的解析表达，无法表征分析系统及新能源发电设备的动态控制特性，根据具体情况需进一步开展大电网时域仿真分析研究。
-
![]()
图 1 多新能源场站接入的交流系统简化模型
Figure 1. Simplified model of AC system connected with multiple renewable energy stations
![]()
图 2 新能源场站接入系统等效电路
Figure 2. Equivalent circuit of AC system connected with a renewable energy station
![]()
图 3 不同QRE取值下RSCR对X/R的导数
Figure 3. The derivative of RSCR to X/R versus X/R with different QRE
![]()
图 4 新能源发电设备经变压器接入系统等效电路
Figure 4. Equivalent circuit of AC system connected with a renewable energy station through a transformer
![]()
图 5 风机经两绕组变压器升压至场站并网点
Figure 5. Renewable energy stations connected to the grid connected point through a two-winding transformer
![]()
图 6 新能源经三绕组变压器升压至并网点
Figure 6. Renewable energy stations connected to the grid connected point through a three-winding transformer
![]()
图 8 不同短路比下的新能源机组过电压
Figure 8. Comparison of overvoltage of renewable energy with different MRSCR
![]()
图 9 初始无调相机方式下电磁暂态仿真曲线
Figure 9. Electromagnetic transient simulation result without synchronous condenser
![]()
图 10 加装分布式调相机方式电磁暂态仿真曲线
Figure 10. Electromagnetic transient simulation with distributed synchronous condensers
表 1 新能源场站并网点C的RSCRS
Table 1 RSCRS of the grid connection point C
算例 ˙ZT1(折算值) ˙ZT3(折算值) 场站短路比RSCRS 1 j0.0304 j0.0604 1.737(330kV) 2 j0.0650 0.0008+j0.0565 1.84(330kV) 3 j0.0619 j0.1022 1.99(220kV) 4 j0.0406 j0.0766 1.819(220kV) 
下载: 导出CSV
表 2 新能源场站并网点C1(110kV)的RSCRS1
Table 2 RSCRS1 of the grid connection point C1
算例 ˙ZT1(折算值) ˙ZT2(折算值) 场站短路比RSCRS1 5 0.000370+j0.093000 0.002141+j0.105 2.134
下载: 导出CSV
表 3 新能源场站并网点C2(330kV)的RSCRS2
Table 3 RSCRS2 of the grid connection point C2
算例 ˙ZT4(折算值) ˙ZT3, 1(折算值) ˙ZT3, 3(折算值) 场站短路比RSCRS2 6 j0.0495 0.0003-j0.0043 0.0002+j0.0332 1.725 7 0.000370+ j0.093000 0.000256+ j0.031333 0.000904+ j0.038556 1.985
下载: 导出CSV
表 4 不同调相机配置下新能源场站并网点MRSCRS
Table 4 MRSCRS of the grid connection point with different synchronous condenser configurations
新能源场站并网点 初始方式无调相机 加装调相机 并网点1 2.41 3.28 并网点2 2.37 3.23 并网点3 2.08 2.86 并网点4 2.05 2.84 并网点5 1.96 2.58 并网点6 1.84 2.40 并网点7 1.97 2.69 并网点8 1.92 2.62 并网点9 2.08 2.92 并网点10 1.83 2.51 并网点11 1.99 2.78 并网点12 2.12 3.02
下载: 导出CSV
表 5 初始无调相机方式下新能源机端MRSCRG
Table 5 MRSCRG of the invertor terminal without synchronous condenser
新能源汇集站 新能源发电设备 机端母线MRSCRG 汇集站A 新能源1 1.61 新能源2 1.28 汇集站B 新能源3 1.34 新能源4 1.12 汇集站C 新能源5 1.82 新能源6 1.20
下载: 导出CSV
-
[1] 周孝信, 鲁宗相, 刘应梅, 等.中国未来电网的发展模式和关键技术[J].中国电机工程学报, 2014, 34(29):4999-5008. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201429002.htm ZHOU Xiaoxin, LU Zongxiang, LIU Yingmei, et al.Development models and key technologies of future grid in China[J]. Proceedings of the CSEE, 2014, 34(29):4999-5008(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201429002.htm
[2] 孙华东, 许涛, 郭强, 等.英国"8·9"大停电事故分析及对中国电网的启示[J].中国电机工程学报, 2019, 39(21):6183-6192. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201921002.htm SUN Huadong, XU Tao, GUO Qiang, et al.Analysis on blackout in Great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21):6183-6192(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201921002.htm
[3] 马进, 赵大伟, 钱敏慧, 等.大规模新能源接入弱同步支撑直流送端电网的运行控制技术综述[J].电网技术, 2017, 41(10):3112-3120. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201710003.htm MA Jin, ZHAO Dawei, QIAN Minhui, et al.Reviews of control technologies of large-scale renewable energy connected to weakly-synchronized sending-end DC power grid[J]. Power System Technology, 2017, 41(10):3112-3120(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201710003.htm
[4] 康重庆, 姚良忠.高比例可再生能源电力系统的关键科学问题与理论研究框架[J].电力系统自动化, 2017, 41(9):2-11. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201709002.htm KANG Chongqing, YAO Liangzhong.Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9):2-11(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201709002.htm
[5] 孙华东, 张振宇, 林伟芳, 等.2011年西北电网风机脱网事故分析及启示[J].电网技术, 2012, 36(10):76-80. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201210016.htm SUN Huadong, ZHANG Zhenyu, LIN Weifang, et al. Analysis on serious wind turbine generators tripping accident in northwest China power grid in 2011 and its lessons[J]. Power System Technology, 2012, 36(10):76-80(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201210016.htm
[6] 孙华东, 王宝财, 李文锋, 等.高比例电力电子电力系统频率响应的惯量体系研究[J].中国电机工程学报, 2020, 40(16):5179-5192. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC202016011.htm SUN Huadong, WANG Baocai, LI Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16):5179-5192(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC202016011.htm
[7] GB38755-2019电力系统安全稳定导则[S].北京: 国家标准化管理委员会, 2019. GB 38755-2019, Code on Security and Stability for Power System[S]. Beijing: Standardization Administration of the People's Republic of China, 2020(in Chinese).
[8] 全国电网运行与控制标准化技术委员会.《电力系统安全稳定导则》《电力系统技术导则》条文释义与学习辅导[M].北京: 中国电力出版社, 2020. Grid Operation and Control Standardization Technical Committee.Interpretation and guidance of code on security and stability for power system and guide in technology for power system[M]. Beijing: China Electric Power Press, 2020(in Chinese).
[9] TAYLOR C. W., Power system voltage stability[M]. New York: McGraw-Hill, 1994.
[10] IEEE Standards Board.IEEE Std 1204-1997 IEEE guide for planning DC links terminating at AC locations having low short-circuit capacities[S]. New York: IEEE, 1997.
[11] CIGRE.CIGRE Working Group B4.41.Systems with multiple DC infeed[S]. Paris: CIGRE, 2008.
[12] 辛焕海, 章枫, 于洋, 等.多馈入直流系统广义短路比:定义与理论分析[J].中国电机工程学报, 2016, 36(3):633-647. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201603006.htm XIN Huanhai, ZHANG Feng, YU Yang, et al.Generalized short circuit ratio for multi-infeed DC systems:definition and theoretical analysis[J]. Proceedings of the CSEE, 2016, 36(3):633-647(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201603006.htm
[13] ZHANG Y., HUANG S.H., SCHMALL J., et al.Evaluating system strength for large-scale wind plant integration[C]. IEEE PES General Meeting, National Harbor, USA, 2014.
[14] Report to NERC ERSTF for Composite Short Circuit Ratio(CSCR) Estimation Guideline[R]. Schenectady, NY, USA: GE Energy Consulting, 2015.
[15] CIGRE.CIGRE Working Group B4.41.Connection of Wind Farms to Weak AC Networks[S]. Paris: CIGRE, 2016.
[16] WU Di, LI Gangan, Milad Javadi, et al.Assessing impact of renewable energy integration on system strength using site-dependent short circuit ratio[J]. IEEE Transactions on Sustainable Energy, 2018, 9(3):1072-1080. DOI: 10.1109/TSTE.2017.2764871
[17] GB/Z 19963-2011风电场接入电力系统技术规定第一部分: 陆上风电[S].北京: 国家标准化管理委员会, 2011. GB/Z 19963-2011 Technical Specification for Connecting Wind Farm to Power System Part1: On-shore Wind Power[S]. Beijing: Standardization Administration of the People's Republic of China, 2011(in Chinese).
[18] System Strength Impact Assessment Guidelines[R]. Australia: Operator, Australian Energy Market, 2018.
[19] 林伟芳, 汤涌, 卜广全.多馈入交直流系统短路比的定义和应用[J].中国电机工程学报, 2008, 28(31):1-8. DOI: 10.3321/j.issn:0258-8013.2008.31.001 LIN Weifang, TANG Yong, BU Guangquan.Definition and application of short circuit ratio for multi-infeed AC/DC power systems[J]. Proceedings of the CSEE, 2008, 28(31):1-8(in Chinese). DOI: 10.3321/j.issn:0258-8013.2008.31.001
[20] Procedimientos De Verificación[EB/OL]. https://www. aeeolica.org/images/Grupos_trabajo/Comite_tecnico_verificacion/PVVC_11.pdf, 2018-9-26.
[21] Australian Energy Market Operator.Recommended Technical Standards For Generator Licensing in South Australia[EB/OL]. http://www.escosa.sa.gov.au/Article Documents/1048/20170331-Inquiry-RecommendedTechnicalStandardsGeneratorLicensingSA-AEMOadvice.pdf.aspx?Embed=Y, 2017-3-31.
[22] 华为.光伏电站弱电网支撑技术白皮书[EB/OL]. https:// solar.huawei.com/zh/download?p=%2F-%2Fmedia%2FSolar%2Fminisite%2FSnec%2Fresources%2FGrid-friendly-whitebook.pdf,2020-8.
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
下载:
