0.   引言

电力电子技术广泛应用于日常生活与工业应用中，在给人类带来便利的同时也给电网谐波治理造成了一定的困难，国际电工委员会(IEC)和美国电气和电子工程师协会(IEEE)都对电力电子装置接入电网制定了相应的谐波抑制标准，例如当功率大于75W的电源产品接入电网时要满足相应的功率因数等要求^[1-3]。随着科技和工业发展的需要，电力电子技术的应用越来越广泛，使得功率因数校正技术(power factor correction，PFC)在现代高品质整流系统中变得尤为重要。

在单相交流供电系统中通常采用两级式架构来实现电能变换，前级由PFC电路构成，将交流输入电压变换成直流母线电压，后级由DC-DC变换器构成，给负载提供所需的、稳定的直流电压^[4-6]。为了提升电源系统的转换效率，许多学者在这两方面进行了大量的研究工作，其中在前级PFC电路中，通常采用减少电流流通路径上半导体器件数目来减小导通损耗，以达到提升效率的目的^[7-10]。因此，在过去的数十年里，Boost型无桥PFC变换器受到了学者的广泛关注^[11-12]。其中基本无桥PFC变换器因器件少、结构简单、易驱动等特点一度成为研究热点，但由于输入电压浮地会产生较大的共模噪声，导致电磁干扰问题严重^[13-14]。针对此问题，带有钳位二极管的双Boost无桥PFC变换器被提出，可以有效地克服共模噪声，但较多的元器件数量以及较高成本限制了其进一步的应用。

图腾柱无桥PFC(totem-pole bridgeless PFC，TPBL PFC)变换器由于输入端在每半个工频周期由二极管钳位至输出，较其他无桥拓扑拥有较低的共模噪声；同时较少的元器件数目和较高的器件利用率使其极具工程应用价值。然而，由于大多数硅基MOSFET其寄生体二极管较差的反向恢复特性，使得TPBL PFC变换器只能工作在断续导电模式(discontinue conduction mode，DCM)或者临界导电模式(boundary conduction mode，BCM)^[15-16]，近些年来，随着新型器件的发展，基于氮化镓MOSFET所构成的图腾柱式无桥PFC，由于没有反向恢复时间问题使得其可工作在连续导电模式(continuous conduction mode，CCM)而备受学术界及工程师们关注。但是目前氮化镓MOSFET构成的变换器多用于小功率场合，大功率氮化镓器件不仅产品种类少、价格昂贵，而且还存在性能退化以及可靠性较低等问题，限制其进一步应用^[17-22]。

基于上述问题，为了使得基于硅基MOSFET的图腾柱无桥PFC变换器能可靠地工作在CCM模态下，许多学者也在拓扑优化方面做了大量工作。例如文献[23]提出一种利用零电压转换(zero-voltage transition，ZVT)技术，通过增加谐振电感和辅助开关组成有源谐振支路实现主开关管的ZVS和二极管的ZCS，但由于谐振电感两端电压受到输入和输出电压的限制，很难在全范围内实现ZVS，此外辅助电路损耗较大；文献[24]通过增加一个无源LC谐振网络来实现图腾柱无桥变换器的软开关，使其可工作在CCM模式下，由于无源谐振支路在整个开关周期中均工作，且串联在功率回路中，使得导通损耗较大，变换器效率提升不明显；文献[25]提出一种并联交错的软开关拓扑，通过辅助电感和移相控制来实现全输入电压范围和负载范围的ZVS，然而辅助电感的峰值电流较大，并且在开关周期中存在时间较长，轻载时导通损耗较大；文献[26]在文献[25]基础上，利用耦合电感的漏感降低开关损耗，但在轻载条件下很难实现ZVS。

在上述设计思路的启发下，本文提出一种可工作于CCM的图腾柱无桥PFC变换器解决方案。该方案在传统图腾柱无桥PFC拓扑基础上仅需增加少量器件，通过利用电感与开关管输出电容的谐振实现主开关管ZVS开通；电感的谐振电流限制了体二极管的di/dt，减缓体二极管的反向恢复问题并实现ZCS关断；克服传统图腾柱无桥PFC电路只能工作在DCM或BCM的限制，提高变换效率与功率密度。下面将首先对该变换器的电路拓扑和其工作原理展开介绍，然后对其性能进行详细地分析，最后设计实验样机进行实验验证，并对实验结果进行分析得出相应结论。

1.   电路拓扑与工作原理

1.1   拓扑结构分析

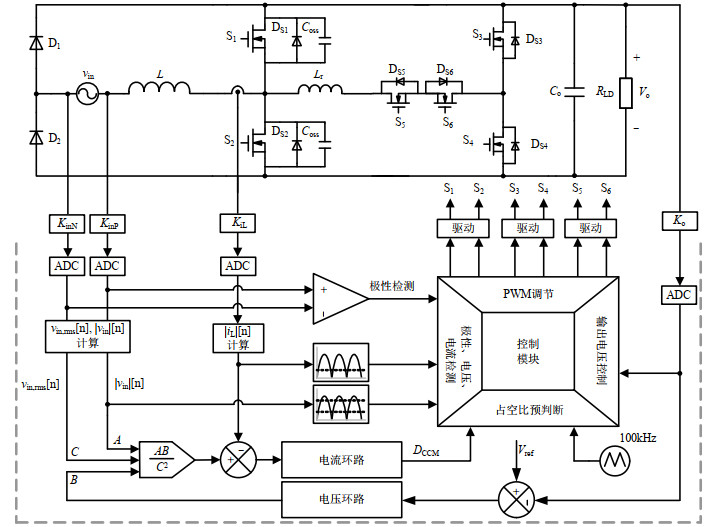
本文提出的可工作于CCM的图腾柱无桥PFC变换器是由传统的TPBL PFC变换器和有源辅助谐振腔组成。其中传统TPBL PFC变换器是主功率拓扑，在工频正半周期由升压电感L，主开关管S₂，体二极管D_S1以及二极管D₂构成；在工频负半周期由升压电感L，主开关管S₁，体二极管D_S2以及二极管D₁构成，其中D₁和D₂工作在工频。谐振电感L_r，辅助开关管S₃、S₄、S₅和S₆与主开关管的输出电容C_oss构成有源辅助谐振腔。C_o为输出滤波电容，R_LD为等效负载电阻。该变换器的本质是传统TPBL PFC变换器和有源谐振腔在输入电压正负半周期分别工作。其变换器拓扑图如图 1所示。

图  1  可工作于CCM模态图腾柱无桥PFC

Figure  1.  Totem-pole bridgeless PFC for CCM mode

下载: 全尺寸图片 幻灯片

1.2   工作模态分析

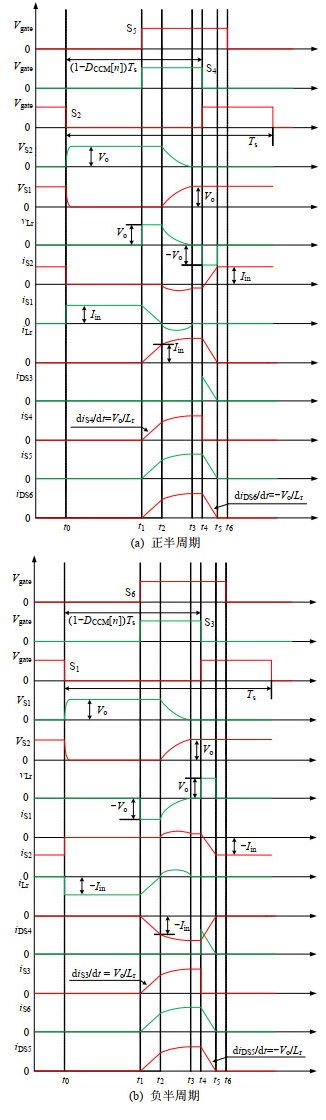
为简化分析，将开关管与二极管视为理想器件，忽略器件本身的开通时间、导通压降等问题。由于L足够大在一个开关周期内可以视为一个恒流源I_in，同理C_o可视为一个恒压源V_o。由于主开关管S₁和S₂在输入电压v_in的正、负半周期交替工作，工作过程完全对称，因此本文仅对输入正半周的1个开关周期做模态分析。变换器关键波形如图 2所示，具体工作模态分析如图 3所示。

图  2  一个开关周期内的关键波形

Figure  2.  Key waveform in one switching cycle

下载: 全尺寸图片 幻灯片

图  3  变换器模态分析

Figure  3.  Operating modes of the proposed converter

下载: 全尺寸图片 幻灯片

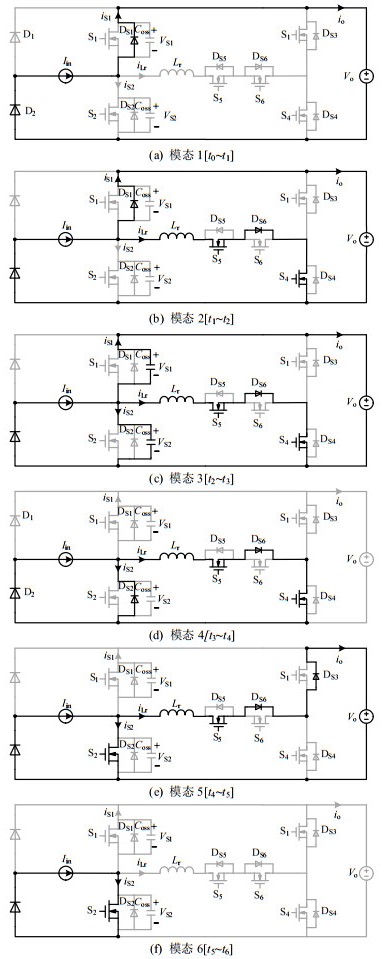
1）开关模态1([t₀, t₁])：如图 3(a)所示。在t₀时刻，S₂关断。在此时段内，由于S₂关断，储存在L中的能量通过D_S1释放到输出侧，此过程与传统TPBL PFC变换器的续流过程完全相同。其中，由于S₄、S₅关断，有源辅助谐振腔未参与工作，谐振电感两端电压为零，谐振电感电流i_Lr(t)在此时段内无变化，保持为零。

2）开关模态2([t₁，t₂])：如图 3(b)所示。在t₁时刻，S₄、S₅导通。在此时段内，忽略电流流通路径上的电阻和二极管管压降，谐振电感两端承受的电压为输出电压V_o，i_Lr(t)线性增加。有方程：

约束条件为：i_Lr(t₁)=0，i_Lr(t₂)=I_in。

由于谐振电流是从零开始增加的，且电流的变化速率受到谐振电感L_r的限制，因此S₄、S₅实现零电流开通，D_S6自然开通。在t₂时刻，谐振电流线性增加到与升压电感电流I_in相等，D_S1电流线性下降为零，可控的di/dt消除了反向恢复的影响，因此实现了D_S1的零电流关断。此时段的持续时间T₁为

3）开关模态3([t₂, t₃])：如图 3(c)所示。由于在t₂时刻D_S1电流降为零，而S₂尚未开通，v_S1仍为零，D_S1反向恢复损耗接近为零。在此时段内，S₁和S₂的输出电容C_oss开始充电放电，并与谐振电感发生串联谐振，谐振频率为

在此开关模态下，谐振电感的端电压逐渐减小，电流持续上升，到t₃时刻，其两端电压降为零，谐振电流i_Lr(t)达到此开关周期内的最大值，此时谐振结束。有方程：

约束条件为：V_S2(t₂)=V_o；V_S2(t₃)=0。

其中，在t₃时刻谐振电流达到最大值：

谐振时间Τ₂如式(6)所示：

4）开关模态4([t₃, t₄])：如图 3(d)所示。在t₃时刻谐振结束，此时D_S2导通，谐振电感电流续流，忽略电流流通路径上的电阻和二极管管压降，谐振电感两端电压为零，谐振电感电流i_Lr(t)在此时段内无变化，保持为最大值，S₂达到了零电压开通条件。在此时间段内触发栅极导通S₂即实现了ZVS。另外，S₄、S₅与S₂之间的栅极触发信号有一定的时间差T_d，如式(7)所示：

5）开关模态5([t₄, t₅])：如图 3(e)所示。在t₄时刻S₄关断，存储在谐振电感中的能量通过S₅的沟道，S₆和S₃的体二极管泄放到输出侧，忽略电流流通路径上的电阻和二极管管压降，谐振电感两端承受反向的输出电压−V_o，谐振电流线性下降，因此有方程：

约束条件为：i_Lr(t₄)=i_Lr(t₃)，i_Lr(t₅)=0。谐振电流降到零所需要的时间T₃如式(9)所示：

理想情况下，谐振电感电流i_Lr下降到零后不再发生变化，一直持续到下一个开关周期，S₃、S₆的体二极管自然关断。但是由于受到体二极管结电容和反向恢复的影响，体二极管D_S3和D_S6仍具有导电性，谐振电流在经过反向之后截止。

6）开关模态6([t₅, t₆])：如图 3(f)所示。在t₅时刻谐振电流降为零，延迟少许时间后在t₆时刻关闭S₅的驱动信号，此时S₅实现ZCS。

至此，变换器将进入到下一个开关周期过程中，一个开关周期内的所有开关模态分析完毕。

2.   电路讨论与控制

2.1   软开关约束条件

从变换器的模态分析可知，通过主开关管S₁、S₂与辅助开关管S₃~S₆的交错导通，可实现S₁、S₂的ZVS和其体二极管D_S1、D_S2的ZCS。仅以正半周期为例，在D_S1续流时，谐振电感限制了其电流下降率，S₂导通之前其电流下降为零，实现了S₁的ZCS；而在S₂开通时，须要将其输出电容C_oss上储存的电荷全部释放，即v_S2=0，才能实现ZVS。

在体二极管D_S1续流阶段，首先预导通辅助开关管S₄、S₅，当谐振电流i_Lr上升至与升压电感电流I_in相等时，谐振电感开始与S₁、S₂的输出电容C_oss发生串联谐振，在将C_oss上的电荷释放到零后，开通S₂即实现了ZVS。为可靠实现软开关，需保证D_S1的续流时间至少大于T_d，由此得出可工作于CCM的图腾柱PFC变换器实现软开关的其中一个约束条件：

式中：D_CCM是变换器工作在CCM模式下的占空比；T_s是变换器的一个开关周期。

在S₂实现了ZVS后，谐振电感电流需要泄放至输出侧，因此，S₂的导通时间要比谐振电感电流的泄放时间长，以保证谐振电感储存的能量全部释放完毕。由此得出该变换器实现软开关的另一个约束条件：

只有满足上述2个约束条件，才能实现输出电容C_oss能量的转移与释放，实现开关管的ZCS和ZVS。另外，有源辅助谐振之路只在主开关管开通的瞬间工作，不会增加主电路功率器件的电压、电流应力，并且产生的额外损耗也非常小。当不满足上述2个约束条件时，有源辅助谐振之路停止工作，变换器按照传统图腾柱无桥PFC的工作方式运行。因此，软开关的约束条件不会对变换器产生其他影响。

2.2   控制策略

所提出的变换器工作在CCM模式，采用平均电流控制方式来减小由跟踪误差产生的电流畸变，控制框图如图 4所示。与传统的有桥PFC变换器有所不同，可工作于CCM的图腾柱无桥PFC变换器增加了输入电压极性检测环节，用来检测输入电压的正负半周期。

图  4  变换器控制框图

Figure  4.  Converter control block diagram

下载: 全尺寸图片 幻灯片

在本文中，采用TI公司的高性能微控制器进行整个系统的环路及时序控制，具体型号为TMS320F28335；采用TI公司的高速驱动器驱动开关管，具体型号分别为UCC27712、UCC27710和UCC27424；采用LEM公司的霍尔电流传感器进行电流采样，具体型号为CASR 6-NP。控制器包含内外2个控制环路，其中外环是输出电压控制环路，用来控制调节变换器的平均输出电压；另一个内环是输入电流控制环路，用来调节输入电流的相位，以使得输入电流跟随输入电压，两者相位差为零，来达到功率因数校正的目的。

为简化控制，主开关管S₁、S₂使用相同的驱动信号，辅助开关管S₃、S₄使用相同的驱动信号，S₅、S₆使用相同的驱动信号。v_c为三角载波，利用三角载波与占空比D_CCM作比较分别产生主开关管S₁、S₂的驱动以及辅助开关管S₃、S₄、S₅和S₆的驱动。开关管的时序图如图 5所示，现仅以正半周为例，其控制策略如下：当1 > v_{c_up} > D_CCM和1 > v_{c_down} > D_CCM+T_d/T_s时，开关管S₁、S₂、S₃、S₄、S₅和S₆均保持关断，变换器工作在开关模态1；当D_CCM +T_d/T_s > v_{c_down} > D_CCM时，辅助开关管S₄、S₅开通，变换器进入开关模态2，谐振电流线性增加，当谐振电流i_Lr(t)=I_in时，模态2结束，变换器进入开关模态3。此时谐振电感和开关管输出电容C_oss开始串联谐振，谐振结束后变换器进入开关模态4，主开关管S₂达到ZVS开通的条件，此时段的持续时间为T_d；当D_CCM > v_{c_down} > D_CCM–T₃/T_s时，变换器进入开关模态5，辅助开关管S₄关断，谐振电流释放至输出侧，主开关管S₂开通实现ZVS。谐振电流释放到零，辅助开关管S₅关断，开关模态6结束，此时段的持续时间为T₃。

图  5  正(负)半周辅助开关管时序图

Figure  5.  Implementation of auxiliary switch in positive(negative) half cycle

下载: 全尺寸图片 幻灯片

由上述分析可知，首先需要对输入电压进行极性检测和采样，判断正负周期和过零点，再通过数字电压环路和电流环路产生所需要的占空比D_CCM，根据极性的判断驱动相应的主功率开关管；辅助开关的驱动则需要先对占空比的大小进行判断，进入相应的软开关范围后，提前开通T_d时间完成串联谐振，在S₂实现零电压开通后，延迟T₃时间关闭辅助开关即可。此外，对输出电压V_o进行监测，当输出电压超过设定值时，将停止PWM输出，实现对电路保护。

3.   参数设计及软开关范围

3.1   变换器参数设计

TPBL PFC变换器升压电感L的电流纹波量取最大基波峰值电流的20%，当变换器工作在最低输入电压情况下，峰值时的占空比D_PLL为

式中V_{in_min}为输入电压的最小有效值。

则最大的基波峰值电流I_{in_pk}为

则功率电感的纹波电流ΔI_L为

式中：P_o为变换器的额定功率；η为满载时的效率。

则功率电感L的电感量为

式中f_s为变换器的开关频率。

如果功率电感的纹波电流很大，变换器的开关损耗将会减小，然而，较大的纹波电流会有大的电流有效值，因此磁芯损耗和导通损耗又会增加。在本文所提出的变换器中，开关损耗以通过增加谐振电路来减小，因此功率电感可以设计成具有较小的纹波电流，以减小变换器的磁芯损耗和导通损耗。

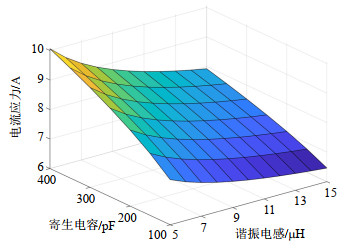
由式(5)可得开关管寄生电容C_oss、谐振电感L_r和谐振电流应力的关系曲线，如图 6所示。可以看出：1）当L_r一定时，随着C_oss的增大，谐振电感电流应力逐渐增大；2）当C_oss一定时，随着L_r的增大，谐振电感电流应力逐渐减小。此外谐振电感必须足够大来减小开关和体二极管的di/dt，但是过大的电感量会导致磁芯损耗和导通损耗的增加，所以谐振电感要根据以上情况进行折中考虑。

图  6  电流应力关系图

Figure  6.  Current stress diagram

下载: 全尺寸图片 幻灯片

本文提出的变换器选取谐振时间为3倍的反向恢复时间t_rr，因此谐振电感量L_r可通过式(16)计算得到：

由工作模态分析可知，主功率开关管S₁、S₂的峰值电流I_peak为

开关管S₁、S₂的有效值电流I_rms为

续流体二极管的平均电流I_D为

TPBL PFC变换器设定参数如下：额定输入电压为150~220V，输出电压为380V，额定输出功率为1kW，开关频率为100kHz。主电路各功率器件的设计主要考虑理论上的最低输入电压(V_{in_min}=150V)，满负载输出时的情况，设定在最小电压输入时，整机效率为η=0.9。

通过上述公式可求得，变换器在宽电压输入宽负载输出范围内电感电流基波峰值为I_{in_pk}=10.4A，最大纹波电流为ΔI_L=2A，此时包含谐波电流的最大电感电流峰值为I_{in_max_pk}=12.4A。在宽电压输入宽负载输出范围内，所有开关管S₁~S₆和二极管D₁、D₂的最大电压均为V_o=380V，主开关管S₁、S₂的电流峰值为I_peak=12.4A，有效值电流为I_rms=3.6A，续流体二极管的平均电流为I_D=1.3A，流过辅助开关管S₃~S₆的电流峰值I_{aux_pk}为

在最低输入电压时，主开关管S₁、S₂的最小占空比为D_PLL=0.44，升压电感L的最小感值为：L=0.47mH，保留一定的工程设计裕量，本文选取0.5mH。谐振电感L_r选取10μH，输出电容C_o选择800~1000μF，450V的电解电容。

3.2   软开关实现范围

由于工作在CCM模式下，TPBL PFC变换器变化的占空比与其输入电压、输出电压有关，变化的占空比如式(21)所示：

通过变换器模态分析可知，软开关的实现条件又受到了占空比的约束，因此根据约束条件式(10)、(11)及(21)可得到变换器占空比的工作上限为

占空比的工作下限为

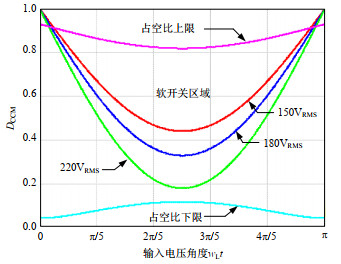
从式(22)和(23)可以看出，占空比的工作上限、下限决定了变换器软开关范围的宽度，在输入电压最低且满载的时候，占空比工作上限最低、工作下限最高、软开关范围最窄，变换器所处的工作状态也最为恶劣。因此在该条件下求得的占空比上限、下限也满足其他条件下变换器软开关实现对占空比的要求。图 7为不同输入电压条件下变换器软开关范围，可以看出，软开关区域基本覆盖整个占空比区域，实现全输入范围的软开关功能。曲线条件：P_o=1kW，V_o=380V，T_s=10μs，L_r=10μH，η=0.9，C_oss=200pF。

图  7  变换器软开关实现范围

Figure  7.  Scope of converter soft switching

下载: 全尺寸图片 幻灯片

当输入电压V_in在过零点附近时，变换器的占空比非常大接近于1，超过了占空比上限，升压电感电流通过体二极管续流时间非常的短，谐振电路没有足够的时间去完成串联谐振，不能满足式(10)。但由于在过零点附近时，输入电流也非常小，变换器工作在DCM模态，体二极管实现自然零关断；在输入电压V_in的峰值时，如果峰值过高，则变换器的占空比非常小，接近于0，低于占空比下限，谐振电路在串联谐振过后没有充足的时间去泄放谐振电流，不能满足式(11)，导致电路会有较大的环流影响变换器效率。分析可知，该变换器能够在较宽的输入电压范围和负载输出范围内，达到各开关器件软开关的设计要求。

4.   实验验证

为验证所提出变换器设计方案的可行性、理论分析的正确性和控制策略的有效性，搭建1台实验原理样机，该样机额定功率1kW，如图 8所示，其主要电路参数如表 1所示。

图  8  原理样机图片

Figure  8.  A photo of experimental prototype

下载: 全尺寸图片 幻灯片

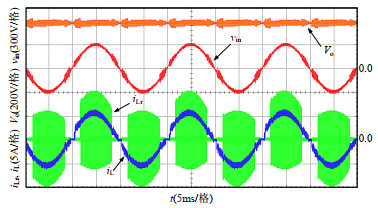
表  1  TPBL PFC变换器电路参数

Table  1.  Circuit parameters of the proposed converter

变量(符号)	参数
输入电压有效值vin/V	150~220
输出电压Vo/V	380
输出功率Po/W	1000
电网频率f/Hz	50
开关频率fs/kHz	100
主开关管S1、S2	SIHB33N60E-GE3
辅助开关管S3~S6	FDD8N50NZ
二极管D1、D2	APT40DQ60BG
升压电感L/μH	500
谐振电感Lr/μH	10
开关管输出电容Coss/pF	200
输出滤波电容Co/μF	1000

下载: 导出CSV 

| 显示表格

图 9为额定负载时输入电压v_in、输出电压V_o、升压电感电流i_L与谐振电感电流i_Lr的实验波形。由图 9可见，输入电压v_in有效值约为220V，i_L很好地跟随了输入电压v_in的波形，且两者相位相同，因此达到功率因数校正目的，同时得到稳定的直流输出电压。

图  9  额定电压和满载时v_in、V_o、i_L、i_Lr波形

Figure  9.  Waveforms of the voltage v_in, V_o and the current i_L, i_Lr at rated voltage and full load

下载: 全尺寸图片 幻灯片

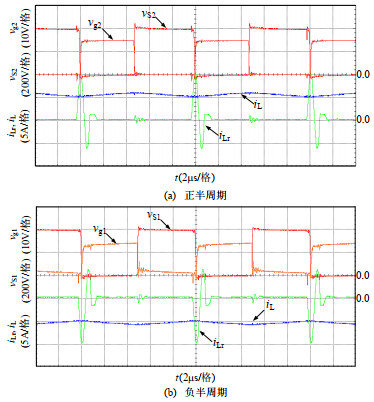
图 10为变换器在交流正、负半周期内若干个开关周期内主开关S₁、S₂漏源极电压v_S1、v_S2和其栅极驱动电压v_g1、v_g2、升压电感电流i_L与谐振电感电流i_Lr的实验波形。由图 10可见，本文所提出的变换器没有电压、电流尖峰，减小了开关器件应力。此外，谐振电感电流i_Lr仅仅出现在主开关管导通前的较窄时间段，该谐振电流对输入电流的影响较小，不会产生较大附加损耗。

图  10  主开关管电压、驱动和i_L、i_Lr波形

Figure  10.  Waveforms of the voltages and gate voltages of the main switches and the current i_L, i_Lr

下载: 全尺寸图片 幻灯片

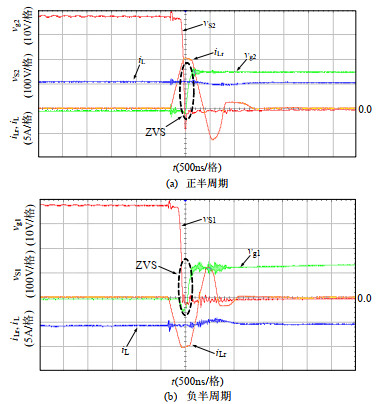
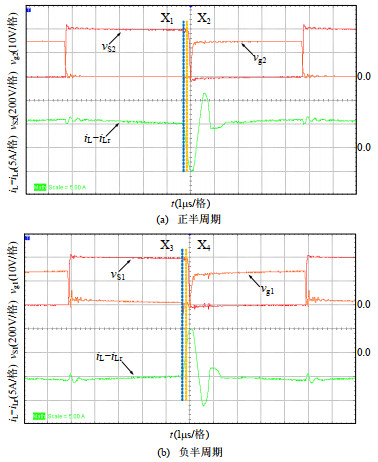
图 11为变换器在交流正、负半周期内主开关管S₁、S₂的ZVS实验波形，虚线部分为开关管两端电压v_S1、v_S2与驱动电压v_g1、v_g2的交叠区。其中图 11(a)为输入正半周期工况下主开关S₂工作波形，可以看出，在开通S₂之前，其两端电压v_S2先下降到零，随后体二极管D_S2导通，此时开通S₂即实现了ZVS；其中图 11(b)为输入正半周期工况下主开关S₁工作波形，可以看出，在开通S₁之前，其两端电压v_S1先下降到零，随后体二极管D_S1导通，此时开通S₁即实现了ZVS。

图  11  ZVS开通波形

Figure  11.  Waveforms of ZVS turn-on transition

下载: 全尺寸图片 幻灯片

图 12为变换器在交流正、负半周期内主开关管S₁、S₂的ZCS实验波形。其中图 12(a)为输入正半周期工况下主开关S₂工作波形，谐振电路在t_x1时刻开始工作，i_L~i_Lr为开关管S₁的电流，此电流线性下降，在t_x2时刻下降为零，而此时主开关管S₂并未导通。可控的电流消除了反向恢复的影响，实现了S₁的ZCS。图 12(b)为输入负半周期工况下实现S₂的ZCS波形，工作原理与图 12(a)相同。

图  12  ZCS关断波形

Figure  12.  Waveforms of ZCS turn-off transition

下载: 全尺寸图片 幻灯片

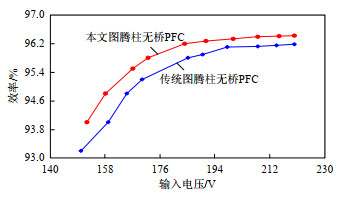
图 13为所提出的变换器原理样机与传统TPBL PFC变换器的效率对比曲线。通过输入电压在150~220V之间变化，输出功率1kW的实验条件对比下，本文所提出的变换器取得了较理想的效率曲线，并且在输入电压为220V时达到效率峰值96.3%。而且相较于传统的TPBL PFC变换器，效率提升达1.7~2%，显示了该变换器有效降低了各开关管的开关损耗。

图  13  满载时效率随输入电压的变化曲线

Figure  13.  Measured power efficiencies with relation to the line at full load

下载: 全尺寸图片 幻灯片

5.   结论

本文提出一种可工作于CCM模态的高效图腾柱无桥PFC变换器，该变换器实现主开关管的ZVS开通和ZCS关断，解决其寄生体二极管反向恢复的问题，拓展硅基MOSFET的图腾柱无桥PFC的工作范围，提高变换器效率与功率密度。通过对该变换器工作模态的详细分析，得出变换器工作在软开关状态下的约束条件与范围，在此基础上，提出变换器的控制策略，进行有源辅助谐振之路的相关参数设计。最后设计1台额定输出380V/1000W的试验原理样机，实验结果证实了该设计方案的可行性和理论分析的正确性，通过对比分析，该变换器相较于传统TPBL PFC变换器效率能进一步提升。