Distributed Load Security Domain and Its Application (I): Line Load Security Domain for Grid Static Security
-
摘要: 维持多电压等级(简称多级)电网全局电压安全与静态功-角稳定的分散线路功率约束问题，分析困难、现有理论依据不足。研究发现，多级电网的电压幅值呈“锯齿分布”特征，维持全网电压安全水平的关键是限制各线路的压差；前期研究得到的线路负荷安全域，对线路压差约束起主导作用。进一步研究发现，线路的允许压差、负荷安全域大小和域内最大功角，三者对应且近似呈正比关系；无论何种拓扑形式，各级电网中的有功路径最大功角取决于该级电网内的允许压差；但维持允许压差的线路负荷安全域约束，可能导致多级电网有功路径的功角超限，不满足静态功-角稳定的充要条件。故提出了线路负荷安全域的修正方法：如考虑负荷功率因数、采用串联阻抗或分配线路限制压差等方法缩小安全域。验算表明，修正后的线路负荷安全域，在约束安全压差的同时，还可满足多级电网的静态功-角稳定要求。该局部功率约束条件，可广泛应用于全网优化控制、分散安全控制和网架、无功规划等，具有理论和实际价值。Abstract: The problem of distributed power constraint of lines to maintain the global voltage security and static power-angle stability of multiple voltage level (multi-level for short) power grid is difficult to analyze and lacks sufficient theoretical basis. The analysis found that the voltage amplitude of multi-level grid has a "sawtooth distribution" characteristic, and the key to maintaining the global grid voltage safety level is to limit the voltage differential of each line. The line load security domain obtained in the previous study plays a leading role in restraining the voltage difference of lines. Further research found that the allowable pressure difference of the line, the size of load safety domain, and the maximum power angle in the domain correspond to each other and approximately proportional. Regardless of the topology, in each level of power grid, the maximum power angle of the active path depends on the allowable voltage difference; but due to the lines load security domain constraint of maintaining the allowable voltage difference, the power angle of the active power path in the multi-level grid may exceed the limit, which does not meet the necessary and sufficient condition for static power-angle stability. Therefore, the correction methods for the safety zone of the line load were proposed. For example, considering the load power factor, using series impedance or distributing the line can limit the voltage difference to reduce the safety zone. Checking calculations show that the revised line load security domain can meet the static power-angle stability requirements of multi-level power grids while constraining the safety pressure difference. This local power constraint can be widely used in global optimization control, decentralized safety control, grid and reactive power planning, etc. It has great theoretical and practical significance.
-
0. 引言
当前，无论从理论还是实际运行与规划的角度，维持多电压等级(简称多级)电网全局电压安全水平与静态功–角稳定的分散线路功率约束问题，都亟需深入研究以取得实质进展和突破。
由于节点、支路状态量之间的非线性耦合关系复杂，为便于理论分析和解决实际工程问题，将电网静态稳定性分解为电压稳定性、功–角稳定性，即功率–电压幅值关系、有功–相位角差关系的稳定性。但随后发现，进入强非线性后2种稳定边界难以区分[1-4]，满足2种稳定的共同约束条件，也难以确定[5]。
由于正常运行允许的电压水平远高于静态电压稳定极限，故研究维持全网电压安全水平的方法更具实际意义。由于节点电压之间的相互关联，全网电压安全控制也非易事。目前，国内外推广使用的自动电压控制(automatic voltage control，AVC)系统[6-9]，一般基于多级电网的无功优化，对分散的励磁系统、无功补偿、可调变比进行广域协调控制，以保持多点电压安全并降低网损[10-11]。但由于众多被控对象的性能和约束各异[12]、对电网模型精度和边界条件的依赖、以及电网分级管控机制等多种原因，反倒凸显出全局与分散电压安全控制理论相结合的重要性。另外，无论是电压/无功全局优化所给定的线路有功约束，还是分散电压安全控制的功率约束，也都与静态功–角稳定性相关。
“功–角稳定性”一般指交流电力系统的“同步能力”。由于发电机是系统主要元件，且初期的不稳定现象主要是远方机组的转速、功率不稳，故最初的静态功–角稳定性研究，主要基于单机–无穷大模型，分析发电机在同步约束下的有功输出特性及能力。后来，将有功传输的“同步能力”分析移植到线路，提出了线路的静态“极限功角”、“极限传输功率”等概念[13-15]，并参照发电机考虑静储备系数[16]，在工程上沿用至今。但实际运行中，往往联络线功率远未达到理论极限功率，便开始波动，甚至振荡。故工程上常取90°功角对应的极限功率的1/5~1/3作为实际线路有功限额。
20世纪50年代，国外在给定线路两端电压幅值后，发现两端的复功率点轨迹为对应圆弧[17]。故根据首、末端圆弧上对应功率及功角(线路的相位角差)的变化特征，研究线路的功率传输极限问题[17-18]。但线路的极限功率约束与电网静态功–角稳定性的关系一直未得到深入清晰的分析阐述。北美电力可靠性委员会(North American electric reliability council，NERC)在20世纪90年代提出研究电网可用输电能力[19]，但至今仍未见实质理论突破。
本课题组前期研究取得了一些有意义的进展。通过对戴维南等值模型的P-Q-U几何特性分析，得到了维持负荷侧电压安全水平的线路负荷安全域[20]，提出了基于负荷安全域匹配的维持多级电网电压安全水平的方法[21]。另外，在多级电网静态功–角稳定性研究方面，基于电网的映射弹性网模型[22-23]，分析得到了多级电网静态功–角稳定的充要条件[24-25]，即每条有功路径都满足静态功–角稳定。但是，文献[21]对全网电压解耦性仍分析不足，也未涉及电网静态功–角稳定性问题; 文献[25]未具体分析线路功率约束问题。
本文首先分析全网电压安全的分散性特征，研究线路负荷安全域的电压分散控制特性，然后研究其作为线路功率约束能否满足全网静态功–角稳定性，以及相应的修正方法。在此基础上，研究其作为全网分散安全控制和规划约束的可行性。
1. 基于线路压差约束的分散电压安全性
1.1 线路压差主导的全网电压安全水平
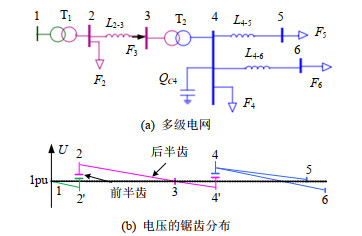
发电机升压并网后，输出的有功功率都是从高压电网逐级降压，经过4—6个等级，最终流向实际的低压负荷。功率流经线路一般都会产生电压幅值差(本文简称压差，因压降已被教材定义为电压相量差)，故多级电网的节点电压幅值的标幺值呈“锯齿分布”特征，如图 1所示。
![]()
图 1 多级电网节点电压的锯齿分布特征Figure 1. Sawtooth distribution feature of node voltage in multi-level power grid图 1中，将变压器内变比提升的电压标幺值部分称为“前半齿”，如2'-2、4'-4段; 将线路及变压器支路的压差部分称为“后半齿”，如2-3-4'段。当然，若长线轻载，线路末端电压偏高，后半齿也可能上扬。
由图 1可知，只要“后半齿”中的线路压差过大，无论如何调整“前半齿”(即变比)，2、3、4、5、6节点中，总有节点电压幅值越限。所以，维持多级电网中所有节点电压安全水平的关键及必要条件，是约束“后半齿”的线路压差。因为只要压差在允许范围内，配合微调变比(即前半齿)，即可保持全网节点电压水平良好，不发生上、下越限。
1.2 线路压差与功率的关系
线路及变压器压差主要取决于线路负荷功率，包括末端的无功补偿量。但是，线路压差与功率的关系复杂，须经复数运算。
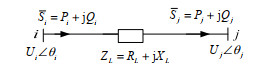
以图 2所示的简单线路模型为例。设线路L首、末端电压${\dot U_i}$、${\dot U_j}$的相位差为θij，阻抗为ZL=RL+jXL，阻抗角为α。图 2中，节点电压与线路功率的关系为
$${\dot U_i} = {U_j} + \frac{{{P_j}{R_L} + {Q_j}{X_L}}}{{{U_j}}} + {\rm{j}}\frac{{({P_j}{X_L} - {Q_j}{R_L})}}{{{U_j}}}$$ (1) 由式(1)可得首端电压幅值为
$${U_i} = \sqrt {{{({U_j} + \frac{{{P_j}{R_L} + {Q_j}{X_L}}}{{{U_j}}})}^2} + {{(\frac{{{P_j}{X_L} - {Q_j}{R_L}}}{{{U_j}}})}^2}} $$ (2) 由式(1)、(2)可见，线路的首、末端压差ΔUij=Ui-Uj与Uj、Pj、Qj复杂耦合。
所以，工程上简化为
$$\Delta {U_{ij}} \approx \frac{{{P_j}{R_L} + {Q_j}{X_L}}}{{{U_j}}} + \frac{{{{({P_j}{X_L} - {Q_j}{R_L})}^2}}}{{2U_j^3}}$$ (3) 式(3)仍旧较为复杂，故进一步分别简化为
$$\Delta {U_{ij}} = {U_i} - {U_j} \approx \frac{{{P_j}{R_L} + {Q_j}{X_L}}}{{{U_j}}}$$ (4) 若Uj≈1pu，则式(4)简化为
$$\Delta {U_{ij}} \approx {P_j}{R_L} + {Q_j}{X_L}$$ (5) 式(4)、(5)看似简洁完美地实现了基于线路负荷功率的压差表征，但工程精度值得商榷。由式(2)—(4)可见，压差还与节点电压耦合，单纯的代数分析，难以推导线路压差约束对应的功率范围。
下面通过代数–几何分析法，给出压差约束对应的线路复功率区域范围。
2. 安全压差约束主导的线路负荷安全域
2.1 简单线路模型的功率域
以图 2线路模型为例，该线路末端复功率为
$${\tilde S_j} = {P_j} + {\rm{j}}{Q_j} = {\dot U_j}{(\frac{{{{\dot U}_i} - {U_j}\cos {\theta _j} - {\rm{j}}{U_j}\sin {\theta _j}}}{{{\rm{|}}{Z_L}{\rm{|}}\cos \alpha + {\rm{j|}}{Z_L}{\rm{|}}\sin \alpha }})^ * }$$ (6) 式(6)展开后可分别得到有功、无功的表达式：
$${P_j} = \frac{{{U_i}{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}}\cos (\alpha - {\theta _{ij}}) - \frac{{U{{_j^{}}^2}}}{{{\rm{|}}{Z_L}{\rm{|}}}}\cos \alpha $$ (7) $${Q_j} = \frac{{{U_i}{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}}\sin (\alpha - {\theta _{ij}}) - \frac{{U{{_j^{}}^2}}}{{{\rm{|}}{Z_L}{\rm{|}}}}\sin \alpha $$ (8) 由式(7)、(8)得到末端的功率与电压的关系：
$${({P_j} + \frac{{U{{_j^{}}^2}\cos \alpha }}{{{\rm{|}}{Z_L}{\rm{|}}}})^2} + {({Q_j} + \frac{{U{{_j^{}}^2}\sin \alpha }}{{{\rm{|}}{Z_L}{\rm{|}}}})^2} = {(\frac{{{U_i}{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}})^2}$$ (9) 同理，由首端的有功、无功表达式，也可得到对应的首端功率与电压的关系：
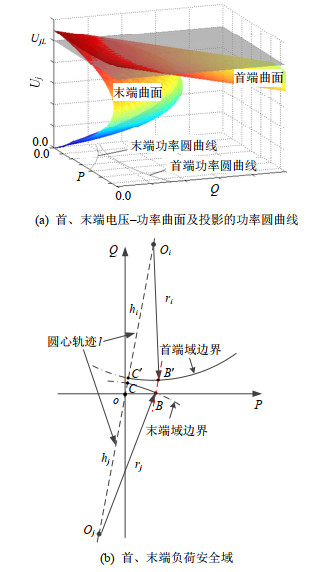
$${({P_i} - \frac{{U{{_i^{}}^2}\cos \alpha }}{{{\rm{|}}{Z_L}{\rm{|}}}})^2} + {({Q_i} - \frac{{U{{_i^{}}^2}\sin \alpha }}{{{\rm{|}}{Z_L}{\rm{|}}}})^2} = {(\frac{{{U_i}{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}})^2}$$ (10) 若Ui不变，式(9)、(10)分别为以末、首端功率为自变量的三维曲面函数Uj(Pj, Qj)、Uj(Pi, Qi)，如图 3(a)所示。
![]()
图 3 首、末端功率圆曲线及负荷安全域Figure 3. Power circular curve and load security domain at the head and end of the line当Uj=UjL时，将被切割的曲线投影到P-Q平面，分别得到首、末端功率圆曲线，如图 3(a)、3(b)所示。2个圆弧的圆心连线l经过原点，且斜率为tanα; 其平行线与2个圆弧的交点，即为首、末端的对应复功率顶点。由2个圆弧可得到第一象限的2个复功率区域：
1) 首端：${\tilde S_{iPQL}}(O{\rm{ - }}C'{\rm{ - }}B'{\rm{ - }}B{\rm{ - }}O) $;
2) 末端：$ {\tilde S_{jPQL}}(O{\rm{ - }}C{\rm{ - }}B{\rm{ - }}O)$。
若首、末端的复功率点分别落在${\tilde S_{iPQL}}$、${\tilde S_{jPQL}}$域内，则Uj > UjL。图 3(b)中，理论上末端复功率点可沿功率圆弧到达第四象限，即线路末端向线路输出无功。但此时首端对应的注入无功和线损都非线性大幅增加，故末端运行点一般不到第四象限。
2.2 线路功率域的压差约束主导特性
下面分析影响“线路功率域”大小的主导因子。
图 3(b)中，令圆心Oi、Oj到原点O的距离分别为hi、hj，半径为ri、rj。描述功率域${\tilde S_{iPQL}}$、${\tilde S_{jPQL}}$的大小，可用功率域边界上的最小视在功率Simin和Sjmin作为指标，即C′、C点到原点O的距离，如图 4所示。由式(9)、(10)可得：
$$\left\{ \begin{gathered} {S_{i\min }} = {h_i} - {r_i} = \frac{{{U_i} \cdot \Delta {U_{ij}}}}{{{\rm{|}}{Z_L}{\rm{|}}}} \\ {S_{j\min }} = {r_j} - {h_j} = \frac{{{U_j} \cdot \Delta {U_{ij}}}}{{{\rm{|}}{Z_L}{\rm{|}}}} \\ \end{gathered} \right.$$ (11) 实际运行时，Ui、Uj都非恒定，但一般都比ΔUij大一个数量级。故由式(11)可得灵敏度特性：
$$\left\{ \begin{gathered} \partial {S_{i\min }}{\rm{/}}\partial \Delta {U_{ij}} \gg \partial {S_{i\min }}{\rm{/}}\partial {U_i} \\ \partial {S_{j\min }}{\rm{/}}\partial \Delta {U_{ij}} \gg \partial {S_{j\min }}{\rm{/}}\partial {U_j} \\ \end{gathered} \right.$$ (12) Simin、Sjmin作为功率域${\tilde S_{iPQL}}$、${\tilde S_{jPQL}}$的大小量化指标，由ΔUij主导确定，即近似有：
$$\left\{ \begin{gathered} {S_{i\min }} \propto \Delta {U_{ij}} \\ {S_{j\min }} \propto \Delta {U_{ij}} \\ \end{gathered} \right.$$ (13) 以长40km的220kV等级LGJ-400型线路为例，线路端电压、压差对末端功率域大小的影响如图 5所示。可见，Ui、Uj的正常波动对功率域影响很小，ΔUij才是决定功率域大小的主导因子。故工程计算可忽略Ui、Uj正常波动的影响。
![]()
图 5 简单模型线路功率域的压差主导因子Figure 5. Leading factor of voltage difference in power domain of simple model line下面分析传统工程简化算法(即式(4))在线路压差计算时的可靠性。
由式(11)可得：
$$\Delta {U_{ij}} = \frac{{{\rm{|}}{Z_L}{\rm{|}}{S_{j\min }}}}{{{U_j}}}$$ (14) 由式(4)可得：
$$\Delta {U_{ij}} \approx \frac{{{\rm{|}}{Z_L}{\rm{|}}{S_j}\cos (\alpha - \varphi )}}{{{U_j}}} = \frac{{{\rm{|}}{Z_L}{\rm{|}}{S_{jl}}}}{{{U_j}}}$$ (15) 式中：Sj、$ \varphi $分别为线路末端复用率${\bar S_j}$的视在功率和功率因数角; Sjl为${\bar S_j}$在直线l上的投影长度。
将Sjl标注在图 4中。可见：Sjl < Sjmin，即式(4)求得的ΔUij明显偏小。当线路的阻抗角α和末端cos$ \varphi $都较大时，|Sjmin-Sjl|增大，将导致式(4)的ΔUij计算偏差太大，根本无法使用。
2.3 ∏型线路模型的功率域及其特性
长线路和电缆的容性特征不能忽略。下面采用图 6所示的∏型模型，分析影响功率安全域大小的主导因子。
文献[21]给出了该模型首、末端功率域边界的圆弧曲线分别为：
$$\left(P_{i}-\frac{{U_{i}}^{2} R_{L}}{\left|Z_{L}\right|^{2}}\right)^{2}+\left[Q_{i}-U_{i}{ }^{2}\left(\frac{X_{L}}{\left|Z_{L}\right|^{2}}-\frac{B_{L}}{2}\right)\right]^{2}=\left(\frac{U_{i} U_{j}}{\left|Z_{L}\right|}\right)^{2}$$ (16) $${({P_j} + \frac{{U{{_j^{}}^2}{R_L}}}{{{\rm{|}}{Z_L}{{\rm{|}}^2}}})^2} + {[{Q_j} + U_j^2(\frac{{{X_L}}}{{{\rm{|}}{Z_L}{{\rm{|}}^2}}} - \frac{{{B_L}}}{2})]^2} = {(\frac{{{U_i}{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}})^2}$$ (17) 设该模型线路正常承载，下面以末端功率域为例，分析其大小与压差的关系。
末端域的大小指标为
$${S_{j\min }} = \frac{{{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}}({U_i} - {U_j}\sqrt {1 - {X_L}{B_L} + \frac{1}{4}B_L^2{\rm{|}}{Z_L}{{\rm{|}}^2}} )$$ (18) 式(18)可写成：
$${S_{j\min }} = \frac{{{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}}({U_i} - a{U_j})$$ (19) 式中：$a = \sqrt {1 - {X_L}{B_L} + \frac{1}{4}B_L^2{\rm{|}}{Z_L}{{\rm{|}}^2}} $，只与线路参数和长度相关，故只要线型和长度确定，a便确定。
根据∏模型参数，求得a值如表 1所示。由表 1可见，一般架空长线或电缆的a都略小于1。故∏模型与简单模型的灵敏度特性相似。
表 1 ∏型模型线路a值Table 1. a value of ∏-type model line电压等级/kV 线路型号 线路长度/km a 10 YJV22-3×120 10 0.9995 110 LGJ-300 100 0.9943 220 LGJ-400 200 0.9772 220 LGJ-2×400 200 0.9775 500 LGJ-4×500 400 0.9125 500 LGJ-4×500 500 0.8645 以长200km的220kV等级LGJ-400型线路为例，Sjmin对端电压和压差的灵敏度如图 7所示。可见，考虑线路容性后，线路的压差约束，仍然是其功率域大小的主导因子。
![]()
图 7 ∏型线路功率域的压差主导因子Figure 7. Leading factor of voltage difference in power domain of ∏-type model line综上所述，线路功率域的大小由线路压差主导确定。故将正常运行时允许的压差范围对应的线路首、末端功率域，称为线路“负荷安全域”[21]。只要功率在安全域内，线路压差便在安全范围内。
3. 多级电网静态功–角稳定的路径功角约束
电网的静态功–角稳定性，可认为是有功从电源到实际低压负荷的同步传输特性及能力，其充要条件是：每条有功路径都满足静态功–角稳定[26]。故关键问题是搞清有功路径允许的大致极限功角(即路径的极限相位角差)。
有功都是从电源经电网流向负荷，无论电网拓扑如何，不会形成功率环流。故可由负荷节点开始，沿着有功方向，逆向搜索直至关联电源而得到有功路径。以图 8(a)多级局部电网为例。图 8(b)中，负荷F4与电源的关联路径，可由图 8(a)中的流经线路进行等相位差拆分(即看成并联拆分)得到。
线路拆分不影响阻抗角，假设发电机励磁调节可维持内电势${E'_q}\angle 0$恒定。下面估算多级有功路径的允许功角范围。
1) 若多级路径中没有(站内)无功补偿。
末端的功率–电压关系如图 3(a)中的末端曲面所示。可见，在电压稳定的上半曲面中，随着末端功率的增长，末端电压加速递减，故单机–无功大系统模型并不适用此情况下的路径功–角特性分析。
采用戴维南等值模型较为合适，设其等值线路的阻抗、电抗和阻抗角分别为ZE、XE和αE。假设路径末端负荷为纯有功，即末端Qj=0，根据式(8)，可得末端电压为
$${U_j} = \frac{{{{E'}_q}\sin (\alpha - {\theta _j})}}{{\sin {\alpha _E}}}$$ (20) 根据式(20)、(7)，可得末端的功–角关系为
$${P_j} = \frac{{{{E'}_q}^2}}{{{\rm{|}}{Z_E}{\rm{|}}}}(\frac{{\sin 2({\alpha _E} - {\theta _j})}}{{2\sin {\alpha _E}}} - \frac{{{{\sin }^2}({\alpha _E} - {\theta _j}) \cdot \cos \alpha }}{{{{\sin }^2}{\alpha _E}}})$$ (21) 式(20)、(21)的特性如图 9所示。若不计电阻，令αE=90°，式(21)可简化为
$${P_j} = \frac{{{{E'}_q}^2}}{{{X_E}}}\frac{{\sin (2{\theta _j})}}{2}$$ (22) 由图 9及式(22)可见，在没有无功补偿的情况下，多级有功路径(含发电机内支路、变压器支路和线路)的静态功–角稳定极限功角都不超过45°。
这是因为在向感性支路末端输送有功时，首端都需要较大无功，且随有功负荷增大加速递增。如图 3(b)所示，线路的首、末端功率圆弧呈“喇叭口”形状。所以，若没有无功补偿，多级电网根本无法维持电压安全水平，也无法传输较大的有功。
2) 若路径中无功补偿能够维持正常电压。
只有在无功补偿能够维持电压安全水平的情况下，讨论多级路径的静态功–角稳定极限问题才有实际意义。若末端Uj为不变，参照式(7)，令：
$$\frac{{\partial {P_j}}}{{\partial {\theta _j}}} = \frac{{E'{U_j}}}{{{\rm{|}}{Z_L}{\rm{|}}}}\sin (\alpha - {\theta _j}) = 0$$ (23) 由式(23)可知，从发电机到实际负荷的多级有功路径，其静态极限功角等于路径阻抗角α，略小于90°。一般电压等级越低，线路的α变小，不同线型的路径功–角特性如图 10所示。
实际电网中，每条有功路径一般是由4—6个电压等级的多种型号线路和变压器支路串联而成。由于高压架空线长度占比较大，再考虑到发电机、变压器内支路都几乎为电抗支路，故多级有功路径的综合阻抗角仍较大，一般为80°左右。
发电机正常运行时，内转子角大概在30°左右。故可估多级有功路径(只含线路和变压器支路)的极限功角大致为50°左右。
4. 线路负荷安全域内的有功路径功角特性
4.1 允许压差(安全域)对应的单级路径最大功角
在压差约束下，当线路末端功率沿对应功率域的圆弧边界变化时，由式(7)、(8)可得相应的线路功角为
$${\theta _{ij}} = \alpha - \arctan \frac{{{Q_j}{\rm{|}}{Z_L}{\rm{|}} + U{{_j^{}}^2}\sin \alpha }}{{{P_j}{\rm{|}}{Z_L}{\rm{|}} + U{{_j^{}}^2}\cos \alpha }}$$ (24) 由式(24)可见，域内(包括边界)最大功角θijmax对应着Qj=0且Pj最大的末端功率点，如图 11中的B点。此时，首端的对应功率点B′点。
以60km的220kV等级的LGJ-400/50线型为例。取压差为0.1pu、0.2pu，可得到对应的末端功率域圆弧边界。当末端复功率沿边界变化时，线路功角变化如图 12所示。
![]()
图 12 LGJ-400/50线路θijmax与末端功率域边界的关系Figure 12. Relationship between the maximum power angle of LGJ-400/50 line and the end power domain boundary故令Qj=0，分别代入式(9)、(24)，可得到末端功率域内的最大有功Pjmax及θijmax，分别为
$${P_{j\max }} = \frac{{{U_j}\sqrt {U_i^2 - U_j^2{{\sin }^2}\alpha } - U_j^2\cos \alpha }}{{{\rm{|}}{Z_L}{\rm{|}}}}$$ (25) $${\theta _{ij\max }} = \alpha - \arcsin [(1 - \frac{{\Delta {U_{ij}}}}{{{U_i}}})\sin \alpha ]$$ (26) 下面分析线路功率域内θijmax的其他特性：
1) 当线型(即阻抗角α)确定后，θijmax的主导相关因子是线路压差。
式(26)中的ΔUij/Ui类似为压差的标幺值，由灵敏度分析可得
$${\rm{|}}\frac{{\partial (\Delta {U_{ij}}{\rm{/}}{U_i})}}{{\partial \Delta {U_{ij}}}}{\rm{|/|}}\frac{{\partial (\Delta {U_{ij}}{\rm{/}}{U_i})}}{{\partial {U_i}}}{\rm{|}} = \frac{{{U_i}}}{{\Delta {U_{ij}}}} \gg 1$$ (27) 故当线路压差约束给定后，θijmax就基本确定了。这与前述的“线路压差主导确定功率域”的分析结论是吻合的。
仍以220kV等级的LGJ-400/50线型为例。根据式(26)，θijmax与ΔUij的关系如图 13所示。可见，近似为线性递增关系，即近似有：
$${\theta _{ij\max }} \propto \Delta {U_{ij}}$$ (28) ![]()
图 13 LGJ-400/50线型θijmax与压差的关系Figure 13. Relationship between the maximum power angle of LGJ-400/50 line and voltage difference2) 给定线路压差约束后，阻抗角α越大的线型，则θijmax越大。
证明：由式(26)可得：
$$\frac{{\partial {\theta _{ij\max }}}}{{\partial \alpha }} = 1 - \frac{{k\cos \alpha }}{{\sqrt {1 - {{(k\sin \alpha )}^2}} }} > 0$$ (29) 式中$k = 1 - \Delta {U_{ij}}{\rm{/}}{U_i}$。故α、θijmax趋势相同。
若给定线路压差为0.1pu，根据式(27)，θijmax与α的关系如图 14所示。可见，θijmax(α)基本不受首端Ui的影响，但随α非线性增大。
电压等级越高的线路，一般α较大，故θijmax也较大。
3) 当线型和压差约束确定后，θijmax与线路长度无关。
由式(26)可见，θijmax与线路阻抗模值|ZL|无关。从另一个角度看，当ΔUij给定后，某线型的线路越长，则功率域就越小(参见式(12))，所以域内的θijmax不变。
将各级电网中的有功路径称为单级路径。结合以上分析，还可推理出：在线型一致的各级电网中，无论拓扑形式和潮流方向如何，只要各节点电压都处于安全水平，则单级路径的功角，都不会超过安全压差对应的θijmax。
以图 15所示的某等级环网拓扑为例。在图 15(b)中，令线路压差ΔU35、ΔU52对应的最大功角分别为θ35max、θ52max，故有：
$$\left\{ \begin{gathered} \Delta {U_{32}} = \Delta {U_{35}} + \Delta {U_{52}} \\ {\theta _{32\max }} = {\theta _{35\max }} + {\theta _{{\rm{52}}\max }} \\ \end{gathered} \right.$$ (30) 只要ΔU32在允许范围内，根据式(28)，串联路径3-5-2的功角不会超过其最大功角θ32max。分析可见，只要环网节点5、3、2的电压都在安全水平，则无论是串联3-5-2、5-3-2，还是单线路3-2、5-3的单级路径，压差都在允许范围，功角都不会超过对应的最大功角。
综上所述，线型给定后，线路的压差约束、功率域大小和最大功角，三者对应且呈近似正比关系; 在各等级电网内，其内单级路径的最大功角取决于压差约束。
4.2 允许压差(安全域)对应的多级路径最大功角
设多级路径由各级线路串成。不同电压等级允许的线路压差范围如表 2所示。根据式(27)可以得到各等级不同型号线路的安全域内的最大功角θijmax。叠加可以得到多级路径的最大功角，如表 3所示。
表 2 各电压等级允许的线路安全压差范围Table 2. Allowable range of safe voltage difference for each voltage level电压等级/kV 首端电压范围/pu 末端电压范围/pu 允许压差范围/pu 550 1.1~1.0 1.05~0.95 0.15 220 1.1~1.0 1.05~0.95 0.15 110 1.07~0.97 1.05~0.95 0.12 10 1.07~1.0 1.07~0.93 0.14 表 3 各电压等级不同线型的功率域内最大功角Table 3. Maximum power angle in power domain with different line types of each voltage level电压等级(线型) 线路参数/ (Ω/km) θijmax/(°) (ΔUij= 0.15pu) θijmax/(°) (ΔUij= 0.2pu) θij/(°)(ΔUij=0.15pu) θij/(°)(ΔUij=0.2pu) cos $ \varphi $ =0.9 cos$ \varphi $=0.95 cos$ \varphi $=0.95 10kV (LGJ-120) 0.27+ j0.335 8.9 11.6 3.6 — 6.6 110kV (LGJ-300) 0.105+ j0.379 18.2 22.5 8.2 — 13.4 220kV (LGJ-400) 0.078+ j0.402 21.0 25.9 — 11.9 15.3 500kV (LGJ-4×500) 0.016+ j0.277 29.2 33.7 — 15.0 19.0 多级路径最大功角/(°) — 77.3 93.6 38.7 54.3 由表 3可见，在允许的压差内，若各电压等级都达到安全域内的最大功角，则多级有功路径(还未包括变压器支路)最大功角将超过70°，静态功–角稳定裕度是不够的。
5. 满足功–角稳定的线路负荷安全域修正
实际上，有功路径中的线路一般不会同时达到最大功角。更主要的是，线路末端cos$ \varphi $一般略小于1，使线路、有功路径的实际功角变小。
下面结合功率因数的允许范围，针对各级电网中的单线路径、串联路径，分别阐述线路负荷安全域的修正方法。
1) 某电压等级中的单线路径。
由式(7)、(8)可得：
$$\frac{{{U_i}\cos (\alpha - {\theta _{ij}}) - {U_j}\cos \alpha }}{{{U_i}\sin (\alpha - {\theta _{ij}}) - {U_j}\sin \alpha }} = \tan \varphi $$ (31) 根据式(31)，令Ui=1.1pu、ΔUij=0.15pu，在不同电压等级、线型对应的线路末端功率域的圆弧边界上，θij与cos $ \varphi $的关系如图 16所示。可见，当末端功率因数略小于1时，线路功角快速衰减。
![]()
图 16 末端功率域边界上功率因数与功角的关系Figure 16. Relationship between power factor and power angle on the end power domain boundary若cos$ \varphi $分别为0.9、0.95，线路及有功路径的功角如表 3所示。可见，在ΔUij=0.15pu对应的功率域内，根据cos$ \varphi $的允许范围，对负荷安全域进行修正后，多级有功路径(未含变压器支路)的最大功角为38.7°，在安全范围内。
负荷安全域修正如图 17所示，即原负荷安全域o-C-B-o，被切除尖角区域D-B-D1。
2) 某电压等级中的串联路径。
可采用以下2种方法得到线路功率约束。
一种方法是：以串联路径的总长度、允许压差，得到路径的负荷安全域; 再根据允许的最小功率因数，进行修正以切除尖角区域，得到串联路径中的线路负荷安全域。该方法的特点是，单级串联路径中的线路无差别对待，方法简单，但导致前部线路的功率约束区域太小。
另一种方法是：根据路径分流情况，在路径压差限制范围内，修正单级串联路径中各线路的允许压差，得到各线路的负荷安全域，并利用功率因数进行修正。
6. 分散负荷安全域的研究路径
综上所述，为兼顾多级电网的静态电压安全和功–角稳定性，线路负荷安全域的研究路径如图 18所示。
![]()
图 18 电压安全和功–角稳定的分散负荷安全域研究路径Figure 18. Research path of distributed load security domain of voltage safety and power-angle stability研究得到的分散负荷安全域，可作为整体优化控制和电网规划的分散功率约束条件，还用于分散安全控制。下面针对分散控制举例分析。
7. 基于线路负荷安全域的全网分散控制
7.1 电网静态电压安全的分散控制
站内无功补偿的作用可视为补偿上级线路(即站内进线)的末端无功负荷。
根据多级电网的电压“锯齿”分布特征，提出一种站内电压分散控制策略：1)在每个降压变电站内，先通过无功补偿控制，将进线负荷“拉入”负荷安全域，以限制好压差; 2)再调节变比，调好出线电压(前半齿)，便可将全网电压的锯齿分布保持在正常范围，即电压安全水平。
其中，压差控制是关键，基于进线(末端)的负荷安全域，可进行无功补偿的量化控制。设该线路的最大压差允许值为0.15pu，对应的末端负荷安全域边界如图 17中的圆弧$ \stackrel{⌢}{CD}$。若该线路末端实际负荷为M2点，则补偿量Qc的范围应为
$${Q_{M2}} - {Q_M} \leqslant {Q_c} \leqslant {Q_{M2}}$$ (32) 如图 19所示，通过无功补偿，将运行点拉进安全域内，可使上级线路压差维持在允许的安全范围内，且补偿后无功不会倒流进该线路。
7.2 电网静态功–角安全的分散有功限制
传统的热稳定校验与线路长度无关。通过热稳定校验的长线路，很可能压差超限，也可能导致路径功角超限。
为保证电网静态电压和功–角安全性，线路末端负荷应在其安全域内(图 19所示)。故线路有功负荷必须限制，限额为图 19中D1点的有功。
有功限额与线路型号和长度都密切相关。设无功补偿后线路末端的功率因数为cos$ \varphi $，将Qj=Pjtan$ \varphi $代入功率域边界的式(9)，可得：
$${P_j} = \frac{{\sqrt b - (\cos \alpha + \sin \alpha \tan \varphi )U_j^2}}{{(1 + {{\tan }^2}\varphi )\sqrt {r_0^2 + x_0^2} L}}$$ (33) 式中：
$$\begin{gathered} b = U_j^4{(\cos \alpha + \sin \alpha \tan \varphi )^2} - \; \\ \;\;\;\;\;{\rm{(}}1 + {\tan ^2}\varphi {\rm{)(}}U_j^4 - U_i^2U_j^2{\rm{)}} \\ \end{gathered} $$ (34) 式中：r0、x0为1km线路的电阻、电抗; L为线路长度。
根据表 2中的最大允许压差和表 3中的线路参数，将$ \varphi $=0、$ \varphi $=arccos0.95或$ \varphi $=arccos0.9分别代入式(33)、(34)，可得的线路有功限额与线长的关系，如图 20所示。
![]()
图 20 不同线型的末端有功限额与线长的关系Figure 20. Relationship between terminal active power limit and line length of different lines若是单级串联路径，可参照前面的方法，修正减小线路的有功限额。
当线路较短时，由安全域得到的有功限额有可能大于传统的热稳定、动稳定限额。实际应用时，应以最小限额为准。
8. 算例分析
以附图A1所示的IEEE 39节点系统为例。美国新英格兰输电网的电压等级为765kV、345kV(230kV)、138kV，IEEE 39节点系统是该州的一个345kV电网，其中39号机是相连的加拿大电网等值机。
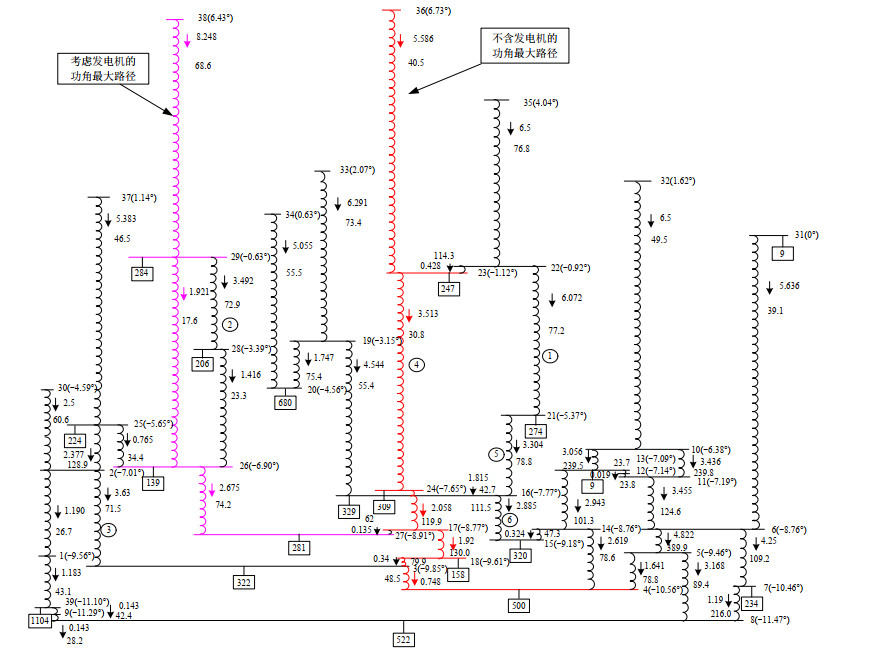
针对IEEE 39节点系统的一个典型潮流断面，文献[23]给出了相应的映射弹性网映模型，如附图A2所示。该潮流断面的发电机、变压器和线路功角如附表A1—A3所示。可见，该345kV等级电网潮流中，功角最大的线路、路径功角(含变压器支路)分别为：
1) l23-24：6.53°;
2) L36-23-24-16-17-18-3-4：17.29°。该路径经过7条线路，在附图A1—A2中标红色。
若再包括发电机功角，根据附表A1和附图A2，最大路径功角为L发电机-38-29-26-27：49.97°。在附图A2中标粉红色。
下一级的138kV电网中，路径功角一般比345kV电网中的小。估计从发电机(含发电机内支路)到138kV母线为止，所有路径中的最大功角不超过65°。在该潮流分布下，全网应能满足静态功–角稳定的要求。
对比附图A1、A2可见，文献[24]给出的映射弹性网模型直观展现了电网的有功路径及其功角。
若采用文献[26]的安全优化方法，优化机组出力，得到新的潮流分布下的映射弹性网，如附图A3所示。可见，优化后的所有路径功角接近，且最大路径功角明显变小，提高了电网的功–角安全性。
9. 说明
1) 虽然实际500kV环网较长，但一般起着“大母线”作用，有功路径并不一定较长，故未采用长线路模型，只考虑了简单阻抗模型和∏型模型。
2) 计及各变压器支路后，安全域内修正后的多级有功路径最大功角可能达到60°左右，考虑发电机内转子角后，比较危险。但实际线路不太可能同时达到域内最大功角，如此设定局部功率约束是可行的。
3) 工程中，经稳定校验，线路有功限额一般取理论极限功率(功角90°)的1/5、1/4、1/3，对应功角分别为11.5°、14.5°、19.5°。与表 3基本吻合，相互印证了合理性。
4) 根据文中分析，增加1000kV等级特高压交流后，需缩小线路功率约束区域。这也是相比特高压直流，点对点远距离重载输电能力较弱的原因。但特高压交、直流各有特点，关键是应该深入研究在电网中的应用形态和方法。另外，针对不同负荷密度地区，采用相同的电压等级递进方式，会导致高密度区域的电网过于密集，故应研究不同递进方式的电网安全和经济性。本文所提思路和方法，可用于这些事关电网发展的重大课题研究。
10. 结论
线路的压差、功角都与功率相关。为维持多级电网的电压安全水平，并满足全网静态功–角静态稳定要求，针对局部功率约束问题进行了研究。研究发现：
1) 多级电网的电压幅值呈“锯齿波”分布特征; 维持全网电压安全水平的关键，是限制所有线路的压差。只要线路负荷在以功率圆为边界的安全域内，压差便在正常允许范围内。
2) 线型确定后，线路允许压差、负荷安全域大小、安全域内最大功角，三者对应且近似呈正比关系。
3) 在各级电网中，无论何种拓扑形式，其内有功路径的最大功角取决于该级电网内的允许压差。
4) 为满足多级电网静态功–角稳定，多级有功路径的极限功角(含发电机功角)等于综合阻抗角，略小于90°，大约为80°左右。
5) 线路负荷安全域虽然可约束压差，但域内最大功角，将导致多级有功路径的功角超限。
因此提出了各等级内安全域的修正方法：考虑功率因数的允许范围，切除安全域的尖角区域; 针对串联路径，采用串联阻抗或分配线路限制压差等方法，缩小安全域的圆弧边界。
基于上述特征，提出了电网分散安全控制策略：通过无功补偿和限制有功，将所有的线路负荷都限制在修正后的安全域内。
研究给出了线路分散负荷安全域及其理论依据。作为兼顾满足电网电压安全和静态功–角稳定的局部功率约束条件，可广泛应用于全网优化控制、分散安全控制和网架、无功规划等方面，具有较大的工程应用价值。
附录A
![]()
A1 新英格兰10机39节点系统及功角最大的有功路径A1. New England 10-machine 39-node system and the active path with the largest power angle![]()
A2 39节点系统的映射弹性网及功角最大有功路径A2. Mapping elasticity network of the 39-node system and the active path with the largest power angleA1 IEEE 39节点系统的发电机功角A1. Generator power angle of IEEE 39 node system节点号 30 31 32 33 34 35 36 37 38 39 发电机功角/(°) 0.07 22.8 22.43 19.66 32.78 21.80 22.34 20.60 34.63 -7.22 A2 IEEE 39节点系统的线路功角A2. Line power angle of IEEE 39 node system线路编号 24-23 26-29 16-19 21-22 26-28 2-3 28-29 2-1 16-21 6-7 5-8 26-27 功角/(°) 6.53 6.27 4.63 4.45 3.51 2.85 2.76 2.56 2.41 2.22 2.02 2.01 线路编号 4-14 14-13 6-11 1-39 16-15 25-2 25-26 4-5 17-16 18-17 3-4 11-10 功角/(°) 1.89 1.68 1.55 1.53 1.40 1.35 1.26 1.21 1.0 0.84 0.79 0.73 线路编号 5-6 13-10 7-8 15-14 3-18 23-22 39-9 9-8 27-17 16-24 — — 功角/(°) 0.71 0.62 0.51 0.44 0.24 0.20 0.19 0.17 0.14 0.12 — — A3 IEEE 39节点系统的变压器支路功角A3. Transformer branch power angle of IEEE 39 node system变压器支路 31-6 32-10 36-23 38-29 37-25 33-19 34-20 35-22 30-2 功角/(°) 8.76 8.0 7.86 7.06 6.79 5.22 5.19 4.96 2.42 ![]()
A3 39节点系统安全优化后的映射弹性网A3. Security-optimized mapping elasticity network of the 39-node system -
![]()
图 1 多级电网节点电压的锯齿分布特征
Figure 1. Sawtooth distribution feature of node voltage in multi-level power grid
![]()
图 3 首、末端功率圆曲线及负荷安全域
Figure 3. Power circular curve and load security domain at the head and end of the line
![]()
图 5 简单模型线路功率域的压差主导因子
Figure 5. Leading factor of voltage difference in power domain of simple model line
![]()
图 7 ∏型线路功率域的压差主导因子
Figure 7. Leading factor of voltage difference in power domain of ∏-type model line
![]()
图 12 LGJ-400/50线路θijmax与末端功率域边界的关系
Figure 12. Relationship between the maximum power angle of LGJ-400/50 line and the end power domain boundary
![]()
图 13 LGJ-400/50线型θijmax与压差的关系
Figure 13. Relationship between the maximum power angle of LGJ-400/50 line and voltage difference
![]()
图 16 末端功率域边界上功率因数与功角的关系
Figure 16. Relationship between power factor and power angle on the end power domain boundary
![]()
图 18 电压安全和功–角稳定的分散负荷安全域研究路径
Figure 18. Research path of distributed load security domain of voltage safety and power-angle stability
![]()
图 20 不同线型的末端有功限额与线长的关系
Figure 20. Relationship between terminal active power limit and line length of different lines
![]()
A1 新英格兰10机39节点系统及功角最大的有功路径
A1. New England 10-machine 39-node system and the active path with the largest power angle
![]()
A2 39节点系统的映射弹性网及功角最大有功路径
A2. Mapping elasticity network of the 39-node system and the active path with the largest power angle
![]()
A3 39节点系统安全优化后的映射弹性网
A3. Security-optimized mapping elasticity network of the 39-node system
表 1 ∏型模型线路a值
Table 1 a value of ∏-type model line
电压等级/kV 线路型号 线路长度/km a 10 YJV22-3×120 10 0.9995 110 LGJ-300 100 0.9943 220 LGJ-400 200 0.9772 220 LGJ-2×400 200 0.9775 500 LGJ-4×500 400 0.9125 500 LGJ-4×500 500 0.8645 
下载: 导出CSV
表 2 各电压等级允许的线路安全压差范围
Table 2 Allowable range of safe voltage difference for each voltage level
电压等级/kV 首端电压范围/pu 末端电压范围/pu 允许压差范围/pu 550 1.1~1.0 1.05~0.95 0.15 220 1.1~1.0 1.05~0.95 0.15 110 1.07~0.97 1.05~0.95 0.12 10 1.07~1.0 1.07~0.93 0.14
下载: 导出CSV
表 3 各电压等级不同线型的功率域内最大功角
Table 3 Maximum power angle in power domain with different line types of each voltage level
电压等级(线型) 线路参数/ (Ω/km) θijmax/(°) (ΔUij= 0.15pu) θijmax/(°) (ΔUij= 0.2pu) θij/(°)(ΔUij=0.15pu) θij/(°)(ΔUij=0.2pu) cos φ =0.9 cosφ=0.95 cosφ=0.95 10kV (LGJ-120) 0.27+ j0.335 8.9 11.6 3.6 — 6.6 110kV (LGJ-300) 0.105+ j0.379 18.2 22.5 8.2 — 13.4 220kV (LGJ-400) 0.078+ j0.402 21.0 25.9 — 11.9 15.3 500kV (LGJ-4×500) 0.016+ j0.277 29.2 33.7 — 15.0 19.0 多级路径最大功角/(°) — 77.3 93.6 38.7 54.3
下载: 导出CSV
A1 IEEE 39节点系统的发电机功角
A1 Generator power angle of IEEE 39 node system
节点号 30 31 32 33 34 35 36 37 38 39 发电机功角/(°) 0.07 22.8 22.43 19.66 32.78 21.80 22.34 20.60 34.63 -7.22
下载: 导出CSV
A2 IEEE 39节点系统的线路功角
A2 Line power angle of IEEE 39 node system
线路编号 24-23 26-29 16-19 21-22 26-28 2-3 28-29 2-1 16-21 6-7 5-8 26-27 功角/(°) 6.53 6.27 4.63 4.45 3.51 2.85 2.76 2.56 2.41 2.22 2.02 2.01 线路编号 4-14 14-13 6-11 1-39 16-15 25-2 25-26 4-5 17-16 18-17 3-4 11-10 功角/(°) 1.89 1.68 1.55 1.53 1.40 1.35 1.26 1.21 1.0 0.84 0.79 0.73 线路编号 5-6 13-10 7-8 15-14 3-18 23-22 39-9 9-8 27-17 16-24 — — 功角/(°) 0.71 0.62 0.51 0.44 0.24 0.20 0.19 0.17 0.14 0.12 — —
下载: 导出CSV
A3 IEEE 39节点系统的变压器支路功角
A3 Transformer branch power angle of IEEE 39 node system
变压器支路 31-6 32-10 36-23 38-29 37-25 33-19 34-20 35-22 30-2 功角/(°) 8.76 8.0 7.86 7.06 6.79 5.22 5.19 4.96 2.42
下载: 导出CSV
-
[1] KUNDUR P, PASERBA J, AJJARAPU V, et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1387-1401. DOI: 10.1109/TPWRS.2004.825981
[2] VOURNAS C D, SAUER P W, PAI M A. Relationships between voltage and angle stability of power systems[J]. International Journal of Electrical Power & Energy Systems, 1996, 18(8): 493-500. http://www.sciencedirect.com/science/article/pii/0142061596000099
[3] 韩文, 韩祯祥. 电压崩溃与功角不稳的关系[J]. 电力系统自动化, 1996, 20(12): 16-19. HAN Wen, HAN Zhenxiang. Relationship between voltage collapse and angle instability[J]. Automation of Electric Power Systems, 1996, 20(12): 16-19(in Chinese).
[4] 韩文, 韩祯祥. 一种判别电力系统电压稳定和功角稳定的新方法[J]. 中国电机工程学报, 1997, 17(6): 367-368, 376. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC706.001.htm HAN Wen, HAN Zhenxiang. A new method identifying voltage stability and angle stability[J]. Proceedings of the CSEE, 1997, 17(6): 367-368, 376(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC706.001.htm
[5] 贾宏杰, 余贻鑫, 李鹏, 等. 电力系统混沌现象与不同失稳模式之间的关系[J]. 中国电机工程学报, 2003, 23(2): 1-4. DOI: 10.3321/j.issn:0258-8013.2003.02.001 JIA Hongjie, YU Yixin, LI Peng, et al. Relationships of power system chaos and instability modes[J]. Proceedings of the CSEE, 2003, 23(2): 1-4(in Chinese). DOI: 10.3321/j.issn:0258-8013.2003.02.001
[6] VU H, PRUVOT P, LAUNAY C, et al. An improved voltage control on large-scale power system[J]. IEEE Transactions on Power Systems, 1996, 11(3): 1295-1303. DOI: 10.1109/59.535670
[7] CORSI S, POZZI M, SABELLI C, et al. The coordinated automatic voltage control of the Italian transmission grid-part I: reasons of the choice and overview of the consolidated hierarchical system[J]. IEEE Transactions on Power Systems, 2004, 19(4): 1723-1732. DOI: 10.1109/TPWRS.2004.836185
[8] 林舜江, 袁康龙, 刘明波, 等. 自动电压控制系统对广东电网静态电压稳定性的影响[J]. 电网技术, 2012, 36(6): 102-107. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201206020.htm LIN Shunjiang, YUAN Kanglong, LIU Mingbo, et al. Assessment on influence of AVC system on steady state voltage stability in Guangdong power grid[J]. Power System Technology, 2012, 36(6): 102-107(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201206020.htm
[9] 姜新凡, 严庆伟, 周帆, 等. 基于实时灵敏度分析的湖南电网无功电压优化控制系统[J]. 电网技术, 2004, 28(16): 82-85. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200416018.htm JIANG Xinfan, YAN Qingwei, ZHOU Fan, et al. Optimal automatic voltage control system for Hunan provincial power system based on real-time sensitivity analysis[J]. Power System Technology, 2004, 28(16): 82-85(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200416018.htm
[10] 王为国, 王彬, 郭庆来. 湖北电网无功电压自动控制系统的建设及运行[J]. 湖北电力, 2010, 34(1): 1-3. DOI: 10.3969/j.issn.1006-3986.2010.01.001 WANG Weiguo, WANG Bin, GUO Qinglai. Discussions on problems exiting in construction and operation of reactive-voltage automatic control system in Hubei power grid[J]. Hubei Electric Power, 2010, 34(1): 1-3(in Chinese). DOI: 10.3969/j.issn.1006-3986.2010.01.001
[11] 李端超, 陈实, 吴迪, 等. 安徽电网自动电压控制(AVC)系统设计及实现[J]. 电力系统自动化, 2004, 28(8): 20-22. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT200408005.htm LI Duanchao, CHEN Shi, WU Di, et al. Design and implementation of automatic voltage control (AVC) system for Anhui power grid[J]. Automation of Electric Power Systems, 2004, 28(8): 20-22(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT200408005.htm
[12] 罗曼, 朱磊. 区域电网无功优化控制系统的研究和应用[J]. 电力电容器与无功补偿, 2014, 35(6): 29-34. https://www.cnki.com.cn/Article/CJFDTOTAL-DLDY201406010.htm LUO Man, ZHU Lei. Research and application of reactive power optimization and control system in regional grid[J]. Power Capacitor & Reactive Power Compensation, 2014, 35(6): 29-34(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLDY201406010.htm
[13] YEHIA D M, YOKOMIZU Y, ⅡOKA D, et al. A novel approach to deliverable power in low-voltage DC distribution system on the basis of voltage stability[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2011, 6(5): 395-402. DOI: 10.1002/tee.20675
[14] 赵敏, 安宁, 施浩波, 等. 大型互联电网最大输电能力的自动求解算法[J]. 电网技术, 2012, 36(11): 179-183. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201211031.htm ZHAO Min, AN Ning, SHI Haobo, et al. Algorithm research on automatic calculation of large-scale interconnected power system's total transfer capability[J]. Power System Technology, 2012, 36(11): 179-183(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201211031.htm
[15] 郭琦, 赵晋泉, 张伯明, 等. 一种线路极限传输容量的在线计算方法[J]. 中国电机工程学报, 2006, 26(5): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC200605000.htm GUO Qi, ZHAO Jinquan, ZHANG Boming, et al. A method for on-line computation of total transfer capability[J]. Proceedings of the CSEE, 2006, 26(5): 1-5(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC200605000.htm
[16] 柴旭峥, 梁曦东, 曾嵘. 交流输电线路输送能力曲线计算方法的改进[J]. 电网技术, 2005, 29(24): 20-24. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200524004.htm CHAI Xuzheng, LIANG Xidong, ZENG Rong. An improved calculation method for power-transmitting capability curve of AC transmission line[J]. Power System Technology, 2005, 29(24): 20-24(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200524004.htm
[17] TAYLOR C W. 电力系统电压稳定[M]. 王伟胜, 译. 北京: 中国电力出版社, 2002: 18-27. TAYLOR C W. Power system voltage stability[M]. Wang Weisheng, Trans. Beijing: China Electric Power Press, 2002: 18-27(in Chinese).
[18] 杨帮宇, 彭建春, 何禹清. 功率圆确定稳定约束的可用输电能力分析[J]. 中国电机工程学报, 2008, 28(34): 66-71. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC200834012.htm YANG Bangyu, PENG Jianchun, HE Yuqing. A novel algorithm for calculating available transfer capability using power-circle determine stability constraints[J]. Proceedings of the CSEE, 2008, 28(34): 66-71(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC200834012.htm
[19] North American Electric Reliability Council. Available transfer capability definitions and determination: A reference document prepared by TTC task force[R]. New Jersey: North American Electric Reliability Council, 1996.
[20] 竺炜, 陶琼. 基于电压水平约束的负荷安全域研究方法: 中国, 101944741A[P]. 2011-01-12. ZHU Wei, TAO Qiong. Research methods of load security region based on the voltage level constraint: CN, 101944741A[P]. 2011-01-12(in Chinese).
[21] 竺炜, 凌晨, 张玉龙, 等. 基于电压水平约束的电网负荷安全域[J]. 中国电机工程学报, 2016, 36(23): 6389-6400. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201623010.htm ZHU Wei, LING Chen, ZHANG Yulong, et al. Grid load security domain based on voltage level constraint[J]. Proceedings of the CSEE, 2016, 36(23): 6389-6400(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201623010.htm
[22] 竺炜, 陶琼, 周有庆. 基于弹性力学空间映射的发电机静态功角稳定分析[J]. 中国电机工程学报, 2010, 30(19): 44-50. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201019008.htm ZHU Wei, TAO Qiong, ZHOU Youqing. Generators static power angle stability analysis based on elasticity space mapping[J]. Proceedings of the CSEE, 2010, 30(19): 44-50(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201019008.htm
[23] 竺炜, 周孝信, 唐如. 电网的弹性力学网络拓扑映射[J]. 中国电机工程学报, 2011, 31(31): 109-117. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201131014.htm ZHU Wei, ZHOU Xiaoxin, TANG Ru. Elasticity network topology mapping for power grid[J]. Proceedings of the CSEE, 2011, 31(31): 109-117(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201131014.htm
[24] 竺炜, 周孝信, 蒋頔, 等. 基于映射弹性势能的电网有功承载能力定量指标[J]. 中国电机工程学报, 2014, 34(13): 2088-2099. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201413012.htm ZHU Wei, ZHOU Xiaoxin, JIANG Di, et al. Quantitative index of grid active power load capability based on mapping elasticity potential energy[J]. Proceedings of the CSEE, 2014, 34(13): 2088-2099(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201413012.htm
[25] 竺炜, 刘校锋, 田皓, 等. 主网在线安全态势及运行经验的获取方法[J]. 中国电机工程学报, 2018, 38(22): 6605-6615. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201822013.htm ZHU Wei, LIU Xiaofeng, TIAN Hao, et al. Method of main grid online security situation and operational experience acquisition[J]. Proceedings of the CSEE, 2018, 38(22): 6605-6615(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201822013.htm
[26] 竺炜, 李娟, 蒋银华, 等. 发输电经济及电网安全的综合优化建模方法[J]. 中国电机工程学报, 2015, 35(17): 4335-4344. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201517007.htm ZHU Wei, LI Juan, JIANG Yinhua, et al. Integrated optimization model for generation transmission economic and grid security[J]. Proceedings of the CSEE, 2015, 35(17): 4335-4344(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201517007.htm
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
下载:
