0.   引言

为了提升电力设备的设计制造水平及运行阶段的可靠性，工业生产过程中常采用有限元法分析其内部复杂的电场磁场分布。尤其是随着数字化平台和数字孪生概念^[1-2]的提出，工程实际中需要实时反映设备运行状态。而设备的内部状态，例如温度、应力分布等，是影响其运行性能和寿命的关键因素，这些信息通常无法通过简单的外部观测或场景可视化获得，需要通过有限元法进行多物理场仿真。但有限元法通常需要将计算区域离散化为有限数量的单元，在每个单元内使用有限元理论进行求解。随着计算区域复杂性的增加，计算时间也会随之上升^[3]。因此，在变压器热点温度^[4]、风电场尾流实时计算^[5]等方向，传统有限元法很难做到实时计算，进而无法做到实时评估^[6]。此外，参数设计^[7-8]等方向需要通过有限元法进行多次迭代以完善设计或优化参数。设计师不得不等待每个迭代完成后再进行调整改进，间接导致了次优设计。

部分学者尝试在有限元的求解过程(包括网格剖分^[9]、单元装配^[10]和非线性迭代求解^[11])中采用并行计算方法加快求解速度。但是此类方法的求解速度与图形处理器(graphics processing unit, GPU)算力成正相关，难以部署到实际工程中^[12]。上文所述的实时计算类和设计类问题的参数一般在一定范围内，例如在计算变压器热点温度时，变压器初始温度、线圈的电压等边界条件都是可以预见的，因此代理模型(surrogate model)逐渐成为了近几年的研究热点^[13-14]。代理模型是指在一定参数范围内，首先计算出某些工况下的数值解，然后寻找到一个模型用于计算剩余工况下的解。相较于并行计算，代理模型的通用性更差且需要前置的仿真数据，但其在算力投入和计算速度方面要远远优于并行计算，因此更适合于工程部署。值得注意的是，这里的解是指整个物理场的解，例如电场强度、磁感应强度分布，而不是诸如电机效率、最高温度等衍生的物理量。工业界中，ANSYS公司在流体场计算中率先引入了降阶模型^[15]，COMSOL公司在6.2版本中引入了代理模型模块^[16]。学术界中，本征正交分解(proper orthogonal decomposition, POD)方法被广泛使用^[17-19]。但这些方法在解决几何参数变化问题时的表现一般^[20]。

随着计算机视觉、自然语言处理方向的不断发展，更多学者希望借助神经网络能够拟合任意函数的特性来创建代理模型。文献[21-24]采用U-net卷积神经网络计算电磁场或温度场。然而，不同的网络结构有着不同的归纳偏好^[25]，使用卷积神经网络(convolutional neural networks, CNN)、长短期记忆网络(long short-term memory, LSTM)框架求解物理场问题势必发挥不出其在图像、时间序列处理方面的优势。此外，U-net CNN一般用于特定物理量的计算，例如文献[21, 23]计算的是磁感应强度，若想计算磁场能量或是电磁损耗，则只能先通过近似方法计算导数再算乘积。如果在训练时输入点的个数过少，则会导致近似结果精确度较低。

2021年，文献[26]基于算子的通用近似定理，提出深度算子网络(deep operator network, DeepONet)，其能够在更少的数据集下学习算子，着重考虑了物理场坐标且没有网格点的限制。物理场中，多种工况的计算问题实际上就是计算各种算子。目前DeepONet已经用于求解热传导方程^[27]、流体方程^[28]等，缺乏与工程实际相结合的研究，尤其是在低频电磁场领域中。

本文采用DeepONet框架，提出了一种基于DeepONet的电磁场快速计算方法。首先，根据实际物理模型，使用有限元法对研究对象进行部分预设工况下的建模仿真计算，构建数据集；然后，使用DeepONet进行训练，训练过程中采用自动微分来计算导数，并将导数纳入到损失函数中，通过训练好的模型实现研究对象所有预设工况下的快速计算；最后，将该方法和U-net系列进行比较，通过总体误差对比、逐点误差分布来阐述不同网络的特点，说明DeepONet相较于有限元法具有更快的求解速度；可以通过磁矢势和电势计算多个衍生物理量，相较于其他网络更易于后处理。

1.   DeepONet算法原理

1.1   DeepONet模型

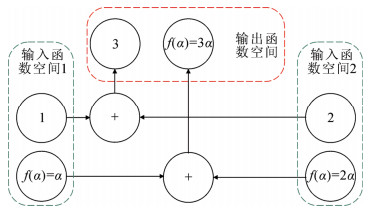
算子表示函数空间到函数空间的映射，例如加减乘除、哈密顿算子等。以加法算子为例，当给定1组函数，例如常函数1、2或函数f(α)=α、f(α)=2α，经过“+”这个算子后，映射到输出函数空间，即常函数3或函数f(α)=3α，如图 1所示。

图  1  加法算子示意图

Figure  1.  Schematic diagram of the addition operator

下载: 全尺寸图片 幻灯片

在物理场中，物理量之间的关系通常由偏微分方程来描述，由边界条件确定解，则变化的边界条件和所要求解的物理量之间可以用1个算子来描述，例如式(1)中的热传导方程。

式中：k_x、k_y是扩散系数；l(x, y)是热源的空间分布；a₁、a₂、a₃、C是常数；s是所要求解的温度分布。在这个方程中，不同的扩散系数、热源分布、所求解的空间域都可以和温度分布形成映射关系，可以用1个算子来表示。

1995年，文献[29]提出了非线性算子的普遍逼近定理，文献[26]在其研究基础上提出并证明了算子的广义逼近定理，即：

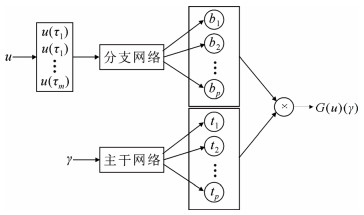
式中：G(u)(γ)表示输入的离散函数空间u到其他函数空间的映射，即算子；g、f表示向量函数；g为数域ℝ^m到ℝ^p的映射，其中ℝ为实数集；f为数域ℝ^d到ℝ^p的映射；ε表示任意 > 0的值； < · > 表示点积。需要强调的是，γ是离散算子G(u)(γ)的采样点，而τ是离散函数u的采样点。由式(2)可知，1个算子可以由很多组输入函数和算子的采样坐标、通过一定的函数运算后作点积运算逼近。基于该定理，Lu等提出了DeepONet框架^[18]，如图 2所示。

图  2  DeepONet结构

Figure  2.  Architecture of DeepONet

下载: 全尺寸图片 幻灯片

DeepONet结构中包含2个网络：分支网络(branch)对应式(2)中的g，主干网络(trunk)对应式(2)中的f；b和t代表映射到数域ℝ^p的向量，作点积运算得到算子G(u)(γ)。在物理场问题中，u可以是方程的初始值、边界值以及源项，γ是算子G(u)(γ)采样点的坐标，甚至可以是随机时间步长^[30]。值得注意的是，分支网络中的τ和主干网络中的γ是2种不同且毫无关联的空间采样点，训练集中每组的γ可以不同。因此，DeepONet从有限数据中学习到的是近似连续的算子，训练完成后，采样点γ可以任意给定，即DeepONet是一种无网格的方法。相较于U-net CNN，DeepONet着重考虑了算子坐标，而U-net CNN学习的是输入输出图像之间的映射，在池化操作中会损失图像中的高频部分，产生钝化模糊的图像块，并丢失位置信息^[31]。此外，正因为DeepONet考虑了坐标，使得其可以通过自动微分^[32] (automatic differentiation, AD)技术来计算偏导，从而通过计算磁矢势或电势来计算磁感应强度或电场强度。

1.2   算法流程

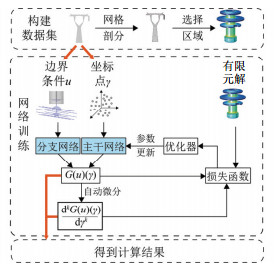
本文提出了一种基于DeepONet的电磁场快速计算方法，首先通过有限元法(finite element method, FEM)求解电磁场问题，再将计算结果导出，构建数据集。之后将边界条件参数送入到分支网络，将坐标送入到主干网络，通过DeepONet框架学习算子，并通过自动微分限制1阶或2阶导数。训练完成后，只需要给定相关的边界条件参数和所需求解的坐标，DeepONet就可以进行快速计算，具体的流程如图 3所示。包括有限元计算、网络训练和结果计算3部分。

图  3  基于DeepONet的快速计算方法流程图

Figure  3.  Rapid calculation method process based on DeepONet

下载: 全尺寸图片 幻灯片

1）构建数据集

本文提出的DeepONet框架属于数据驱动类算法，需要相对精确的数据集。数据可以从实验或是有限元分析中获得，但实验方法往往只能获得部分点的信息，而有限元方法可以获得整个模型的分布图。为了验证DeepONet方法的有效性，本文选择通过有限元计算的方法获得数据。

为获得有限元仿真计算的结果，需要根据研究对象建立其2维或3维的等效几何模型，定义几何模型内各几何区域的材料参数，确定控制方程、边界条件，经过网格剖分后得到刚度矩阵，解线性方程组得到物理场问题的数值解。本文采用COMSOL进行有限元计算。在磁场问题中，导出的数值解应为磁矢势A以及A的各阶导数，考虑到工程实用性，本文在2维问题中导出磁感应强度B的模和∂²A/∂x²+∂²A/∂y²。3维问题中，导出的数值解应为电势V及V的各阶导数，本文在3维案例中导出的是电势V和电场强度E。

工程实际中往往只需要模型的部分区域结果，例如离模型较远距离的空气域电场强度是不重要的，因此可以按照需求选择合适的区域导出数据。

2）网络训练

将有限元计算数据导出为1个数据集。数据集中包括3部分：有限元计算中变化的边界条件、导出网格点坐标、数值解。考虑到在改变模型的情况下，每种边界条件下导出的网格点数量并不相同，导致在训练过程中无法一次送入多种工况，进而导致计算效率大幅下降。因此本文在训练过程中，首先找到所有几何模型中剖分的最大网格点数，然后将其他数据补充第1行数据以达到最大点数。如图 4所示，以2维情况为例，训练集中所有工况中最多剖分了3 210个网格，而某一工况中剖分了3 200个网格，此时需要将该模型导出的所有与网格相关的数据(x、y坐标点，磁矢势，磁感应强度模，尺寸为3 200×4)用第1行数据(尺寸为1×4)补充到3 210。从而使得在计算自动微分时，只是将某一点的误差放大，而不会产生错误的计算结果。值得注意的是，DeepONet是一种无网格的方法，这里补充数据点仅仅是为了加快计算速度，因此在测试集中，由于输入的是一种工况，因此无需补充数据点，这一点会在第3章进行详细说明。

图  4  数据点补充示意图

Figure  4.  Schematic diagram of data point supplement

下载: 全尺寸图片 幻灯片

对于U-net和FCNs网络，由于其输入一般为正方形，因此在数据点需要补充到${\left( {\left[ {\sqrt[t]{n}} \right] + 1} \right)^t}$行，其中n为采样点个数，这里为3 210；t为维度，这里为2维，即t=2；[·]为取整函数，因此需要将数据补充为3 364×4的尺寸，再重塑(reshape)为58×58×4。

文献[33]从多个角度分析了物理信息神经网络(physics-informed neural networks, PINNs)在电磁场中的应用难点，并提出了多种解决方案。经过实践可知，在主干网络中加入傅里叶特征能够大幅提高计算准确率，且不会造成训练时间的大幅增加。因此本文对主干网络的输入(即xyz坐标)按照式(3)进行傅里叶变换，将输入变换到更高频的特征空间中。

式中：x为神经网络的输入；H为正态分布矩阵，H中的每一列元素服从(0, σ²)的正态分布，σ²为方差。关于σ的选择，可以参考文献[34]，本文中σ取5。由于不同案例中的输入输出不尽相同，因此针对网络其他超参数和具体损失函数的构建，本文将在2.2节和3.2节具体说明。

3）结果计算

使用测试集对DeepONet的泛化性能进行测试。考虑到每个案例中的数据分布并不相同，本文主要采用归一化的平均绝对误差(normalized mean absolute error, NMAE, ${\delta _{{\text{NMAE}}}}$)来衡量，如式(4)所示。相较于平均绝对百分比误差(mean absolute percentage error, MAPE, ${\delta _{{\text{MAPE}}}}$)，NMAE标准可以解决MAPE中真实值为0时所造成的误差为正无穷的情况。而对于真实值不存在0的情况，本文也给出了MAPE误差，如式(5)所示。

式中：${\mathcal{N}_i}$为第i个采样点神经网络输出；${\sigma _{{\text{FEM}i}}}$为第i个采样点数值解。

2.   不同微分约束策略下的网络性能分析

本章以一个简单的例子，探讨了添加微分约束对网络性能的影响。通过分析网络优化过程，从计算时间和结果精度2个维度来评估网络性能。验证微分约束的有效性，并揭示其在提升偏导精度与后处理方面的潜力。该研究可为后续3维静电场的快速计算提供重要参考。

2.1   FEM模型建立

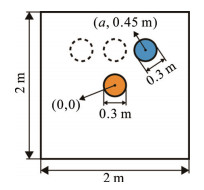
仿真模型如图 5所示。中间圆区域直径为0.3 m，圆心坐标为(0, 0)，电流密度设置为8 000 A/m²；上侧圆的直径为0.3 m，圆心的横坐标a在[−0.5, 0.5] m之间变动，纵坐标保持0.45 m不变；电流密度在[−11, −1] kA/m²之间变动。外部正方形区域边长为2 m。所有区域相对磁导率均为1。最外层边界磁矢势设置为0 Wb/m。网格剖分方面，在2个小圆内部进行细剖，由于上侧圆位置发生了改变，每次剖分的网格数量有所不同，因此按照1.2节的方法补充数据集。每个小圆约有300个网格点，其余地方约有1 450个网格点。

图  5  2维算例几何模型

Figure  5.  Geometric model of 2D cases

下载: 全尺寸图片 幻灯片

等距选取5组横坐标a、6组电流密度b，一共生成5×6=30组数据作为训练集。使用COMSOL Multiphysics 6.2进行计算。

2.2   网络超参数选择及损失函数构建

由于主干、分支网络的作用是找到一个向量函数，使得式(2)成立，因此这2个网络的结构可以任意选择，例如全连接神经网络(full connect neural network, FNN)、CNN等。本文均选择较为简单的FNN结构。优化器均选择Adam。

设定批大小为16，DeepONet分支网络和主干网络的隐藏层均为128个神经元，深度为2，输出层也为128个神经元，如图 6所示。由于需要通过自动微分计算1阶或2阶偏导数，因此激活函数必须是2阶可导，神经网络常见的ReLU函数无法进行训练。本文选择SiLU函数，采用GPU进行训练，显卡为一张NVIDIA RTX A6000。

图  6  2维算例神经网络结构图

Figure  6.  Network structure of 2D cases

下载: 全尺寸图片 幻灯片

本文选择3种策略构建损失函数。第1种是只对磁矢势A进行约束，即训练过程不计算偏导数，注意到2维中磁矢势只有z方向，因此A可以认为是标量；第2种是对A和磁感应强度B的模进行约束，即训练过程中对A求1阶偏导，然后按式(6)计算$\left\| \boldsymbol{B} \right\|$；第3种是对A和源项q进行约束，即训练过程对A求2阶偏导，然后计算∂²A/∂x²+∂²A/∂y²，注意这里即为泊松方程的左端项，其值等于负的磁导率µ×源项。值得一提的是，B只能通过COMSOL进行导出；而源项q是已知的，因此µq也是已知的。例如在中间圆内的µq=4π×10⁻⁷×8 000 Wb/m³，无电流区域为0 Wb/m³，因此这部分区域无需通过COMSOL导出。由于A和B的数量级并不相同，因此本文在偏导损失项前乘一个系数β=0.1，如式(7)所示。2阶偏导同理，取β=0.001。

式中：$\mathcal{L}$为偏导损失；x为神经网络输入坐标向量；$\boldsymbol{\mathcal{N}}$为神经网络输出向量。

2.3   结果分析

图 7为训练集中，磁矢势A和磁感应强度B的模的NMAE值随着训练轮次的变化情况。可以看到在训练过程中，1阶偏导在A的计算上没有显著优势，而在B的计算上具有明显优势。训练集误差从无偏导的5%左右降到0.9%左右。这就好比y=x³和y=x 2个函数，虽然都经过(−1, −1)、(0, 0)、(1, 1) 3个点，但是这3个点的导数并不相同。因此在训练过程中对神经网络进行偏导数的约束是有必要的。2阶偏导约束的训练过程与1阶差距不大，本文将着重分析其计算结果，而非训练过程。

图  7  2维算例中的NMAE随训练轮数变化图

Figure  7.  NMAE varying with training epochs in 2D cases

下载: 全尺寸图片 幻灯片

从训练时间的角度看，无偏导的计算时间为572 s，1阶偏导约束的计算时间为1 799 s，2阶偏导约束的计算时间为3 319 s。可以看到，加入偏导约束后会造成计算时间的增加，计算时间随着偏导阶数的增加而增加。

训练完成后，选择10种非训练集中的工况作为测试集，测试误差如表 1所示。可以看到相较于训练集，测试集的误差要更大。无偏导在B的模和源项上误差都比较大，而1阶偏导能够较好地计算B的模，在源项的计算上仍有不足，2阶偏导对这3项都能达到较好的计算结果。

表  1  2维算例测试集的NMAE对比

Table  1.  NMAE comparison of test sets in 2D cases

参数	NMAE/%
	无偏导	1阶偏导	2阶偏导
A	0.45	0.40	0.76
||B||	6.54	2.12	2.29
−µf	10.3	9.01	5.57

下载: 导出CSV 

| 显示表格

以a=0.27、b=−8.5这组情况为例，3种策略的计算结果及误差图如图 8所示。如图 8中虚线圆中所示，所有策略的误差均集中于位置变动的圆(即图 5中的上侧圆)与周边空气域的位置，这些地方的内外两端源项从8 000 A/m²突然变化到0。文献[34]指出神经网络更倾向于学习平滑的特征而不是突然变化的特征，因此分界面处的信息有待进一步研究。另一方面，如第2行矩形框所示，无偏导的||B||误差还存在于2个圆之间的位置，出现了畸变。而如第5行矩形框所示，无偏导下A的误差主要存在于横坐标[−0.4, 0.4] m之间，纵坐标0.45 m处，正是图 5上侧圆位置变动的地方，这可能是由于网络发生了过拟合，即网络过度拟合于训练集数据。而在另外2种策略中并没有明显的关于变动位置的误差。

图  8  2维算例逐点误差比较

Figure  8.  Comparison of point-by-point errors in 2D cases

下载: 全尺寸图片 幻灯片

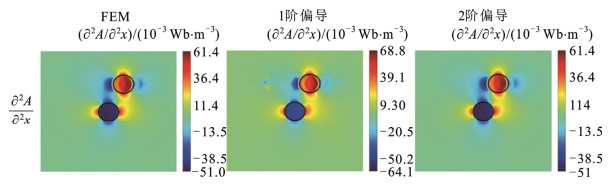
进一步处理数据发现，2阶偏导数的误差主要集中于∂²A/∂x²项，如图 9所示。可以看到2种偏导策略在中心圆部分学习效果较好，而在位置变化的圆上面学习效果较差。因此可以考虑增加训练集数量来改善训练效果。

图  9  ∂²A/∂x²项的计算结果比较

Figure  9.  Comparison of calculation results of ∂²A/∂x² term

下载: 全尺寸图片 幻灯片

综上所述，DeepONet不添加偏导约束时，1阶偏导部分位置会出现畸变，且有过拟合的风险。为DeepONet添加1阶偏导约束时，||B||的计算结果达到预期，然而在∂²A/∂x²项上，采用小训练集对几何变化区域的学习效果不佳。为DeepONet添加2阶偏导约束时，相较于1阶约束，µf的计算结果有一定提升，但同时会造成计算时间的大幅增加。

3.   3维算例分析

复合绝缘子因其独特的气味常遭受到鸟类啄食，啄食后绝缘子性能下降，容易发生电晕现象，需要分析不同缺损程度下的静电场。本章以实际案例鸟啄缺损复合绝缘子为例^[35]，进一步探讨DeepONet在3维静电场中的应用。

3.1   FEM模型建立

缺损复合绝缘子3维模型的具体参数与文献[35]保持一致。本文只展示边界条件部分，如图 10所示。将892.2 kV电压施加于导线和复合绝缘子高压端等位置，对地面、铁塔、复合绝缘子低压端金具等施加0电位。

图  10  绝缘子仿真模型

Figure  10.  Simulation model of the insulator

下载: 全尺寸图片 幻灯片

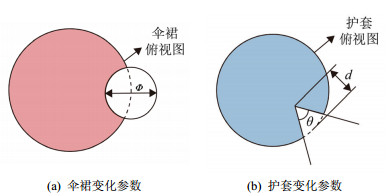
由于该问题主要分析的是伞裙缺损和护套缺损位置的电场强度值，因此本文只导出护套部分和最下端3片伞裙部分，约2 070个网格点。选择的变化参数是伞裙缺损直径Φ、护套缺损深度d和护套缺损角度θ。3个变化参数的具体意义见图 11。

图  11  绝缘子变化参数示意图

Figure  11.  Schematic diagram of the insulator variation parameters

下载: 全尺寸图片 幻灯片

参数的变化范围如表 2所示，等距选取5组Φ、3组d和6组θ，一共5×3×6=150组数据作为训练集。

表  2  绝缘子参数变化范围

Table  2.  Variation range of the insulator parameters

参数	变化范围
Φ/mm	12~20
d/mm	1~3
θ/(°)	20~120

下载: 导出CSV 

| 显示表格

3.2   网络超参数选择及损失函数构建

DeepONet网络隐藏层和输出层神经元个数与第2章保持一致。主干网络的输入从xy变为xyz，分支网络的输入变为3个，设定批大小为8。

由于主要分析的是绝缘子的电势V和电场强度E的模，由第2章分析可知，只需要对电势的1阶偏导数进行计算，因此本文只添加了1阶约束。损失函数如式(7)所示，β=0.1。

为了进一步说明DeepONet的优势，本文将DeepONet与U-net、U-net++进行对比。U-net系列的网络结构与文献[36]保持一致，且输出仅为电场强度E的模。

3.3   结果分析

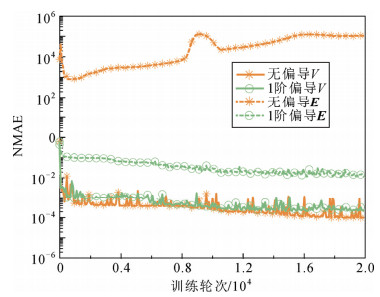
图 12为训练过程中的NMAE曲线，可知无偏导的E的误差很大，说明在3维模型中，如果不对偏导加以约束，则自动微分出来的结果错误。同时，无偏导的V在训练集的误差要低于1阶偏导的V。无偏导的训练时间为860 s，1阶偏导的训练时间为73 min。

图  12  绝缘子NMAE随训练轮数变化图

Figure  12.  NMAE as a function of training epochs in the insulator case

下载: 全尺寸图片 幻灯片

训练完成后，选择10种非训练集中的工况作为测试集，测试误差如表 3所示。可以看到无偏导虽然在电势方面计算更加准确，但是在电场强度模方面计算结果较差。DeepONet的电场强度计算结果要远好于U-net，但略差于U-net++。

表  3  绝缘子算例测试集的NMAE和MAPE对比

Table  3.  NMAE and MAPE comparison of test sets in insulator cases

方法	V(NMAE)/%	V(MAPE)/%	||E||(NMAE)/%	||E||(MAPE)/%
无偏导	0.02	0.02	27.01	28.60
1阶偏导	0.07	0.07	2.23	2.34
U-net	—	—	15.11	15.16
U-net++	—	—	15.10	2.17

下载: 导出CSV 

| 显示表格

以Φ=14 mm、d=1.8 mm、θ=50°为例，1阶偏导DeepONet的计算结果如图 13所示。图 13为散点图，对于DeepONet网络，首先通过COMSOL获得绘图坐标，然后将绘图坐标作为DeepONet主干网络的输入，输出得到每个坐标的计算结果。绘图坐标点有32 768个，借助于DeepONet无网格的优势，可以准确算出每个坐标点解。对于U-net++网络，由于其坐标必须与训练集保持一致，否则效果会大打折扣，因此本文首先导出2 197个网格点，然后通过插值得到绘图网格点。由于无偏导和U-net计算结果较差，因此本文未展示。V的计算结果很好，与FEM几乎没有差别，因此也未展示。

图  13  绝缘子案例逐点误差比较

Figure  13.  Comparison of point-by-point errors in the insulator case

下载: 全尺寸图片 幻灯片

从图 13可以看到，在电场强度模的计算中，U-net++虽然整体误差更低，但最大误差点高于DeepONet。U-net++和DeepONet的误差主要集中于伞裙表面和空气域之间的连接处，与2维一致。

不同网络的计算时间如表 4所示。不同网络的计算时间包括将神经网络模型(.pth文件)加载到python中和将输入数据送入神经网络进行计算并输出结果的时间，DeepONet还包括计算自动微分的时间。可以看到，所有网络的计算时间都在1 s内，远小于有限元法。值得注意的是，训练过程依赖GPU，通常在服务器上完成且无需重复训练；训练完成后部署到实际工程中的计算依靠中央处理器(central processing unit, CPU)，且对硬件没有很高的要求。为证明DeepONet的可部署性，表 4采用个人电脑入门级的CPU(i3 10100)进行计算。

表  4  绝缘子算例在不同网络下的计算时间

Table  4.  Predicted time for the insulators case under different networks

不同网络	FEM	DeepONet	U-net	U-net++
计算时间	45 min	0.598 7 s	0.191 3 s	0.771 3 s

下载: 导出CSV 

| 显示表格

4.   结论

本文提出了一种基于DeepONet的电磁场快速计算方法，以圆形磁场和缺损复合绝缘子静电场计算为例，得到结论如下所述。

1）该方法通过深度算子网络计算磁矢势A和电势V，采用自动微分计算磁感应强度B和电场强度E，相对误差都在3%以下；计算时间均远小于有限元法，复合绝缘子案例中该方法所用时间是有限元法的万分之一。相较于U-net++，该方法的最大误差约为U-net++的1/2且没有网格点的限制，更易于后处理。说明该方法能够在电磁场问题中实现快速、准确的计算。

2）在训练过程中添加偏导约束可以有效提升依赖于计算偏导的物理量(如磁感应强度)的预测精度，但这会导致训练时间延长。工程中需要根据具体情况添加相应的偏导约束。

此外，本文方法并非为了代替传统FEM仿真计算，而是面向设计阶段需要多组参数进行大量计算的情况，例如电池结构优化设计、电机拓扑优化等；或面向设备状态评估实时计算的情况，例如变压器绕组变形等设备内部缺陷的实时评估，实现物理场的快速求解。未来，针对与空气域相接的地方，可以考虑通过优化神经网络架构，进一步提高计算精度。