-
摘要: 高压充油电缆终端的可靠运行是电缆线路稳定运行的前提,但传统充油电缆终端故障诊断模型存在效率低、可靠性差等问题。为准确判断充油电缆终端故障,提出一种最大互信息系数(maximal information coefficient, MIC)结合改进阿基米德算法(improved Archimedes optimization algorithm, IAOA)优化深度置信网络(deep belief network, DBN)的充油电缆终端故障诊断方法。首先,采用MIC理论对电缆终端用硅油中溶解气体浓度的特征量进行降维处理并提取特征量;其次,将优选的特征量作为DBN网络模型的输入,并针对DBN网络超参数选取困难的缺点,提出采用IAOA优化DBN网络模型的超参数;再者,针对AOA算法容易陷入局部最优和搜索能力差等不足,引入多种改进策略优化AOA的方法提高AOA的寻优能力。最后,通过搭建充油电缆终端故障模拟实验平台,收集充油电缆终端故障样本数据并创建类别样本标签,验证了该模型的可行性。实例表明,所提出的诊断方法可以较好地完成故障诊断,测试集的准确率为98.33%。与传统故障诊断模型相比,该方法稳定性好、识别精度高,可为保障高压充油电缆终端的可靠运行提供理论基础。
-
关键词:
- 充油电缆终端 /
- 故障诊断 /
- 最大互信息系数 /
- 改进阿基米德优化算法 /
- 深度置信网络
Abstract: The reliable operation of high-voltage oil-filled cable terminals is a prerequisite for the stable operation of cable lines, but the traditional diagnosis model for oil-filled cable terminal faults has problems such as low efficiency and poor reliability. In order to accurately judge oil-filled cable terminal faults, this paper proposes a fault diagnosis method for oil filled cable terminals based on the maximum mutual information coefficient (MIC) and the improved Archimedes optimization algorithm (IAOA) to optimize the deep trust network (DBN). Firstly, the MIC theory is used to reduce the dimensionality of the dissolved gas concentration in the silicone oil filling agent for cable terminals and perform feature extraction.Secondly, the optimal feature quantity is taken as the input of the DBN network model, and in view of the difficulty in selecting the hyperparameter of the DBN network, the IAOA is proposed to optimize the hyperparameter of the DBN network model. It is easy for the AOA algorithm to fall into local optimization and weak search ability, thus a variety of improvement strategies are introduced to optimize the optimization performance of the AOA method and improve the optimization ability of the AOA. Finally, the feasibility of the model was verified by constructing experimental platform for simulation of oil filled cable terminal faults, collecting fault sample data of oil filled cable terminals, and creating category sample labels. The example verification shows that the oil filled cable fault diagnosis method proposed in this paper can be adopted to effectively complete fault diagnosis, with an accuracy of 98.33% in the test set. Compared with traditional fault diagnosis models, the proposed method has good stability and high recognition accuracy, which can provide a theoretical basis for guaranteeing the reliable operation of high-voltage oil filled cable terminals. -
0. 引言
输电线路中的高压充油电缆终端对电能输送起着关键作用,且常以硅油作为绝缘填充剂。电缆充油终端用硅油易受到水分及电、机械和热等应力的综合作用使得其绝缘强度降低,从而使电缆终端成为电缆线路的绝缘薄弱环节[1-2]。充油电缆终端的运行过程中,其填充剂硅油会产生H2、CH4、C2H6、C2H2、C2H4、CO、CO2等气体[3-4]。这些气体的种类、含量大小以及不同气体间含量的比例关系将是判断高压充油电缆终端故障类型的关键。
当充油电缆终端内部温度过高或者存在局部/火花放电现象时,硅油会发生裂解,使得硅油中溶解气体的含量与种类迅速发生改变[5-6]。例如硅油内部发生高能放电现象时,H2和C2H2的含量会迅速增多,此时,二者的相关系数较大;硅油高温过热时,CH4和C2H4含量升高,二者的相关系数较大。油中溶解气体分析(dissolved gas analysis, DGA)准则可为充油电缆终端的故障诊断提供理论支撑[7-8],进而为保障电缆终端可靠运行提供一定理论基础与技术支撑。
目前,DGA法广泛用于评估油浸式电力设备中的故障[9],比如IEC三比值法[10]、Rogers比值法[11]、大卫三角形[12]等方法。不可否认,传统DGA方法在工程应用中发挥了重要作用,但这些方法由于采用线性分类,一定程度上会降低故障类型识别的准确性。另一方面,人工智能技术的快速发展,亦使油浸式电力设备的故障诊断方法趋于智能化。神经网络[13-14]、模糊理论算法[15-16]、支持向量机(support vector machine, SVM)[17]、分类回归树[18]等方法已应用于电力设备故障识别中。这些方法相较于传统方法有了较大进步,但仍存在一些不足之处。神经网络在一定程度上可以完成非线性映射,在故障分类时比线性函数更精确,但在处理大样本数据时收敛速度慢,且对新数据的泛化性能较弱。模糊理论算法利用粗糙的模型理论,能较好解决多分类边界样本划分问题,但在选择隶属度函数与划分输出空间方面缺少一定的客观性。SVM在小样本数据的训练上有突出优势,但对于大量DGA数据及多种故障分类的处理效率不高。以上方法普遍存在学习能力不足、处理效率较低、特征提取能力欠缺等问题。
随着大数据分析技术的发展及电力设备在线监测的普及,数据样本愈发庞大,IEC三比值法、Rogers比值法和大卫三角形法等传统DGA方法难以提高故障辨识的准确度等要求,极大影响了诊断的结果。同时,充油电缆终端故障诊断的特征量是判断故障诊断类型的重要部分,因此,正确提取充油电缆终端故障诊断的关键特征量,有助于提高充油电缆终端故障诊断模型的准确性。尽管经典方法对于输入特征没有明确规定,但最大互信息系数(maximal information coefficient, MIC)作为信息论中一种十分便捷的信息度量方法[19],能快速计算出变量之间的相关性。因此,本文采用最大互信息策略进行特征提取。
2006年由Hinton等人提出的优化深度置信网络(deep belief network, DBN) [20-21]在数据处理与特征优选方面有较大的优势,并且在处理辨识问题等方面表现优异。因此,本文以充油电缆终端故障诊断为研究对象,以硅油中溶解气体浓度分析为出发点,提出了基于MIC特征优选与DBN相结合的充油电缆终端故障诊断方法;为解决DBN网络参数选取困难的问题,采用改进阿基米德算法(improved Archimedes optimization algorithm, IAOA)求解超参数,进一步得到DBN网络模型的最佳参数;最后建立了基于MIC与IAOA-DBN的充油电缆终端故障诊断模型,有效提高了充油电缆终端故障诊断的识别精度,对进一步提高高压充油电缆终端的使用寿命和运行安全性提供了技术支撑。
1. 理论基础
1.1 最大互信息系数
互信息经常用来评估两个变量间的相关性,即在一个变量确定后,可知另一个变量的相关程度。互信息I(X; Y)的计算式如下:
$$ I(X;Y) = \int\limits_X {\int\limits_Y {P(X, Y)} } \lg \frac{{P(X, Y)}}{{P(X)P(Y)}} $$ (1) 式中:P(X, Y)表示参数X、Y的联合密度分布函数;P(X)与P(Y)分别为X、Y的边缘密度分布函数。
MIC是David N. Reshef等人提出的理论,用于衡量两个变量间的相互依存关系。MIC具有普适性和等价性,普适性是指在大多数情况下对多种函数关系都比较敏感,适用于线性、指数型等多种函数类型;等价性是指当加入相同噪声于不同函数关系类型中时,二者间的MIC值相近。本文采用MIC对充油电缆终端故障特征之间的相关性进行计算。
MIC方法不仅具备互信息的优势,而且改善了互信息的不足,优于传统互信息方法,它通过查找一种优异的离散化方式,将样本之间的互信息值转化为某种衡量模式,通过MIC指标判断相关性的强弱,其取值区间在[0, 1]。
MIC的值Mic的计算式为:
$$ {M}_{\text{ic}}(X;Y)=\underset{{n}_{X}{n}_{Y}<B\text{'}\text{'}}{\mathrm{max}}\frac{I(X;Y)}{{\mathrm{log}}_{2}\mathrm{min}({n}_{X}, {n}_{Y})} $$ (2) 式中:nX与nY分别为进行散点图网格划分时各坐标轴的单元格数量;B′′约为数据量的0.6次方。
1.2 深度置信网络
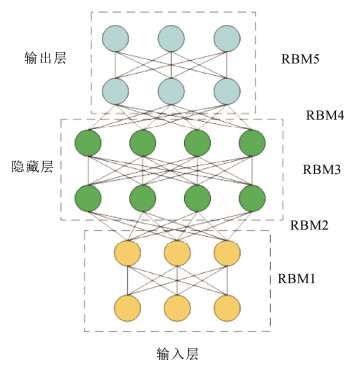
DBN是一种能够较好地完成特征识别、数据分类以及生成数据的模型,在机器学习领域得到广泛应用。DBN网络结构由受限玻耳兹曼机(restricted Boltzman machine, RBM)堆叠组成,包括输入层、隐藏层以及输出层。在DBN模型中,任意两个相邻层均可视为RBM结构,输入层中的神经元数与输入数据维数相同,用于从底层接收数据,并将计算结果输入到隐藏层。DBN网络模型如图 1所示。
DBN网络通过概率生成模型完成数据与类别之间的组合分布,逐层训练并优化网络,生成一个最大概率训练数据的网络结构,挖掘数据之间的相关性,实现分类和辨识的任务。同一层间的神经元彼此相互独立,使网络具有良好的独立性,使网络的计算能力得到改善,进一步提高了网络的训练速度。
DBN模型的训练过程可以概括为两个阶段:无监督学习CD阶段以及有监督学习BP阶段。在无监督训练过程中,前一个RBM的输出结果是下一个RBM的输入量,每个RBM都要经历正向计算和反向重构两个过程,经过不同批次的多次迭代,最终得到每个RBM的最优参数。在反向微调过程中,RBM提取原始数据特征,然后利用顶层分类器进行分类,最后通过BP算法结合类别信息对相关参数进行自上而下的微调,求出最优解。
1.3 阿基米德优化算法
AOA算法中,群体个体是浸没对象,在搜索过程中,随机初始化物体的体积、密度、加速度参数以及每个对象的位置[22-23]。在AOA迭代过程中,不断计算种群的适应度,直到满足迭代终止条件。在迭代过程中,个体不断调整自身密度、体积与加速度参数,让自身实现平衡。算法的详细流程如下所述。
初始化种群中所有个体的位置、体积、密度和加速度,具体计算式如式(3)—(5)所示。
$$ {O_i} = {l_{\text{b}}}_i + {r_{{\text{rand}}}}({u_{\text{b}}}_i - {l_{\text{b}}}_i), i = 1, 2, \cdots , N $$ (3) $$ \left\{ \begin{gathered} {d_{{\text{den}}}}_i = {r_{{\text{rand}}}} \hfill \\ {v_{{\text{vol}}}}_i = {r_{{\text{rand}}}} \hfill \\ \end{gathered} \right. $$ (4) $$ {a_{{\text{acc}}i}} = {l_{{\text{b}}i}} + {r_{{\text{rand}}}}({u_{{\text{b}}i}} - {l_{{\text{b}}i}}) $$ (5) 式中:Oi是第i个个体的位置;ubi、lbi分别为搜索范围的上、下边界;rrand是[0, 1]间的随机数,ddeni、vvoli和aacci分别为第i个个体的密度、体积和加速度。
个体i的适应度ffit可由式(6)计算,其值越小,个体越优。
$$ {f_{{\text{fit}}i}} = f({x_i}), i = 1, 2, \cdots , N $$ (6) 个体i的体积和密度更新式如式(7)所示。
$$ \{\begin{array}{l}{d}_{\text{den}i}^{\eta +1}={d}_{\text{den}i}^{\eta }+{r}_{\text{rand}}({d}_{\text{den}b}-{d}_{\text{den}i}^{\eta })\\ {v}_{\text{vol}i}^{\eta +1}={v}_{\text{vol}i}^{\eta }+{r}_{\text{rand}}({v}_{\text{vol}b}-{v}_{\text{vol}i}^{\eta })\end{array}\text{,}i=1, 2, \cdots , N $$ (7) 式中:η表示当前迭代次数;$ d_{{\text{den}}i}^\eta $、$ d_{{\text{den}}i}^{\eta + 1} $是第η与η+1代第i个个体的密度;$ v_{{\text{vol}}i}^\eta $、$ v_{{\text{vol}}i}^{\eta + 1} $是第η与η+1代第i个个体的体积。
若液体中的物体发生碰撞,则AOA为局部搜索阶段,若未发生碰撞,则AOA为全局搜索阶段,设置转移因子(transfer factor, TF)范围在(0, 1]之间,计算式如下:
$$ {T_{{\text{tf}}}} = {\text{exp}}(\frac{{\eta - {\eta _{\max }}}}{{{\eta _{\max }}}}) $$ (8) 式中:$ {\eta _{\max }} $表示最大迭代次数。
若Ttf≤0.5,则加速度更新计算式如下:
$$ a_{{\text{acc}}i}^{\eta + 1} = \frac{{{d_{{\text{den}}c}} + {v_{{\text{vol}}c}}{a_{{\text{acc}}c}}}}{{d_{{\text{den}}i}^{\eta + 1}v_{{\text{vol}}i}^{\eta + 1}}} $$ (9) 式中:下标c为种群选的随机碰撞物体;ddenc代表随机碰撞物体的密度;vvolc代表随机碰撞物的体积;aaccc代表随机碰撞物体的加速度;$ a_{{\text{acc}}i}^{\eta + 1} $是η+1代第i个个体的加速度。
若Ttf > 0.5,则物体间无碰撞,由式(10)更新加速度。
$$ a_{{\text{acc}}i}^{\eta + 1} = \frac{{{d_{{\text{den}}b}} + {v_{{\text{vol}}b}} \cdot {a_{{\text{acc}}b}}}}{{d_{{\text{den}}i}^{\eta + 1} + v_{{\text{vol}}i}^{\eta + 1}}} $$ (10) 采用式(11)对加速度进行归一化处理。
$$ a_{{\text{acc}}i - s}^{\eta + 1} = u'\frac{{a_{{\text{acc}}i}^{\eta + 1} - \min ({a_{{\text{acc}}}})}}{{\max ({a_{{\text{acc}}}}) - \min ({a_{{\text{acc}}}})}} + l' $$ (11) 式中:$ a_{{\text{acc}}i - s}^{\eta + 1} $是η+1代第i个个体归一化的加速度;min(aacc)、max(aacc)分别代表加速度矩阵中最小值和最大值;u′和l′分别调整归一化范围。
若Ttf≤0.5,则属于勘探阶段,各物体更新位置计算式如式(12)所示。
$$ {\mathbf{x}}_i^{\eta + 1} = {\mathbf{x}}_i^\eta + C{\prime _1}{r_{{\text{rand}}}}a_{{\text{acc}}i - s}^{\eta + 1}d({{\mathbf{x}}_{{\text{rand}}}} - {\mathbf{x}}_i^\eta ) $$ (12) 式中:$ {\mathbf{x}}_i^\eta $和$ {\mathbf{x}}_i^{\eta + 1} $分别为第i个个体在第η、η+1次迭代的位置向量;C′1是常数,本文取2;xrand表示第i个随机个体在第η次迭代的位置向量;d是密度因子。
若Ttf > 0.5,则属于局部探索阶段,各物体按式(13)进行位置更新。
$$ {\mathbf{x}}_i^{\eta + 1} = {\mathbf{x}}_{{\text{best}}}^\eta + F{C'_2}{r_{{\text{rand}}}}a_{{\text{acc}}i - s}^{\eta + 1}d(T{{\mathbf{x}}_{{\text{best}}}} - {\mathbf{x}}_i^\eta ) $$ (13) 式中:$ {C'_2} $为常数,本文取6;$ {x_{{\text{best}}}} $为全局最优个体;T定义为T=$ {C'_3} $Ttf,$ {C'_3} $为常数,本文取2;F代表改变运动方向的标志,其定义如式(14)所示:
$$ F = \left\{ \begin{gathered} + 1, P \leqslant 0.5 \hfill \\ - 1, P > 0.5 \hfill \\ \end{gathered} \right. $$ (14) 式中:P=2rrand−$ {C'_4} $,$ {C'_4} $为常数,本文取2。
密度递减因子计算式如下所示:
$$ {d^{\eta + 1}} = \exp (\frac{{{\eta _{\max }} - \eta }}{{{\eta _{\max }}}}) - (\frac{\eta }{{{\eta _{\max }}}}) $$ (15) 1.4 多策略改进阿基米德优化算法
为进一步扩大算法的搜索空间,本文采用混沌理论对种群进行初始化多样性处理,从而改善算法的优化性能。优化原理可概括为:采用映射原理构造混沌序列,再转化到寻优变量空间中。因为cos混沌模型是一种多重映射折叠的混沌模型,具有尺度多样性和随机性的特点,所以本文首先采用cos混沌处理初始种群,然后建立反向种群;最后,对比分析反向种群与cos混沌种群二者的适应度指标,择优选择初始种群,从而有助于寻找到最优解。cos混沌映射计算式如式(16)所示。
$$ \begin{cases}X_{n+1}^{\prime}=\cos \left(\frac{2}{X_n^{\prime}}\right), n=0,1, \cdots, N \\ -1 \leq X_n^{\prime} \leq 1, \quad X_n^{\prime} \neq 0\end{cases} $$ (16) 式中:Xn′在(–1, 1)之间,初值不为0,将cos混沌序列映射到解空间,得到cos混沌种群,种群个体可由式(17) 计算。
$$ {X'_{i + 1, j}} = \cos (\frac{2}{{{{X'}_{i, j}}}}) $$ (17) 式中,$ {X'_{i + 1, j}} $为第i+1个cos混沌种群的第j维数值。
由cos混沌种群计算反向种群,反向种群个体可由式(17)计算。
$$ X_{ij}^* = {x'_{\min j}} + {x'_{\max j}} - {X'_{ij}} $$ (18) 式中:$ [{x'_{\min j}}, {x'_{\max j}}] $为搜索范围边界。
标准AOA算法是依靠种群中随机个体计算种群位置,缺少先验条件,并且不能保证随机个体是更优的解,导致算法的整体优化性能较差。为改善标准AOA算法的寻优性能,本文引入算数交叉算子思想,对应算式见式(19)。
$$ X_{{\text{new}}}^{\eta + 1} = \chi X_i^{\eta + 1} + (1 - \chi )({X_{{\text{best}}}} - X_i^{\eta + 1}) $$ (19) 式中:$ \chi $为(0, 1)的随机数。
采用算数交叉算子策略后,可以加快群体向全局最优范围靠近的速度,在一定程度上,有助于丰富种群多样性。将全局最佳个体与当前个体交叉处理,有助于提高算法的全局寻优能力,但不能保证新个体优于原始个体。因此,采用以下策略不断更新最优解,计算式如式(20)所示。
$$ X_i^{\eta + 1} = \left\{ \begin{gathered} X_w^{\eta + 1}, f(X_i^{\eta + 1}) \geqslant f(X_w^{\eta + 1}) \hfill \\ X_i^{\eta + 1}, f(X_i^{\eta + 1}) \lt f(X_w^{\eta + 1}) \hfill \\ \end{gathered} \right. $$ (20) 标准AOA算法中的密度递减因子策略对算法的全局寻优搜索能力有一定的限制,因此本文参考余弦函数思想理论,在求解中引入余弦函数,其求解式如式(21)所示。
$$ {d^{\eta + 1}} = {d_1} - ({d_1} - {d_2})\cos (\frac{{\text{π }}}{{{\omega _{\text{d}}}}}{(\frac{\eta }{{{\eta _{\max }}}})^2}) $$ (21) 式中:ωd为控制曲线平滑系数;d1指迭代初时密度递减因子初始值;d2指迭代末时密度递减因子终止值。
1.5 算法性能测试
采用基准测试函数可以合理评判算法的有效性,为了评价IAOA算法的有效性,选取以下测试函数对IAOA算法进行性能测试。测试函数如下:
1)Sphere函数,表达式为:
$$ {F_{01}}(x) = \sum\limits_{i = 1}^n {x_i^2} $$ (22) 设置维度30,范围区间在[–100, 100],函数最小值为0。
2)Schwefel2.22函数,表达式为:
$$ {F_{02}}(x) = \sum\limits_{i = 1}^n {\left| {{x_i}} \right|} + \prod\limits_{i = 1}^n {\left| {{x_i}} \right|} $$ (23) 设置维度30,范围区间在[–10, 10],函数最小值为0。
3)Schwefel1.2函数,表达式为:
$$ {F_{03}}(x) = {\sum\limits_{i = 1}^n {\left( {\sum\limits_{j = 1}^i {{x_j}} } \right)} ^2} $$ (24) 设置维度30,范围区间在[–100, 100],函数最小值为0。
4)Schwefel2.21函数,表达式为:
$$ {F_{04}}(x) = ma{x_i}\{ \left| {{x_i}} \right|, 1 \leqslant i \leqslant D\} $$ (25) 设置维度30,范围区间在[–100, 100],函数最小值为0。
5)Ackley函数,表达式为:
$$ {F_{05}}(x) = - 20\text{exp}( - 0.2\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {x_i^2} } - \exp (\frac{1}{n}\sum\limits_{i = 1}^n {\cos 2{\text{π }}{x_i}} )){\text{ + 20 + e}} $$ (26) 设置维度30,范围区间在[–20, 20],函数最小值为0。
6)Rastrigin函数,表达式为:
$$ {F_{06}}(x) = \sum\limits_{i = 1}^n {\left( {x_i^2 - 10\cos (2{\text{π }}{x_i}) + 10} \right)} $$ (27) 设置维度30,范围区间在[–5, 5],函数最小值为0。
为了验证本文所提的IAOA算法寻优性能,本文对IAOA进行了性能测试,将AOA算法与IAOA算法的种群规模均设置为30,迭代次数设置为1000,将F01–F06基准测试函数连续独立运行20次,得到两者算法的均值、标准差、最差值与最优值作为衡量标准来验证算法性能。标准差越大,说明算法鲁棒性能越弱,最差值和最优值分别代表最差、最佳适应度值。算法的收敛结果如表 1所示。
表 1 函数寻优结果比较表Table 1. Function optimization result comparison测试函数 方法 最优值 最差值 平均值 标准差 F01 AOA 1.13×10–6 2.90×10–4 4.99×10–5 7.728×10–5 IAOA 2.74×10–7 6.66×10–5 4.28×10–6 1.527×10–7 F02 AOA 6.77×10–4 7.83×10–3 2.65×10–3 1.62×10–3 IAOA 6.58×10–4 4.49×10–3 2.49×10–3 1.001×10–3 F03 AOA 5.783 110.361 42.926 28.176 IAOA 5.89 2.18 13.57 4.920 F04 AOA 1.391 5.302 2.451 1.056 IAOA 1.086 4.553 2.72 1.013 F05 AOA 0.000 17 1.157 0.060 0 0.258 IAOA 0.000 088 0.888 0.008 8 0.202 F06 AOA 14.596 32.327 21.957 5.034 IAOA 0 0 0 0 由表 1知,对比分析各测试函数的评价指标,IAOA法求解结果中标准差和平均值相对最小,说明IAOA算法在求解精度与稳定性方面要高于AOA算法,尤其是对于测试函数F06而言,其指标已经达到了理论最优值。
2. 基于MIC与IAOA-DBN电缆终端故障诊断模型
2.1 特征优选
当充油电缆终端处于不同电、热环境而产生不同故障时,硅油产生的特征气体的主次以及含量也不同。因此,为能够较全面找到优选特征量,初步采用的特征气体比值有以下9种:CH4/H2、C2H4/C2H2、C2H4/C2H6、C2H2/(C1+C2)、H2/(H2+C1+C2)、C2H4/(C1+C2)、CH4/(C1+C2)、C2H6/(C1+C2)与(CH4+C2H4)/(C1+C2)。其中,C1=CH4+C2H6,C2=C2H4+C2H2,若使用所有特征气体比值作为特征输入,则会由于特征维数过多而使诊断模型的结构复杂,因此,本文采用MIC对气体的特征比值进行约简,上述9种特征量与故障类型之间的MIC值如表 2所示。
表 2 MIC系数值Table 2. MIC coefficient value特征序号 特征量 MIC 1 CH4/H2 0.487 2 2 C2H4/C2H2 0.638 6 3 C2H4/(C1+C2) 0.342 3 4 CH4/(C1+C2) 0.281 2 5 C2H4/C2H6 0.482 3 6 C2H2/(C1+C2) 0.672 9 7 H2/(H2+C1+C2) 0.505 3 8 C2H6/(C1+C2) 0.434 9 9 (CH4+C2H4)/(C1+C2) 0.335 8 以MIC指标0.45为参考,筛选后的输入特征量可选用下述6种:CH4/H2、C2H4/C2H2、C2H4/C2H6、C2H2/(C1+C2)、H2/(H2+C1+C2)。
2.2 IAOA-DBN故障诊断模型
将优选特征量作为DBN诊断模型的输入,并规范化处理。采用表 3所示one-hot编码方式,将充油电缆终端故障类型以编码方式按列向量排序,构造类别特征矩阵。
表 3 充油式电缆终端故障类型编码Table 3. Fault type code for oil filled cable terminals编号 故障类型 编码 1 低能放电 100 000 2 高能放电 010 000 3 中低温过热 001 000 4 高温过热 000 100 5 正常 000 010 6 局部放电 000 001 2.3 IAOA-DBN故障诊断流程
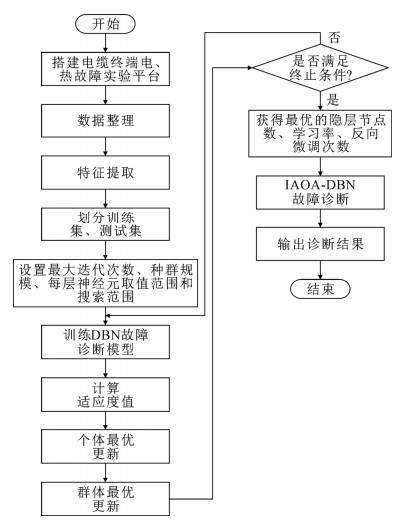
通过IAOA算法对DBN网络的隐层节点数、学习率因子以及反向微调次数等参数进行寻优,IAOA-DBN充油电缆终端故障诊断流程见图 2。详细步骤如下:
第1步:搭建充油电缆终端电、热故障实验平台,获得多组故障数据集对应的气体组分及含量。
第2步:确定输入IAOA-DBN充油电缆终端故障诊断模型的输入样本特征量,对输出故障类型编码。
第3步:将输入特征量归一化处理,并划分训练集与测试集数据样本。
第4步:设置IAOA算法相关参数、DBN网络每层神经元的取值范围以及搜索范围。
第5步:训练DBN网络,将DBN网络诊断的错误率作为优化的目标函数值。
第6步:根据适应度值确定搜索方向,比较个体与群体最优解,提升模型正确率。
第7步:若满足迭代终止条件,则得到DBN模型最佳参数值,否则返回第5步。
第8步:根据IAOA优化获得的最佳参数指标建立DBN网络模型。
第9步:将测试集样本输入到训练好的网络中,输出模型诊断结果。
优化后网络模型的最佳参数设置如表 4所示。
表 4 参数设置及含义Table 4. Parameter setting and meaning参数名 参数含义 最佳参数值 numepochs 反向微调次数 100 batchsize 批尺寸 10 momentum 动量 0 alpha 学习率因子 0.1 dbn.size1 第1层神经元个数 19 dbn.size2 第2层神经元个数 19 dbn.size3 第3层神经元个数 19 3. 实验与算例分析
分别搭建了充油电缆终端过热及放电故障实验平台,通过气相色谱分析得到充油电缆终端不同故障类型下硅油中溶解气体浓度的特征气体含量,进而验证MIC与IAOA-DBN充油电缆终端故障诊断模型的有效性。
3.1 充油电缆终端内部硅油过热实验平台
首先,选用PMX- 200型运动黏度为100 mm2/s的硅油为原材料,将油杯置于电-热老化实验箱中,依据《电缆终端绝缘油中溶解气体分析导则(报批稿)》设定正常情况(无故障)、中低温过热故障(120 ℃)、高温过热故障(180 ℃)进行过热老化实验。
其次,圆柱形油杯为石英材质,直径为15 cm,高度为30 cm;黄铜针-板电极的板电极直径为5 cm,厚度为0.5 cm;针电极尖部夹角为30°。实验箱为WBL- 230NB型干燥箱改造而成,其控温范围为室温至300 ℃,温度误差为±1 ℃。每一情况下的详细实验步骤如下:
取适量硅油(800 mL)样品进行脱气及干燥处理;取2组适量硅油(200 mL)分别于容积为800 mL的油杯内,将其放于高温老化箱中进行热老化实验;分别设置老化箱的温度和外加电压,进行加速热老化实验;设置热老化时间每隔24 h取样一次,分别取两组不同老化温度下的硅油样品。
最后,对老化后的油样进行气相色谱分析。实验中,对硅油中溶解气体含量每个试样均测试2次,取其平均值,若几次平行测试结果分散性较大,则对该项数据重新测试,以获得多组可靠的中低温过热、高温过热条件下的硅油中溶解特征气体的含量。所用设备及型号为:
ZKPZD-5A多功能脱气振荡仪,50 ℃下以恒温定时振荡器方式(控温精确度±0.3 ℃;往复振荡频率(275±3)次/min,振幅(35±3) mm,振荡20 min后静止10 min)进行脱气;采用GC-2020型气相色谱仪(双柱分流系统,氢火焰检测器、氧化锆检测器、镍触媒转化器,GDX-502色谱分析柱和5A分子筛)进行气相色谱分析。
3.2 充油电缆终端放电实验平台
依据《电缆终端绝缘油中溶解气体分析导则(报批稿)》设定正常情况(无故障)、低能放电故障(间歇性火花放电)、高能放电故障(连续火花放电)及局部放电进行电老化实验。实验中采用针-板电极(设置间距0.5 cm)来模拟极不均匀电场,选用恒稳直流电压(HY-DC300型直流试验装置)对充油电缆终端用硅油进行低能放电、局部放电以及高能放电实验。
实验中,采用1.0 kV/s的升压速率,缓慢加压至硅油中发生间歇性击穿(试样中产生火花放电)时停止升压(对应电压约为25 kV),连续2次击穿间隔约为3~5 s。利用HYJF-2013型局部放电测量仪采集局部放电信号,待放电10次时停止加压,老化实验结束。
对不同放电环境的油样进行气相色谱分析,得到多组低能放电故障、高能放电故障以及局部放电故障下的硅油中溶解特征气体含量。
3.3 对比结果分析
本文所用数据为2021–03–01—2021–08–31期间184 d共368组硅油的气相色谱数据,监测周期为12 h。本文从测量得到的多组充油电缆终端故障样本数据中随机选取300个样本,每种故障类型平均选取250个样本,再从每种类别中随机选取80%的样本作为训练集,剩余20%的样本作为测试集。采用IAOA-DBN方法诊断充油电缆终端的故障,并将诊断结果与DBN、广义回归神经网络(general regression neural network, GRNN)、SVM 3种常规的分类方法进行对比分析。部分充油电缆终端故障数据与故障类型如表 5所示。不同充油电缆终端故障诊断模型的结果如表 6所示。
表 5 部分充油电缆终端故障类型样本数据Table 5. Sample data of partial oil filled cable terminal fault types体积分数/10–6 故障类型 H2 CH4 C2H6 C2H4 C2H2 102.72 33.82 7.74 19.60 4.86 低能放电 312.21 48.71 15.19 118.97 132.06 高能放电 6.32 194.21 118.56 127.45 2.12 中低温过热 82.31 119.20 32.20 234.21 3.45 高温过热 3.21 1.25 0.54 0.65 0.78 正常 652.10 50.21 34.23 21.01 21.36 局部放电 表 6 各种充油电缆终端故障诊断方法的实验结果Table 6. Experimental results of various fault diagnosis methods for oil-filled cable terminals算法 训练集准确率/% 测试集准确率/% SVM 76.25 73.33 GRNN 72.92 70.00 DBN 83.75 81.67 AOA-DBN 90.83 91.67 IAOA-DBN 99.58 98.33 从表 6的测试集结果可以看出SVM模型的诊断准确率为73.33%,GRNN模型的诊断准确率为70%,DBN模型的诊断准确率优于SVM和GRNN模型,其准确率达到了81.67%,AOA-DBN模型的诊断准确率为91.67%,而本文所提出的IAOA-DBN模型的诊准确率为98.33%,明显优于传统方法,可以满足工程中实际需求。
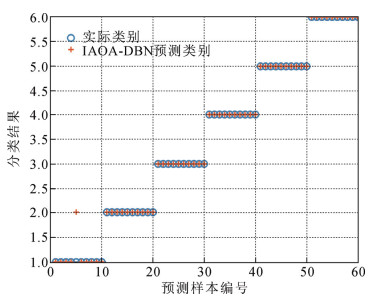
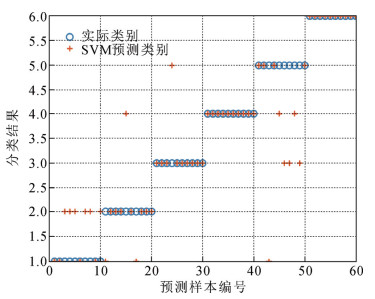
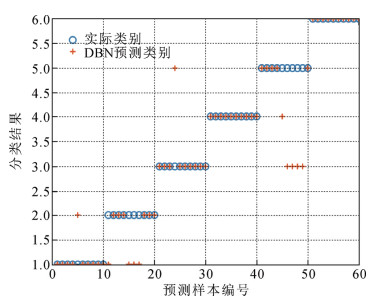
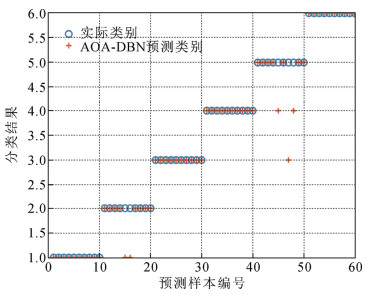
本文对测试集的故障诊断结果进行详细分析,图 3是IAOA-DBN充油电缆终端测试集样本故障诊断结果与真实结果的对比分析图。其中纵坐标1、2、3、4、5及其6分别代表低能放电故障、高能放电故障、中低温过热故障、高温过热故障、正常情况及局部放电故障的6种故障类型,蓝色圆圈表示充油电缆终端样本的真实故障类别,红色加号表示充油电缆终端样本的模型诊断类别,二者重合则表示模型诊断正确,反之,模型诊断错误。
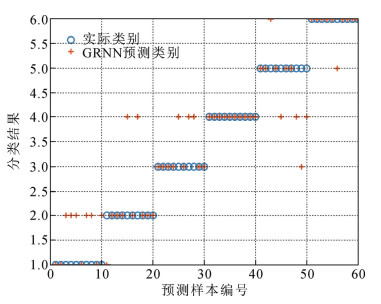
图 4为GRNN模型的故障诊断结果。由图 4可以看出GRNN模型除了对充油电缆终端高温过热故障全部诊断正确外,其余5种类别故障均存在一定程度的诊断错误率,尤其是将低能放电故障诊断为高能放电故障。图 5中展示了SVM充油电缆终端故障诊断的结果,SVM故障诊断结果中高温过热故障和局部放电故障均诊断正确,其余4种类别故障也存在一定程度的错误率,还是将低能放电故障误判为高能放电故障的数量较多。图 6中展示了DBN充油电缆终端故障诊断模型的诊断结果,相比于SVM模型和GRNN模型,该模型表现出了较好的诊断结果,但依然存在个别样本的正常状态诊断成了中低温过热和高温过热故障。图 7为AOA-DBN充油电缆终端故障诊断模型,其准确率相对于上述3种方法均有一定的提升。而本文提出的IAOA- DBN充油电缆终端故障诊断模型的结果,仅有个别低能放电故障误判为高能放电故障,明显优于上述几种充油电缆终端故障诊断模型的结果。
基于上述对比结果分析,本文所提出的MIC与IAOA-DBN充油电缆终端故障诊断模型表现出优良的故障诊断正确率,在有限充油电缆终端故障样本的情况下,能够根据气相色谱分析得到的硅油中溶解特征气体数据样本,实现准确可靠的充油电缆终端故障诊断。
4. 结论
1)传统的方法进行充油电缆终端故障诊断时,准确率较低,不能满足实时性等要求,使用MIC理论来提取特征量,可以提高充油电缆终端故障诊断模型的性能,以保证模型的可靠性与诊断结果的准确性。
2)针对AOA算法搜索能力存在的不足,采用多策略改进AOA算法方法,有助于提高AOA算法
全局搜索和局部开发能力,有效解决DBN模型参数选取困难的问题,进一步提高了充油电缆终端故障诊断的准确率。
3)通过模拟搭建充油电缆终端电、热故障实验平台,收集了真实的充油电缆终端多重故障数据样本,为基于MIC与IAOA-DBN的充油电缆终端故障诊断模型提供了数据支撑,并且利用测试样本数据将本文方法的诊断结果与传统方法进行对比分析,验证了诊断模型的可靠性。
此外,本文所提出的方法不仅适用于处理多重故障状态下高压充油电缆终端的故障辨识问题,而且在一定程度上对充油电缆终端的寿命评估提供了一定的参考价值,有利于保障电缆终端的安全运行,提供安全可靠的供电环境。
-
表 1 函数寻优结果比较表
Table 1 Function optimization result comparison
测试函数 方法 最优值 最差值 平均值 标准差 F01 AOA 1.13×10–6 2.90×10–4 4.99×10–5 7.728×10–5 IAOA 2.74×10–7 6.66×10–5 4.28×10–6 1.527×10–7 F02 AOA 6.77×10–4 7.83×10–3 2.65×10–3 1.62×10–3 IAOA 6.58×10–4 4.49×10–3 2.49×10–3 1.001×10–3 F03 AOA 5.783 110.361 42.926 28.176 IAOA 5.89 2.18 13.57 4.920 F04 AOA 1.391 5.302 2.451 1.056 IAOA 1.086 4.553 2.72 1.013 F05 AOA 0.000 17 1.157 0.060 0 0.258 IAOA 0.000 088 0.888 0.008 8 0.202 F06 AOA 14.596 32.327 21.957 5.034 IAOA 0 0 0 0 表 2 MIC系数值
Table 2 MIC coefficient value
特征序号 特征量 MIC 1 CH4/H2 0.487 2 2 C2H4/C2H2 0.638 6 3 C2H4/(C1+C2) 0.342 3 4 CH4/(C1+C2) 0.281 2 5 C2H4/C2H6 0.482 3 6 C2H2/(C1+C2) 0.672 9 7 H2/(H2+C1+C2) 0.505 3 8 C2H6/(C1+C2) 0.434 9 9 (CH4+C2H4)/(C1+C2) 0.335 8 表 3 充油式电缆终端故障类型编码
Table 3 Fault type code for oil filled cable terminals
编号 故障类型 编码 1 低能放电 100 000 2 高能放电 010 000 3 中低温过热 001 000 4 高温过热 000 100 5 正常 000 010 6 局部放电 000 001 表 4 参数设置及含义
Table 4 Parameter setting and meaning
参数名 参数含义 最佳参数值 numepochs 反向微调次数 100 batchsize 批尺寸 10 momentum 动量 0 alpha 学习率因子 0.1 dbn.size1 第1层神经元个数 19 dbn.size2 第2层神经元个数 19 dbn.size3 第3层神经元个数 19 表 5 部分充油电缆终端故障类型样本数据
Table 5 Sample data of partial oil filled cable terminal fault types
体积分数/10–6 故障类型 H2 CH4 C2H6 C2H4 C2H2 102.72 33.82 7.74 19.60 4.86 低能放电 312.21 48.71 15.19 118.97 132.06 高能放电 6.32 194.21 118.56 127.45 2.12 中低温过热 82.31 119.20 32.20 234.21 3.45 高温过热 3.21 1.25 0.54 0.65 0.78 正常 652.10 50.21 34.23 21.01 21.36 局部放电 表 6 各种充油电缆终端故障诊断方法的实验结果
Table 6 Experimental results of various fault diagnosis methods for oil-filled cable terminals
算法 训练集准确率/% 测试集准确率/% SVM 76.25 73.33 GRNN 72.92 70.00 DBN 83.75 81.67 AOA-DBN 90.83 91.67 IAOA-DBN 99.58 98.33 -
[1] 郭蕾, 曹伟东, 白龙雷, 等. 热氧老化EPR电缆绝缘局部放电特性及劣化机理[J]. 高电压技术, 2021, 47(1): 231-240. DOI: 10.13336/j.1003-6520.hve.20191353 GUO Lei, CAO Weidong, BAI Longlei, et al. Partial discharge characteristics and degradation mechanism of EPR cable insulation by thermo-oxygen aging[J]. High Voltage Engineering, 2021, 47(1): 231-240. DOI: 10.13336/j.1003-6520.hve.20191353
[2] 王若丞, 贺云逸, 康洪玮, 等. 电缆接头绝缘用硅橡胶热老化及超声特性[J]. 高电压技术, 2021, 47(9): 3181-3188. DOI: 10.13336/j.1003-6520.hve.20201160 WANG Ruocheng, HE Yunyi, KANG Hongwei, et al. Thermal aging and ultrasonic characteristics of silicone rubber for cable joint insulation[J]. High Voltage Engineering, 2021, 47(9): 3181-3188. DOI: 10.13336/j.1003-6520.hve.20201160
[3] 付朝霞. 220 kV电缆终端硅油老化鉴定试验与分析[J]. 电力安全技术, 2013, 15(7): 27-29. FU Zhaoxia. Aging identification test and analysis of silicone oil in 220 kV cable terminal[J]. Electric Safety Technology, 2013, 15(7): 27-29.
[4] 李光茂, 乔胜亚, 朱晨, 等. 变压器油中溶解甲醇拉曼光谱检测定量分析方法[J]. 高电压技术, 2021, 47(6): 2007-2014. DOI: 10.13336/j.1003-6520.hve.20200820 LI Guangmao, QIAO Shengya, ZHU Chen, et al. Quantitative analysis method for Raman spectral detection of methanol dissolved in transformer oil[J]. High Voltage Engineering, 2021, 47(6): 2007-2014. DOI: 10.13336/j.1003-6520.hve.20200820
[5] 刘展程, 王爽, 唐波. 基于SSA-BiGRU-Attention模型的变压器油中溶解气体含量预测[J]. 高电压技术, 2022, 48(8): 2972-2981. DOI: 10.13336/j.1003-6520.hve.20220099 LIU Zhancheng, WANG Shuang, TANG Bo. Prediction of dissolved gas content in transformer oil based on SSA-BiGRU-Attention model[J]. High Voltage Engineering, 2022, 48(8): 2972-2981. DOI: 10.13336/j.1003-6520.hve.20220099
[6] 朱庆东, 朱文兵, 王浩哲, 等. 基于油中溶解气监测的变压器在线半监督故障诊断方法研究[J]. 电网技术, 2023, 47(3): 1031-1037. ZHU Qingdong, ZHU Wenbin, WANG Haozhe, et al. Online semi-supervised fault diagnosis of transformer based on dissolved gas in oil[J]. Power System Technology, 2023, 47(3): 1031-1037.
[7] 王健一, 李金忠, 凌愍, 等. 新版电力行业标准《变压器油中溶解气体分析判断导则》解读[J]. 变压器, 2014, 51(12): 49-53. WANG Jianyi, LI Jinzhong, LING Min, et al. Interpretation of the new electricity industry standard guide to the analysis and the diagnosis of gases dissolved in transformer oil[J]. Transformer, 2014, 51(12): 49-53.
[8] 张鹏, 齐波, 刘娟, 等. 电力变压器油中溶解气体数据的分布特征参数快速计算方法[J]. 中国电机工程学报, 2022, 42(5): 2001-2011. ZHANG Peng, QI Bo, LIU Juan, et al. Fast calculation method for distribution characteristic parameters of dissolved gas data in power transformer oil[J]. Proceedings of the CSEE, 2022, 42(5): 2001-2011.
[9] XIANG C M, HUANG Z Y, LI J, et al. Graphic approaches for faults diagnosis for camellia insulating liquid filled transformers based on dissolved gas analysis[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(5): 1897-1903. DOI: 10.1109/TDEI.2018.007247
[10] 张卫华, 苑津莎, 王杉, 等. 基于改良三比值法的变压器故障基本信度分配计算方法[J]. 电力系统保护与控制, 2015, 43(7): 115-121. ZHANG Weihua, YUAN Jinsha, WANG Shan, et al. A calculation method for transformer fault basic probability assignment based on improved three-ratio method[J]. Power System Protection and Control, 2015, 43(7): 115-121.
[11] KHANNA A, BISHT P. Rogers ratio test for fault diagnosis of transformer using dissolved gas analysis[J]. Materials Today: Proceedings, 2022, 71: 243-246. DOI: 10.1016/j.matpr.2022.08.519
[12] SONI R, MEHTA B. Graphical examination of dissolved gas analysis by ratio methods and Duval triangle method to investigate internal faults of power transformer[J]. Materials Today: Proceedings, 2022, 62: 7098-7103. DOI: 10.1016/j.matpr.2022.02.029
[13] PATEKAR K D, CHAUDHRY B. DGA analysis of transformer using artificial neutral network to improve reliability in power transformers[C]//2019 IEEE 4th International Conference on Condition Assessment Techniques in Electrical Systems (CATCON). Chennai, India: IEEE, 2019: 1-5.
[14] ZAN T, WANG H, WAMG M, et al. Application of multi-dimension input convolutional neural network in fault diagnosis of rolling bearings[J]. Applied Sciences, 2019, 9(13): 2690. DOI: 10.3390/app9132690
[15] XU A R, GU C L, LIU B L, et al. Research on fault diagnosis of microgrid based on variational sparse Bayesian fuzzy H-network[J]. International Journal of Low-Carbon Technologies, 2022, 17: 1-10. DOI: 10.1093/ijlct/ctab071
[16] 周健, 黄昕, 邹剑, 等. 变压器油中溶解气体故障诊断的改进模糊算法[J]. 广东电力, 2015, 28(3): 86-91. ZHOU Jian, HUANG Xin, ZOU Jian, et al. Improved fuzzy algorithm for fault diagnosis on dissolved gas in transformer oil[J]. Guangdong Electric Power, 2015, 28(3): 86-91.
[17] BENMAHAMED Y, KHERIF O, TEGUAR M, et al. Accuracy improvement of transformer faults diagnostic based on DGA data using SVM-BA classifier[J]. Energies, 2021, 14(10): 2970. DOI: 10.3390/en14102970
[18] 黄新波, 李文君子, 宋桐, 等. 采用遗传算法优化装袋分类回归树组合算法的变压器故障诊断[J]. 高电压技术, 2016, 42(5): 1617-1623. DOI: 10.13336/j.1003-6520.hve.20160412052 HUANG Xinbo, LI Wenjunzi, SONG Tong, et al. Application of Bagging-CART algorithm optimized by genetic algorithm in transformer fault diagnosis[J]. High Voltage Engineering, 2016, 42(5): 1617-1623. DOI: 10.13336/j.1003-6520.hve.20160412052
[19] 张俐, 袁玉宇, 王枞. 基于最大相关信息系数的FCBF特征选择算法[J]. 北京邮电大学学报, 2018, 41(4): 86-90. ZHANG Li, YUAN Yuyu, WANG Cong. FCBF feature selection algorithm based on maximum information coefficient[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(4): 86-90.
[20] CHEN C, SHI J T, SHEN M Q, et al. Pseudo-label guided sparse deep belief network learning method for fault diagnosis of radar critical components[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 3510212.
[21] 李锦键, 王兴贵, 杨维满, 等. 基于改进递归深度信念网络的CSP电站短期出力预测[J]. 太阳能学报, 2022, 43(7): 225-232. LI Jinjian, WANG Xinggui, YANG Weiman, et al. CSP station output power short-term forecast based on improved RNN-DBN[J]. Acta Energiae Solaris Sinica, 2022, 43(7): 225-232.
[22] 罗仕杭, 何庆. 融合Sin混沌和分段权值的阿基米德优化算法[J]. 计算机工程与应用, 2022, 58(14): 63-72. LUO Shihang, HE Qing. Archimedes optimization algorithm combining Sin chaos and segmented weights[J]. Computer Engineering and Applications, 2022, 58(14): 63-72.
[23] HASHIM F A, HUSSAIN K, HOUSSEIN E H, et al. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems[J]. Applied Intelligence, 2021, 51(3): 1531-1551.
-
期刊类型引用(0)
其他类型引用(1)




 下载:
下载:
 下载:
下载:



