Experiment of Self-healing Properties of Metallized Films Under Multiple Physical Fields
-
摘要: 金属化膜电容器是柔性直流输电系统换流阀的核心元件，掌握电容器用金属化膜在复杂工作环境下的自愈参数，对高性能电容器的研制、提高能源输送效率具有关键性作用。该文基于金属化膜电容器实际运行工况，利用搭建的多物理场自愈测试平台，开展了金属化膜在电-热-力复合作用下的自愈特性测试，得出电压、温度、压强对金属化膜自愈的交互影响，随着温度的上升，电压对自愈特性的影响愈发明显，而随着压强的上升，电压对自愈特性的影响逐渐减弱，当压强达到4 MPa以上时，电压对自愈特性影响非常小。通过对自愈特征量的统计，建立自愈参数间的关联关系，分析得到自愈面积和自愈数量呈负相关性，当有效区内自愈数量从1个/cm2增加到30个/cm2时，平均单个自愈点面积从16 mm2缩小为1 mm2；自愈电流峰值、自愈时间与自愈电压呈正相关性，当电压达到3.5 kV时，自愈时间可达4 μs，自愈电流峰值可达5 A；而自愈能量与自愈电压呈出幂指数为2.316的幂值函数关系；同时，根据自愈参数间的关联关系，提出了一种对自愈能量的快速估算方法。该研究涉及金属化膜材料性能的关键特征参数和判据集合，对金属化膜电容器的优化设计提供数据支撑。Abstract: Metallized film capacitors are core components of the converter valves in flexible high-voltage direct-current (HVDC) transmission systems. Mastering the self-healing parameters of metallized films under complex operating conditions is crucial for the development of high-performance capacitors and improving energy transmission efficiency. Based on the actual operating conditions of metallized film capacitors, this paper utilizes a multi-physical field self-healing testing platform to conduct self-healing characteristic tests under the combined effects of electrical, thermal, and mechanical stresses. The study reveals the interactive effects of voltage, temperature, and pressure on the self-healing behavior of metallized films. It is found that as the temperature increases, the impact of voltage on self-healing becomes more remarkable; while as the pressure rises, the impact of voltage on self-healing gradually diminishes. When the pressure exceeds 4 MPa, the effect of voltage on self-healing becomes negligible. Through statistical analysis of self-healing characteristics, this paper establishes a correlation between self-healing parameters and concludes that the self-healing area and the number of self-healing points are negatively correlated. Specifically, when the number of self-healing points in the effective area increases from 1 cm–2 to 30 cm–2, the average area of a single self-healing point decreases from 16 mm2 to 1 mm2. Furthermore, self-healing current peaks, self-healing time, and self-healing voltage are positively correlated. When the voltage reaches 3.5 kV, the self-healing time can reach 4 μs, and the self-healing current peak can reach 5 A. The self-healing energy follows a power function with an exponent of 2.316 relative to the self-healing voltage. Based on the established correlation between self-healing parameters, this paper also proposes a rapid estimation method for self-healing energy. The research involves key characteristic parameters and criteria for the performance of metallized film materials, providing valuable data supports for the optimized design of metallized film capacitors.
-
0. 引言
新能源电力系统是新时代国民经济的重要一环，柔性直流输电系统是新能源电力系统中的关键组成部分，承担着新能源送出、远距离大容量输电等任务[1]。换流阀是柔性直流输电系统的重要设备，其核心元件干式直流电容器起到滤波、电压支撑、阻尼缓冲、辅助环流等作用，决定着电能变换的质量与安全[2]。长期以来，国内的干式直流电容器的生产受制于国外公司，部分企业尚未掌握生产电容器所用薄膜原料的多尺度多维度综合评价技术，更多依赖于进口，导致国产电容器薄膜介电性能设计只能依靠过高的绝缘裕度来提高设备的可靠性，所研制的电容器尚处于实验验证和初步工程示范应用阶段，制约着我国特高压直流输电工程的发展。因此，对电容器用金属化膜进行必要的性能测试并了解其演变规律，对自主研制高端电容器，打破国外技术垄断，提升我国电力电子装备的创新能力和国际竞争力具有重要意义[3]。
干式直流电容器是一种金属化膜电容器，具有击穿后绝缘可恢复的自愈特性，即在薄膜的生产制造、运行过程中存在一些电弱点[4]，与邻近区域相比，这些电弱点处的击穿场强较低，在承受高电压时，电弱点处的介质膜被率先击穿并形成放电通道流经大电流，电流产生的热效应导致局部金属层受热蒸发形成等离子体并向外扩散，持续至能量低于临界值时，放电电弧难以维持并熄灭，膜间绝缘重新恢复[4-5]。自愈特性增强了电容器在高压、强脉冲作用下的可靠性及稳定性。
目前，国内外相关研究人员从自愈机理出发，对自愈行为特征及影响因素进行了大量研究，Kammermaier等提出自愈行为气体动力学理论，得到了自愈面积与击穿电压、电极厚度及电容量的关系[6]；Tortai等提出了判断自愈电弧熄灭的临界功率密度准则，并推导得出等离子体密度正比于层间压强的结论[4]；李化团队对自愈开展了较多研究，得到层间压强、方阻、电极参数、温度、热处理工艺等对金属化膜自愈特性的影响规律[7-11]；李志元[12]、杜一鸣[13]等从形貌出发，分别研究了电容器自愈对寿命的影响及劣化机理规律；李浩原[10]、Rytöluoto[14]、Belko[15]等对自愈参数的关联关系，尤其是自愈能量与自愈电压的关联指数进行了研究计算，为自愈能量耗散模型的建立提供了数据基础。以上工作均取得了成果，具有一定的指导意义，但对多物理场作用下的金属化膜自愈特性演变规律的研究较少。
本文基于课题研发的干式直流电容器实际运行工况，使用赛晶公司生产的某批次金属化聚丙烯薄膜，利用搭建的自愈测试平台，调节电-热-力参数模拟电容器的工况环境[16]，对金属化膜在多物理场下的自愈特性进行测试。通过试验数据统计分析，获得电场、温度、压强对自愈过程的影响规律，对相关的自愈参数构建关联关系，并提出了一种对自愈能量的快速估算方法，为金属化膜材料性能的关键特征参数和多维度综合评价方法提供数据参考。
1. 试验方法
1.1 试样制备
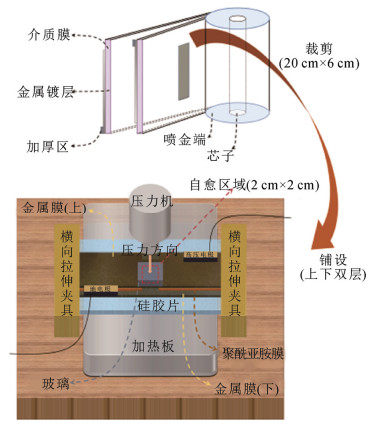
金属化膜电容器通常由两层单面蒸镀金属层的介质膜(一般为聚丙烯膜)围绕芯子卷绕而成，上下端面经过喷金处理后引出电极。在本试验中，为便于控制试验条件和实现自愈数据采集，从电容器中裁取2张长宽均为200 mm×50 mm的金属化膜并上下交叠铺设，两层金属化膜间布置两张聚酰亚胺薄膜以限制自愈区域，电容器及试样布置示意图见图 1。
1.2 试验条件
1.2.1 电场设置
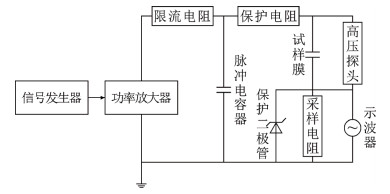
以课题研发的干式直流电容器额定工作电压直流2.8 kV为基准，设置5个等距电压等级：2.0、2.4、2.8、3.2、3.6 kV，试验时电压分别从零升至指定等级，升压速率参考《GB/T 13542.2—2021电气绝缘用薄膜第2部分：试验方法》[17]中的测试标准，结合预试验的测试结果，取为100 V/s，在升至指定电压等级后保持5 min。试验电路如图 2所示，其中信号发生器型号为RIGOL DG5071，输出频率70 MHz，采样率1 GHz；功率放大器为Trek Model 675型，放大倍数为1000；限流电阻为阻值10 MΩ的玻璃釉无感高压电阻；脉冲电容器为PULOM PCG-10 kV-1 μV型脉冲电容器；保护电阻为阻值100 Ω的无感纹波电阻；高压探针为HVP3220A型1 000:1固定衰减比无源探头，量程20 kV；保护二极管为2R075TB型陶瓷气体放电管，钳位电压75 V，可防止自愈失败时产生的过大电流损坏测量设备；采样电阻为阻值1 Ω的无感绕线电阻；示波器型号为TELEDYNE HDO6054，采样率10 GHz，用于监测采样电阻两端电压，进而计算出自愈发生时流经试品膜的自愈电流；导线采用直径6 mm的无感单股紫铜导线，以免线路电感对测量产生干扰。
1.2.2 温度设置
参考《GB/T 11024.1—2019标称电压1000 V以上交流电力系统用并联电容器第1部分：总则》[18]中的试验环境温度15~35 ℃，以及王子建[19]、陈麒任[20]等在Fluen和Comsol中的仿真分析结果，即电容器在实际运行时的最大温升在6~11 ℃之间，考虑排列布置方式及不同电场的温升效应，取20 ℃和45 ℃作为电容器运行温度的较低值和较高值。由于过高的温度会导致介质材料性能恶化，提高电容器故障概率[21]，参考《GB/T 11024.1》中规定的环境温度年平均最高上限5 5℃以及实际测量得到的电容器内部温度分布[22]，取70 ℃为电容器可长期连续工作的上限温度。综上，本试验设置20、45、70 ℃共3组温度条件。试验时，使用国辉JW-0510型恒温油浴循环器进行温控调节，在金属加热板上方铺设厚度为1 mm的硅胶片，起绝缘以及均衡压力的作用，试样置于硅胶片上方，温度由开普森HH-K-24型热电偶搭配ANTHONE LU-920S温控仪测量。
1.2.3 压强设置
金属化膜在绕制成电容器过程中受到轴向拉伸力及径向层间压力，绕制完成后最外层还会包裹若干层未蒸镀金属的介质膜以增大层间压力[7]。电容器不同层的金属化膜所受的拉伸力为恒定值，而层间压力逐层增大[10]。本试验所用金属化膜电容器绕制时的拉伸力由式(1)给出：
Td=kd0b (1) 式中：Td为卷绕时的拉伸力；k为拉伸系数，取值为1.3~1.5，试验中取k=1.5；d0=5.8 μm，表示膜厚；b=0.5 m，表示膜宽。计算得Td=4.35 N。
层间压强的计算式由式(2)[6]给出：
Pn=((2N−n)(Td+ηEsd0b)+2M(T1+ηEsd1b)b（r0+(n−1)d0）,n<2N(2N+2M−n)(T1+ηEsd1b)b（r0+(2N−1)d0+(n−2N)d1）,2N≤n<(2N+2M) (2) 式中：Pn为电容器自内向外至第n层处金属化膜受到的压强；2N为电容器金属化膜的层数，取5 000；Td取4.35 N；η为薄膜热处理后沿拉伸方向的热收缩率，取1.5%；Es为聚丙烯的杨氏模量，取180 N/mm2；d0=5.8 μm，表示膜厚；b=50 mm，表示膜宽；2M为最外层包裹膜的层数，取40；T1=Td=4.35N，表示外层包裹膜所受拉力；d1=5.8 μm，表示外层包裹膜的厚度；r0=9 mm，表示芯轴的直径。
利用式(2)可计算出不同的拉伸力-层间压强组合作用下，薄膜在电容器中的位置，因为电容器的轴向拉伸力为定值，本方案设置仅对径向的层间压力进行改变，考虑到式(2)理论计算值与实测值存在偏差，即在电容器的外层计算值与实测值符合的较好，越靠近内层计算值越高于实际值[6]，以及电容器拆解后的电容损耗统计显示电容器由自愈引起的电容损失集中在外层，内层的电容损失远小于外层的规律[23]，选择0.1 MPa(最外层)、0.5 MPa(深度3.6%)、1.2 MPa(深度8.3%)、2.5 MPa(深度16.2%)、4 MPa(深度24.1%)、8 MPa(深度40.7%)6组压强值进行试验，深度表示金属膜受到相应压强时在电容器中的位置。试验时，由特制夹具施加拉伸力并由量程0~1 kg的中诺ZN5H型拉力传感器进行测量，压力由量程2 000 kg的东日仪器DR-502AS型拉力试验机施加。
1.2.4 试验方案
通过5组电场值、3组温度值、6组压强值组合出90组不同的电-热-力条件，以实现多物理场效果，每组条件对30张试样进行试验，共进行2 700次试验。
2. 试验结果与分析
2.1 自愈后的试样观察
2.1.1 自愈数量
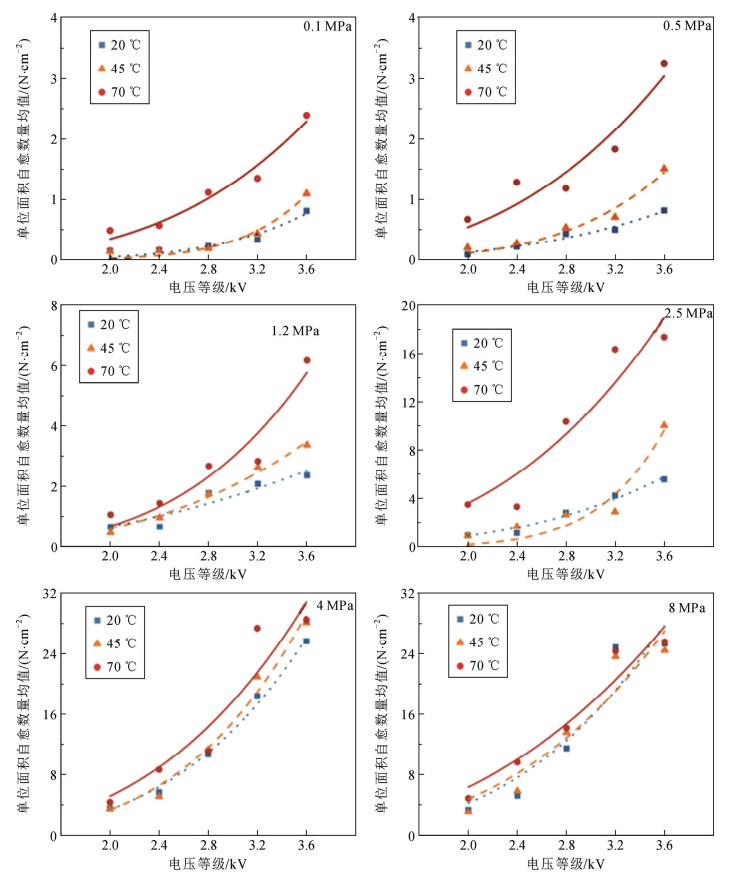
自愈次数的增加会引起电容器的容值下降，导致电容器的老化与寿命减少[24]，即自愈数量与电容器寿命呈负相关性，而固体绝缘寿命与外施电压符合反幂定律[25]，因此考虑对自愈数量与外施电压进行幂数拟合。统计试验后不同电-热-力条件下试样上的单位面积自愈数量均值(单位N/cm2)与自愈电压的关系如图 3并进行幂数拟合，可以看出在不同的热-力条件下，随着电压等级的升高，自愈数量均逐渐增大，且上升趋势与幂数关系相符。
![]()
图 3 不同压强下自愈数量均值与电压等级的关系Figure 3. Relationship between the average number of self-healing events and voltage levels under different pressures由图 3可见，电压、温度、压强对自愈数量的影响存在着复杂的交互作用。
1）在压强2.5 MPa及以下、电压2.8 kV及以下时，20 ℃和45 ℃对应的自愈数量均值较为接近，而70 ℃对应的自愈数量均值明显多于前2者，反映了电容器在低于工况电压2.8 kV运行时，高温(70 ℃)对电容器外层(深度16.2%以外)自愈数量的影响较大，低、中温(20 ℃、45 ℃)对电容器外层自愈数量的影响则无显著差异。
2）在压强2.5 MPa及以下、电压3.2 kV及以上时，低、中、高温对应的自愈数量均值区别较大，如在3.6 kV电压时，0.1、0.5、1.2、2.5 MPa这4种压强作用时，低、中、高温对应的自愈数量均值之比分别为1:1.36:2.97、1:1.84:3.99、1:1.42:2.61、1:1.80:3.11，不同温度造成的自愈数量均值均呈现明显差异，反映了电容器在高于工况电压2.8 kV运行时，不同运行温度对电容器外层(深度16.2%以外)自愈数量的影响具有显著差异。
3）在压强4 MPa及以上时，无论何种电压等级，低、中、高温对应的自愈数量均值较接近，幂函数拟合曲线也呈现相同上升趋势，说明高压强抑制了温度对电容器自愈数量的影响，反映了不同运行温度对电容器内层(深度24.1%以内)自愈数量无明显差异，且4 MPa与8 MPa的自愈数量均值接近，说明压强对自愈数量的影响存在瓶颈作用。
以上分析表明：控制电容器在合理的电压等级下运行，且维持器件内部温度场的良好分布，对其可靠稳定运行具有重要意义。
2.1.2 自愈面积
对自愈后的试样使用SOPTOP-SZN71型光学显微镜进行自愈数量和形貌的观察记录，在上下层膜均可观察到灰白色无固定形状的自愈区域。利用长度1 mm的标尺作参考进行拍摄，同一自愈点上下两层膜的自愈区域分别进行标定测量，二者之和即该自愈点的自愈面积。图 4给出了工况电压为2.8 kV、70 ℃、3组不同压强条件下试样自愈后的微观图，其中图 4(a)对上膜自愈点的击穿点进行了局部放大，图 4(b)和图 4(c)各选取一个自愈点进行自愈面积标注。可以看出，在压强较小时自愈面积较大，自愈形貌呈不规则杈状，可在上膜(接高压电极)观察到明显的击穿点，随着压强增大自愈面积逐渐减小，形貌也由杈状聚拢成团，上膜也不再能观察到明显的击穿点。
图 4中的面积代表金属膜在图示工况下典型自愈区域的大小。对不同电-热-力条件下的自愈面积进行统计分析，发现自愈面积与电压、温度呈正相关，与压强呈负相关，在相同电压水平下，压强较低时温度变化对自愈面积影响较大，而随着压强升高，温度变化对自愈面积影响不再显著，这一现象与自愈数量受温度、压强的影响具有相似性。将相同电-热-力条件下的自愈数量均值与自愈面积均值绘制如图 5并进行幂数拟合，可以看出自愈面积随自愈数量的增加呈幂数下降趋势，反映了在电容器自愈过程中，自愈数量N和自愈面积S间可能存在内在关联性，如何建立出更准确的表征关系有待进一步的探索。
![]()
图 5 自愈面积均值与自愈数量均值的散点图及拟合Figure 5. Scatterplot and fitting of mean area of self-healing and mean number of self-healing2.2 自愈参数
自愈现象的主要参数有自愈电压、自愈电流、自愈时间，及通过以上3个参数计算得到的自愈能量。典型自愈波形图如图 6。其中，U(t)为自愈电压，是自愈过程中试样两端的电压值，波形随时间通常呈先下降后上升的波动形式，为便于分析说明，一般以自愈初始时的电压稳定值表征自愈电压，而不考虑其在小范围内的波动；I(t)为自愈电流，是自愈过程中流经试品膜击穿点的电流，波形随时间通常呈现先上升后下降的波动形式，其中Im是自愈电流峰值，可以用来衡量自愈程度；T为自愈时间，是自愈电流从零开始上升至再次下降到零所持续的时间。自愈能量则通过计算自愈电压和自愈电流的乘积对自愈时间的积分得到。
2.2.1 自愈电压
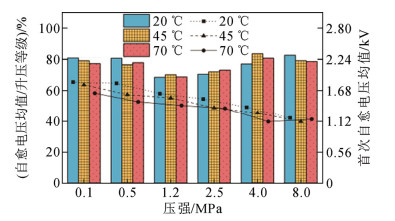
在试样两端电压稳定时，自愈电压为固定值，而在试样两端电压大范围变化时，自愈电压出现一定的随机性，目前对升压过程中自愈电压分布情况的研究较少，本节以工况电压等级2.8 kV为例，统计电压从0升至2.8 kV过程中试样的自愈电压、首次自愈电压随温度及压强的变化情况如图 7，其中柱状图表示升压过程中所有自愈点的自愈电压均值占升压等级的百分比，点线图表示升压过程中首次自愈点对应的首次自愈电压均值。
![]()
图 7 升压等级2.8 kV时不同压强下的自愈电压均值与首次自愈电压均值Figure 7. Mean values of self-healing voltage and first self-healing voltage at different pressures at step-up level 2.8 kV从图 7可以看出，温度与压强的变化对首次自愈电压产生影响：
1）首次自愈电压均值从20 ℃、0.1 MPa对应的最高值1.833 kV降至45 ℃、8 MPa对应的最低值1.113 kV，呈现持续下降趋势。
2）自愈电压均值维持在升压等级的70%~90%范围内。
3）首次自愈电压均值与自愈电压均值的差距呈递增趋势。这是由于低压强下自愈数量较少时，在所有自愈点中首次自愈点占比较大，当一张试样上有5个自愈点时，首次自愈点占所有自愈点的比例为1/5，此时在进行自愈电压均值计算时，首次自愈电压值贡献了较高的比重；而当一张试样上出现50个自愈点时，首次自愈点占所有自愈点的比例为1/50，此时首次自愈电压值对自愈电压均值计算的影响较低。压强升高时，首次自愈电压下降，同时自愈数量增多，自愈电压均值逐渐增大。
对其他升压等级下的试样进行同样分析，发现在温度、压强条件相同时，首次自愈电压均值在数值上均较接近，所有自愈电压均值都分布在升压等级的70%~90%范围内。可以认为，在电容器的升压启动过程中，首次自愈电压受温度和压强的影响较大，高温高压能够促进自愈的发生，而受升压等级的影响较小；自愈电压均值受温度和压强的影响相对较小，分布特性较大程度上取决于升压等级，并在升压等级一定比例范围内波动。
2.2.2 自愈电流峰值
为排除自愈电压对自愈电流的影响，统计自愈电压为2.8 kV时平均自愈电流峰值随温度、压强的变化规律如图 8所示，可以看出，平均自愈电流峰值随温度升高而增加、随压强的增大而减小，在20 ℃、8 MPa时自愈电流峰值最小值为0.403 A；在70 ℃、0.1 MPa时自愈电流峰值最大值为3.494 A，相较前者在数值上增长了767%，反映了自愈电流峰值受温度、压强的综合影响较大。不同压强下自愈电流峰值对温度的敏感性存在差异，如0.1 MPa时45 ℃、70 ℃的平均自愈电流峰值比20 ℃时分别增长136.1%、198. 4%，而8 MPa时45 ℃、70 ℃的平均自愈电流峰值比20 ℃时分别增长111.2%、161.8%，反映了在电容器的不同深度位置温度对金属化膜自愈电流影响的差异性：外层位置温度对自愈电流的影响显著性较大，越靠近内层温度对自愈电流的影响显著性越小。
![]()
图 8 自愈电压为2.8 kV时不同温度、压强下的平均自愈电流峰值Figure 8. Mean values of peak self-healing current at different temperatures and pressures at self-healing voltage of 2.8 kV为探究自愈电流峰值与自愈电压的关联性，随机抽取70 ℃、1.2 MPa、升压等级3.6 kV条件下的4组试样共92个自愈点，将其自愈电流峰值与自愈电压绘制于图 9，可以看出自愈电流峰值与自愈电压存在一定的正相关性，对其他条件下的试样进行相同分析可得类似结论，反映了在电容器实际运行过程中，控制电压运行等级可以一定程度上减小自愈电流。
![]()
图 9 自愈电流峰值与自愈电压散点图Figure 9. Scatter plot of peak self-healing current and self-healing voltage2.2.3 自愈时间
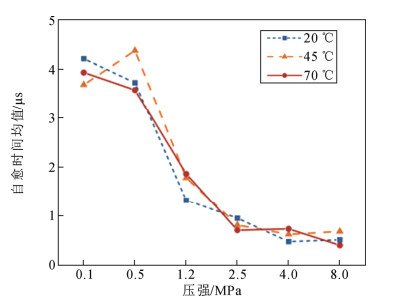
统计自愈电压2.8 kV时自愈时间均值随外施温度、压强的变化规律如图 10，可以看出，随着压强的增大，自愈时间均值逐渐减小，而温度与自愈时间均值未呈现出明显相关性。根据Kammermaier的自愈行为气体动力学理论[6]，自愈时间取决于自愈过程产生的等离子体的维持时间，当注入能量小于维持蒸发与电离金属电极能量时，等离子体开始熄灭，这一过程与电极材料、厚度和等离子体温度、电离度、压强等参数有关，Tortai的试验[4]进一步表明，等离子体放电熄灭的临界功率密度取决于外施的机械压力，且通过光谱测量得到自愈区域附近的温度约为7 200 K，自愈时间与压强的负相关性与上述自愈理论相符，而温度对自愈时间的无差异性可能是因为自愈中心的温度可达7 200 K，而3种实验设定温度与中心温度相差很大，作用有限。
![]()
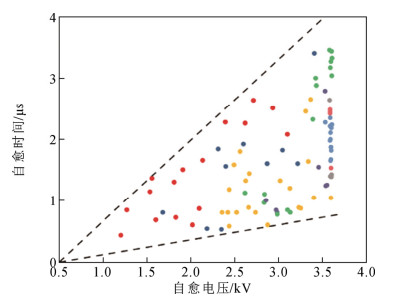
图 10 自愈电压为2.8 kV时不同温度、压强下的自愈时间均值Figure 10. Mean values of self-healing time at different temperatures and pressures at self-healing voltage of 2.8 kV为探究自愈时间与自愈电压的关联性，随机抽取70 ℃、1.2 MPa、升压等级3.6 kV条件下的4组试样共91个自愈点，将自愈时间与自愈电压绘制于图 11，可以看出自愈时间与自愈电压存在一定的正相关性，对其他条件下的试样进行相同分析可得类似结论，与Tortai[4]基于实验结果得到的自愈时间与自愈电压呈正相关性的结论相符，反映了在电容器实际运行过程中，合理的电压运行等级可以维持自愈持续时间在较小区间。
![]()
图 11 自愈时间与自愈电压散点图Figure 11. Scatter plot of self-healing time and self-healing voltage2.2.4 自愈能量
自愈能量是衡量自愈过程的关键性参数，不仅决定了自愈能否成功，还对金属化薄膜电容器的宏观特性及微观结构具有较大影响，是一个综合性的表征量。传统的自愈能量W计算式通常由自愈电压、自愈电流、自愈时间通过积分得出：
W=t∫0U(t)I(t)dt (3) 式(3)可计算出准确的自愈能量，但需先对自愈电压及自愈电流波形拟合以进行函数积分，拟合出的曲线存在误差且函数形式较复杂，或不拟合直接进行离散积分，考虑到示波器的采样间隔为0.4 ns，而自愈时间为微秒级，计算单次自愈点的自愈能量需处理几万到十几万行数据不等，两种方法的计算工作量均较大，数据处理过程耗时耗力。基于此提出一种对自愈能量的快速估算方法，具体形式如下：
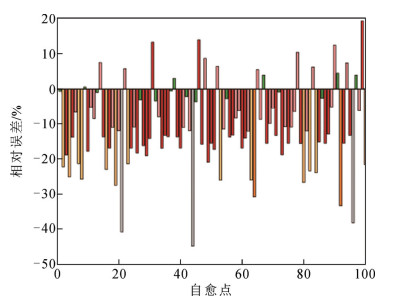
We=ζU0ImT2 (4) 式中：We为自愈能量；U0为自愈初始时试样两端的电压值，考虑到自愈过程中试样两端的电压波动较小，将式(3)中的自愈电压近似为固定值；ζ为优化系数，可在自愈能量的计算过程中不断迭代以减少估算误差。使用上述快速估算方法对随机抽取的100个自愈点进行估算并与真实值对比检验。当优化系数取1时，误差分布如图 12所示，相对误差在10%以内的数据有34个，10%~20%之间的有47个，20%~30%之间的有14个，超过30%的有5个，总体误差均值为13.767%。由于自愈波形随时间的分布形状多呈凸性，快速估算式仅考虑了始末点及最高点的内部连线三角形，造成大部分的估计值较真实值偏低，不断增大优化系数直至1.184，可使总体误差均值最小达4.753%，上述结果在一定程度上体现了估算式的合理性，在对精度要求不高的特定场合，可以利用估算方法替代传统的积分计算以实现对自愈能量的快速估计。
![]()
图 12 自愈能量估算值与真实值的相对误差分布Figure 12. Distribution of relative errors between estimated and true values of self-healing energyReed[27]、Rabuffi[28]等研究表明，自愈能量与工作电压、试品电容呈正相关性，与金属化膜方阻、层间压强呈负相关性，且层间压强对自愈的影响主要体现在通过影响金属化膜层间的空气密度，造成电场分布畸变，进而产生局部放电。李浩原[9]的实验结果显示，在相同的击穿场强下，自愈能量随温度的升高而增大。为对以上结论进行验证及进一步探索，本文统计了自愈电压为2.8 kV时自愈能量均值随温度、压强的变化规律(见图 13)，可以看出，相同温度条件下，随着压强的增大，自愈能量均值逐渐减小并趋于平稳，相同压强条件下，随着温度的升高自愈能量均值增大，在70 ℃、0.1 MPa时，自愈能量最大值达19.048 mJ，在20 ℃、8 MPa时，自愈能量最小值达0.695 mJ，比值达27.41，反映了温度、压强的复合作用对自愈能量的影响程度较大。20、45、70 ℃时不同压强下自愈能量均值的最大与最小值之比分别达12.997、16.455、22.021，此外在2.5 MPa以上时，所有温度条件下的自愈能量均值都在3 mJ以下，表明高压强可以有效限制自愈能量，防止过大的自愈能量可能导致的自愈失败[29]。
![]()
图 13 自愈电压2.8 kV时不同温度、压强下的自愈能量均值Figure 13. Mean values of self-healing energy at different temperatures and pressures at self-healing voltage of 2.8 kV自愈能量与自愈电压间存在近似的幂数关系，Kammermaier的试验结果表明，自愈能量近似等于自愈电压的4次方[6]，Tortai[4]的结果为6次方，Belko的结果为6.1次方[30]，李浩原的结果则在2.4~2.7次方[10]，具体系数取决于金属化膜的材料性质及外施物理场条件。为探究自愈能量与自愈电压的关联性，随机抽取70 ℃、1.2 MPa、升压等级3.6 kV条件下的4组试样共107个自愈点，将自愈能量与自愈电压绘制于图 14，可以看出自愈能量随自愈电压的增加呈幂数增长趋势，其中拟合函数的幂指数为2.316，拟合优度为0.729。对其他条件下的试样进行相同计算，得到的幂指数介于2.031~2.758之间，反映了在电容器自愈过程中自愈能量与自愈电压间的内在关联性。
![]()
图 14 自愈能量与自愈电压的散点图及拟合Figure 14. Scatterplot and fitting of self-healing energy and self-healing voltageWalgenwitz的研究表明，自愈能量通常是金属层蒸发焦耳热的3~4倍，而金属层的蒸发程度与自愈面积相关[31]，因此自愈能量与自愈面积间存在一定的关联关系，Tortai[4]、Reed[27]、章妙[23]等的试验结果显示，自愈能量与自愈面积呈线性正比关系。将107个自愈点的自愈能量与自愈面积绘制成散点图并进行线性拟合，见图 15，可看出随自愈能量增大自愈面积呈线性增加趋势，拟合优度为0.758，与前人的结果相符，对其他条件下的试样进行计算得到的拟合公式系数有差异，可能是由于不同条件下金属化膜自愈时不同电弧行为导致，此外，蒸发金属层的厚度将间接影响薄膜表面金属层电弧蒸发导致的去金属化程度，进而对自愈能量造成影响[29, 32-33]。
![]()
图 15 自愈面积与自愈能量的散点图及拟合Figure 15. Scatterplot and fitting of self-healing area and self-healing energy3. 结论
本文设计了多物理场作用下的金属化膜自愈特性试验，通过调节电-热-力参数模拟了不同的电容器运行工况条件，统计了金属化膜自愈后的数量、面积、自愈参数的分布特点以及随物理场的变化规律，建立了一些统计量的关联关系，并提出了一种对自愈能量的快速估算方法，得出以下结论：
1）电压、温度、压强对金属化膜自愈的影响存在交互作用，温度、压强不变时，自愈数量、自愈面积、升压过程中的自愈电压均值、自愈电流峰值、自愈时间、自愈能量与电压呈正相关性；电压、压强不变时，自愈数量、自愈面积、自愈电流峰值、自愈能量与温度呈正相关性，首次自愈电压与温度呈负相关性，自愈时间与温度无明显相关性；电压、温度不变时，自愈数量与压强呈正相关性，自愈面积、首次自愈电压、自愈电流峰值、自愈时间、自愈能量与压强呈负相关性。升压过程中的自愈电压均值分布于升压等级的70%~90%范围内。
2）在自愈电压为2.8 kV时，金属化膜的自愈数量、自愈面积、自愈电流峰值、自愈能量在不同压强下对温度呈现出不同的敏感性，随着压强的增大，在20、45、70 ℃这3种温度下上述自愈表征量的比值逐渐减小，表明在压强高于特定临界值时，对自愈的影响比温度更具主导性。
3）金属化膜的一些自愈表征量间存在关联性，自愈面积和自愈数量呈负相关性；自愈电流峰值、自愈时间与自愈电压呈正相关性；自愈能量与自愈电压呈幂值函数关系，且幂指数介于2.031~2.758；自愈能量与自愈面积呈线性上升关系。表明运行于合理的电压等级、改善电容器内部温度压强分布，能够有效控制自愈能量，防止自愈失败。
-
![]()
图 3 不同压强下自愈数量均值与电压等级的关系
Figure 3. Relationship between the average number of self-healing events and voltage levels under different pressures
![]()
图 5 自愈面积均值与自愈数量均值的散点图及拟合
Figure 5. Scatterplot and fitting of mean area of self-healing and mean number of self-healing
![]()
图 7 升压等级2.8 kV时不同压强下的自愈电压均值与首次自愈电压均值
Figure 7. Mean values of self-healing voltage and first self-healing voltage at different pressures at step-up level 2.8 kV
![]()
图 8 自愈电压为2.8 kV时不同温度、压强下的平均自愈电流峰值
Figure 8. Mean values of peak self-healing current at different temperatures and pressures at self-healing voltage of 2.8 kV
![]()
图 9 自愈电流峰值与自愈电压散点图
Figure 9. Scatter plot of peak self-healing current and self-healing voltage
![]()
图 10 自愈电压为2.8 kV时不同温度、压强下的自愈时间均值
Figure 10. Mean values of self-healing time at different temperatures and pressures at self-healing voltage of 2.8 kV
![]()
图 11 自愈时间与自愈电压散点图
Figure 11. Scatter plot of self-healing time and self-healing voltage
![]()
图 12 自愈能量估算值与真实值的相对误差分布
Figure 12. Distribution of relative errors between estimated and true values of self-healing energy
![]()
图 13 自愈电压2.8 kV时不同温度、压强下的自愈能量均值
Figure 13. Mean values of self-healing energy at different temperatures and pressures at self-healing voltage of 2.8 kV
![]()
图 14 自愈能量与自愈电压的散点图及拟合
Figure 14. Scatterplot and fitting of self-healing energy and self-healing voltage
-
[1] 雷万钧, 刘进军, 吕高泰, 等. 大容量电力电子装备关键器件及系统可靠性综合分析与评估方法综述[J]. 高电压技术, 2020, 46(10): 3353-3361. DOI: 10.13336/j.1003-6520.hve.20201143 LEI Wanjun, LIU Jinjun, LÜ Gaotai, et al. Review of reliability comprehensive analysis and evaluation methods for key components and system of large capacity power electronic equipment[J]. High Voltage Engineering, 2020, 46(10): 3353-3361. DOI: 10.13336/j.1003-6520.hve.20201143
[2] 戴志辉, 刘宁宁, 何永兴, 等. 基于直流滤波环节暂态能量比的高压直流线路纵联保护[J]. 电工技术学报, 2020, 35(9): 1985-1998. DAI Zhihui, LIU Ningning, HE Yongxing, et al. A pilot protection for HVDC transmission lines based on the ratio of DC filter link transient energy[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1985-1998.
[3] 何晓靓, 高琪, 刘水平, 等. 大容量柔性直流输电工程用直流支撑电容器技术研究[J]. 电力电容器与无功补偿, 2020, 41(4): 81-85. HE Xiaoliang, GAO Qi, LIU Shuiping, et al. Study on DC support capacitor technology for high power flexible DC transmission project[J]. Power Capacitor & Reactive Power Compensation, 2020, 41(4): 81-85.
[4] TORTAI J H, DENAT A, BONIFACI N. Self-healing of capacitors with metallized film technology: experimental observations and theoretical model[J]. Journal of Electrostatics, 2001, 53(2): 159-169. DOI: 10.1016/S0304-3886(01)00138-3
[5] TORTAI J H, BONIFACI N, DENAT A, et al. Self-healing of aluminium metallized polypropylene films: a spectroscopic investigation[C]∥IEEE 14th International Conference on Dielectric Liquids. Graz, Austria: IEEE, 2002: 190-193.
[6] KAMMERMAIER J, RITTMAYER G, BIRKLE S. Modeling of plasma-induced self-healing in organic dielectrics[J]. Journal of Applied Physics, 1989, 66(4): 1594-1609. DOI: 10.1063/1.344373
[7] LI Z W, LI H, LIN F C, et al. Lifetime improvement of metallized film capacitors by inner pressure strengthening[J]. IEEE Transactions on Plasma Science, 2013, 41(10): 3063-3068. DOI: 10.1109/TPS.2013.2279140
[8] CHEN Y H, LI H, LIN F C, et al. Effect of interlayer air on performance of dry-type metalized film capacitor in DC, AC and pulsed applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011, 18(4): 1301-1306. DOI: 10.1109/TDEI.2011.5976131
[9] LI H Y, LI H, LI Z W, et al. Temperature dependence of self-healing characteristics of metallized polypropylene film[J]. Microelectronics Reliability, 2015, 55(12): 2721-2726. DOI: 10.1016/j.microrel.2015.09.007
[10] 李浩原. 应用于电力系统的干式金属化膜电容器性能研究[D]. 武汉: 华中科技大学, 2016. LI Haoyuan. Research on performance of dry type metallized film capacitors applied in power system[D]. Wuhan, China: Huazhong University of Science and Technology, 2016.
[11] 李化, 章妙, 林福昌, 等. 金属化膜电容器自愈理论及规律研究[J]. 电工技术学报, 2012, 27(9): 218-223, 230. LI Hua, ZHANG Miao, LIN Fuchang, et al. Study on theory and influence factors of self-healing in metallized film capacitors[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 218-223, 230.
[12] 李志元, 王镜然, 徐哲, 等. 直流电压作用下金属化膜电容器的自愈特性及寿命预测[J]. 高电压技术, 2023, 49(7): 2929-2937. DOI: 10.13336/j.1003-6520.hve.20221549 LI Zhiyuan, WANG Jingran, XU Zhe, et al. Self-healing characteristics and life prediction of metallized film capacitor under DC voltage[J]. High Voltage Engineering, 2023, 49(7): 2929-2937. DOI: 10.13336/j.1003-6520.hve.20221549
[13] 杜一鸣, 潘亮, 祝令瑜, 等. 金属化膜电容器交流和直流电压劣化特性分析[J]. 电力工程技术, 2020, 39(6): 151-158. DU Yiming, PAN Liang, ZHU Lingyu, et al. AC and DC voltage degradation characteristics of metallized film capacitors[J]. Electric Power Engineering Technology, 2020, 39(6): 151-158.
[14] RYTÖLUOTO I, LAHTI K, KARTTUNEN M, et al. Large-area dielectric breakdown performance of polymer films - part Ⅰ: measurement method evaluation and statistical considerations on area-dependence[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(2): 689-700. DOI: 10.1109/TDEI.2015.7076764
[15] BELKO V O, EMELYANOV O A, IVANOV I O, et al. Self-healing processes of metallized film capacitors in overload modes-part 1: experimental observations[J]. IEEE Transactions on Plasma Science, 2021, 49(5): 1580-1587. DOI: 10.1109/TPS.2021.3071187
[16] 杨帆, 郝翰学, 王鹏博, 等. 电力装备多物理场数值计算发展现状[J]. 高电压技术, 2023, 49(6): 2348-2364. DOI: 10.13336/j.1003-6520.hve.20231105 YANG Fan, HAO Hanxue, WANG Pengbo, et al., State of the art of multiphysics simulation technology for power equipment[J]. High Voltage Engineering, 2023, 49(6): 2348-2364. DOI: 10.13336/j.1003-6520.hve.20231105
[17] 国家市场监督管理总局, 国家标准化管理委员会. 电气绝缘用薄膜第2部分: 试验方法: GB/T 13542.2—2021[S]. 北京: 中国标准出版社, 2021. State Administration for Market Regulation, National Standardization Administration. Plastic films for electrical purposes-part 2: methods of test[S]. Beijing, China: Standards Press of China, 2021.
[18] 国家市场监督管理总局, 国家标准化管理委员会. 标称电压1 000 V以上交流电力系统用并联电容器第1部分: 总则: GB/T 11024.1—2019[S]. 北京: 中国标准出版社, 2019. State Administration for Market Regulation, National Standardization Administration. Shunt capacitors for AC power systems having a rated voltage above 1 000 V-part 1: general[S]. Beijing, China: Standards Press of China, 2019.
[19] 尹婷, 王子建, 侯智剑, 等. 环境温度及施加电压对自愈式电力电容器温升和温度场分布的影响[J]. 科学技术与工程, 2016(1): 193-199, 203. DOI: 10.3969/j.issn.1671-1815.2016.01.037 YIN Ting, WANG Zijian, HOU Zhijian, et al. Influence of ambient temperature and applied voltage on the temperature rise and temperature distribution of self-healing power capacitor[J]. Science Technology and Engineering, 2016(1): 193-199, 203. DOI: 10.3969/j.issn.1671-1815.2016.01.037
[20] 李化, 陈麒任, 李浩原, 等. 交流高压金属化膜电容器温升特性和优化设计[J]. 高压电器, 2018, 54(1): 1-8. LI Hua, CHEN Qiren, LI Haoyuan, et al. Temperature rise characteristic and design optimization of AC high voltage metallized film capacitor[J]. High Voltage Apparatus, 2018, 54(1): 1-8.
[21] 马乃兵. 干式高压并联电容器的技术特点分析[J]. 电力电容器, 2002(2): 7-10. DOI: 10.3969/j.issn.1674-1757.2002.02.003 MA Naibing. Analysis of the technical characteristics for the dry-type high-voltage shunt capacitor[J]. Power Capacitors, 2002(2): 7-10. DOI: 10.3969/j.issn.1674-1757.2002.02.003
[22] 岳国华, 杜志叶, 孟圣淳, 等. 基于电热耦合的干式直流电容器温升分布不均匀特性分析及优化[J]. 高电压技术, 2022, 48(12): 4915-4924. DOI: 10.13336/j.1003-6520.hve.20220906 YUE Guohua, DU Zhiye, MENG Shengchun, et al. Analysis and optimization of non-uniform temperature rise distribution of dry-type DC capacitor based on electro-thermal coupling[J]. High Voltage Engineering, 2022, 48(12): 4915-4924. DOI: 10.13336/j.1003-6520.hve.20220906
[23] 章妙. 金属化膜电容器自愈特性研究[D]. 武汉: 华中科技大学, 2012. ZHANG Miao. Study on the characteristics of self-healing in metallized film capacitors[D]. Wuhan, China: Huazhong University of Science and Technology, 2012.
[24] 王文娟, 李化, 李智威, 等. 通过电容器层间压强的增强提高电容器寿命[J]. 强激光与粒子束, 2014, 26(4): 045015. WANG Wenjuan, LI Hua, LI Zhiwei, et al. Lifetime improvement of metallized film capacitors by inner pressure strengthening[J]. High Power Laser and Particle Beams, 2014, 26(4): 045015.
[25] 徐哲, 程璐, 刘宏博, 等. 超高直流电场作用下金属化膜电容器的老化特性[J]. 绝缘材料, 2023, 56(5): 55-62. XU Zhe, CHENG Lu, LIU Hongbo, et al. Ageing characteristics of metallized film capacitor under ultra-high DC field[J]. Insulating Materials, 2023, 56(5): 55-62.
[26] 沈其工. 高电压技术[M]. 北京: 中国电力出版社, 2012. SHEN Qigong. High voltage technology[M]. Beijing, China: China Electric Power Press, 2012.
[27] REED C W, CICHANOWSKIL S W. The fundamentals of aging in HV polymer-film capacitors[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1994, 1(5): 904-922. DOI: 10.1109/94.326658
[28] RABUFFI M, PICCI G. Status quo and future prospects for metallized polypropylene energy storage capacitors[J]. IEEE Transactions on Plasma Science, 2002, 30(5): 1939-1942. DOI: 10.1109/TPS.2002.805318
[29] 李黎, 林福昌, 李劲, 等. 高场强下金属化膜电容器自愈失败的原因[J]. 高电压技术, 2001, 27(1): 45-46. DOI: 10.3969/j.issn.1003-6520.2001.01.017 LI Li, LIN Fuchang, LI Jin, et al. Discussion on reasons of metallixed film capacitors self-healing failure under high electric stress[J]. High Voltage Engineering, 2001, 27(1): 45-46. DOI: 10.3969/j.issn.1003-6520.2001.01.017
[30] BEL'KO V O, BONDARENKO P N, EMEL'YANOV O A. The dynamic characteristics of self-healing processes in metal film capacitors[J]. Russian Electrical Engineering, 2007, 78(3): 138-142.
[31] WALGENWITZ B, TORTAI J H, BONIFACI N, et al. Self-healing of metallized polymer films of different nature[C]//2004 IEEE International Conference on Solid Dielectrics. Toulouse, France: IEEE, 2004: 29-32.
[32] 李琦, 李曼茜. 高温聚合物薄膜电容器介电材料评述与展望[J]. 高电压技术, 2021, 47(9): 3105-3123. DOI: 10.13336/j.1003-6520.hve.20210715 LI Qi, LI Manxi. High-temperature polymer dielectrics for film capacitors: review and prospect[J]. High Voltage Engineering, 2021, 47(9): 3105-3123. DOI: 10.13336/j.1003-6520.hve.20210715
[33] 张凡, 吴书煜, 徐征宇, 等. 变压器绕组非线性动力学模型及多次短路冲击下的振动特征[J]. 高电压技术, 2022, 48(12): 4882-4892. DOI: 10.13336/j.1003-6520.hve.20220499 ZHANG Fan, WU Shuyu, XU Zhengyu, et al. Nonlinear dynamics model of transformer winding and vibration characteristics under multiple short-circuit shocks[J]. High Voltage Engineering, 2019, 48(12): 4882-4892. DOI: 10.13336/j.1003-6520.hve.20220499
下载:
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
下载:
