牵引网短路故障下的车体电位及车体回流分布特性

周福林; 陈明辉; 熊进飞; 马孟阳

doi:10.13336/j.1003-6520.hve.20210439

牵引网短路故障下的车体电位及车体回流分布特性

西南交通大学电气工程学院, 成都 610031

基金项目:

国家重点研发计划 VP99QT1104Y17002

详细信息

通讯作者:
周福林(通信作者)，1982—，男，博士，副教授，主要从事电能质量分析与控制、轨道交通车网耦合分析的研究，E-mail: fulin-zhou@swjtu.edu.cn

计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2021-03-21
- 修回日期: 2021-07-05
- 刊出日期: 2022-04-29

Train Body Potential and Body Return Current Distribution Characteristics Under Short Circuit Fault of Traction Network

School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China

Funds:

National Key R & D Program of China VP99QT1104Y17002

More Information

Corresponding author:
ZHOU Fulin, Ph.D., Assoicate professor, Corresponding author

摘要

摘要: 牵引网发生短路故障时，短路大电流会引起列车车体电位和车体回流显著增大，进而对人身安全和车载电气设备正常工作造成威胁。为准确掌握短路工况下车体电位和车体回流的分布大小，需考虑牵引网与列车接地回路间的感性耦合。为此结合牵引供电系统分析和工程电磁场理论，推导了接地回路中传导电流及感应电流的相量表达式，从理论上证明了考虑感性耦合会增大车体电位及车体回流。利用建立的车–网–地耦合模型，进行仿真计算并与实测数据对比，得出：考虑感性耦合下的车体对轴端电位差仿真值比实测值小1.04 V，误差为8.9%；不考虑感性耦合下的仿真值比实测值小6.30 V，误差为54.0%，验证了理论分析的正确性。最后利用考虑感性耦合的仿真模型进行车体电位及车体回流分布特性的研究，结果表明：车体对轴端电位差主要受短路点位置和列车位置的影响；车体对地电位主要受钢轨泄漏电阻的影响；车体回流主要受车体对轴端等效电阻的影响。
- 牵引网短路 /
- 车体电位 /
- 车体回流 /
- 感性耦合 /
- 车–网–地耦合模型
Abstract: When a short-circuit fault occurs in the traction network, the short-circuit will cause a significant increase in the train body potential and return current, which will threaten the personal safety and normal operation of on-board electrical equipment. In order to accurately grasp the distribution of train body potential and return current under short-circuit conditions, it is necessary to consider the inductive coupling between the traction network and the train ground loop. Based on the analysis of traction power supply system and engineering electromagnetic field theory, this paper derives the phasor expressions of conduction current and induced current in the ground loop, and theoretically proves that considering inductive coupling will increase the body potential and return of the body. The established train-network-ground coupling model is adopted to perform the the simulation calculation and the comparison with the measured data, and the results show that the simulation value of the train body to wheel potential difference considering the inductive coupling is 1.04 V smaller than the measured value, and the error is 8.9%. The simulated value under inductive coupling is 6.30 V smaller than the measured value, and the error is 54.0%, which verifies the correctness of the theoretical analysis. Finally, a simulation model considering inductive coupling is used to study the train body potential and body return distribution characteristics. The results show that the potential difference between the train body and the wheel is mainly affected by the position of the short-circuit point and the train position, the ground potential of the car body is mainly affected by the rail leakage resistance, and the train body return is mainly affected by the equivalent resistance of the train body to the wheel.
- traction network short circuit /
- train body potential /
- train body current return /
- inductive coupling /
- train-network-ground coupling model

HTML全文

0. 引言

随着我国电气化铁路的不断发展，电力机车和动车组(下文统称列车)的安全稳定运行受到人们高度重视^[1-3]。车载电气设备、车内控制系统、通信系统等设备的地电位均以车体电位作为参考，使得车体电位和车体回流成为影响列车运行安全的重要因素之一^[4-5]。与列车正常运行工况相比，短路工况具有明显的大电流、强磁场特征，当发生短路时，钢轨上的短路电流会经列车保护接地分流至车体，使车体电位和车体回流显著增大。而车体对轴端电位差过大易导致转向架上速度传感器、温度传感器出现误差甚至损坏^[6]，列车接地回流过大易导致轴承电蚀^[7]。因此，研究短路大电流下车体电位和车体回流的分布特性，对保证列车的安全运行及乘客安全具有重要意义。

针对车体电位和车体回流问题，国内外相关学者进行了大量的研究。车体回流方面，文献[8]指出电流通过列车轴承时易造成轴承电蚀，并通过试验提供了轴承的保护措施。文献[9]介绍了一种新的组合型接地装置，新接地装置能有效减小流经轴承的电流，延长轴承的使用寿命。文献[10]阐述了车体地电流的来源，并通过仿真和试验分析了地电流在车体壳体及车载设备机柜上的传播特性。文献[11-12]利用PSPICE搭建了动车组接地系统模型，仿真分析接地方式不同对列车接地回流的影响，并提出增大接地电阻来抑制钢轨电流流入车体。车体电位方面，文献[13]仿真分析了列车接地技术对车体过电压的影响规律，并给出动车组过分相时接地技术的建议。文献[14-16]分析浪涌对车体电位的影响机理，认为保护接地方式和车顶高压电缆与车体的耦合电容将极大的影响车体电位，并提出降低车体电位的理想接地系统。文献[17]分析了离线电弧对车体电位的影响及车体电位对速度传感器的干扰机理。文献[18]针对雷击T线、F线和雷电流幅值不同等工况，开展了车体过电压分布规律的研究。文献[19]对接触网中的雷电流在车体–接地系统–钢轨局部接地回路中产生的感应电压进行分析。

总结来说，根据国内外研究现状，车体电位和车体回流分布特性及抑制方法的研究主要集中在列车正常运行、过分相、升降弓和离线工况下，而关于短路工况下的研究尚处于空白阶段。列车在实际运行中，车体–保护接地–钢轨之间会形成局部接地回路，依据电磁场理论^[20]，由牵引网多导体上的短路电流激发的工频磁场将在接地回路中产生感应电流。文献[21-22]根据毕奥–萨伐尔定律，对短路点附近的磁场分布进行了计算。文献[23]分别对考虑和不考虑车–网间感性耦合的情况进行仿真分析，指出列车在升弓和降弓工况下，考虑感性耦合对车体电位和车体回流是抑制作用，而在过分相工况为抬升作用，但并未给出考虑感性耦合造成车体电位、车体回流增大或减小的具体原因。

鉴于此，本文结合牵引供电系统分析和工程电磁场理论，推导了短路工况下列车接地回路中传导电流和感应电流的相量表达式，基于两者间的相位关系得出考虑车–网间感性耦合总是具有增大车体回流和车体电位的作用。以某列车接地系统为例，建立了车–网–地耦合模型，通过仿真计算与实测数据的对比，验证了考虑感性耦合不仅对车体电位及车体回流有抬升作用且实际值更相符，并利用仿真进一步分析了短路工况下车体电位(车体电位代表车体对轴端电位差和车体对地电位两部分)及车体回流的分布大小和影响因素。

1. 车–网系统间电气耦合机理分析

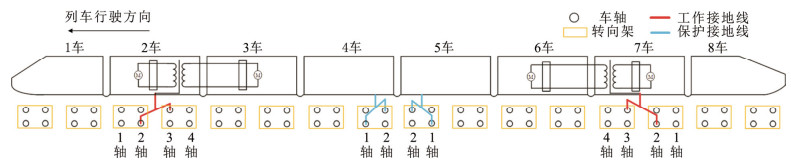
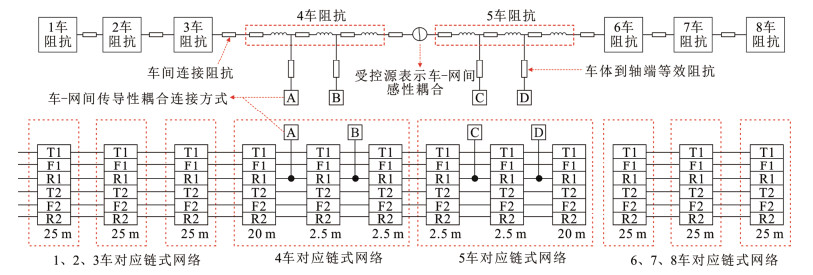
某列车接地系统如图 1所示，其接地系统按功能可分为工作接地和保护接地。工作接地点设置在2车2轴左侧(以面向列车行驶方向为参考)、3轴右侧和7车2轴左侧、3轴右侧，工作接地的作用为将来自接触网的电流反馈到轨道上。保护接地点设置在4车1轴左侧、2轴右侧和5车1轴左侧、2轴右侧，保护接地点通过软连线与转向架构架和车体相连(图 1中用车体与保护接地点直接连接来等效表示)，同时各车厢间通过连接线等电位连接，从而保证整车车体电位稳定。

图 1 某列车接地系统方式

Figure 1. A train grounding system method

下载: 全尺寸图片幻灯片

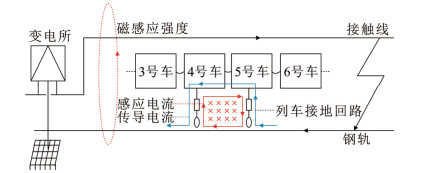
当牵引网发生接触线对钢轨(下文简称为T–R)短路故障时，钢轨上的短路电流从下往上经保护接地流入车体，进而产生车体电位和车体回流，这一部分称为车–网系统间的传导性耦合。同时，牵引网多导体中的电流在空间产生工频磁场，该磁场会在列车接地回路(接地回路由车体–保护接地–钢轨构成)中产生感应电流，这一部分称为车–网系统间的感性耦合。因此，车体电位和车体回流可看作车–网系统传导性耦合和感性耦合叠加作用的结果(下文建模时还考虑了钢轨对地泄漏电阻的影响，即称为车–网–地耦合系统)，车–网系统间电气耦合关系如图 2所示。

图 2 车–网系统间电气耦合关系

Figure 2. Electrical coupling relationship between train-network systems

下载: 全尺寸图片幻灯片

1.1 传导性耦合

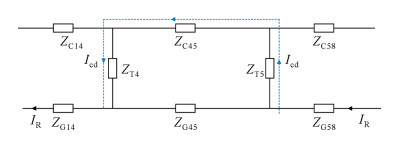
通过建立列车接地回路的等效模型来推导车体传导电流表达式。接地回路主要由车体阻抗、车体对轴端等效阻抗(该等效阻抗包括软连线阻抗、碳刷阻抗及接触阻抗)和钢轨阻抗3部分组成。由于该型列车在4车1、2轴和5车1、2轴设置了保护接地，使得4车车体对4车1、2轴和5车车体对5车1、2轴的等效阻抗仅有几十毫欧，而其它车厢对各自车轴轴端的等效阻抗基本在数千欧。因此，为方便分析，仅计及4车车体对4车1、2轴和5车车体对5车1、2轴的等效阻抗，其他车厢与钢轨间的阻抗认为无穷。若假设车体单位长度阻抗处处相等，则可将1车端部至4车1轴这段长度的车体阻抗等效为Z_C14，钢轨阻抗等效为Z_G14；同理，将4车1轴至5车1轴这段长度的车体阻抗等效为Z_C45，钢轨阻抗等效为Z_G45；将5车1轴至8车端部这段长度的车体阻抗等效为Z_C58，钢轨阻抗等效为Z_G58；并将4车车体对4车1轴与4车2轴的等效阻抗合并为Z_T4，5车车体对5车1轴与5车2轴的等效阻抗合并为Z_T5。基于上述等效思想，建立的列车接地回路等效模型如图 3所示，I_R表示钢轨电流，I_cd为流入车体的传导电流。图 3模型中忽略钢轨对地泄漏电阻的影响。

图 3 列车接地回路等效模型

Figure 3. Equivalent model of train ground loop

下载: 全尺寸图片幻灯片

依据基尔霍夫定律，可计算流入车体的传导电流表达式为

$I_{\mathrm{cd}}=\frac{Z_{\mathrm{G} 45}}{Z_{\mathrm{G} 45}+\left(Z_{\mathrm{T} 4}+Z_{\mathrm{T} 5}+Z_{\mathrm{C} 45}\right)} I_{R}$

(1)

由式(1)可知，流入车体的传导电流I_cd大小取决于I_R、Z_G45、Z_T4、Z_T5及Z_C45。其中，外部系统容量、变压器型号、牵引网导线参数确定后，I_R值主要与短路方式及短路点位置有关，而Z_G45、Z_T4、Z_T5及Z_C45值相对稳定。

1.2 感性耦合

以直供带回流线的供电方式为例，说明牵引网在列车接地回路中产生的感应电流大小。依据工程电磁场理论，闭合回路中感应电压的大小等于载流导体与回路之间交链的磁链对时间的导数，且感应电流大小等于感应电压与回路阻抗的比值。利用叠加原理，分别计算出各导线单独作用时在接地回路中产生的感应电流，通过规定感应电流的正方向，矢量叠加可计算出整体牵引网在接地回路中产生的感应电流大小和方向。

首先，分析接触线单独作用在接地回路中产生感应电流大小。假设接触线电流表达式为

$I_{\mathrm{t}}(t)=\sqrt{2} I_{1} \sin \left(\omega t+\theta_{1}\right)$

(2)

式中：I₁为接触线电流有效值；ω为电流角频率；θ₁为接触线电流初相位。

地面上载流导线产生磁场的精确计算需要考虑地中镜像电流对磁场的影响，但由于镜像导体的等效深度远大于载流导线的高度，故计算时忽略镜像导体的影响。接触线单独作用时在接地回路产生的磁场如图 4(a)所示，依据安培环路定律，得出接地回路中任一点P的磁感应强度为

$B_{1}(x, t)=\frac{\sqrt{2} \mu_{0} I_{1}}{2 {\rm{ \mathsf{ π} }} x} \sin \left(\omega t+\theta_{1}\right)$

(3)

图 4 牵引网各导线作用下的接地回路磁场分布

Figure 4. Distribution of magnetic field in ground loop under the action of conductors in traction network

下载: 全尺寸图片幻灯片

式中：μ₀为真空磁导率；x为点P与接触线的垂直距离。

如图 4(a)所示，列车车体底部与接触线的垂直距离为x₁，轮对与接触线的垂直距离为x₂，接地回路长度为l。则接触线与接地回路交链的磁链为

$\psi_{1}(t)=\frac{\sqrt{2} \mu_{0} I_{1}}{2 {\rm{ \mathsf{ π} }}} \int_{x_{1}}^{x_{2}} \frac{l}{x} \sin \left(\omega t+\theta_{1}\right) \mathrm{d} x$

(4)

感应电压大小等于磁链对时间的导数，感应电压表达式为

$e_{1}=-\frac{\mathrm{d} \psi(t)}{\mathrm{d} t}=\frac{\sqrt{2} \mu_{0} \omega I_{1}}{2 {\rm{ \mathsf{ π} }}} \int_{x_{1}}^{x_{2}} \frac{l}{x} \sin \left(\omega t+\theta_{1}-\frac{{\rm{ \mathsf{ π} }}}{2}\right) \mathrm{d} x$

(5)

则接触线电流及接触线单独作用时在接地回路中产生的感应电压相量形式为

$\left\{\begin{array}{l} \boldsymbol{I}_{\mathrm{t}}=I_{1} \angle \theta_{1} \\ \boldsymbol{e}_{1}=\frac{\mu_{0} \omega I_{1} l}{2 {\rm{ \mathsf{ π} }}} \ln \frac{x_{2}}{x_{1}} \angle\left(\theta_{1}-\frac{{\rm{ \mathsf{ π} }}}{2}\right) \end{array}\right.$

(6)

列车接地回路中各部分阻抗如图 3所示。定义接地回路阻抗为

$Z_{\mathrm{cir}}=Z_{\mathrm{T} 4}+Z_{\mathrm{T} 5}+Z_{\mathrm{C} 45}+Z_{\mathrm{G} 45}=Z_{0} \angle \theta_{0}$

(7)

则接触线在接地回路中产生感应电流I_gy1的相量形式为

$\boldsymbol{I}_{\mathrm{gy} 1}=\frac{\mu_{0} \omega I_{1} l}{2 {\rm{ \mathsf{ π} }} Z_{0}} \ln \frac{x_{2}}{x_{1}} \angle\left(\theta_{1}-\frac{{\rm{ \mathsf{ π} }}}{2}-\theta_{0}\right)$

(8)

同理，回流线电流和钢轨电流单独作用时在接地回路中产生的磁场分布如图 4(b)、4(c)所示。回流线单独作用时在接地回路中产生的感应电流为I_gy2，钢轨单独作用时产生的感应电流为I_gy3，其相量形式分别为

$\left\{\begin{array}{l} \boldsymbol{I}_{\mathrm{gy} 2}=\frac{\mu_{0} \omega I_{2} l}{2 {\rm{ \mathsf{ π} }} Z_{0}} \ln \frac{x_{4}}{x_{3}} \angle\left(\theta_{2}-\frac{{\rm{ \mathsf{ π} }}}{2}-\theta_{0}\right) \\ \boldsymbol{I}_{\mathrm{gy} 3}=\frac{\mu_{0} \omega I_{3} l}{2 {\rm{ \mathsf{ π} }} Z_{0}} \ln \frac{x_{6}}{x_{5}} \angle\left(\theta_{3}-\frac{{\rm{ \mathsf{ π} }}}{2}-\theta_{0}\right) \end{array}\right.$

(9)

式中：I₂和θ₂分别为回流线电流有效值和初相位；I₃和θ₃分别为钢轨电流有效值和初相位；x₃为列车车体底部与回流线间垂直距离；x₄为轮对与回流线的垂直距离；x₅为钢轨等效半径；x₆为车体底部与轮对的垂直距离。

接触线电流、回流线电流和钢轨电流在接地回路中产生的磁感应强度方向分别为顺时针、逆时针和顺时针，如图 4所示。若规定感应电流顺时针方向为正，由于感应电流方向与磁感应强度方向需满足右手螺旋关系，则接触线电流单独作用时在接地回路产生的感应电流为正，回流线产生的为负，钢轨产生的为正。依据叠加原理，整个牵引网在接地回路中产生的感应电流I_gy的相量表达式为

$\begin{aligned} \boldsymbol{I}_{\mathrm{gy}}=& \frac{\mu_{0} \omega l}{2 {\rm{ \mathsf{ π} }} Z_{0}} \ln \frac{x_{2}}{x_{1}} I_{1} \angle\left(\theta_{1}-\theta_{0}-\frac{{\rm{ \mathsf{ π} }}}{2}\right)-\\ & \frac{\mu_{0} \omega l}{2 {\rm{ \mathsf{ π} }} Z_{0}} \ln \frac{x_{4}}{x_{3}} I_{2} \angle\left(\theta_{2}-\theta_{0}-\frac{{\rm{ \mathsf{ π} }}}{2}\right)+\\ & \frac{\mu_{0} \omega l}{2 {\rm{ \mathsf{ π} }} Z_{0}} \ln \frac{x_{6}}{x_{5}} I_{3} \angle\left(\theta_{3}-\theta_{0}-\frac{{\rm{ \mathsf{ π} }}}{2}\right) \end{aligned}$

(10)

1.3 传导电流和感应电流相位关系

车体回流等于接地回路中传导电流和感应电流的矢量叠加。通过分析传导电流与感应电流两者间的相位关系，可得到考虑车–网系统间感性耦合会抬升还是抑制车体回流的关键结论。

定义图 3钢轨阻抗Z_G45相量形式为

$\boldsymbol{Z}_{\mathrm{G} 45}=R_{\mathrm{G}}+\mathrm{j} \omega L_{\mathrm{G}}=Z_{\mathrm{G} 45} \angle \theta_{4}$

(11)

联立式(1)、(7)、(11)，可求出传导电流I_cd的相量形式为

$\boldsymbol{I}_{\mathrm{cd}}=\frac{Z_{\mathrm{G} 45}}{Z_{0}} \boldsymbol{I}_{\mathrm{R}}=\frac{Z_{\mathrm{G} 45}}{Z_{0}} I_{3} \angle\left(\theta_{3}+\theta_{4}-\theta_{0}\right)$

(12)

牵引网在接地回路中产生的感应电流I_gy相量表达式如式(10)所示。由于接触线电流、钢轨电流和回流线电流处在一个闭合回路中，若忽略钢轨对地泄漏导纳，近似有θ₁=θ₂=θ₃。则感应电流I_gy相量表达式化简结果如式(13)所示。

在接触线电流、回流线电流和钢轨电流的参考方向如图 4所示的条件下，接地回路中传导电流的正方向为逆时针，感应电流正方向为顺时针。联立式(12)、(13)得到接地回路的总电流（简称车体回流）如式(14)所示。

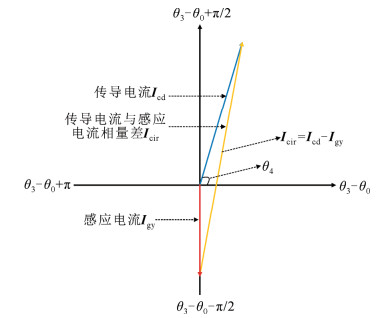
车体传导电流和感应电流的相位关系如图 5所示。由式(12)、(13)可得，感应电流相位总是滞后于车体传导电流相位θ₄ + π/2，由于钢轨阻抗相位角为0≤θ₄≤90°，使得车体传导电流相量与感应电流相量之间的夹角为钝角。根据数学上的余弦定理可得，车体回流I_cir有效值会大于车体传导电流I_cd有效值，即考虑感性耦合会起到抬升车体回流的作用。同时，车体电位等于车体回流与阻抗的乘积，故考虑感性耦合对车体电位也是抬升的作用。

图 5 车体传导电流和感应电流间相位关系

Figure 5. Phase relationship between train body conduction current and induced current

下载: 全尺寸图片幻灯片

上文以直供带回流线供电方式为例推导出考虑车–网间感性耦合会抬升车体回流大小，但同理可得出其它供电方式下感性耦合对车体回流和车体电位也是抬升作用，只是抬升幅度不同。

$\begin{aligned} &\boldsymbol{I}_{\mathrm{gy}}=\frac{\mu_{0} \omega l}{2 {\rm{ \mathsf{ π} }} Z_{0}}\left(I_{1} \ln \frac{x_{2}}{x_{1}}-I_{2} \ln \frac{x_{4}}{x_{3}}+I_{3} \ln \frac{x_{6}}{x_{5}}\right) \angle\left(\theta_{3}-\theta_{0}-\frac{{\rm{ \mathsf{ π} }}}{2}\right)= \\ &\frac{\mu_{0} \omega l}{2 {\rm{ \mathsf{ π} }} Z_{0}}\left(I_{1} \ln \frac{x_{2}}{x_{1}}-I_{2} \ln \frac{x_{4}}{x_{3}}+I_{3} \ln \frac{x_{6}}{x_{5}}\right) \angle\left(\theta_{3}+\theta_{4}-\theta_{0}-\left(\theta_{4}+\frac{{\rm{ \mathsf{ π} }}}{2}\right)\right) \end{aligned}$

(13)

$\begin{aligned} \boldsymbol{I}_{\mathrm{cir}} &=\boldsymbol{I}_{\mathrm{cd}}-\boldsymbol{I}_{\mathrm{gy}}=\frac{Z_{\mathrm{G} 45}}{Z_{0}} I_{3} \angle\left(\theta_{3}+\theta_{4}-\theta_{0}\right)-\\ & \frac{\mu_{0} \omega l}{2 {\rm{ \mathsf{ π} }} Z_{0}}\left(I_{1} \ln \frac{x_{2}}{x_{1}}-I_{2} \ln \frac{x_{4}}{x_{3}}+I_{3} \ln \frac{x_{6}}{x_{5}}\right) \\ & \angle\left(\theta_{3}+\theta_{4}-\theta_{0}-\left(\theta_{4}+\frac{{\rm{ \mathsf{ π} }}}{2}\right)\right) \end{aligned}$

(14)

2. 车–网–地耦合系统建模仿真

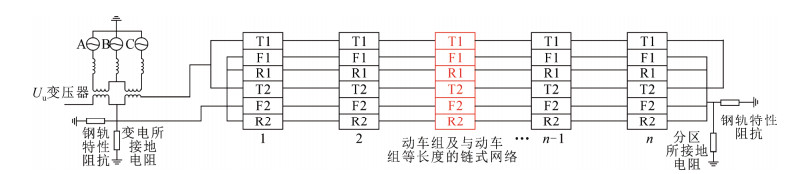
牵引网发生T–R短路时，车、网、地系统间在电气上是相互作用的。车与网间电气关系为：钢轨电流经保护接地流入车体，同时牵引网在列车接地回路中产生感应电流；车、网与地之间的电气关系为：部分钢轨电流经泄漏电阻流入大地中，产生钢轨电位，钢轨电位再经保护接地耦合至车体上。基于系统间的电气作用关系，搭建的车–网–地耦合模型如图 6所示。其中，牵引网系统采用等效π型链式电路表示，链式电路的建模方法及参数计算参考文献[24]；列车系统由车体和保护接地两部分构成，且车体通过保护接地与钢轨并联；车与网系统间的感性耦合采用受控源表示。鉴于未设置保护接地的车轴其车体对钢轨阻抗极大，故以设置保护接地的车轴所在位置和车体相邻连接处位置为分界面，将车体和牵引网链式电路模型进行分段，分段结果如图 6所示。由于牵引网发生短路时列车有可能运行在该线路任意位置，故需搭建整条线路的车–网–所模型，如图 7所示。图 7中红颜色标注的模块为图 6整体模型的封装，改变红颜色模块位置表示列车位于线路不同位置处。在变电所和分区所处并联钢轨特性阻抗来表示钢轨的无限延伸特性，同时牵引网链式电路考虑了导体间的互电感、互电容和钢轨对地泄漏电阻(在等效π型链式电路中增加钢轨对地电阻来表示网与地之间的耦合，但未在图 7中展示出来)。基于此方法建立的模型不仅与实际线路中车–网电气连接结构更相近，亦方便下文进行车体电位和车体回流影响因素仿真分析。

图 6 车–网–地耦合模型

Figure 6. Train-network-groundcoupling model

下载: 全尺寸图片幻灯片

图 7 车–网–所等效模型

Figure 7. Train-network-substation equivalent model

下载: 全尺寸图片幻灯片

图 6所示车–网–地耦合模型中，列车车体参数采用文献[6]中实测数据，参数如表 1所示，车厢间连接线等效电阻为1 mΩ。图 7所示车–网–所模型中，外部电源和牵引变压器参数如表 2所示，牵引网导体参数及空间位置如表 3所示。根据文献[24-25]可得出牵引网链式模型中各元件的参数。

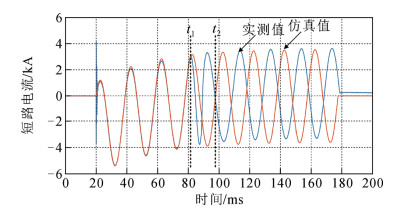
表 1 列车车体参数

Table 1. Train body parameters

车厢	01车	02车	03车	04车	05车	06车	07车	08车
阻抗/mΩ	3.4	1	1.2	1	1	1.2	1	3.4

下载: 导出CSV

| 显示表格

表 2 外部电源和牵引变压器参数

Table 2. External power supply and traction transformer parameters

系统组件	参数名称	参数取值
外部电源110 kV	容量/MVA	3000
外部电源110 kV	正序阻抗/Ω	4.03
牵引变压器	变压器接线方式	Vv接线
	变压器变比	110/27.5
	变压器容量/MVA	31.5
	电压百分比/%	10.5

下载: 导出CSV

| 显示表格

表 3 牵引网导体参数及空间位置

Table 3. Tractionnetwork conductor parameters and spatial position

导体	型号	直流电阻/(Ω·km^–1)	等效半径/cm	水平垂直坐标/cm	导体	型号	直流电阻/(Ω·km^–1)	等效半径/cm	水平垂直坐标/cm
接触线1	CTS–150	0.159	0.72	(0, 645)	接触线2	CTS–150	0.159	0.72	(460, 645)
承力索1	JTMH–120	0.242	0.7	(0, 785)	承力索2	JTMH–120	0.242	0.7	(460, 785)
钢轨1	P60	0.135	1.279	(–71.75, 0)	钢轨3	P60	0.135	1.279	(388.25, 0)
钢轨2	P60	0.135	1.279	(71.75, 0)	钢轨4	P60	0.135	1.279	(531.75, 0)
回流线1	LBGLJ–185/25	0.145	0.945	(–340, 780)	回流线2	LBGLJ–185/25	0.145	0.945	(800, 780)

下载: 导出CSV

| 显示表格

为验证车–网间感性耦合对车体电位和车体回流有抬升作用，分别对考虑感性耦合和不考虑感性耦合下的车体电位和车体回流进行仿真求解，并与实测对比。由于短路电流是产生车体电位的激励源，在保证实测与仿真中激励源一致的前提下，才能去对比是否考虑感性耦合情况下车体电位的仿真值与实测值之间的误差。实测数据为车体对轴端电位差波形(该车轴设置了保护接地)，故选取4号车车体对轴端电位差的仿真结果进行对比。短路电流的仿真结果与实测结果如图 8所示。由图 8可看出，在t₁时刻之前，短路电流仿真波形和实测波形有较好的一致性；而在t₁时刻和t₂时刻之间，短路电流实测波形出现了频率的突变(可能由于实际试验时出现电弧所致)，使得仿真波形与实测波形反相，但幅值基本保持一致。依据文献[26]可知，该型列车地板面至轨道表面距离为125 cm，列车接地回路长度为10 m，通过理论计算，短路时牵引网在列车接地回路中产生的感应电压有效值为8.89 V，相位为–155.4°，车体对轴端电位差的仿真结果和实测结果如图 9所示。

图 8 短路电流实测与仿真结果对比

Figure 8. Comparison of short-circuit current measurement and simulation results

下载: 全尺寸图片幻灯片

图 9 车体对轴端电位差实测与仿真结果对比

Figure 9. Comparison of actual measurement and simulation results of potential difference between train body and wheel

下载: 全尺寸图片幻灯片

由图 9可知：与实测结果相比，考虑感性耦合时，车体对轴端电位差的周期分量有效值与实测值相差1.04 V，误差为8.9%；而不考虑感性耦合时，车体对轴端电位差的周期分量有效值与实测值相差6.30 V，误差为54.0%。综上，可表明考虑车–网间感性耦合不仅对车体电位有抬升作用，而且计算结果与实际值更相符。因此，下文利用考虑了感性耦合的车–网–地模型，仿真分析车体电位和车体回流的分布大小及影响因素，以期得到更准确的结果。

3. 车体电位及车体电流影响因素分析

由上文理论分析知车体回流等于列车接地回路中传导电流和感应电流的矢量叠加，而流入接地回路中的传导电流与钢轨电流及车体对轴端等效阻抗有关，感应电流与牵引网各导体电流及列车位置有关，同时车体对地电位还受钢轨对地泄漏电阻的影响。因此，利用搭建的模型仿真分析短路点位置、列车位置、车体对轴端等效阻抗和钢轨泄漏电阻对车体电位和车体回流分布大小的影响。

3.1 车体对轴端等效阻抗的影响

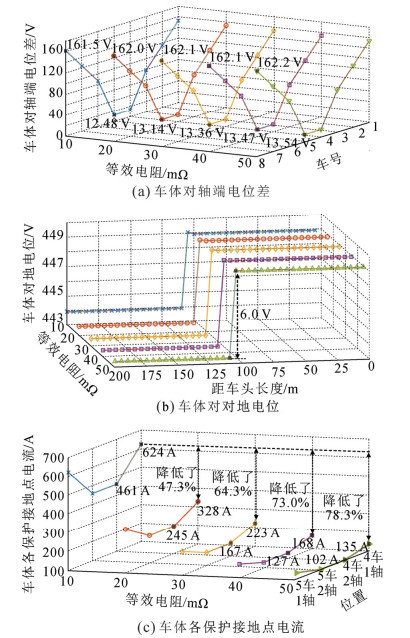
TB/T 2977—2016《铁道车辆金属部件的接地保护》中规定列车车体与轨道间的等效电阻≤50 mΩ。因此在仿真中设置车体对轴端的等效电阻分别为10、20、30、40和50 mΩ，分析等效电阻变化对车体电位和车体回流的影响。仿真其它条件为：短路点位于距变电所2 km处(模拟变电所近端短路对列车接地系统的冲击，短路方式均为T–R金属性短路)，列车位于短路点附近且在钢轨主回流侧，钢轨对地泄漏电阻为2 Ω/km。2 km短路时牵引网在列车接地回路中产生的感应电压有效值为14.81 V，相位为–176.31°。车体电位和车体回流仿真结果见图 10。

图 10 车体对轴端等效电阻对车体电位和车体回流的影响

Figure 10. Effect of train body-to-axle equivalent resistance on train body potential and body return current

下载: 全尺寸图片幻灯片

距变电所2 km处短路时，短路电流为7 499 A。由图 10(a)可看出，车体对轴端电位差呈现出端车大、中间车小的分布规律；同时在车体不同位置间出现电位差(因为在4车1轴和5车1轴间存在接地回路)，电位差最大达到6 V，如图 10(b)所示。车体对轴端等效电阻由10 mΩ增大至50 mΩ时，端车车体对轴端的电位差增加了0.7 V，中间车车体对轴端的电位差增加了0.4 V，故增大等效电阻对车体电位基本不影响，但能显著降低车体回流的大小。车体回流等于4车1轴和4车2轴电流之和(也等于5车1轴和5车2轴电流之和)，等效电阻由10 mΩ增大到50 mΩ时，车体回流由1 085 A降低至237 A，降低了78.3%。同时流经各保护接地点的电流如图 10(c)所示，各保护接地点间电流分配不均匀：等效电阻为10 mΩ时，4车1轴与4车2轴间电流相差163 A；等效电阻为50 mΩ时，4车1轴与4车2轴间电流相差34 A。

3.2 短路点位置的影响

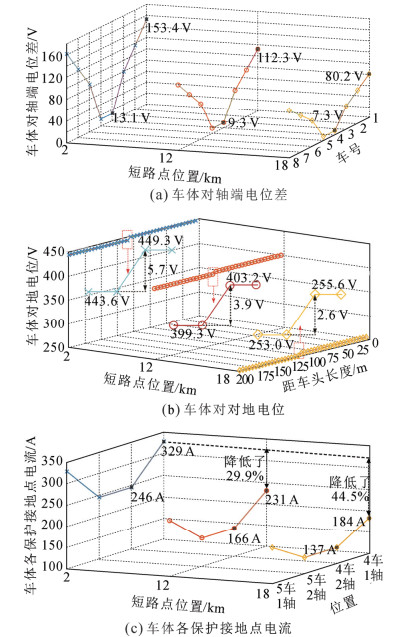
短路电流大小随短路点位置而变化，在仿真中设置短路点分别位于距变电所2、12和18 km处，分析在变电所近端、中间和末端短路时车体电位和车体回流的分布大小。仿真其它条件为：车体对轴端等效电阻为20 mΩ，列车位于短路点附近且在钢轨主回流侧，钢轨对地泄漏电阻为2 Ω/km。2 km短路时牵引网在列车接地回路中产生的感应电压为14.81 V，相位为–176.31°；12 km短路时牵引网在列车接地回路中产生的感应电压为8.89 V，相位为–169.36°；18 km短路时牵引网在列车接地回路中产生的感应电压为7.80 V，相位为–168.14°。车体电位和车体回流仿真结果如图 11所示。

图 11 短路点位置对车体电位和车体回流的影响

Figure 11. Influence of the position of short-circuit point on train body potential and body return current

下载: 全尺寸图片幻灯片

距变电所2、12和18 km短路时，短路电流分别为7 499 A、4 505 A和3 945 A。由图 11可看出，短路电流越大，产生的车体电位和车体回流越大。其中，2 km短路时，头车车体与轴端间的电位差达到153.4 V，中间车达到13.1 V；12 km短路时，头车车体与轴端间电位差为112.3 V，中间车为9.3 V；18 km处短路时，头车车体与轴端间电位差为80.2 V，中间车为7.3 V。分别在2、12和18 km短路时，车体不同位置间的电位差最高为5.7、3.9和2.6 V，车体回流分别为574、397和321 A。流过各保护接地点的电流如图 11(c)所示，2 km短路时，4车1轴与4车2轴间电流相差83 A；12 km短路时两者间相差65 A，18 km短路时两者间相差46 A。

3.3 列车位置的影响

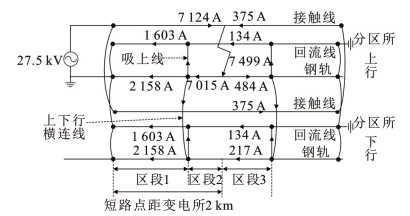
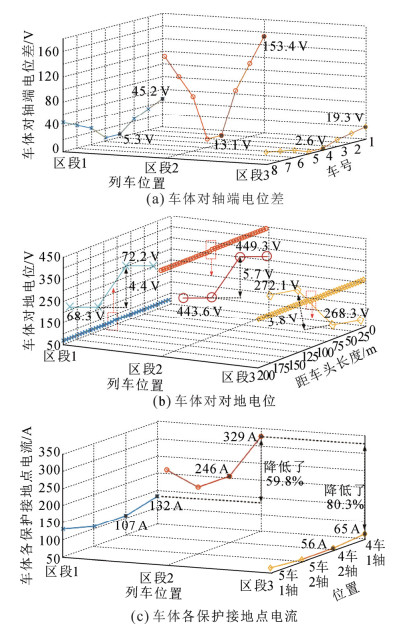
对于直供带回流线的供电方式，列车总是位于两根吸上线之间。在距变电所2 km处短路时，牵引网各导体电流的分布大小如图 12所示。假设将变电所处的吸上线与短路点左侧最近的吸上线间的距离称为区段1，短路点左侧最近的吸上线与短路点间的距离称为区段2，短路点与短路点右侧最近的吸上线间的距离称为区段3。由于区段1、区段2和区段3上各导体电流大小不同，使得列车位于不同区段时接地回路中的传导电流和感应电流将不同。分析改变列车位置对车体电位和车体回流的影响，仿真其它条件为：短路点位于距变电所2 km处，车体对轴端等效电阻为20 mΩ，钢轨对地泄漏电阻为2 Ω/km。当列车分别位于区段1、区段2和区段3时，牵引网在列车接地回路中产生的感应电压为6.99、14.81和3.97 V，相位均为–176.31°。车体电位和车体回流仿真结果如图 13所示。

图 12 距变电所2 km短路时各导体电流分布大小

Figure 12. Current distribution of each conductor when a short circuit is 2 km away from the substation

下载: 全尺寸图片幻灯片

图 13 列车位置对车体电位和车体回流的影响

Figure 13. Effect of train position on train body potential and body return current

下载: 全尺寸图片幻灯片

由图 13可看出，列车位于区段2时，车体电位和车体电流均最大。当列车位置从区段2更换到区段1时，端车车体与轴端间的电位差从153.4 V变为45.2 V，降低了108.2 V；中间车车体与轴端间的电位差从13.1 V变为5.3 V，降低了7.8 V；车体不同位置间的电位差由5.7 V降低到4.4 V；车体回流由574 A降低到239 A，降低了58.3%。当列车位置从区段2更换到区段3时，端车车体与轴端间的电位差从153.4 V变为19.3 V，降低了134.1 V；中间车车体与轴端间的电位差从13.1 V变为2.6 V，降低了10.5 V；车体不同位置间的电位差由5.7 V降低到3.8 V；车体回流由574 A降低到121 A，降低了78.9%。可见，当列车位于区段2时，短路电流对列车接地系统的冲击最大，区段1次之，区段3最小。

3.4 钢轨对地泄漏电阻的影响

分析钢轨对地电阻分别为2、20和50 Ω/km时车体电位和车体回流的分布大小。仿真其它条件为：短路点位于距变电所2 km处，列车位于短路点附近且在钢轨主回流侧，车体对轴端等效电阻为20 mΩ。2 km短路时牵引网在列车接地回路中产生的感应电压为14.81 V，相位为–176.31°。车体电位和车体回流仿真结果如图 14所示。

图 14 钢轨泄漏电阻对车体电位和车体回流的影响

Figure 14. Influence of rail leakage resistance on train body potential and body return current

下载: 全尺寸图片幻灯片

由图 14可看出，钢轨对地泄漏电阻从2 Ω/km增大到50 Ω/km时，端车车体与轴端间的电位差从153.4 V增大到179.7 V，增加了26.3 V；中间车车体与轴端间的电位差从13.1 V增大到15.2 V，增加了2.1 V；车体不同位置间的电位差由5.7 V增大到13.9 V，车体对地电位由449.3 V增大到635.9 V；同时，车体回流由574 A增大到657 A，增幅为14.5%。因此，改变钢轨对地泄漏电阻对车体与轴端间电位差和车体回流均影响较小，但对车体对地电位影响较大。上文在对车体回流理论推导时，为方便计算作了忽略钢轨泄漏电阻的假设，而由仿真结果可知改变泄漏电阻大小对车体回流影响较小，表明理论推导中假设的合理性。

4. 结论

1）车体回流等于列车接地回路中传导电流和感应电流的矢量叠加，依据牵引供电系统分析和电磁场理论，推导出接地回路中传导电流和感应电压的相量表达式，通过两者间的相位关系得出了考虑车–网间感性耦合会抬升车体电位和车体回流的重要结论。

2）分别对考虑和不考虑感性耦合下的车体电位进行仿真求解，并与实测数据对比，表明理论推导的正确性及仿真模型的准确性。

3）基于仿真模型进行短路故障下车体电位和车体回流影响因素的研究，得出：车体对轴端电位差主要受短路点位置和列车位置的影响，车体对地电位主要受钢轨对地泄漏电阻的影响，车体回流主要受车体对轴端等效电阻影响。

图 1 某列车接地系统方式

Figure 1. A train grounding system method

下载: 全尺寸图片幻灯片

图 2 车–网系统间电气耦合关系

Figure 2. Electrical coupling relationship between train-network systems

下载: 全尺寸图片幻灯片

图 3 列车接地回路等效模型

Figure 3. Equivalent model of train ground loop

下载: 全尺寸图片幻灯片

图 4 牵引网各导线作用下的接地回路磁场分布

Figure 4. Distribution of magnetic field in ground loop under the action of conductors in traction network

下载: 全尺寸图片幻灯片

图 5 车体传导电流和感应电流间相位关系

Figure 5. Phase relationship between train body conduction current and induced current

下载: 全尺寸图片幻灯片

图 6 车–网–地耦合模型

Figure 6. Train-network-groundcoupling model

下载: 全尺寸图片幻灯片

图 7 车–网–所等效模型

Figure 7. Train-network-substation equivalent model

下载: 全尺寸图片幻灯片

图 8 短路电流实测与仿真结果对比

Figure 8. Comparison of short-circuit current measurement and simulation results

下载: 全尺寸图片幻灯片

图 9 车体对轴端电位差实测与仿真结果对比

Figure 9. Comparison of actual measurement and simulation results of potential difference between train body and wheel

下载: 全尺寸图片幻灯片

图 10 车体对轴端等效电阻对车体电位和车体回流的影响

Figure 10. Effect of train body-to-axle equivalent resistance on train body potential and body return current

下载: 全尺寸图片幻灯片

图 11 短路点位置对车体电位和车体回流的影响

Figure 11. Influence of the position of short-circuit point on train body potential and body return current

下载: 全尺寸图片幻灯片

图 12 距变电所2 km短路时各导体电流分布大小

Figure 12. Current distribution of each conductor when a short circuit is 2 km away from the substation

下载: 全尺寸图片幻灯片

图 13 列车位置对车体电位和车体回流的影响

Figure 13. Effect of train position on train body potential and body return current

下载: 全尺寸图片幻灯片

图 14 钢轨泄漏电阻对车体电位和车体回流的影响

Figure 14. Influence of rail leakage resistance on train body potential and body return current

下载: 全尺寸图片幻灯片

表 1 列车车体参数

Table 1 Train body parameters

车厢	01车	02车	03车	04车	05车	06车	07车	08车
阻抗/mΩ	3.4	1	1.2	1	1	1.2	1	3.4

下载: 导出CSV

表 2 外部电源和牵引变压器参数

Table 2 External power supply and traction transformer parameters

系统组件	参数名称	参数取值
外部电源110 kV	容量/MVA	3000
外部电源110 kV	正序阻抗/Ω	4.03
牵引变压器	变压器接线方式	Vv接线
	变压器变比	110/27.5
	变压器容量/MVA	31.5
	电压百分比/%	10.5

下载: 导出CSV

表 3 牵引网导体参数及空间位置

Table 3 Tractionnetwork conductor parameters and spatial position

导体	型号	直流电阻/(Ω·km^–1)	等效半径/cm	水平垂直坐标/cm	导体	型号	直流电阻/(Ω·km^–1)	等效半径/cm	水平垂直坐标/cm
接触线1	CTS–150	0.159	0.72	(0, 645)	接触线2	CTS–150	0.159	0.72	(460, 645)
承力索1	JTMH–120	0.242	0.7	(0, 785)	承力索2	JTMH–120	0.242	0.7	(460, 785)
钢轨1	P60	0.135	1.279	(–71.75, 0)	钢轨3	P60	0.135	1.279	(388.25, 0)
钢轨2	P60	0.135	1.279	(71.75, 0)	钢轨4	P60	0.135	1.279	(531.75, 0)
回流线1	LBGLJ–185/25	0.145	0.945	(–340, 780)	回流线2	LBGLJ–185/25	0.145	0.945	(800, 780)

下载: 导出CSV

参考文献(26)

[1]	王辉, 李群湛, 解绍锋, 等. 采用YNd-SVG的电气化铁路负序补偿模型及控制策略[J]. 高电压技术, 2021, 47(5): 1740-1750. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwQ9V3KaAo_eXc%2BOcUsSBLJ0%3D?encrypt=1 WANG Hui, LI Qunzhan, XIE Shaofeng, et al. Negative sequence compensation model and control strategy of electrified railway with YNd tansformer and SVG[J]. High Voltage Engineering, 2021, 47(5): 1740-1750. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwQ9V3KaAo_eXc%2BOcUsSBLJ0%3D?encrypt=1
[2]	张宇, 王辉, 李群湛, 等. 基于Dd匹配变和SVG的牵引变电所群贯通供电系统负序治理方案及控制策略[J]. 高电压技术, 2021, 47(1): 150-158. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwcaSfniPTs%2BoZHjg1qiuz5I%3D?encrypt=1 ZHANG Yu, WANG Hui, LI Qunzhan, et al. Negative sequence treatment and control strategy for the co-phase interconnected power supply system of traction substation group based on Dd transformer and SVG[J]. High Voltage Engineering, 2021, 47(1): 150-158. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwcaSfniPTs%2BoZHjg1qiuz5I%3D?encrypt=1
[3]	吴广宁, 李晓楠, 杨雁, 等. 车载变压器故障预测与健康管理研究进展[J]. 高电压技术, 2020, 46(3): 876-889. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwd0n6B_yyB3mGsKEgKDxLM4%3D?encrypt=1 WU Guangning, LI Xiaonan, YANG Yan, et al. Research progress of fault prediction and health management for on-board traction transformers[J]. High Voltage Engineering, 2020, 46(3): 876-889. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwd0n6B_yyB3mGsKEgKDxLM4%3D?encrypt=1
[4]	中国人民共和国铁道部. 铁道车辆金属部件的接地保护: TB/T 2977—2016[S]. 北京: 中国铁道出版社, 2016. Ministry of Railways of the People's Republic of China. Ground protection of the metal parts of railway vehicle: TB/T 2977—2016[S]. Beijing, China: China Railway Publishing House, 2016.
[5]	高国强. 高速列车运行状态暂态过电压机理与抑制方法的研究[D]. 成都: 西南交通大学, 2012. GAO Guoqiang. Study on the over-voltage mechanism and suppressing method for high-speed train[D]. Chengdu, China: Southwest Jiaotong University, 2012.
[6]	李石. 动车组保护接地方案研究[D]. 北京: 北京交通大学, 2013. LI Shi. Research on the protective grounding scheme of electric multiple units[D]. Beijing, China: Beijing Jiaotong University, 2013.
[7]	张维国. 客车车体转向架电气接地问题探讨[J]. 铁道车辆, 2000, 38(11): 21-23. DOI: 10.3969/j.issn.1002-7602.2000.11.008 ZHANG Weiguo. Discussion of electrical grounding of carbody and bogie of passenger car[J]. Rolling Stock, 2000, 38(11): 21-23. DOI: 10.3969/j.issn.1002-7602.2000.11.008
[8]	郭晖. 车辆的接地电流[J]. 国外铁道车辆, 2001, 38(6): 39-45. https://www.cnki.com.cn/Article/CJFDTOTAL-GWTD200106011.htm GUO Hui. Grounding current of cars[J]. Foreign Rolling Stock, 2001, 38(6): 39-45. https://www.cnki.com.cn/Article/CJFDTOTAL-GWTD200106011.htm
[9]	MULERTT C. Toprevent electric current through the bearings[J]. Foreign Rolling Stock, 1994, 12(3): 46-49.
[10]	牛可可. 车体地电流的研究[D]. 北京: 北京交通大学, 2016. NIU Keke. Research on grounding current of trains[D]. Beijing, China: Beijing Jiaotong University, 2016.
[11]	刘耀银. 高速动车组接地方式对接地回流分布的影响研究[D]. 成都: 西南交通大学, 2017. LIU Yaoyin. Study on the effect of grounding methods of high-speed EMU on distribution of grounding return current[D]. Chengdu, China: Southwest Jiaotong University, 2017.
[12]	魏晓斌, 高国强, 陈盼, 等. 保护接地对高速动车组接地回流的影响[J]. 铁道学报, 2017, 39(8): 39-44. WEI Xiaobin, GAO Guoqiang, CHEN Pan, et al. Influence of protective grounding on high-speed EMU grounding reflux[J]. Journal of the China Railway Society, 2017, 39(8): 39-44.
[13]	黄可, 刘志刚, 王英, 等. 动车组过分相的车体最佳接地技术分析[J]. 电力系统及其自动化学报, 2016, 28(5): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-DLZD201605001.htm HUANG Ke, LIU Zhigang, WANG Ying, et al. Analysis of optimal body grounding technology in case of electric multiple unit passing neutral section device[J]. Proceedings of the CSU-EPSA, 2016, 28(5): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-DLZD201605001.htm
[14]	高国强, 刘耀银, 万玉苏, 等. 高速动车组升弓浪涌过电压研究[J]. 高电压技术, 2016, 42(9): 2909-2915. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwac7SJ8a1yXBIZfOKR5h2oI%3D?encrypt=1 GAO Guoqiang, LIU Yaoyin, WAN Yusu, et al. Study of surge overvoltage when rising pantograph for high-speed electric multiple unit[J]. High Voltage Engineering, 2016, 42(9): 2909-2915. http://hve.epri.sgcc.com.cn/x_iA9ig181GiGW7b5ocZwac7SJ8a1yXBIZfOKR5h2oI%3D?encrypt=1
[15]	HATSUKADE S, MAEDA T. Experiment and basic analysis of surges on a rolling stock's body[J]. IEEJ Transactions on Power and Energy, 2005, 125(8): 754-758. DOI: 10.1541/ieejpes.125.754
[16]	HATSUKADE S. Reduction method of surge voltage on AC railcar's body[J]. Quarterly Report of RTRI, 2009, 50(2): 70-75. DOI: 10.2219/rtriqr.50.70
[17]	李朋真. 动车组车体过电压及其对轴端速度传感器的电磁干扰分析[D]. 成都: 西南交通大学, 2017. LI Pengzhen. The overvoltage of EMU and its electromagnetic interference to the shaft end speed sensor[D]. Chengdu, China: Southwest Jiaotong University, 2017.
[18]	曹保江, 宋勇葆, 魏文赋, 等. 高速动车组雷电波侵入特性及传播规律研究[J]. 铁道学报, 2019, 41(12): 26-33. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201912004.htm CAO Baojiang, SONG Yongbao, WEI Wenfu, et al. Study on intrusion and propagation characteristics of lightning overvoltage in high-speed electric multiple unit[J]. Journal of the China Railway Society, 2019, 41(12): 26-33. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201912004.htm
[19]	刘东来. 高速动车组接地技术研究[D]. 成都: 西南交通大学, 2013. LIU Donglai. Study on grounding technology of high-speed trains[D]. Chengdu, China: Southwest Jiaotong University, 2013.
[20]	冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000. FENG Cizhang, MA Xikui. An introduction to engineering electromagnetic fields[M]. Beijing, China: Higher Education Press, 2000.
[21]	董昭德, 马庆安, 郭凯. 铁路牵引网短路瞬间的工频磁场仿真分析[C]∥中国铁道学会电气化委员会2017年年会及新技术研讨会论文集. 保定: 中国铁道学会, 2017: 143-145. DONG Zhaode, MA Qing'an, GUO Kai. Simulation analysis of power frequency magnetic field at the moment of short circuit of railway traction network[C]∥Baoding, China: China Railway Society, 2017: 143-145.
[22]	钱澄浩, 何正友, 高朝晖, 等. 高速铁路全并联AT牵引网短路故障情况下磁场环境特性分析[J]. 电力自动化设备, 2014, 34(3): 155-161. https://www.cnki.com.cn/Article/CJFDTOTAL-DLZS201403026.htm QIAN Chenghao, HE Zhengyou, GAO Chaohui, et al. Analysis of magnetic environment characteristics for high-speed railway all-parallel AT traction network with short circuit[J]. Electric Power Automation Equipment, 2014, 34(3): 155-161. https://www.cnki.com.cn/Article/CJFDTOTAL-DLZS201403026.htm
[23]	成业, 刘志刚, 黄可, 等. 基于ATP-EMTP的牵引网回路对动车组车体接地回路电气耦合作用研究[J]. 铁道学报, 2018, 40(4): 43-51. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201804007.htm CHENG Ye, LIU Zhigang, HUANG Ke, et al. Study on electrical coupling effect of traction network loop circuit on vehicle body earth loop circuit of electric multiple unit based on ATP-EMTP[J]. Journal of the China Railway Society, 2018, 40(4): 43-51. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201804007.htm
[24]	吴命利. 电气化铁道牵引网的统一链式电路模型[J]. 中国电机工程学报, 2010, 30(28): 52-58. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201028010.htm WU Mingli. Uniform chain circuit model for traction networks of electric railways[J]. Proceedings of the CSEE, 2010, 30(28): 52-58. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201028010.htm
[25]	李群湛, 贺建闽. 牵引供电系统分析[M]. 成都: 西南交通大学出版社, 2007. LI Qunzhan, HE Jianmin. Analysis of traction power supply system[M]. Chengdu, China: Southwest Jiaotong University Press, 2007.
[26]	张曙光. CRH5型动车组[M]. 北京: 中国铁道出版社, 2008. ZHANG Shuguang. CRH5 EMU[M]. Beijing, China: China Railway Press, 2008.