0.   引言

《“十四五”可再生能源发展规划》大力推动了可再生能源大规模、高比例、市场化、高质量发展^[1]。如今，我国高比例新能源并网已成为趋势，风、光资源丰富的西北地区，新能源发电占比达到50%，部分省份甚至达到70%^[2]，但随着新能源装机占比逐年提高，新能源的随机性与波动性对电力实时供需平衡的冲击越来越大^[3]。目前传统的调峰、调频、备用等辅助服务难以满足系统灵活性需求^[4]，急需一些新型灵活调节产品来应对新能源出力不稳定导致电网频繁波动的问题。近年来，爬坡辅助服务作为一种新型辅助服务品种，凭借其灵活性与价格优势成为研究热点对象，其本质为在当前交易时段，对中标发电机组预留部分发电容量，来应对下一交易时段系统爬坡能力不足的情况，其价格普遍采用机会成本定价^[5]。目前，爬坡辅助服务市场参与主体一般仅为火电机组，没有考虑储能等新型主体^[6]；而且对火电机组产生的机会成本计算模糊，容易在主能量与爬坡市场获取双重收益，从而补偿容量远大于产生机会成本对应的容量，过度补偿问题导致系统运行成本增加。因此，亟待研究加入储能后，多主体参与电能量与爬坡辅助服务市场的精细化联合出清方法。

建立完善的爬坡辅助服务市场机制能够有效增加系统运行的灵活性，增强抗干扰能力，降低运营成本。近年来，由美国的加州电力市场^[7]率先提出灵活性爬坡产品(flexible ramping product，FRP)，以应对未来5min调度区间内净负荷的波动与不确定性^[5]。文献[8]提出一种爬坡容量校验机制，通过“添加约束-反复校验”的方式建立了电能量-爬坡辅助服务联合出清模型，但增加了求解时间，牺牲了计算效率。文献[9]在构建虚拟竞标曲线的基础上，建立了爬坡辅助服务两阶段实时出清模型，但其虚拟竞标曲线仅针对满发机组，其他未满发的中标机组难以适用。文献[10]考虑机组在投入/退出时与正常运行时爬坡速率有所不同，改进了爬坡速率与爬坡能力约束，建立了爬坡辅助服务与弃风惩罚电能量市场出清模型，但其补偿容量远超机会成本对应容量，系统运营成本较高。文献[11-13]对电力系统灵活调节能服务进行了综述，提出了考虑FRP的优化调度模型与市场机制。文献[14]对FRP实施的可行性进行了分析，此外还通过考虑净负荷预测及净负荷的不确定性对系统爬坡需求进行建模。文献[15]针对15min内净负荷的波动对现有FRP模型进行改进，进一步提升了系统运行的灵活性，并对提供FRP的机组进行合理补偿。文献[16]提出了一种基于交替方向乘子法(alternating direction method of multipliers，ADMM)分布式出清方法，提升了系统出清的效率。文献[17]提出了一种FRP与电能量市场联合出清的模型，能够减小峰值电价，降低系统运行成本。上述文献考虑的爬坡市场参与主体一般仅有火电机组，没有利用火电机组、储能、需求响应和弃风弃光全手段充分挖掘系统运行灵活性，此外，这些文献构建的出清模型没有充分考虑主能量与爬坡市场耦合特性，产生了机组在主能量市场没有牺牲出力却又在爬坡市场获得补偿的双重收益，即机组机会成本并没有真实发生却获得了爬坡补偿。

不少文献对于储能参与各类市场进行了研究。文献[18]基于储能申报充、放电价差的竞价策略，建立了包含独立储能的电能量市场出清模型，降低了独立储能的收益损失。文献[19-21]对储能在各个市场间的容量分配进行研究，发现在参与提供FRP的情况下，电池储能可以获得更高的利润。文献[22]根据储能灵活能量状态运行方式的特点，建立了允许储能申报能量状态需求响应曲线和充放电成本的调度模型，降低了储能的市场风险。文献[23]从电网侧储能出发，建立一种储能参与现货市场竞价的双层博弈模型。文献[24]考虑系统灵活性供需平衡，建立了年化综合成本最低为目标的长短期储能联合规划两阶段模型。文献[25]对独立储能参与现货市场与调频辅助服务市场出清机制进行研究，并提出了顺序出清和联合出清两种出清模型。上述文献均没有考虑储能同时参与主能量和爬坡辅市场，更没有考虑储能与火电机组、需求响应等灵活性资源在爬坡市场中的相互关系。

基于现有研究存在的问题，本文提出一种计入储能的电能量市场与爬坡市场联合出清方法。首先，考虑系统净负荷变化量与新能源出力预测误差确定系统爬坡需求，其次，求取不考虑爬坡容量约束的常规电力市场出清结果，确定系统自然爬坡能力，根据爬坡缺额确定是否需要开启爬坡辅助服务市场；然后，系统自然爬坡能力不足时，火电机组采用虚拟报量-虚拟报价参与爬坡市场，储能采用最大爬坡容量参与爬坡市场。在联合出清模型中引入机组出力减小量这一变量，建立电能量与爬坡市场的耦合关系，并通过Gurobi求解器进行模型求解。最后，通过某省实际运行数据，验证所提方法的正确性及经济性，同时避免了对火电机组进行双重补偿的问题。

1.   计入储能的电能量与爬坡市场联合出清基本框架

本文聚焦于大规模新能源并网下，新型电力系统波动性与不确定性增强，提出了储能参与下主能量与爬坡市场联合出清模型，实现新型电力系统经济、稳定运行。总体流程如图 1所示。

图  1  爬坡辅助服务市场机制流程图

Figure  1.  Flowchart of market mechanisms for ramping assistance services

下载: 全尺寸图片 幻灯片

具体流程分为以下3部分：

1）爬坡需求确定。

本文前提条件为已在日前市场中完成考虑安全约束的机组组合(security constrained unit commitment，SCUC)模型计算，各机组开、停机状态已确定。首先，根据负荷预测曲线与新能源预测出力曲线相减确定系统净负荷曲线，并根据相邻时段净负荷差值确定各时段确定性爬坡需求；然后，采用下一时段风光出力的最大误差描述当前时段不确定性爬坡需求。最后，二者相加即为系统爬坡需求。

2）自然爬坡能力模型。

首先，机组在一定出力状态下，下一时段能够提供的最大增出力或最大降出力即为机组当前时段的自然爬坡能力。然后，系统灵活调节能力可通过将系统所有开机机组自然爬坡能力求和得到。最后，将系统各时段灵活调节能力与爬坡需求比较可以确定各时段爬坡缺额情况。

3）计入火电、储能、需求响应与弃风弃光的电能量与爬坡联合出清模型。

爬坡市场开启后，确认开机的火电机组通过虚拟报量-报价的方式参与市场，同时储能以最大爬坡容量与固定补偿价格的方式参与市场。在此基础上构建计入火电、储能、需求响应与弃风弃光的主能量与爬坡联合出清模型。本文建立的主能量与爬坡联合出清模型本质上属于线性规划问题，可通过Gurobi求解器求解，爬坡市场出清价格采用拉格朗日乘子法求取。

2.   爬坡需求

爬坡辅助服务市场的引入是为了增强系统当前时段的爬坡能力以应对下一时段净负荷变化过大的情况。如今大规模的风电、光伏的并网，导致系统净负荷频繁发生突升/突降的情况，系统的爬坡需求增加，此时传统的现货市场出清模型无法满足系统对上、下爬坡能力的需求，因此本文在考虑通过调度手段增加火电机组爬坡能力的基础上，引入储能参与爬坡辅助服务市场，进一步增强系统运行的灵活性与经济性。

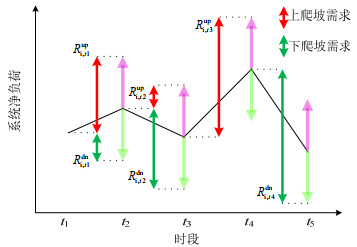
爬坡能力需求由两部分构成，一部分是确定性爬坡需求即相邻时段净负荷的变化量，另一部分是考虑新能源出力预测偏差和负荷预测偏差而预留的安全裕度^[26]，各时段系统上、下爬坡需求如图 2所示，红色(绿色)箭头为当前时段需要预留的上(下)爬坡能力，具体数值则由下一时段净负荷上(浅红色)、下(浅绿色)波动量确定。同时从图中可以看出各个时段可能仅存在上爬坡需求或仅存在下爬坡需求，也可能上、下爬坡需求都存在。

图  2  爬坡需求示意图

Figure  2.  Sketch map of ramping demand

下载: 全尺寸图片 幻灯片

爬坡需求计算公式如下所示：

式中：$R_t^{{\text{up}}}$和$R_{\text{t}}^{{\text{dn}}}$分别为系统在$t$时刻上爬坡和下爬坡需求；$P_{t + 1}^{{\text{load}}}$和$P_t^{{\text{load}}}$分别为系统在$t + 1$时刻和$t$时刻的负荷预测值；$P_{t + 1}^{\text{e}}$和$P_t^{\text{e}}$分别为新能源在$t + 1$时刻和$t$时刻的预测出力；${\omega _{t + 1}}$为新能源在$t + 1$时刻的最大预测偏差；T为出清时段总数。

3.   自然爬坡能力模型

确定系统自然爬坡能力的前提是需要确定各机组的出力计划，同时结合机组出力上下限及机组爬坡速率即可计算得出。机组出力计划通过常规电能量市场经济调度模型计算得到，通过求解模型可以确定机组的出清电量$P_{i,t}^{{{\text{G}}_{{\text{en}}}}}$及系统边际电价${\lambda _t}$。

式中：${N_{\text{F}}}$为系统火电机组总数；${C_{i,t}}$为机组$i$在$t$时刻的电能量报价；$P_{i,t}^{{{\text{G}}_{{\text{en}}}}}$为火电机组$i$在$t$时刻的出力；${N_{\text{W}}}$为新能源机组总数；$P_{j,t}^{\text{W}}$和$P_{j,t}^{{{\text{W}}_{{\text{en}}}}}$分别为新能源机组$j$在$t$时刻的预测出力与调度出力；${\alpha _1}$为弃风弃光惩罚因子。

约束条件包括：

式中：$P_t^{{\text{load}}}$为系统$t$时刻负荷需求；$P_i^{\max }$和$P_i^{{\text{min}}}$分别为机组$i$最大出力与最小出力；${\gamma _{\text{u}}}$和${\gamma _{\text{d}}}$分别为正备用、负备用系数；${R_i}$为机组$i$的爬坡速率；式(3)为系统功率平衡约束；式(4)为机组出力上下限约束；式(5)和式(6)分别为正、负备用约束；式(7)为机组爬坡、滑坡约束。本文暂不考虑系统潮流约束。

储能在文中以电化学储能为主，电池储能的运行过程包括充电和放电两个工作状态，储能约束主要包括最大充电、放电功率限制和荷电状态(state of charge，SOC)约束，相关各项约束如下：

式中：$P_{{\text{ch}},t - 1}^{{\text{en}}}$、$P_{{\text{dis}},t - 1}^{{\text{en}}}$分别为储能在$t - 1$时刻的充电功率和放电功率；${P_{{\text{ch}},\max }}$、${P_{{\text{dis}},\max }}$分别为储能的最大充电功率和最大放电功率；$S_t^{{\text{en}}}$为储能在$t$时刻的荷电状态；$S_{t - 1}^{{\text{en}}}$为储能在$t$时刻的荷电状态；$S_{\min }^{{\text{en}}}$、$S_{\max }^{{\text{en}}}$分别为储能允许荷电状态上下限；${\eta _{{\text{ch}}}}$、${\eta _{{\text{dis}}}}$分别为储能的充、放电效率；$\Delta t$表示单时段时间步长，本文取1h。

一般来说储能要求每日的荷电状态保持不变，故增加约束：

由于本文考虑的主要为电网侧储能，上述模型未考虑储能的收益，但由于目标函数为总成本最小，储能会被尽可能安排在电价低谷时段充电、电价高峰时段放电，但储能无法根据峰谷电价差自由掌控自身利润空间。

经过上述模型得到火电机组出力计划后，结合机组出力上、下限即可得到在不加入爬坡市场时，各个机组所具有的上、下爬坡能力，称其为机组自然爬坡能力，计算公式如下：

式中：$P_{i,t}^{{\text{up,c}}}$、$P_{i,t}^{{\text{dn,c}}}$分别为机组$i$在$t$时刻具有的自然上爬坡、下爬坡能力。

在得到火电机组自然爬坡能力后结合系统爬坡需求式(1)即可得到系统爬坡缺额，计算公式如下：

式中：$\Delta R_t^{{\text{up}}}$、$\Delta R_t^{{\text{dn}}}$分别为$t$时段系统上爬坡缺额和下爬坡缺额。

4.   计入火电、储能、需求响应与弃风弃光的主能量与爬坡联合出清模型

4.1   火电机组虚拟报量与虚拟报价

火电机组在参与电能量市场以及其他辅助服务市场时需要进行电量和价格的申报，调度机构根据申报信息完成优化出清。目前国内外研究普遍认为，火电机组参与爬坡市场按照机会成本定价，即机组为预留部分容量参与爬坡市场而在电能量市场中损失的获利。因此，本文在爬坡市场中火电机组无需单独报价，只需申报爬坡服务速率即可，机组的爬坡价格及中标量通过爬坡与主能量市场联合出清获得。为了进行爬坡市场出清计算，本文通过构建“虚拟报量”及“虚拟报价”实现电能量与爬坡辅助服务市场的联合出清^[9]。各火电机组虚拟报价计算公式如下：

式中：$\Delta C_{i,t}^{\text{f}}$为火电机组的虚拟报价；${\lambda _t}$为t时段不区分节点的系统边际电价；$C_{i,t}^{\text{f}}$为火电机组的电能量市场报价。

当$\Delta R_t^{{\text{up}}}$与$\Delta R_t^{{\text{dn}}}$均小于零时，此时系统不存在爬坡缺额，无需开启爬坡市场，各机组按照常规调度计划发电即可；当$\Delta R_t^{{\text{up}}}$或$\Delta R_t^{{\text{dn}}}$大于零时，系统自然爬坡能力难以应对系统爬坡需求，此时引入爬坡市场，爬坡容量相关约束起作用，常规经济调度结果被改变，此前申报爬坡速率的火电机组需预留出部分容量参与爬坡辅助服务市场，各机组可以预留的容量即为爬坡虚拟报量。虽然此前文献[9]已提出虚拟报量的概念，但仅针对满发机组，对于未满发机组的上、下爬坡虚拟报量难以适用，对此本文改进的火电机组上、下爬坡虚拟报量计算公式如下：

式中：$P_{i,t}^{{\text{up}}}$为机组$i$在$t$时刻上爬坡虚拟报量；$P_{i,t}^{{\text{dn}}}$为机组$i$在$t$时刻下爬坡虚拟报量；$P_{i,t}^{{{\text{G}}_{{\text{en}}}}}$为机组当前出力。式(16)第一个分式表示上爬坡虚拟报量，其含义是为下一时段自身上爬坡做准备，该机组在当前时段能够减少的最大出力值。式(16)第二个分式表示下爬坡虚拟报量，其含义是为下一时段的其他机组下爬坡做准备，该机组在当前时段能够减少的最大出力值。

本文中上爬坡虚拟报量和下爬坡虚拟报量均为机组相较于常规调度结果可降低的出力值，只有虚拟报价大于等于零的机组才存在虚拟报量，电力市场中未中标的机组不参与爬坡辅助服务市场。其中，上爬坡虚拟报量表示机组在当前时段可以适当减少出力而为下一时段的上爬坡做准备，当前时段能够减少的最大出力即为申报的上爬坡虚拟报量。下爬坡虚拟报量略有不同，某些机组在当前时段降低出力而让其他出力较低的机组优先发电，此时，下一时段出力较低的机组下爬坡能力增强，从而实现系统整体下爬坡能力的提升。

图 3说明了系统引入爬坡辅助服务市场前后，系统爬坡能力的变化。假设两台机组参数完全相同，某一时段在电能量市场出清的中标量分别为P₁和P₂，图 3(a)为不考虑爬坡辅助服务市场的出清结果，系统上爬坡能力为两个红色部分之和，下爬坡能力为两个绿色部分之和。假设此时系统存在上爬坡缺额($\Delta R_t^{{\text{up}}} > 0$)，引入爬坡辅助服务市场后的出清情况如图 3(b)所示，机组1在当前时段降低了部分出力P_A1–P_B1，降低的部分出力由机组2提供，此时，在保持当前时段负荷平衡的前提下，下一时段系统的上爬坡能力得到了增强(图 3(b)红色部分相加)，同时下爬坡能力保持不变。机组1出力变化量P_A1–P_B1即为其上爬坡虚拟报量的中标量。

图  3  引入爬坡辅助服务市场前后系统爬坡能力示意图

Figure  3.  Sketch map of the system's ramping capacity before and after the introduction of the market for ramping assistance services

下载: 全尺寸图片 幻灯片

图 3(c)与图 3(d)为系统存在下爬坡缺额的情况($\Delta R_t^{{\text{dn}}} > 0$)，图 3(c)为不考虑爬坡辅助服务市场的出清结果，系统总体下爬坡能力为两个绿色部分之和。引入爬坡辅助服务市场后出清结果如图 3(d)所示，机组1在当前时段降低了部分出力P_C1–P_D1，降低的部分出力由机组2提供，仍能维持当前时段负荷平衡，此时，系统下一时段下爬坡能力增强(图B绿色部分相加)，同时上爬坡能力保持不变。机组1出力变化量、P_C1–P_D1即为其下爬坡虚拟报量的中标量。

4.2   避免双重收益机组补偿机制

本文通过虚拟报量、虚拟报价的方式进行爬坡与主能量市场联合出清，确定各机组因爬坡而丧失电能量市场收益，由此产生的机会成本量，即机组的出力降低值，并对此进行爬坡补偿。机组的自然爬坡能力不进行爬坡市场补偿，而在电能量市场中进行结算，避免了出力增多的机组同时获得电能量市场与爬坡市场收益的问题。

同时，由于系统可能在同一交易时段既存在上爬坡缺额又存在下爬坡缺额，在进行市场出清时同一机组可能存在上爬坡虚拟报量中标量与下爬坡虚拟报量中标量均大于零的情况，为避免对火电机组爬坡容量进行双重补偿，在实际补偿时，取二者最大值作为补偿容量进行补偿，这有利于市场价格信号的合理传导。

在爬坡市场中，上爬坡能力的提升是由当前时段降低出力的机组实现，故补偿对象为上爬坡虚拟报量的中标机组，补偿容量为该机组虚拟报量的中标量，补偿价格按照边际价格结算。在下爬坡中，下爬坡能力的提升是由当前时段增加出力的机组实现，但该机组在电能量市场中并没有损失利益，真正产生机会成本的机组为当前时段降低出力的机组，即下爬坡虚拟报量的中标机组，故对该机组进行补偿，补偿容量为该机组虚拟报量的中标量，补偿价格按照边际价格结算。

以图 3为例，在图 3(a)到图 3(b)过程中，机组1在当前时段降低了部分出力，在电能量市场中做出了“牺牲”，需对机组1进行补偿，该部分成本即为机组1的上爬坡成本，机组2则无需补偿，补偿容量即为机组1降低出力(P_A1–P_B1)。在图 3(c)到图 3(d)过程中，虽然是机组2提升了系统下爬坡能力，但机组1在当前时段降低了出力，在电能量市场中做出了“牺牲”，故补偿对象仍为机组1，补偿容量为机组1降低出力(P_C1–P_D1)，机组2无需补偿。

4.3   储能参与爬坡市场

储能资源能够有效实现电能转换、储存和利用，由于其具有响应速度快、可以双向调节的特点，有助于提升电力系统运行的灵活性并可以促进可再生能源消纳^[13]。本文加入电网侧储能参与电能量市场出清，一方面能够有效平抑峰谷差，提升系统运行稳定性；另一方面能够减少风光资源浪费，降低系统运行成本。引入爬坡辅助服务市场后，在新能源占比过高的情况下，可能存在仅凭火电机组难以满足系统爬坡需求的情况，此时储能机组在参与电能量市场的基础上，同时参与爬坡辅助服务市场，利用其灵活调节特性应对系统爬坡不足，减少弃风弃光与切负荷事件的发生，进一步降低系统运行成本，提升系统的灵活性与稳定性。

储能在参与完成电能量市场出清后，各时段的充、放电计划已经确定，结合储能充、放电效率与荷电状态可以得到储能机组在时间间隔为1h时的爬坡能力，计算公式如下：

式中：$P_t^{{\text{up,c,e}}}$、$P_t^{{\text{dn,c,e}}}$分别为储能在$t$时刻的上、下爬坡能力；${u_{{\text{ch}},t}}$和${u_{{\text{dis}},t}}$分别为储能在$t$时刻的充电状态和放电状态。

加入储能机组参与爬坡辅助服务市场后，上式(14)爬坡缺额计算公式修改如下：

本文虽未考虑储能的收益，但为了实现总运行成本最小，储能机组会被尽量安排在电价低谷时段充电、电价高峰时段放电，在加入爬坡辅助服务市场后，储能原本充、放电计划被改变，在电能量市场中产生机会成本，但储能涉及多时段充、放电计划，在某一时段减少的中标电量可能转移到其他电价相近的时段，因此储能机组的机会成本难以核算，在本文中储能机组参与爬坡辅助服务市场的补偿价格根据储能度电成本确定^[27]，此价格高于火电机组参与爬坡辅助服务市场的边际价格。

4.4   出清模型与求解方法

在系统自然爬坡能力确定后，当存在任一时段系统自然爬坡能力不能满足爬坡需求时，进行电能量-爬坡联合出清。此时引入火电机组出力增加量$\Delta P_{i,t}^{{\text{f,add}}}$、火电机组出力减少量$\Delta P_{i,t}^{{\text{f,fold}}}$，储能充、放电变化量$\Delta P_{{\text{ch}},t}^{\text{c}}$、$\Delta P_{{\text{dis}},t}^{\text{c}}$，将上述模型中的$P_{i,t}^{{{\text{G}}_{{\text{en}}}}}$替换成$P_{i,t}^{{{\text{G}}_{{\text{en}}}}} + \Delta P_{i,t}^{{\text{f,add}}} + \Delta P_{i,t}^{{\text{f,fold}}}$，$P_{{\text{ch}},t}^{{\text{en}}}$替换成$P_{{\text{ch}},t}^{{\text{en}}} + \Delta P_{{\text{ch}},t}^{\text{c}}$，$P_{{\text{dis}},t}^{{\text{en}}}$替换成$P_{{\text{dis}},t}^{{\text{en}}} + \Delta P_{{\text{dis}},t}^{\text{c}}$可建立爬坡-电能量联合出清模型。

目标函数为系统总运行成本最小：

式中：$\Delta C_{i,t}^{\text{f}}$为火电机组$i$在$t$时刻的机会成本；$P_{i,t}^{{\text{up,en}}}$和$P_{i,t}^{{\text{dn,en}}}$分别为火电机组$i$在$t$时刻上爬坡和下爬坡虚拟报量的中标量；${\alpha _1}$和${\alpha _2}$分别为弃风弃光和需求侧响应补偿因子；$P_t^{{{\text{W}}_{\text{F}}}}$和$P_t^{{{\text{L}}_{\text{F}}}}$分别为系统弃风弃光量和需求侧响应量。

约束条件除去上述(3)—(11)外，还需增加的约束包括：

式(20)为爬坡虚拟报量中标量约束。式(21)中${u_1}$和${u_2}$分别为两个0-1变量，当上爬坡缺额大于下爬坡缺额时将${u_1}$置为1，反之${u_2}$置为1。式(22)表示机组出力的变化量，$\Delta P_{i,t}^{\text{f}}$大于0表示该机组出力增加，$\Delta P_{i,t}^{\text{f}}$小于0表示该机组出力减少。爬坡虚拟报量的中标量仅表示该机组能够提供用于置换的功率，但并不能一定提高系统爬坡能力，因此式(23)确保火电和储能参与爬坡市场后，系统整体爬坡能力能满足爬坡需求。此时，上述模型的约束条件均经过线性化处理，可以通过Gurobi求解器求解。

电能量和爬坡市场出清的影子价格为其对应的拉格朗日乘子，拉格朗日函数表示如下：

式中：${\lambda _{{\text{ramp - up}}}}$为上爬坡出清价格；${\lambda _{{\text{ramp - dn}}}}$为下爬坡出清价格。爬坡市场机组补偿的本质是对产生机会成本的机组进行补偿，因此，爬坡市场在结算时，对仅存在上爬坡或下爬坡虚拟报量中标量的时段按对应的上爬坡价格或下爬坡价格结算，在上爬坡与下爬坡虚拟报量中标量均存在时，取上爬坡价格与下爬坡价格中较大值，作为爬坡市场的结算价格。

5.   算例分析

5.1   基本参数

本文以我国西北某省份2022年某日的电网实际运行数据为研究对象，具体机组出力与负荷曲线见图 4。该省装有75台火电机组208台风电机组，255台光伏机组，火电总装机容量为33558MW，总风电装机容量为15745MW，总光伏装机容量为15547MW，储能装机2000MW，其中新能源装机占比约为48%。

图  4  系统负荷及新能源出力预测曲线

Figure  4.  Load forecast curve and new energy output forecast curve

下载: 全尺寸图片 幻灯片

本文中市场主体采用单段报价，以1h为出清间隔进行市场出清，负荷需求与新能源出力曲线如附录A所示，风光出力预测最大误差为15%，弃风惩罚费用α₁=0.3元/(kW·h)，失负荷惩罚费用α₂=8元/(kW·h)，储能补偿为500元/(kW·h)。在MATLAB软件中通过YALMIP工具箱调用GUROBI求解器计算得到仿真结果。

5.2   系统自然爬坡能力算例结果

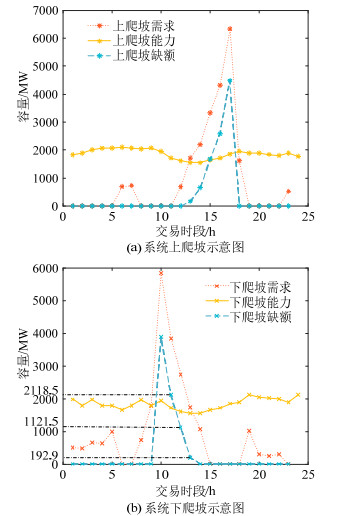
根据常规经济调度模型计算，确定系统自然爬坡能力，再与爬坡需求比较即可确定系统段上、下爬坡缺额情况，具体如图 5所示。系统上爬坡缺额主要集中在第13到第17交易时段，主要因为该时段内风光出力急剧降低，系统净负荷急剧升高，系统上爬坡需求持续增加，机组自然爬坡能力难以满足需求，导致出现上爬坡缺额。而系统下爬坡缺额集中在第9到第13交易时段，主要因为该时段内风光出力急剧增加，导致系统净负荷急剧降低，系统下爬坡需求持续增加，机组自然爬坡能力难以满足需求，导致出现下爬坡缺额。

图  5  火电参与爬坡市场前系统爬坡能力

Figure  5.  Sketch map of the system's ramping capacity before thermal generating units participate the market for ramping assistance services

下载: 全尺寸图片 幻灯片

图 5在第13交易时段既存在上爬坡需求又存在下爬坡需求，这主要是因为第13和第14交易时段风光出力相对稳定，波动较小，净负荷稳定，故系统确定性爬坡需求很低，但因为该时段风光出力极大，考虑风光出力最大预测误差，导致系统不确定性爬坡需求远大于确定性爬坡需求，故该时段既存在上爬坡缺额又存在下爬坡缺额。

最后通过图 4也可以看到该省份净负荷呈现出“鸭子曲线”形状，未来该省份随着新能源装机占比越来越高，“鸭子曲线”形态将越来越严重，届时系统爬坡缺额势必会越来越高，如不开展爬坡市场，系统的稳定性和安全性将面临重大冲击。

5.3   主能量-爬坡联合出清算例结果

5.3.1   不考虑储能参与爬坡市场

5.2节结果表明共计10个时段存在爬坡缺额，此时，仅考虑火电机组以虚拟报量-虚拟报价的方式参与爬坡辅助服务市场后，系统上、下爬坡能力变化如图 6所示。

图  6  火电参与爬坡市场后系统爬坡能力

Figure  6.  Sketch map of the system's ramping capacity after thermal generating units participate the market for ramping assistance services

下载: 全尺寸图片 幻灯片

在火电机组参与爬坡市场后，第9时段下爬坡缺额消失，同时第11、12、13时段的下爬坡缺额减小，说明此阶段对火电各时段中标出力进行调整后，系统总体下爬坡能力得到提升，系统弃风、弃光量降低。但系统上爬坡缺额并未明显降低或消失，这主要是因为在第13—17时段系统新能源出力由峰值急剧降低，此时火电机组需由出力较低的状态迅速增加出力以满足系统负荷平衡要求，由于在第13时段附近火电机组出力极低，基本不存在机组需要在当前时段降低出力而在下一时段增加出力的条件，因此各机组上爬坡虚拟报量基本为0，此时火电机组最大自然爬坡能力也已无法满足系统上爬坡要求，因此，此时系统需要通过其他方式增加上爬坡能力，降低运行风险。

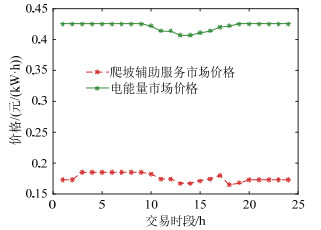
火电机组参与爬坡辅助服务市场后爬坡价格如下图 7所示。由于火电机组参与爬坡辅助服务市场的虚拟报价是按其机会成本计算，因此火电机组在爬坡辅助服务市场中的出清价格普遍远低于电能量市场出清价格。此外，由于系统仅需对火电机组虚拟报量中标量进行补偿，爬坡市场补偿成本一般较低，容易被系统所接受。

图  7  电能量市场与爬坡市场价格

Figure  7.  Electric energy markets prices and ramping market prices

下载: 全尺寸图片 幻灯片

5.3.2   储能参与爬坡辅助服务市场

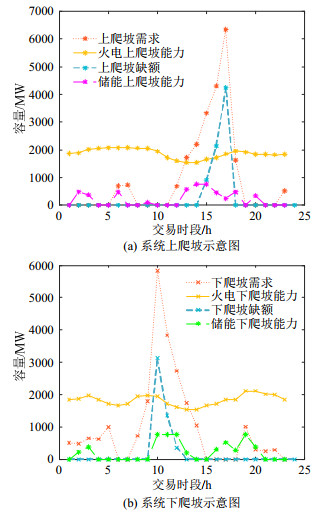
系统火电机组在以虚拟报量-虚拟报价的方式参与爬坡辅助服务市场后，系统下爬坡能力有所提高，但上爬坡能力几乎没有变化。此时系统电网侧储能以最大自然爬坡能力参与爬坡市场，一方面利用储能本身优良的调节性能，去增强系统爬坡能力，另一方面储能加入后可以增强火电机组调整出力的空间，有助于提高火电机组爬坡能力，加入储能后，系统爬坡能力如图 8所示。

图  8  储能参与爬坡辅助服务市场后系统爬坡能力

Figure  8.  Schematic diagram of system ramping capacity after energy storage participation in the ramping market

下载: 全尺寸图片 幻灯片

在火电与储能同时参与爬坡市场后，系统第13时段上爬坡缺额消失，第14—17时段的上爬坡缺额均有所减小。同时，系统在第13时段的下爬坡缺额消失，在第10—12时段的下爬坡缺额降低。可见在储能参与爬坡市场后，系统各时段爬坡能力得到显著增强，储能具体爬坡能力与其充放电状态及自身参数有关。

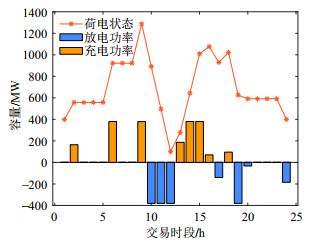
图 9为储能各时段充放电计划，在系统存在上爬坡缺额时段，储能会在保证火电机组上爬坡能力基本不变的前提下进行充电，如果在实际运行中系统发生上爬坡不足的情况，储能会将充电状态转变为以最大放电功率放电的放电状态，从而最大化储能的上爬坡能力。同样的，在系统存在下爬坡缺额的时段，储能会在保证火电机组下爬坡能力基本不变的前提下进行放电，当系统发生下爬坡能力出现不足的情况时，储能自身有足够的容量以最大充电功率进行充电，从而能够最大化自身下爬坡能力。

图  9  储能参与爬坡辅助服务市场后充放电计划

Figure  9.  Energy storage participation in the ramping market after charging and discharging programs

下载: 全尺寸图片 幻灯片

通过上述算例可以看到，储能参与爬坡辅助服务市场后，系统整体爬坡能力得到极大加强，系统弃风弃光量需求响应量均降低，主要得益于储能在进行充电与放电状态转换时能实现双倍调节。

如表 1所示，在开展爬坡市场后，系统在电能量的购电成本会有小幅增加，但弃风弃光和需求侧响应等事故成本大幅降低，系统运行的经济性增强。同时，在储能参与爬坡市场后，系统新能源消纳率得到大幅增加。

表  1  系统运行成本对比

Table  1.  System operating cost comparison

出清阶段	能量市场成本/元	弃风弃光成本/元	需求响应成本/元	爬坡成本/元	新能源消纳率/%	总购电成本/元
常规经济调度出清	244509412.2	2498083.0	76497920.0	0	91.43	323505415.2
储能不提供爬坡	244518990.1	2198178.0	76497920.0	84304.7	91.81	323299392.8
储能提供爬坡	245269309.1	1456299.0	58360558.5	5453970.3	94.57	310540136.8

下载: 导出CSV 

| 显示表格

目前山东爬坡市场采用爬坡与主能量联合一次性出清，而本文设置常规电能量市场出清和爬坡与电能量市场联合出清两轮出清，虽然增加了市场出清流程，但实现了对产生机会成本机组的精准补偿，有效降低了爬坡市场补偿成本，提高了系统运行的经济性。表 2是本文所提方法与山东出清方式的经济性对比。

表  2  平均成本对比

Table  2.  Comparison of average costs

方法	能量市场购电成本/元	爬坡市场成本/元
本文方法	310789363.41	84304.7
山东	305560407.2	8524635.55

下载: 导出CSV 

| 显示表格

其中电能量市场与爬坡市场各时段成本均采用边际价格×各机组发电量之和求取，由表 2可知，本文所提方法与山东现行方法相比，在爬坡市场的补偿费用大幅减少，这是因为本文不对机组自然爬坡能力进行补偿，仅对虚拟报量的中标量(机组出力减少量)进行补偿。自然爬坡能力部分机组出力根据电能量市场边际价格进行结算导致在电能量市场的购电费用有所增加。

综上可知，即使火电机组与储能均参与了爬坡市场，在总成本最低的目标下调整火电机组各时段的出力计划和储能各时段的充放电计划，系统上、下爬坡能力增强，但某些时段仍可能存在系统爬坡能力不足而需要辅以弃风弃光或切负荷手段维持系统稳定，这主要是因为新能源出力占比过高而且新能源出力峰谷差巨大，而火电机组在日前SCUC中已经固定开停机状态，在新能源出力峰谷转换时段，火电开机机组即使发挥全部爬坡能力仍难以满足系统爬坡需求，对此本文提出以下建议：

1）在日前和日内市场均开展爬坡市场，在日前进行SCUC模型计算时，由于加入爬坡需求约束，同一时段火电开机机组数有所增加，系统最大爬坡能力增强，但也会有不利影响，比如，此时可能有更多火电机组处于低出力水平，电能量市场价格可能会有所升高，电能量市场成本增加。同时，火电机组参与爬坡辅助服务市场的机会成本可能升高，爬坡补偿费用增加。此时电力调度机构可能需要权衡各方利弊，做出经济最优的决策。

2）在进行爬坡补偿费用分摊时，通过合理的方式将一定比例的爬坡补偿费用分摊到新能源机组，促进新能源发电主体提高自身出力预测精度，从而减少系统不确定性爬坡需求，降低系统爬坡补偿成本。

6.   结论

本文提出了一种包含储能参与的电能量与爬坡辅助服务市场联合出清机制，考虑火电机组虚拟报量-虚拟报价和储能固定价格补偿，构建了两阶段出清模型，增强了系统运行的灵活性，降低了系统运行成本，最后通过算例分析，得到以下结论：

1）一方面火电机组以虚拟报量-虚拟报价的方式参与爬坡辅助服务市场，可以根据虚拟报量中标量确定在电能量市场中真正“牺牲”的机组，另一方面同一机组可能同时中标上爬坡与下爬坡，取二者最大值进行补偿，避免了同一机组同时获取上爬坡补偿与下爬坡补偿。此外，算例结果表明，爬坡市场价格普遍远低于电能量市场价格。

2）在储能以固定补偿价格参与爬坡辅助服务市场后，系统新能源消纳率增长了3.14%，系统总运行成本大幅降低了12965278.4元。储能对增强系统调节能力，降低系统运行成本影响显著，为以后储能同时参与多种市场提供一定参考。

3）引入爬坡辅助服务市场后，会尽可能让各机组出力处于[最小出力+爬坡速度×单时段时间步长，最大出力–爬坡速度×单时段时间步长]之间，从而最大化系统爬坡能力，但系统购电成本增加了759868.0元。

本文目前暂且仅考虑电网侧储能参与爬坡辅助服务市场，储能无法通过决策决定自身获利情况，后续独立储能同时参与电能量与爬坡辅助服务市场时，独立储能的决策行为是今后的研究重点。此外，爬坡辅助服务市场加入后，系统存在购电成本增加量以及爬坡补偿费用如何合理分摊的问题也急需解决。