0.   引言

2021年7月我国正式启动全国碳市场，年度碳排放量大于2.6万t二氧化碳当量的发电企业成为第一批参与全国碳市场的市场主体^[1]。与此同时，中国诸多试点地区的电力现货市场已进入正式运行，市场化交易电量规模稳步增长。

尽管碳市场与电力市场各自独立运营，但由于发电行业是首批也是目前唯一被纳入全国碳市场的行业，电力市场和碳市场被同时参与两市场的发电商紧密地联系在一起^[2]。在电力市场和碳市场不断推进的背景下，发电商需要考虑两市场综合决策以寻求自身总收益最大化。对同时参与两市场的发电商行为和电-碳市场均衡结果进行分析，可帮助政策制定机构了解电-碳市场联动机理，支撑相应市场机制的完善，对市场的设计及监管具有重要意义^[3]。

研究电-碳市场联动作用的常见方法可分为两大类：计量经济分析方法和技术经济优化方法。前者基于实际市场数据采用多元回归分析、时间序列分析等数据驱动的方法分析电价与碳排放权配额(以下简称碳配额)价格间的传导关系，以此研究电力市场和碳市场间的相互作用^[4-7]；后者则是基于碳市场和电力市场运行机制，对市场主体行为和市场出清进行建模，依托不同的参数假设和情景设计分析模型输出结果，以此研究两市场间的相互作用和市场主体同时参与两市场的行为^[8-10]。

由于技术经济优化方法不依赖于实际市场数据，且能更好观察市场主体行为和市场均衡过程，更适合用于前瞻性研究，故本文主要采用此研究思想。使用该方法进行电力市场与碳市场联动分析的基本思路是对排放二氧化碳的化石能源发电商建模，由于其既参与电力市场又参与碳市场，故可将其作为联结两市场的纽带，建立发电商综合收益模型^[11-12]。同时考虑碳市场和电力市场的限制，通过优化发电商的竞价策略求解电-碳市场均衡结果^[13]。

现有电-碳市场联动研究存在两个尚未解决的关键问题：

一是没有实现电力市场与碳市场间的联动建模。大部分文献假定碳配额价格为固定值且对发电商设置固定的碳排放量约束^[14]，未采用模型内生的碳配额价格，此场景只适用于研究碳市场对电力市场单方面的影响，无法研究电力市场变化对碳市场的影响，无法模拟电力市场和碳市场相互影响共同达到均衡状态的实际情况。

二是现有模型未能处理好电力市场和碳市场的多时间尺度耦合关系。现有文献往往只分析现货阶段或只分析中长期阶段的电力市场与碳市场作用效果，两种建模都未能完全考虑电-碳市场在多种时间尺度下的耦合。仅研究现货阶段某时刻电-碳市场耦合的文献需要将发电商的全年碳市场行为拆分^[15]，大多文献将全年碳配额平均拆分，对发电商的碳排放量设置固定数值约束，没有考虑碳市场策略的全年综合优化，只对碳市场参数进行了简单的全年平均拆分，忽略了电-碳市场在长时间尺度上的耦合^[16]，不符合市场实际情况的建模，导致研究结果缺乏说服力。仅研究中长期阶段电-碳耦合的文献没有考虑现货阶段碳配额价格和电价的联动形成过程，将碳配额价格当作已知的全年固定值^[14]，但碳配额价格选取将对模型可信性产生重要影响，且忽略了对电力现货市场的考虑，不能用于研究两市场间的价格联动关系，无法模拟电-碳市场的短期均衡，未能做好电-碳市场在短时间尺度上的耦合。

综上，针对现有研究在电碳市场联动均衡和多时间尺度耦合两方面存在的问题，本文创新性地建立了发电商电-碳市场两阶段决策模型，通过模拟发电商在中长期和现货阶段电-碳市场的行为，实现了对电力市场和碳市场耦合在现货和中长期两种时间尺度下的建模，又通过设置两阶段决策间的约束和策略的滚动修正将发电商不同时间尺度的决策相连接，最终实现了电-碳市场多时间尺度耦合。同时，本文模型还解决了以往研究中假定碳配额价格和碳排放量固定的问题，实现了对碳配额价格内生的建模。最后，使用IEEE 30节点系统进行仿真计算，验证了模型的有效性。以期为后续中国电-碳市场协同发展路径规划与政策设计提供建议。

1.   电-碳市场耦合关系分析

1.1   碳市场交易基本原理

碳市场是以控制碳排放为目标、以碳排放权为主要交易产品的市场。碳市场针对碳排放量设定上限并设立交易市场，通常分为一级碳市场和二级碳市场。一级碳市场为政府无偿分配或拍卖交易，以实现长时间尺度下碳配额的初始分配。二级碳市场为短时间尺度的碳配额现货交易市场，市场主体根据排放情况自由进行碳配额交易以保证履约顺利完成^[17]。二级碳市场由独立的环境交易所组织交易，交易结果在当天完成结算。

1.1.1   一级碳市场

发电商在一级碳市场获得初始碳配额，初始碳配额的准确值根据该发电商在履约期的实际发电量核算。我国碳市场的初始碳配额分配方法具有以下3个特点：一是全部免费分配，现阶段所有初始配额实行全部免费分配。二是基于行业基准值，分配的初始碳配额量采用行业基准法进行核算，对不同发电技术、不同类别的机组设置单位电量碳排放限值。三是基于强度分配，发电商的初始碳配额分配量等于其对应的碳排放强度基准值与实际发电量的乘积。基于强度分配碳配额是中国碳市场较其他国家碳市场的显著不同，以欧盟碳市场为例，每个企业的初始配额是按照总量进行分配的，与实际发电量无关，而在基于强度的碳市场中企业获得的配额总量是由实际发电量计算得出的。

1.1.2   二级碳市场

受发电商自身碳排放强度影响，不同发电商实际排放量可能高于或低于其分配到的初始碳配额。为此，发电商需要根据碳配额价格、发电情况、碳配额使用情况等因素在二级碳市场进行交易。

如果发电商碳排放强度大于对应基准值，则需要在二级碳市场中购买不足的碳配额，如果发电商碳排放强度小于对应基准值，则可以在二级碳市场中出售盈余的碳配额。需要强调的是，即使发电商在某时段的碳配额拥有量小于其实际碳排放量，其发电也不会受到限制，发电商可以在当前履约期结束前任意时段在二级碳市场中购买碳配额以补足缺口。为实现自身利益最大化，超排的发电商会尽可能选择在碳配额价格较低的时段购买碳配额，有碳配额盈余的发电商会尽可能选择在碳配额价格较高的时段卖出碳配额^[18]。

在履约期结束时，监管机构会对碳市场参与主体的碳排放情况进行核查，并根据核查结果对碳配额进行清缴，发电商需要缴纳履约期内碳排放总量对应的碳配额。

1.2   电力市场与碳市场间的耦合关系

电力市场与碳市场由于具有相同的参与主体而存在复杂的耦合关系。本节将从市场交易数量、市场交易价格、市场运行时间三重角度介绍电力市场与碳市场的耦合关系。

1.2.1   电-碳市场数量耦合关系

电-碳市场间的数量关系主要体现在实际发电量与碳配额量的相互影响上。发电商在碳市场中的初始配额分配量和实际碳排放量是通过实际发电量计算得到的，数量关系满足下式：

式中：$\eta _{}^{{\text{allocate}}}$为发电商$0 \sim T$时段内的碳配额初始分配总量；$q_t^{\text{G}}$为发电商$t$时段的中标电量(假设实际发电量与中标电量相同)；${\varphi _0}$、$\varphi$分别为发电商发电类型对应的碳排放强度基准值和发电商发电的实际碳排放强度；$e$为发电商$0 \sim T$时段内的实际碳排放量；$\zeta$为$0 \sim T$时段内发电商实际碳排放量与其得到的初始碳配额的差额，为正说明发电商有富余碳配额可在二级碳市场中卖出获得收益，为负说明需要买入碳配额以满足碳配额清缴。

式(1)—(3)表明碳配额量和实际发电量之间存在相互影响的关系：

一方面，实际发电量影响碳配额量。通过电力市场出清得到的发电商实际发电量，其不仅直接影响发电商在碳市场中的初始配额分配量，而且影响到该发电商的实际碳排放量。可以看出发电商配额的盈余与缺口由该发电商的实际碳排放强度与行业碳排放强度基准值情况决定，数量受到实际发电量的影响，发电量越多，盈余/缺口越多。

另一方面，碳配额量影响发电商的实际发电量。对发电商而言碳配额量即碳配额的盈余和缺口情况，会直接影响发电商的碳配额交易量，由于碳配额买入成本(或卖出收入)和碳配额交易量呈正相关关系，碳配额买入成本(或卖出收入)又影响着发电商的发电成本^[19]，所以碳配额量影响发电商在电力市场中的决策，进而影响其中标量和实际发电量。

上述分析表明，电力市场与碳市场间存在着数量上的约束关系，也存在数量上的相互影响。

1.2.2   电-碳市场价格传导关系

碳市场中，碳配额符合商品的特点，其价格主要由市场供求关系决定。在长时间尺度下，各个发电商参与电力市场的出清结果和其碳排放情况会直接影响到碳配额供求关系。而短期碳配额价格主要围绕长期供求关系进行小幅波动，波动主要是由二级碳市场中的供求关系或预期供求关系变化造成。若二级碳市场中更多的发电商倾向于卖出碳配额，此时市场表现为供大于求，供应方会降低自身在碳市场中的报价，进而引起碳价的降低；反之，当供不应求时，需求方会提高自身在碳市场中的报价从而引起碳价的提升^[20]。因为电力行业占有绝大部分碳市场份额，所以电力市场的出清顺序、发电量、电价等情况都将显著影响碳配额供求关系，进而影响碳配额的长期价格和短期价格。

同时，碳配额价格也会影响到电价。由于发电商购入碳配额的花费(或卖出碳配额的收益)会直接影响发电成本，因此碳配额价格将会影响到发电商决策，并进一步影响电力市场出清结果^[21]。

1.2.3   电-碳市场时间尺度耦合

现有文献大多仅对两个市场的某一时刻建模，使电力市场和碳市场在某时刻同时出清，这既不符合碳市场按年履约的特点，也不符合两市场时间尺度不同的现状。

电力市场和碳市场的交易周期和交易频率均不同，两者交易的时间尺度如图 1所示。碳市场的履约期以年为单位(通常为一年)，在开市日的规定时段内可随时进行二级碳市场交易，发电商只要保证在履约期结束时碳配额清缴数量满足要求即可。而电力市场的中长期交易是以年、月、周为单位，现货交易以天、小时单位。因此，在碳市场的一个履约期内电力市场和二级碳市场都可以多次出清与结算。

图  1  电力市场与碳市场的时间尺度关系

Figure  1.  Time scale relationship between power market and carbon market

下载: 全尺寸图片 幻灯片

由分析可知，大多数文献将固定碳配额值作为某时段出清约束的做法是不符合实际的，电力市场和碳市场间的耦合约束应当被放在整个履约期内考虑，即使采用分配策略对全年碳配额进行预分配，预分配的碳配额也不应当被视为某段时间内的强制出清约束。

本文将电-碳市场耦合按照耦合时间长度不同分为长时间尺度耦合和短时间尺度耦合。长时间尺度以碳市场履约期为边界，电力市场和碳市场满足从当前时间点至履约期结束时的数量、价格关系。短时间尺度以一次电力现货交易时间为边界，电力现货市场和二级碳市场在一次电力现货交易周期中达到均衡，同时出清，得到该时段的电力现货价格和二级碳市场价格。

由于发电商的中长期决策和现货决策间存在相互影响的关系，同时短期市场和长期市场间存在价格上的传导关系和数量上的约束关系，因此电-碳市场的长时间尺度耦合和短时间尺度耦合间也存在复杂的联动关系，不能在研究某种时间尺度的电-碳市场耦合时忽略另一种时间尺度的影响。

1.3   发电商两阶段决策与电-碳市场双层模型

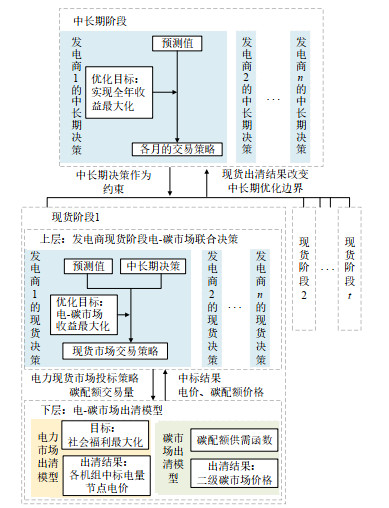
针对上述结合实际市场情况分析的电-碳市场多重尺度耦合机理，为研究电-碳市场的多时间尺度耦合，指导发电商综合考虑全年电、碳市场情况，本文提出一种电-碳市场多时间尺度耦合模型。以考虑多时间尺度耦合下的发电商同时参与电-碳市场的两阶段决策模型为纽带，使较短时间尺度的电力现货市场、二级碳市场和长时间尺度的碳市场年履约要求产生不同于强制碳排放约束的联结，研究电-碳市场在不同时间尺度内和不同时间尺度间的耦合，模型具体框架如图 2所示。

图  2  电-碳市场多时间尺度耦合模型框架

Figure  2.  Coupled multi-timescale modelling framework for power-carbon market

下载: 全尺寸图片 幻灯片

在中长期阶段，发电商同时参与电力市场和碳市场，其行为会影响到两市场的供需关系，继而影响到两市场的价格。本文通过发电商在电-碳市场中的中长期决策连接两市场，模拟长时间尺度下的电-碳耦合。

在现货阶段，电力现货市场和二级碳市场相互影响，达到均衡。本文构建了上层为发电商现货阶段电-碳市场决策，下层为电力市场和碳市场同时出清的双层模型，模拟了电力现货市场和二级碳市场的均衡过程，电力现货价格和碳配额价格由模型内生决定，反映了短时间尺度下的电-碳耦合。

在不同时间尺度衔接方面，由于发电商中长期和现货决策的相互影响，不同时间尺度下的电-碳市场自然地相互衔接。本文提出的发电商两阶段决策模型采用迭代求解、滚动修正的方法，不断根据最新现货市场出清情况和预测情况更新决策，实现了发电商的动态决策与多时间尺度下电力市场和碳市场的动态均衡。

2.   电-碳市场多时间尺度耦合模型

2.1   中长期阶段

2.1.1   发电商中长期交易策略分析

发电商在中长期决策阶段的目标是在全年时段下中长期电力市场收益加碳市场收益最大化(若卖出碳配额则碳市场收益为正值；若买入碳配额则为负值)。

本文假设发电商已签订好电力中长期合同，每月的中长期交易电量已经确定，发电商决策变量之一是每月碳配额交易量。对于碳排放强度大于行业基准值的发电商，其制定全年碳配额交易策略的目的是使其购买碳配额的成本最小，但是只有在履约期末发电商才能根据其实际发电量核定出该履约期的准确碳配额分配值，进而计算出准确的碳配额缺口数量。因此发电商在制定全年碳配额交易策略时需要考虑两个关键问题：一是如何准确确定全年碳配额分配量以计算碳配额缺口；二是在确定全年碳配额预计缺口的基础上，如何确定碳交易策略以实现低风险低成本买入所需配额缺口。对于碳排放强度小于行业基准值的发电商，策略制定同理，只是将对碳配额缺口的处理换成对碳配额富余的处理。

针对第一个关键问题，由于预测全年碳配额缺口的本质是预测发电商的全年发电量，而本文模型中假设中长期交易合约已经确定，因此如果能够准确预测发电商在现货市场的成交电量，就可以计算出较为准确的碳配额缺口。模型采用预测加修正的模式，在年初和每个月月末结合历史数据和当月实际发电量对未来的发电量进行预测，并更新全年碳配额分配量预测值，调整碳配额缺口预测值，具体流程见2.3节。需要说明的是，由于发电量和价格预测目前已有较多相对成熟的方法^[22-23]，故本文不再讨论预测算法，而是假设所有预测值均是基于已有预测算法的合理数据，预测误差不会影响本文模型的正常使用。

针对第二个关键问题，因为发电商在单个时段或单日的碳排放并无约束，仅需要在履约期结束时满足碳配额清缴要求即可。因此，发电商制定全年碳配额交易策略的基本原则是尽可能在碳配额价格低时买入碳配额以填补配额缺口。又由于碳配额价格预测值、发电商发电量预测值与真实情况往往存在一定偏差，仅根据预测值进行决策可能影响决策效果。

考虑到上述发电商制定碳配额交易策略的特点和目标，本文提出一种考虑碳配额价格波动和价格预测误差的中长期碳配额交易策略生成方式。

2.1.2   考虑价格波动和预测误差的中长期碳配额交易策略

对价格波动的考虑体现在每月碳配额交易量是受到该月碳配额价格预测值影响的，而非固定值；对预测误差的考虑体现在每月碳配额交易量不是仅由预测值决定的，而是围绕每月预计碳配额缺口值考虑预测值情况进行修正得到的。具体思路和约束如下：

1）中长期碳配额交易策略步骤。

首先基于发电商的每月预计发电量，用发电量乘以发电类型对应的碳排放强度基准值计算得到发电商每月预计在一级碳市场中被分配到的初始碳配额值，并计算每月预计碳配额缺口值。

在确定每月预计碳配额缺口值的基础上，考虑到“低买高卖”的策略，按照碳配额价格预测值大小进行调整。若该月碳配额价格预测值大于全年平均碳配额价格预测值，则在该月少购入碳配额，反之则多购入，少购入的量和多购入的量由该月碳配额价格预测值大于或小于全年平均碳配额价格预测值的比例确定。

这种根据不同碳配额价格调整碳配额交易量的思路区别于以往文献的强制碳配额量约束，没有严格要求发电商在每月按照发电量对应的碳配额缺口购入，实现了碳配额交易的年度优化。

2）碳配额月度买入、卖出约束。

出于风险考虑，发电商每月买入碳配额量不能超过政府所分配初始配额的一定比例。否则可能会出现发电商在某时刻买入全年碳配额缺口的情况，不利于风险分摊，故设置最大买入量约束。

买入约束：

式中：$\eta _{m, i}^{\rm{buy}}$为发电商$i$在$m$月的碳配额买入量；$\mu$为月度碳配额交易买入上限系数；$Q_i^{}$为根据发电商$i$发电量分配给该发电商的年碳配额总量。

同理，设置最大卖出量约束，卖出碳配额不能超出当前所持有的碳配额总量。

卖出约束：

式中：$\eta _{m, i}^{\rm{sell}}$为发电商$i$在$m$月的碳配额卖出量；$Q_i^{\rm{extra}}$为发电商$i$当年的碳配额富余总量。

3）碳配额持有量约束。

为防止发电商过度的投机行为，监管机构对发电商碳配额持有上限进行限制，发电商持有的碳配额数量不得超过规定的限额。

式中：$g$为碳配额交易机构规定的碳配额持有系数。

4）最小交易量约束。

碳配额交易机构通常会规定碳配额最小交易量，若$\eta _{m, i}^{\rm{buy}} \ne 0$，则有：

若$\eta _{m, i}^{\rm{sell}} \ne 0$

式中：$r$为碳配额最小交易量，通常为1t。

2.1.3   碳市场履约约束

在碳市场履约期结束进行碳配额清缴时，发电商所持有的碳配额应当大于其发电所产生的碳排放总量。

式中：${\varphi _i}$为发电商$i$的碳排放强度；${\varphi _{i0}}$为发电商$i$发电类型对应的碳排放强度基准值；$Q_i^{\rm{final}}$为发电商$i$全年实际得到的年度碳配额分配总量；$q_i^{\rm{year}}$为发电商$i$履约期总发电量；$Q_i^{\rm{final}}$与碳市场中碳配额交易的净值之和不小于其年度发电的实际碳排放总量。

2.2   现货阶段

在前文中长期模型的基础上构建考虑发电商两市场决策的现货阶段电-碳市场联合出清模型。上层为发电商现货阶段电-碳市场协同决策，下层为二级碳市场交易和电力现货市场交易模型，模拟了电力现货市场和二级碳市场的均衡过程。并通过滚动优化修正发电商中长期决策传导至现货出清模块的参数，实现电力市场和碳市场的多时间尺度耦合。

由于2.1节中长期策略是以“月”为单位确定碳配额交易策略，因此本文以30天为一个周期对现货阶段发电商碳配额交易策略进行优化。在以中长期月度碳配额交易策略为约束的基础上，发电商以月收益最大化为目标制定现货阶段决策。

除机组发电约束，碳市场规则性约束等约束外，中长期阶段决策传导至现货的参数有：月度碳配额缺口需求量/月度碳配额富余可卖出量、年度合约电量分解到各月的发电量等，在现货阶段这些参数可被视为约束或边界条件。

2.2.1   发电商现货阶段电-碳市场协同策略

发电商在现货阶段的决策需要考虑电力市场和碳市场的综合收益，目标函数为两市场净收益最大化^[24]，以30天为一个周期进行优化。

式中：${o_{t, ij}}$为电力市场申报价格；$\eta _{t, i}^{\rm{buy}}$、$\eta _{t, i}^{\rm{sell}}$分别为发电商$i$在$t$时段申报的碳配额买入量、卖出量；在$t$时段(在本文算例中$t$时段的长度为1天，也可以为更短的时间，原理相同)，${o_{t, ij}}$、$\eta _{t, i}^{\rm{buy}}$、$\eta _{t, i}^{\rm{sell}}$为发电商的决策变量，发电商通过改变自身在电力市场中的报价和在碳市场中的报量使自身达到收益最大化；节点电价$p_{t, n}^{}$、发电量$q_{t, ij}^{}$、碳价格${\lambda _t}$由下层市场出清结果得到。

在$t$($t < 30$)时段，$p_{t + 1, n}^{}...p_{30, n}^{}$、$q_{t + 1, ij}^{}...\, q_{30, ij}^{}$、${\lambda _{t + 1}}...\, {\lambda _{30}}$采用预测值，$p_{t, n}^{}$、$q_{t, ij}^{}$、${\lambda _t}$由下层模型出清得到，同时模型生成$t\sim 30$时段的发电商决策，但只有当前时段($t$时段)的决策${o_{t, ij}}$、$\eta _{t, i}^{\rm{buy}}$、$\eta _{t, i}^{\rm{sell}}$被采用。在$t + 1\sim 30$时段重复上述过程，每次都使用最新负荷侧情况和未来预测值重新进行决策。当$t = 30$时，模型得到此时段的市场出清结果$p_{30, n}^{}$、$q_{30, ij}^{}$、${\lambda _{30}}$和发电商决策${o_{30, ij}}$、$\eta _{30, i}^{\rm{buy}}$、$\eta _{30, i}^{\rm{sell}}$，完成该月现货阶段发电商碳配额交易策略的优化。

发电商现货阶段电-碳市场协同策略需要满足如下约束条件。

1）发电商报价约束。

本文假设发电商采用分段式报价，${o_{t, ij}}$为$t$时段发电商$i$的第$j$段报价；$q_{t, ij}^{}$为发电商$i$第$j$段的中标电量，每段报价和中标电量需满足其上下限约束，同时报价需按照从低到高的原则，即第$j + 1$段报价大于等于第$j$段报价。

式中：$o_{t, ij}^{\min }$、$o_{t, ij}^{\max }$分别为第$j$段报价下限和上限，报价下限由发电成本和碳排放成本共同决定：

式中：$C_{t, ij}^{}$为发电商$i$第$j$段发电成本；${\overline \lambda ^{\rm{pre}}}$为全年碳配额价格预测平均值，考虑碳配额购买成本的报价下限确定方法把由于发电而需要在碳市场购入碳配额的花费视为一种成本，并和发电成本一起考虑在报价中。使用平均碳配额价格则体现了碳市场长期决策的特点，某一时刻的碳成本并不取决于当前时刻的碳配额价格，因为碳配额不是每时刻清缴的，若当前时刻碳配额价格过高则在其他时刻买入碳配额以补充缺口即可，卖出富余量同理。

2）月度碳配额约束。

现货阶段策略需要在中长期碳配额交易策略的框架下进行，将发电商的中长期决策视为现货阶段决策的约束条件，以保证发电商在二级碳市场中的交易量满足其中长期决策。当月碳配额买入量之和不小于由中长期碳配额交易策略确定的该月碳配额买入量，保证发电商的碳配额购买量足够填补其碳配额缺口。

当月碳配额卖出量之和不大于由中长期碳配额交易策略确定的该月碳配额卖出量，保证发电商的碳配额卖出量小于其碳配额富余量。

2.2.2   二级碳市场交易模型

碳配额与一般商品相似，价格由碳市场的供给和需求共同决定，本文近似认为对电力行业而言碳配额价格随供给与需求差额线性变化^[25]，满足碳配额稀缺性的特点。将碳配额价格表示为

式中：${d_{{{\rm{CO}}_2}}}$为描述碳配额价格随供给、需求差额变化情况的参数，由碳市场情况、配额分配方式、各企业边际减排成本等因素决定。

碳配额交易量和碳配额价格需要满足如下约束。

1）碳配额价格不为零约束。

在供给远远大于需求时碳配额价格近似达到0，碳配额价格始终不为负值。

2）买入约束。

式中：$\mu '$为月度碳配额交易买入上限系数，每日买入量不超过每月买入量的一定比例。防止出现发电商每月仅进行一次碳配额交易的情况，通过多次交易能有效分摊价格风险。

3）卖出约束。

和买入约束设置思路类似，每日卖出量不超过每月卖出量的一定比例。

约束公式(式(19)—(24))中的${\lambda _{t, {{\rm{CO}}_2}}}$、$\mu _{t, {{\rm{CO}}_2}}^{\min }$、$\mu _{t, \text{buy}}^{\rm{min}}$、$\mu _{t, \text{buy}}^{\rm{min}}$、$\mu _{t, \text{buy}}^{\rm{max}}$、$\mu _{t, \text{sell}}^{\min }$、$\mu _{t, \text{sell}}^{\min }$为对应约束的拉格朗日乘子。

2.2.3   电力现货市场交易模型

电力现货市场交易模型的目标函数为社会福利最大化。

式中：${b_{t, dk}}$为$t$时段需求$d$的第$k$段报价；$q_{t, dk}^{}$为$t$时段需求$d$的第$k$段竞标电量；$q_{t, ij}^{}$为$t$时刻发电商$i$的第$j$段中标电量。

电力现货市场交易模型需要满足发用电平衡约束、线路传输功率约束、用户竞标量上下限约束、发电商中标量上下限等常规电力现货市场约束，具体约束公式见附录A。

2.2.4   现货阶段双层模型求解

使用KKT条件等价代替下层优化问题，将原双层规划模型转化为单层规划问题求解。此时的单层优化问题为混合整数非线性规划问题，使用附录B线性化思路将其转变为混合整数线性规划问题^[26]，并运用MATLAB中的CPLEX求解器求解该问题。

2.3   基于电-碳市场耦合的发电商两阶段决策滚动修正

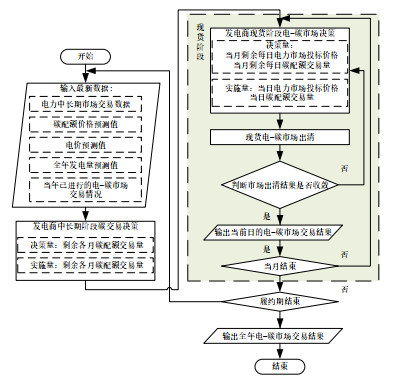
由于实际市场的情况和预测值之间存在偏差，因此发电商需要根据最新预测情况、已经发生的中长期和现货市场结果重新进行两阶段决策。全年的发电商两阶段决策滚动修正思路如下，示意图见附录C图C1。

1）在年初根据对电价和碳配额价格走势的预测情况按照2.1节中长期阶段的决策思路进行中长期电力市场决策和碳市场决策。

2）把步骤1）得到的中长期决策作为第一个月现货阶段电-碳市场的约束条件。在第一个月内按照2.2节现货阶段的决策思路进行30次发电商现货阶段决策和30次电-碳市场现货出清。

3）在第一个月结束时，结合第一个月电-碳市场的实际交易情况和最新的电价、碳配额价格预测数据，更新第二个月至履约期结束月的中长期策略。

4）以步骤3）得到的最新中长期决策为约束，进行第二个月的现货决策。

5）重复上述过程，直至当前履约期结束。

3.   算例分析

3.1   算例参数设置

本文选取IEEE 30节点系统^[27]模型对所提出的电-碳市场多时间尺度耦合模型进行仿真分析，共有6个发电商。为简化计算，设置两个策略性报价主体，一个为碳排放强度超过基准值的发电商A，另一个为碳排放强度低于基准值的发电商B，其余4个发电商按照发电成本加碳成本进行报价。具体参数设置情况见附录D。

3.2   发电商决策结果分析

本小节分析不同碳排放强度发电商的决策，定义实际碳排放强度高于对应碳排放强度基准值的发电商为“高碳排放强度发电商”，实际碳排放强度低于对应碳排放强度基准值的发电商为“低碳排放强度发电商”，则A、D、E、F为高碳排强度发电商，B、C为低碳排放强度发电商，以A和B为例分析不同碳排放强度发电商在电-碳市场中的决策。

3.2.1   高碳排放强度发电商决策结果

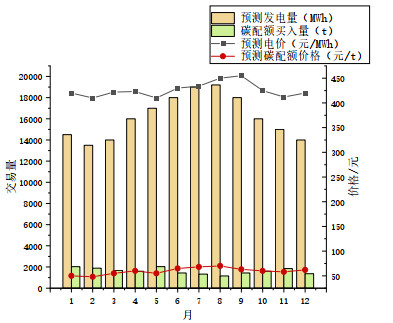
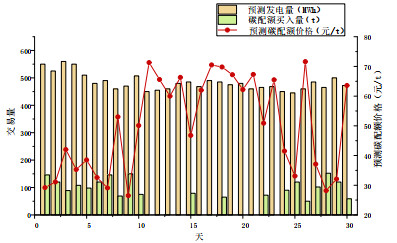
高碳排放强度发电商A的中长期阶段决策和现货阶段决策见附录E图E1、E2。

由发电商中长期碳配额交易策略可以看出在碳配额预测价格较高的月份，如8月，虽然预测用电量较大，但碳配额购买量并不多。这是因为在本文模型中发电商考虑了碳市场的履约和交易特性，进行了全年碳交易的优化，虽然发电量会直接影响碳配额缺口的大小，但依然会选择在碳配额价格较低的月份才购入大量碳配额以满足履约要求。

从发电商现货阶段电-碳市场交易策略可以看出，每日碳配额买入量主要受到碳配额预测价格的影响，而非预测发电量的影响。在碳配额预测价格较低的时段，如第28天，虽然发电量预测值并不高，但是碳配额买入量为152t，占全月碳配额买入量的7.5%。当碳配额预测价格过高时，如第11天，当天的碳配额买入量为零，发电商选择在其他时段买入所需的碳配额量。

3.2.2   低碳排放强度发电商决策结果

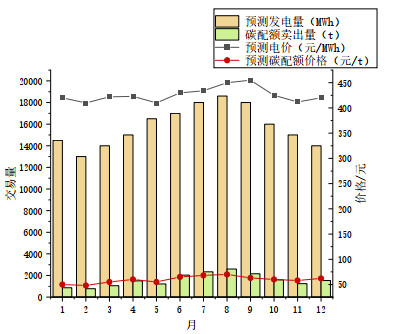
低碳排放强度发电商B的中长期阶段决策和现货阶段决策见附录E图E3、E4。

从低碳排放强度发电商的中长期决策和现货决策可以看出，低碳排放强度发电商倾向于在碳配额价格较高时卖出更多碳配额，如8月的中长期决策和第11天的现货决策，在考虑了电-碳市场联动的基础上实现了发电商全年决策优化，说明了本文模型的有效性。

3.3   与传统发电商决策模型对比分析

为说明本文提出的发电商两阶段决策模型的先进性，将本文模型与不考虑长期优化的传统决策模型结果进行对比分析：

传统决策1：发电商不进行碳交易策略的制定，在履约期即将结束时才购入自身碳配额不足量或卖出自身碳配额富余量。同时在决策阶段不考虑碳排放成本对自身发电成本的影响。

传统决策2：发电商将全年碳排放配额分配量平均分解至每天，若该天实际碳配额需求和分解至当天的碳配额量不相同，则在当天买入不足的碳配额或卖出富余的碳配额。此种决策与大多数文献将碳配额约束分解至电力市场每个时段的做法类似，没有考虑到决策的全年优化。

高碳排放机组A、D、E、F使用传统决策1、传统决策2与本文决策的全年碳配额购入成本情况如图 3所示。

图  3  不同决策下的发电商碳配额购买成本

Figure  3.  Costs of purchasing carbon allowances under different decision-making scenarios

下载: 全尺寸图片 幻灯片

可以看出，相比传统决策，使用本文提出的发电商两阶段决策模型可以实现“低买高卖”，高碳排放强度发电商在碳配额价格较低时买入了大量碳配额，在碳配额价格较高时买入配额量较少，降低了其全年碳配额购入成本。

研究电价、碳价均高于平均值的某用电高峰时期，高碳排放强度机组A采用本文决策思路和传统决策2思路进行决策的交易情况，结果如表 1所示。

表  1  不同决策下的发电商A现货阶段交易情况

Table  1.  Generator A spot-phase trading under different decisions

决策	中标电量/(MW·h)	电价/(元/(MW·h))	碳配额交易量/t	碳配额价格/(元/t)
本文决策	640	432	0	100
传统决策2	500	432	50	100

下载: 导出CSV 

| 显示表格

采用本文决策思路时，发电商在现货电能量市场中的最高报价为431元/(MW⋅h)，是边际发电成本与根据全年平均碳配额价格计算的碳成本之和，全部电量中标，碳配额买入量为0t。采用传统决策2时，发电商在现货市场中的最高报价为435元/(MW⋅h)，是边际发电成本与根据当前时刻碳配额价格计算的碳成本之和，中标电量500MW⋅h，碳配额买入量为50t。这一时段发电商A的竞价空间较少，报价时主要考虑边际成本，传统决策2的强制碳排放量约束使得发电商不得不在当前碳配额价格较高时刻买入所需碳配额，导致自身成本上涨，报价上涨，超过了市场出清电价，部分电量无法出清。使用本文决策时发电商则可以在其他碳配额较低时段买入碳配额，发电成本小于市场出清电价，全部电量出清，收益更高。

相较传统决策1，本文的两阶段决策模型更有计划性。传统决策1的碳成本主要与履约期末的碳配额价格相关。如果履约期末碳配额价格低，则碳排放强度较高的发电商可以以较少花费购入所需碳配额；但如果履约期末碳配额价格高，则发电商不得不花费很多资金在购入碳配额上，甚至可能计入碳成本后度电发电成本大于市场均衡电价，发电商亏损。本文模型能够保证发电商收益，减少碳配额价格不确定性带来的成本变化风险，使得发电商在全年都能有计划地进行碳市场和电力市场交易。

相较传统模型2，本文的两阶段模型灵活性更高，发电商收益更大。传统模型2虽然在全年各个时段都进行碳配额交易，但是每个时段的碳配额购入量(或卖出量)相同，本质上是把碳市场的履约责任拆分成了每天的强制碳排放约束，这种强制约束存在3点不足：首先是在某些时段会出现由于强制碳排放量约束限制发电的情况。在某些电价、碳配额价格都比较高的时段，电价高于发电商考虑平均碳配额价格计算的度电成本，这些时段发电商原本可以满发赚取利润，只要在其他碳配额价格较低时段购入碳配额以满足年度履约要求即可。但由于强制碳排放量约束的存在，发电商只能在当前时段以较高价格买入碳配额弥补缺口，导致当前时段考虑碳成本的度电成本上升。如本节算例所展示的情况，度电成本超过市场出清电价，发电商中标电量减少。其次是强制碳排放量约束忽略了碳市场决策的全年优化，碳配额购买成本大于本文提出的两阶段模型。如以发电商A的全年碳配额购买成本为例，使用传统决策2的碳配额购买成本为1155490元，使用本文模型的碳配额购买成本为1136336元，强制碳排放量约束导致发电商全年综合收益下降。最后，强制碳排放量约束忽略了预先分配的碳配额和根据发电量计算的实际碳配额分配值之间的偏差，强制碳排放量约束在履约期开始时根据预计的全年发电量确定。如果严格按照强制碳排放量约束进行全年发电活动，到履约期末若预计的全年发电量与实际的全年发电量不同，发电商的碳配额量可能有所富余或无法满足碳配额清缴，造成发电商利润损失。

本文提出的两阶段模型实际上是在传统模型2基础上的一种改进模型，放宽了每日的买入卖出约束，并且实现了全年交易的优化，使得碳配额交易灵活性更高，实现了对全年电-碳市场综合收益的优化。

综上，使用本文两阶段决策模型的全年收益显著大于传统决策模型1、2。本文模型考虑了全年决策优化，是有效的，能帮助发电商考虑多时间尺度耦合进行全年电-碳市场联合决策。

3.4   电-碳市场现货阶段均衡分析

使用本文考虑发电商两市场决策的现货阶段电-碳市场联合出清模型与未考虑电力市场和碳市场相互影响的模型进行对比，证明本文模型能够真实模拟电力市场与碳市场在现货阶段的相互影响。

场景1：使用本文所提出的现货阶段电-碳市场均衡模型进行分析。

场景2：仅考虑电力现货市场，不考虑二级碳市场，不设置碳排放量约束。

场景3：对每个时段设置固定的碳排放总量约束。

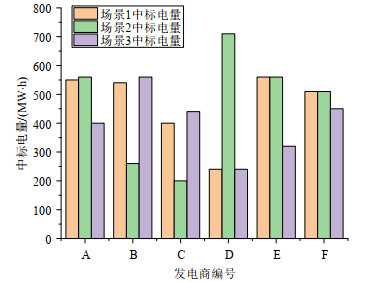
不同场景下各发电商的中标量如图 4所示，电价和碳排放量情况如表 2所示。

图  4  不同场景发电商中标电量变化

Figure  4.  Power bids from generators under different scenarios

下载: 全尺寸图片 幻灯片

表  2  不同场景下的电价和碳排放量情况

Table  2.  Electricity price and carbon emission under different scenarios

场景	碳排放总量/t	电价/(元/(MW·h))
场景1	1907.5	420
场景2	1980	416
场景3	1744.5	430

下载: 导出CSV 

| 显示表格

场景2中，各机组出清顺序主要受到发电成本的影响，发电成本低的机组优先出清，故发电成本较低的机组D、E、F的中标量较大。同时，由于此场景仅考虑电力市场，不考虑碳市场和碳排放量约束，所以电价是3个场景中最低的，碳排放总量是3个场景中最大的。

场景3约束了各机组的碳排放量，实际碳排放强度较高的机组由于碳排放量约束只能出清部分电量，故碳排放强度较高机组A、D、E的中标电量较场景2减少，碳排放强度较低机组B、C的中标电量较场景2增加。发电成本高碳排放强度低的机组优先出清导致此种场景下的电价最高，碳排放总量最低。强制碳排放量约束虽然可以快速实现全社会减碳的目标，但会导致电价过高，社会福利减少。

场景1(即本文考虑电-碳市场均衡的场景)中，各机组出清顺序同时受到发电成本和碳配额净购买成本的影响，综合成本较低的机组B、C、F优先出清，碳排放总量较只考虑电力市场的场景2更低，电价较设置强制碳排放约束的场景3更低，以较低的社会福利损失实现了碳减排。虽然此种场景没有设置强制的碳排放约束，但碳市场的存在使得发电商需要考虑碳成本进行报价，低碳排放机组的竞价优势更大，碳市场通过影响发电商行为最终实现碳减排目标。同时，场景1的电-碳市场同步均衡模型考虑到了电力市场与碳市场间的相互影响和电力现货价格与碳配额价格之间的相互传导关系，求得电价为420元/(MW⋅h)，碳配额价格为42元/t，实现了对两市场相互影响，同时达到均衡状态的模拟。

3.5   免费碳配额分配量对电-碳市场的影响

采用本文考虑发电商两市场决策的现货阶段电-碳市场联合出清模型，可以进一步探究碳市场参数设计对两市场均衡的影响。以不同碳配额量为例设置算例场景。

场景4：在场景1的基础上，将用于计算分配碳配额量的碳排放强度基准值提升15%，即增加免费碳配额的分配量，模拟放宽碳减排政策的场景。

场景5：在场景1的基础上，将用于计算分配碳配额量的碳排放强度基准值缩减15%，即缩减免费碳配额的分配量，模拟强化碳减排政策的场景。

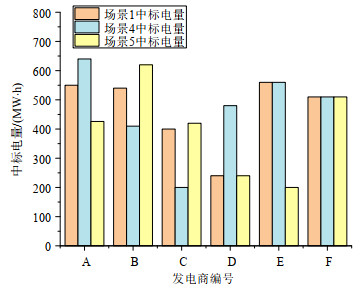
改变免费碳配额分配量后，电力市场的出清顺序发生变化，发电商中标量改变，各发电商的具体中标量如图 5所示，碳排放总量、电价、社会福利变化如表 3所示。

图  5  不同碳排放强度基准值下发电商中标电量变化

Figure  5.  Power bids from generators under different carbon emission intensity baseline

下载: 全尺寸图片 幻灯片

表  3  不同碳排放强度基准值下碳排放总量情况、电价、社会福利变化情况

Table  3.  All carbon emission, electricity price and social welfare under different carbon emission intensity baseline

场景	碳排放总量/t	电价/(元/(MW·h))	社会福利/元
场景1	1907.5	420	80091.25
场景4	1961	416.92	90037.6
场景5	1616.3	425.18	61347.7

下载: 导出CSV 

| 显示表格

当免费碳配额分配量增加时，碳排放强度较高的火电机组出清顺序提前，出清量增加。这是由于免费碳配额分配量增加时，碳配额价格降低，碳排放强度较高的火电机组度电碳成本降低，更具竞争优势。电力现货市场均衡价格降低，但社会碳排放总量增加。同时，分析发现策略性发电商A降低的报价小于由于碳配额分配量增加而减少的碳成本，发电商将碳成本完全转嫁至消费侧，发电商这一行为与欧盟碳市场初期相似。欧盟碳市场第一阶段给发电企业发放了过多的免费碳配额，导致碳配额价格较低，且很多发电商都有富余碳配额量可用于在碳市场出售。部分发电商以碳市场为由抬高电价，但实际的碳配额购买成本远小于其报价增加值，甚至还能够卖出多余的碳配额赚取收益，导致发电侧获得了大量超额收益。

当免费碳配额分配量缩减时，碳排放强度较高的机组出清顺序延后，其发电空间被碳排放强度较低的机组替代，部分碳排放强度较高的火电机组无法出清。这是由于免费碳配额分配量缩减，二级碳市场中的碳配额供不应求，碳配额价格明显提升，碳排放强度较高的火电机组度电碳成本显著提升，其报价随之提升；同时碳排放强度较低的机组由于碳配额价格提升，其在碳市场中收益增加，综合发电成本减少，报价随之降低。在需求侧情况不变的场景下，由于报价变化，不同发电商的出清顺序和中标电量发生变化，存在碳排放强度较高的火电机组报价高于市场出清价格而无法出清的情况。当免费碳配额分配量缩减过多时，甚至可能出现碳配额价飞升、电价过高、需求侧无法得到满足的情况。

过多的免费碳配额导致发电侧赚取大量超额利润且碳减排效果大打折扣；过少的免费碳配额使得碳配额价格和电价过高，虽然起到了减少碳排放的效果，但严重影响了社会经济活动的正常运行。因此，确定合适的免费碳配额分配值在碳市场政策制定中十分重要。

4.   结论

本文在深入研究电力市场与碳市场在数量、价格、时间耦合关系的基础上，针对现有研究对电-碳市场多种时间尺度耦合考虑不足的问题，建立了以发电商全年决策为纽带的、实现中长期阶段与现货阶段相互联动的电-碳市场多时间尺度耦合模型。并结合IEEE 30节点系统进行了算例分析。得出了如下结论：

1）对于发电商，本文提出的两阶段决策模型显著优于传统模型，它放宽了发电商每日的碳配额交易约束，从而提高了碳配额交易的灵活性，实现了发电商全年交易的优化，并有效提升了全年电-碳市场的综合收益，为发电商进行电-碳市场综合决策提供了科学依据。

2）本文以同时参与电力市场和碳市场的发电商为纽带，通过模拟发电商在中长期和现货阶段的行为，实现了对电-碳市场在现货和中长期两种时间尺度下耦合的建模，又通过对发电商两时段决策的连接最终实现了电-碳市场的多时间尺度耦合。同时，完成了对碳配额价格内生的建模，使模型能够实现对多时间尺度下电力市场与碳市场双向联动效果的分析。

3）本文模型在线性化后为混合整数线性规划问题，具有较高的求解效率，能够满足较长时间尺度仿真的需要。

4）碳市场的引入通过影响发电商发电所需支付或获得的碳成本影响发电商报价，继而影响发电商的出清情况，能够用市场化的方式引导碳排放强度较高的火电机组进行升级优化，主动降低碳排放强度。

5）过多的免费碳配额量可能会导致发电侧赚取大量超额利润、减排效果不显著；过少的免费碳配额量虽然可以大幅减少碳排放量，但会出现无法满足用电需求、影响社会福利的情况。因此，合理设定免费碳配额分配量成为碳市场政策制定的关键。

在后续研究中，可以重点关注电力市场与碳市场在多时间尺度上的深度耦合，研究可以通过构建更为复杂的多时间尺度决策模型，探索不同情景下的市场动态与均衡状态。当前所构建的模型虽然已在一定程度上满足了研究需求，并展现了良好的求解性能，但其潜在的局限性亦不容忽视。随着模型复杂度的增加和场景的多变，当前的求解方法可能会面临挑战，可考虑在后续研究中探索更多求解速度更快的算法，如元启发式算法及其混合策略、并行与分布式计算技术以及基于人工智能的算法优化等算法，并考虑对求解器进行更精细的配置和参数调整，以进一步提升求解效率。

附录见本刊网络版(http://www.dwjs.com.cn/CN/1000-3673/current.shtml)。

附录A

1）发用电平衡约束。

式中：${B_{t, nm}}$为$t$时段节点$n$到$m$的线路电纳；${\delta _{t, n}}$、${\delta _{t, m}}$分别为$t$时段节点$n$、$m$的相角；发用电平衡约束等式对应的拉格朗日乘子${\lambda _{t, n}}$为节点电价。

2）线路传输功率约束。

式中：$P_{t, nm}^{L\max }$为$t$时段节点$n$到$m$的线路最大传输功率。式(A3)表示将节点1设置为参考节点。

3）用户竞标量上下限。

4）发电商中标量上下限。

约束公式中的$\mu _{t, nm}^{L\max }$、$\mu _t^{\delta 1}$、$\mu _{t, dk}^{\min }$、$\mu _{t, dk}^{\max }$、$\mu _{t, ij}^{\min }$、$\mu _{t, ij}^{\max }$为对应约束的拉格朗日乘子。

附录B

目标函数中存在两变量相乘的非线性项$p_{t, n}^{}q_{t, ij}^{}$、${\lambda _t}\eta _{t, i}^{\rm{buy}}$、${\lambda _t}\eta _{t, i}^{\rm{sell}}$，约束条件中存在互补松弛条件对应的非线性项。

非线性项$p_{t, n}^{}q_{t, ij}^{}$使用对偶理论和互补松弛条件替换为下式：

非线性项${\lambda _t}\eta _{t, i}^{\rm{buy}}$、${\lambda _t}\eta _{t, i}^{\rm{sell}}$使用二进制展开法进行线性化，用满足以下约束的$\lambda _{t, q}^{\rm{ref}}\xi _{t, i, q}^{\rm{buy}}$代替${\lambda _t}\eta _{t, i}^{\rm{buy}}$。

式中，$\lambda _{t, q}^{\rm{ref}}$为将${\lambda _t}$按固定间隔分为$q$个离散数值所得取值；$\Delta \lambda _t^{\rm{ref}}$为两个离散数值的差值；$z_{t, q}^{}$为二进制变量，用于表示$\lambda _{t, q}^{\rm{ref}}$是否为与${\lambda _t}$最为接近的参考值；$M$为一个足够大的数；$\xi _{t, i, q}^{\rm{buy}}$为表征$\eta _{t, i}^{\rm{buy}}$的连续变量。当${\lambda _t}$落在某个范围内时，对应的二进制变量$z_{t, q}^{}$为1，其余各段皆为0，此时对应的$\xi _{t, i, q}^{\rm{buy}}$等于$\eta _{t, i}^{\rm{buy}}$，其余各段$\eta _{t, i}^{\rm{buy}}$为零。${\lambda _t}\eta _{t, i}^{\rm{sell}}$的线性化过程同理。

互补松弛条件对应的非线性项，可采用大M法进行线性化。

附录C

  C1  发电商决策滚动修正流程

  C1.  Rolling correction process for generator decisions

下载: 全尺寸图片 幻灯片

附录D

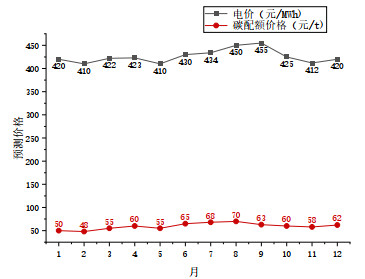
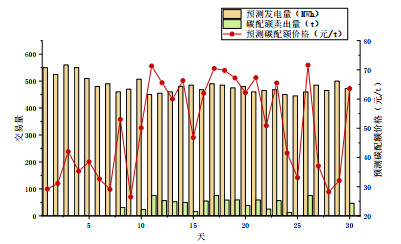
电力市场的中长期月度交易价格和碳配额月度平均价格预测值如图D1所示。

  D1  电价、碳配额价格预测情况

  D1.  Torecasts of electricity price and price of carbon emission quota

下载: 全尺寸图片 幻灯片

对于发电商的两阶段决策，本文算例以生成发电商第一个月的中长期决策和该月第一天现货决策为例进行展示，其余各天和各月的决策思路与之同理。若要采用本文模型进行全年模拟，需要结合发电商所使用的预测算法特点对预测误差变化进行建模，理想情况下可假设预测价格与实际价格的偏差服从正态分布，且标准差随预测时间与实际时间距离变长而变大。

采用分段修正方法结合每月预计碳配额缺口值和碳配额价格预测值情况得到每月碳配额交易量。以实际碳排放强度大于基准值的发电商为例，$m$月的碳配额买入量由以下公式确定：

其中${\lambda _m}$为预测的$m$月碳配额价格，$\zeta _{m, i}^{}$为发电商$i$在$m$月的预计碳配额缺口值。实际碳排放强度小于基准值的发电商确定每月碳配额卖出量的思路与之同理，只是将买入量改为卖出量。

本文将发电商的运行成本看作发电量的二次函数，关系式如下：

式中，${C_i}$为发电商$i$的发电成本；${q_i}$为发电商$i$的发电量；${a_i}$、${b_i}$、${c_i}$为二次函数各项系数。

发电商第一日现货阶段的参数见表D1，除发电成本系数外，其余参数和中长期阶段相同。

  D1  发电商参数

  D1.  Generator parameter sheet

发电商	实际碳排放强度/(t/(MW·h))	碳排放强度基准值(t/(MW·h))	发电成本二次函数系数			机组容量/MW	所在节点
			a	b	c
A	0.7	0.6	0.02397	410	0	640	1
B	0.5	0.6	0.01119	420	0	620	2
C	0.5	0.6	0.03995	424	0	620	5
D	0.75	0.6	0.05331	415	0	710	8
E	0.8	0.7	0.01598	412	0	560	11
F	0.75	0.7	0.01598	412	0	510	13

下载: 导出CSV 

| 显示表格

当发电侧只有一个策略性主体时，即单寡头情况时，为MPEC问题。当发电侧有两个或多个策略性主体时，为EPEC问题，本文使用对角化方法求解EPEC问题。

IEEE 30节点模型中有21个负荷，将21个负荷聚合为3个负荷聚合商L1、L2、L3，第一日现货阶段的负荷参数见表D2。

  D2  负荷参数表

  D2.  Load parameter

负荷聚合商	总需求/MW	三段式报价/(元/(MW·h))
L1	1200	(500, 425, 410)
L2	1200	(450, 427, 415)
L3	1200	(460, 430, 420)

下载: 导出CSV 

| 显示表格

附录E

  E1  高碳排放强度发电商中长期阶段决策

  E1.  Electricity forward market decisions of high carbon intensity power producers

下载: 全尺寸图片 幻灯片

  E2  高碳排放强度发电商现货阶段决策

  E2.  Spot market decisions of high carbon intensity power producers

下载: 全尺寸图片 幻灯片

  E3  低碳排放强度发电商中长期阶段决策

  E3.  Electricity forward market decisions of low carbon intensity power producers

下载: 全尺寸图片 幻灯片

  E4  低碳排放强度发电商现货阶段决策

  E4.  Spot market decisions of low carbon intensity power producers

下载: 全尺寸图片 幻灯片