Fast Short-circuit Protection Method for Low-voltage AC System With Distributed Photovoltaic
-
摘要: 低压交流系统过电流原理短路保护方法受限于短路检测特征单一，已难以满足复杂工况下系统运行保护，分布式光伏、储能等柔性装置接入给低压保护技术带来新挑战。因此，提出节点自治的含分布式光伏低压交流系统短路快速保护方法。首先，以短路电流、电压瞬时幅值构建支路状态特征，研究短路状态早期辨识方法。其次，引入同节点各支路短路电流极性信息，设计基于短路电流方向相关性辨识的短路支路保护决策机制。最后，进行低压真型系统及其仿真模型的保护实验。实验结果表明，传统支路和光伏并网支路的短路均可在0.5 ms内检出；不同节点间的保护响应范围合理搭配，且对于同一节点的近端短路，各支路可在短路1 ms内独立决断是否触发保护，保障了保护方法的选择性；保护方法在各类源荷运行工况扰动下不误动，研究成果具有较高的理论和工程价值。Abstract: Due to the limitation of a single short-circuit detection feature, the short-circuit protection method of a low-voltage AC system based on the over-current principle has been unable to meet the requirements of operation protection under complex working conditions. With the availability of flexible technologies such as distributed photovoltaic and energy storage, low-voltage protection technology has faced new hurdles. Therefore, a node-autonomous fast short circuit protection method for distributed photovoltaic low-voltage AC systems is proposed. Firstly, the characteristics of the branch state are constructed using the instantaneous amplitudes of short-circuit current and voltage, and the early detection technique of short-circuit state is investigated. Secondly, the polarity information of the short-circuit current in each branch of the same node is introduced, and the short circuit branch protection decision mechanism based on the direction correlation identification of the short-circuit current is designed. Finally, the protection experiment of the low voltage physical experiment system and its simulation model are carried out. The experimental results show that the short circuit of both the traditional and photovoltaic branches can be detected within 0.5 ms. The protection response ranges between different nodes are reasonably matched, and for the short circuit at the near end of the outlet of the same node, whether the protection is triggered can be accurately determine in each branch within 1 ms of the short circuit, thus achieving selective protection. The protection method does not malfunction under the disturbance of various source load operating conditions. The research results have high theoretical and engineering value.
-
0. 引言
随着分布式光伏、储能与柔性转供电等设备应用[1-3]，低压交流系统网络结构从单源辐射状向着多源网状演变[4]，现阶段采用上下级断路器过电流配合原理的传统保护方法，难以适用多端电源低压交流系统保护的选择性需求[5]。含功率变换器的分布式电源短路输出特性与网侧电源存在本质区别[6-7]，致使短路故障辨识难度加大，系统保护的快速性和选择性水平明显下降[8]。
为解决含分布式电源低压交流系统短路保护难题，众多学者进行了大量研究[9-11]。文献[12-13]在常规过电流保护基础上，引入附加信息对电流速断保护整定值进行自适应调整。该方法一定程度提高了过电流保护的灵敏度，但随着分布式电源容量与接入点增加，支路间保护难以配合，保护出口时延增加[14]。此外，分布式电源自身短路保护阈值低，保护灵敏度远高于常规断路器[15]，进一步加剧传统断路器与分布式电源间保护适配难度。因此，提高短路检测快速性与保护选择性是含源低压交流系统短路保护的研究重点[16]。
为优化含分布式电源交流系统保护的选择性问题，配电网率先引入基于光纤通信的电流差动保护方法[17-18]。文献[19-20]在计及光伏运行方式与控制策略对电流的影响，进一步提出基于5G通信的阻抗纵联差动保护方法。然而，相较于10kV配电网，低压交流系统层级、支路繁多，且分布式新能源数量大、分散性强。纵联差动保护因其配置难度和经济成本问题，难以在低压交流系统中推广应用[21]。文献[22]在短路故障早期检测的基础上，通过现场总线通信实现全系统范围内短路信息交换，并提出低压系统多层级全范围选择性协调保护系统技术概念，以提高短路保护的选择性与速动性。然而，该保护系统尚未考虑分布式电源接入的影响，且选择性保护决策需依赖主机完成，对于通信可靠性要求较高，应用场景有限。上述方法仅限于对传统保护方法的适应性进行改进，尚无法从根本上解决分布式电源接入的短路故障辨识准确性和多源拓扑短路保护响应选择性难题。鉴于低压系统层级支路多、线路短且源储装置分布式接入，短路电流、电压幅值变化大，甚至存在短路时支路故障电流方向反转的情况。因此，在传统低压交流系统保护选择性尚未解决的情况下，亟待研究含分布式电源低压交流系统的短路保护新方法。
本文根据含分布式光伏低压交流系统发生短路时的故障特性，提出基于短路状态早期检测与节点自治的短路快速保护方法。该方法首先通过改进最小二乘拟合快速计算短路电流电压时变幅值，并构造短路状态早期检测判据；然后，通过控制器局域网总线(controller area network，CAN)通信与高速电力线通信(high speed power line communication，HPLC)，进一步构建节点内区域自治、节点间协调配置的分布式短路保护决策机制；最后，经多层级低压交流真型实验系统的短路实验，验证了所提保护方法的有效性，并为含分布式光伏低压交流系统短路保护的工程应用提供了参考经验。
1. 含分布式光伏低压交流系统短路特性
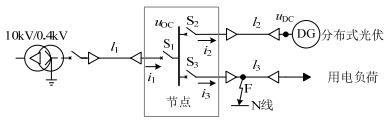
考虑分布式光伏在低压交流系统中已广泛普及，储能发电并网的短路输出特性与光伏相似，因此，本文以分布式光伏为代表，分析含源低压交流系统短路故障的电流、电压暂态特性。其中，含分布式光伏低压交流系统典型拓扑如图 1所示。图中：uOC为节点电压；uDC为光伏并网点电压；i1、i2、i3分别为支路l1、l2、l3的采样电流；S1、S2、S3为各支路断路器。
![]()
图 1 含分布式光伏低压交流系统拓扑图Figure 1. Topology of the low-voltage AC system with distributed photovoltaic以F点发生单相短路故障为例，可将短路电流来源分为主变供应、逆变器供应和混合供应3类。该简化模型覆盖含分布式光伏低压交流系统短路故障的不同支路场景，具有一定的普遍性。
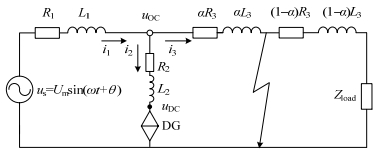
现有并网逆变器控制策略以电流环为内环、电压环为外环，并在此基础上设计诸如PQ控制法、下垂控制法等。但当逆变器交流侧发生短路时，交流侧电压跌落较大，电压环控制失效，仅电流环起作用。此时，并网逆变器输出电流受控于控制器和控制算法，短路时可将光伏系统等效为压控电流源[23]，得到短路故障简化模型，如图 2所示。
![]()
图 2 含分布式光伏低压交流系统单相短路简化模型Figure 2. Simplified model of single-phase short circuit in low-voltage AC system with distributed photovoltaic图中：uS为变压器侧等效电源，近似为无穷大电源；R1、L1、R2、L2、R3、L3分别为线路l1、l2、l3的等效电阻、电感；Zload为负荷等效阻抗；α用以表征短路点在线路l3中的位置，0≤α≤1；i2为逆变器输出电流。由于低压光伏逆变器大多采用PI环控制输出电流，且一般不具备无功补偿功能。因此，i2可由式(1)求得[23]：
{i2=P−1⋅[Id_setIq_set]Id_set=(Kp+KIsTd)⋅(Pref−U+DCId)Iq_set=Iq (1) 式中：P–1为Park逆变换矩阵；Id_set、Iq_set为电流交、直轴目标值；Kp、KI为电流PI环控制系数；Td为PI环的时间常数；Pref为直流侧供电功率，由于太阳能电池发电功率变化惯性较大，短时不变；U+DC为uDC的正序分量；Id、Iq为i2经Park变换后的交、直轴分量。
由于逆变器输出电流受控制器限制，最大输出不超过2倍额定电流[24]。短路时，i2与i1、i3数值相差较大，为使求解过程解耦，便于计算，可在求解i1时，忽略i2的影响。求得uOC后，再计算i2、i3。若需精确求解，可将i2回带，更新i1后进行迭代计算，直至误差收敛。通过上述方法，可得其余各支路电流与节点电压的近似表达式：
{i1(t)=Ifsin(ωt+θ+ϕ)+[i1(0)−Ifsin(θ+ϕ)]e−t/−tττi3(t)=i1(t)−i2(t)uOC(t)=αR3i3(t)+αL3di3(t)/di3(t)dtdtIf=Um/√(R1+αR3)2+ω2(L1+αL3)2 (2) 式中：ω为角频率；θ为故障初相角；ϕ为短路阻抗角；τ为直流衰减系数；i1(0)为短路时刻的i1值。
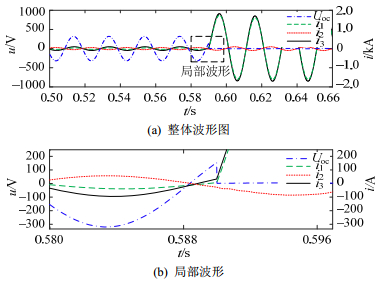
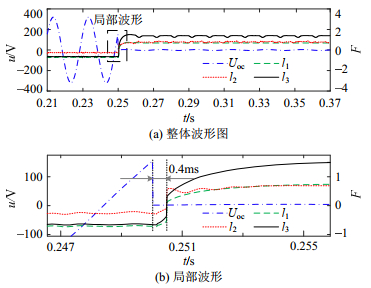
通过PSCAD仿真，可得A相短路时故障相的节点电压与各支路电流波形，如图 3所示。
![]()
图 3 F点单相短路时各支路电流与节点电压波形Figure 3. Waveform of each branch current and node voltage when single phase short circuit occurs at point F分析式(1)(2)与图 3可得：短路时，光伏输出电流具备PI环控制的响应特性；支路电流与节点电压均含有直流衰减分量，但低压交流系统的衰减系数较小，直流分量快速消减，短路电流、电压迅速进入稳态。此外，由于直流衰减分量初始值与故障初相角相关，短路时电流、电压突变强度随故障初相角呈正弦分布，故障特征离散度较高，不利于短路与正常工况的区分[21]。相较于短路的突变特征，周期分量的幅值与故障初相角解耦，用以表征短路时更稳定，更适合短路检测。
2. 改进最小二乘法的短路状态早期检测
2.1 瞬时幅值计算基本原理
考虑常规交流信号幅值求解所需数据的时间跨度较大，计算结果存在较大的时间滞后[25]，无法快速反应短路变化过程。为此，本文引入短路电流、电压向量，并通过模长计算求取采样信号的近似瞬时幅值。
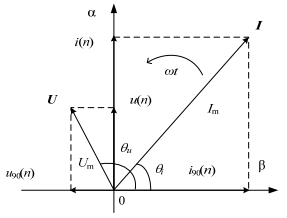
假设存在电流、电压采样信号为
{i(n)=Im⋅sin(100π⋅nTs+θi)u(n)=Um⋅sin(100π⋅nTs+θu) (3) 式中：n为采样点；Im、Um为电流、电压幅值；Ts为采样周期；θi、θu为电流、电压初相角。
将i、u投射到α-β直角坐标系的α轴上，并依此构造以100π角速度绕原点旋转的向量I和U，相量与α轴的起始夹角分别为θi、θu，存在向量I与向量U在β轴上的投影i90和u90，如图 4所示。
由图 4可得电流与电压瞬时幅值为
\left\{ \begin{array}{l} {I_{\text{m}}}(n) = \left| \mathit{\boldsymbol{I}} \right| = \sqrt {i{{(n)}^2} + {i_{90}}{{(n)}^2}} \hfill \\ {U_{\text{m}}}(n) = \left| \mathit{\boldsymbol{U}} \right| = \sqrt {u{{(n)}^2} + {u_{90}}{{(n)}^2}} \hfill \\ \end{array} \right. (4) 由此，可通过短路电流、电压离散信号及其90°偏转量快速计算短路电流、电压向量模长，并得出信号的瞬时幅值。
2.2 改进最小二乘拟合的幅值计算
为快速求解瞬时幅值，需先得到电流、电压的90°偏转信号i90、u90。由式(3)推导，易得i90、u90的离散化计算公式：
\left\{ \begin{array}{l} {i_{90}}(n) = {\text{d}}i(n)/{\text{d}}n/({\text{100}}{\mathsf{π}} \cdot {T_{\text{s}}}) \hfill \\ {u_{90}}(n) = {\text{d}}u(n)/{\text{d}}n/({\text{100}}{\mathsf{π}} \cdot {T_{\text{s}}}) \hfill \\ \end{array} \right. (5) 鉴于短路故障早期检测对瞬时幅值求解的快速性要求，采样频率一般设置较高。高频采样下，在保有短路快速变化特征的基础上确保算法的抗噪性，是本文瞬时幅值求解的难点。为此，本文通过最小二乘法对短时间窗内的采样数据进行直线拟合，既滤除噪声，又获得信号斜率，并可求得信号90°偏转量，便于幅值快速求解。
工程应用中，采样频率高，相较于工频信号周期T，采样滑动窗口对应的时间Δt较小，可近似为0。因此，极限公式可成立：
\mathop {{\text{lim}}}\limits_{\Delta t \to 0} {A_{\text{m}}}\sin (100{{\mathsf{π}}} \cdot \Delta t + \theta ) = {A_{\text{m}}}(100{{\mathsf{π}}} \cdot \Delta t + \theta ) (6) 式中Am为滑动窗口内数据对应的瞬时幅值。
式(6)说明短时间窗内工频信号采用直线拟合的合理性。进而，将第n个采样滑动窗口内的数据进行最小二乘直线拟合处理，可得直线参数为
\left\{ \begin{array}{l} k(n) = \frac{{N\sum {{x_i}{y_i}} - (\sum {{x_i}} )(\sum {{y_i}} )}}{{N\sum {x_i^2} - {{(\sum {{x_i}} )}^2}}} \hfill \\ b(n) = \frac{{(\sum {x_i^2} )(\sum {{y_i}} ) - (\sum {{x_i}} )(\sum {{x_i}{y_i}} )}}{{N\sum {x_i^2} - {{(\sum {{x_i}} )}^2}}} \hfill \\ \end{array} \right. (7) 式中：k(n)、b(n)为拟合直线的斜率与截距；i∈[1，2，…，m]，m为滑动窗口内数据个数；yi为滑动窗口中第i个采样值；xi表示第i个采样值的对应的时间。
考虑滑动窗口数据个数对直线拟合准确性和计算时间的影响，经实验测试，当采样频率为50kHz时，m取30时效果较好。
为进一步提高幅值计算的抗噪性，本文在首次直线拟合后，计算求得估计值 \hat y(i) 与原始数值的绝对误差数列，并挑选误差较小的原始数据，进行二次拟合，以提高最小二乘拟合的计算准确度。绝对误差数列为
\{ {d_1}, {d_2}, \cdots , {d_i}, {d_m}\} , {d_i} = |\hat y(i) - y(i)| (8) 本文通过k-means聚类算法实现绝对误差数列的挑选。由于仅需将绝对误差数列聚集为好与坏2类数据簇，因此，聚类的准则函数可定[26]为
{J_M}(H) = \sum\limits_i^m {\sum\limits_j^2 {{{({d_i} - {h_j})}^2}} } (9) 式中hj为聚类中心矩阵H中的元素。
该聚类算法共分为以下4个步骤：
1）依照类别数目初始化聚类中心。
2）通过比较样本与聚类中心hj的欧式距离，将样本分配至最近距离的中心点，以形成聚类簇。
3）计算各聚类簇内所有样本的平均值，并以此更替原有的聚类中心hj。
4）通过公式(9)判断误差是否收敛，若不收敛则重复第2步和第3步。
对于聚类结果，若两个聚类中心相距较远，则对聚类中心小的原始数据进行二次拟合，求得校正后的k’；若聚类中心数值较小且相距较近，则说明噪声影响较低，k’可取首次直线拟合值。
由于k’表征滑动窗口内数据的拟合斜率，为确保瞬时幅值计算时y0与y90的时序一致，需对瞬时幅值求解公式进行调整，即为
\left\{ \begin{array}{l} {y_0}(n) = \sum {\hat y(i)} /m \hfill \\ {y_{90}}(n) = k'/(100{{\mathsf{π}}} \cdot {T_{\text{s}}}) \hfill \\ {A_{\text{m}}}(n) = \sqrt {{y_0}{{(n)}^2} + {y_{90}}{{(n)}^2}} \hfill \\ \end{array} \right. (10) 考虑应用现场普遍存在高斯白噪声、脉冲噪声、谐波等干扰，为分析本文幅值计算的抗噪性，定义标准正弦信号：y(t)=100sin(100πt)，并通过matlab对信号分别施加高斯白噪声、0~0.2倍幅值的矩形脉冲噪声和三次谐波等干扰，对比文献[25]与本文幅值求解算法的计算误差，见表 1。
表 1 幅值快速求解误差分析Table 1. Error analysis for rapid solution of amplitude信号施加干扰 最大相对误差ηmax/% 干扰类型 参数 文献[25]
算法本文算法
(无k-means)本文算法
(含k-means)高斯白噪声
(SNR)60dB 4.36 0.60 0.59 40dB 80.59 2.54 2.10 脉冲噪声宽度 20μs 375.73 3.88 0.58 60μs 731.27 8.57 0.64 谐波畸变率
(含THD3)1.5% 4.50 3.51 3.53 2.5% 7.49 6.19 6.21 文献[25]所采用的快速计算方法虽对计算结果进行滑窗均值滤波处理，但在40dB信噪比的高斯噪声干扰下，最大相对误差高达80.59%。对于信号含有脉冲噪声的情况，文献[25]计算方法将彻底失效。本文采用最小二乘法计算幅值时，各类噪声干扰环境下的计算最大相对误差均较小。此外，对比实验结果表明，引入k-means算法可提高瞬时幅值的计算精度，尤其对脉冲噪声的抑制效果最为突出。值得一提的是，本文算法在谐波畸变下计算误差略高于其他干扰，但考虑短路时谐波源将被一同短路，谐波源对于短路电流、电压的影响可忽略不计。
2.3 短路状态早期检测判据
为提高短路检测判据的鲁棒性，避免大功率源-荷设备启停带来的干扰误判，本文在电流、电压瞬时幅值求解的基础上，构建短路状态早期检测的故障状态特征F(n)如下：
{F_i}(n) = {I_i}(n)/(\sqrt 2 {I_{{\text{f}}\min }}) - {U_i}(n)/(\sqrt 2 {U_N}) (11) 式中：Ii(n)、Ui(n)为第i个断路器检测的瞬时幅值；UN为额定电压有效值；Ifmin为保护点短路电流基准值，取该点所在线路末端短路下的电流稳态值，光伏并网断路器的Ifmin则为逆变器短路输出电流的有效值，一般为1.5倍额定电流[24]。
由式(11)可知：支路正常带载时，F(n)维持在–1附近；支路短路时，F(n)迅速增大为正值，且短路点越靠近线路首端，数值越大。以图 3仿真数据为例，各支路短路故征量如图 5所示。
![]()
图 5 F点短路时各支路故障状态特征Figure 5. Fault status characteristic of each branch when F point short circuit图 5中，不同类型支路的故障状态特征在F点发生短路故障的0.4 ms后一致响应。此外，由于F(n)中对瞬时电流、电压幅值进行标幺化处理，对于不同类型支路，F(n)具备较强的适应能力。因此，通过设置F(n)的阈值，可构建完整的短路状态早期检测判据，见式(12)、(13)。
{F_i}(n) \geqslant {F_{{\text{act}}.1}} (12) {F_i}(n) \geqslant {F_{{\text{act}}.2}}{{{\&}}}t \geqslant {t_{{\text{delay}}}} (13) 式中：Fact.1为速动阈值；Fact.2为短延时保护阈值；tdelay为短延时时间。
支路空载和短路下的F(n)约为–1和1，为确保正常停电不造成短路误判，短路状态早期检测阈值均需大于0。本文对大量短路实验数据进行分析，分析结果表明：各类型支路的速动阈值Fact.1取0.4时可确保短路可靠且快速检出；对于速动保护无法覆盖的长线路末端短路，当短延时保护阈值Fact.2取0.2时，则支路保护范围可延伸至下级支路，实现长线路短路保护全覆盖。配合短延时时间判据，源荷装置启动扰动均不造成短路误检，考虑断路器动作的固有时间，短延时时变判据tdelay可取20ms。
3. 节点自治的短路保护方法
3.1 多节点区域保护系统技术概念
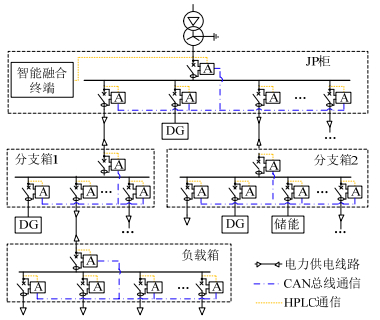
为满足含分布式电源低压交流系统短路保护的选择性，本文短路状态早期检测的基础上，提出多节点区域保护系统技术概念，如图 6所示。
图 6中，多节点区域保护系统由各断路器的智能保护模块与台区智能融合终端组成，模块A为断路器装配的智能保护装置，该装置具备CAN总线与HPLC通信接口。智能融合终端可根据台区运行状态进行断路器阈值优化，并通过HPLC通信更新各断路器的保护参数，完善各节点间的保护选择性。同时，为满足分布式电源接入下同节点各断路器的保护选择性要求，本文采用节点区域CAN总线通信，实现同一节点断路器的短路信息共享，并设计基于多信息分析的断路器保护决策机制，以构建节点内区域自治、节点间协调配置的短路快速保护方案。此外，在布置多节点区域保护系统的同时，保留现有低压交流保护方法作为本文所提保护方法的后备保护。
需指出，HPLC通信负责对全局智能保护装置的保护阈值管理，不参与短路保护的决策过程。区域CAN总线通信配置在柜/箱内，通信距离短，且柜/箱壳体接地形成屏蔽，对外部辐射干扰的抵抗能力较强。此外，CAN总线通信具备数据丢失重传机制，可确保短路信息传输的可靠性。
3.2 节点自治的保护决策机制
由于2.3节构建的短路早期检测判据包含标幺化后的短路电流、电压信息，对于不同箱/柜间的断路器，其保护响应已具备较为良好的选择性。但对于同一柜/箱内的断路器，其电气距离相近，当短路点位于出线处，极易造成断路器越级跳闸。为此，本文提出基于短路电流极性相关原理的个体选择性诊断方法。
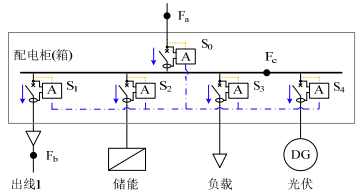
以某一柜/箱为例，按照短路点与母线节点的电气关系，可将短路位置分为进线侧、出线侧与母线3种类型。断路器则可分为上级断路器(S0)与下级断路器(S1、S2、S3、S4)，如图 7所示。
![]()
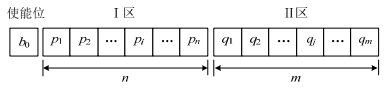
图 7 配电柜不同短路位置示意图Figure 7. Schematic diagram of different short circuit positions of distribution cabinet规定各断路器电流正方向如图 7箭头所示。系统发生短路故障后，检出短路的断路器迅速向总线发送该时刻电流极性。各断路器接收其他断路器的电流极性信息后与自身进行对比，两者电流极性相同时，极性相关系数为1，不同则为0。获得极性相关系数后，存入MCU的极性相关度缓存区。缓存区结构如图 8所示。
图 8中：使能位b0用以表征自身断路器是否检出短路，检出为1，未检出为0，使能位为1时，缓存区数据生效；Ⅰ区用以存放本断路器与上级断路器的极性相关系数pi；Ⅱ区用以存放本断路器与下级断路器的极性相关系数qj。极性相关度缓存区自首信息写入，10 ms后复位并清空所有信息，以备新一轮的保护决策。
为提高保护决策效率，设定各断路器满足b0为1，且CAN总线持续空闲超过0.2ms，便进行个体保护决策判定。其中，上、下级断路器动作判定条件SⅠ、SⅡ别为式(14)(15)：
{S}_{\mathrm{Ⅰ}}=\left\{ \begin{array}{l} 1, m=0\\ 1\oplus {q}_{1}, m=1\\ f({q}_{1}, {q}_{2}, \cdots , {q}_{m}), m\ge 2\end{array} \right. (14) {S}_{\mathrm{Ⅱ}}=\left\{ \begin{array}{l}1, m=0或n=0\\ ({p}_{1}\text{||}\cdots \text{||}{p}_{n})\oplus f(1, {q}_{1}, \cdots , {q}_{m}), m\ge 1且n\ge 1\end{array} \right. (15) 式中：定义函数f，自变量全部相同时输出1，其余情况则输出0； \oplus 为异或运算符；||为或运算。
通过上述决策流程可知，节点自治的保护决策无需设置主站，各断路器的智能保护装置可根据CAN总线信息自行决策。当短路回路上非故障支路的电流信息丢失时，并不会对保护决策结果产生影响；当短路所在支路的电流信息丢失时，由于缺乏短路支路信息，各智能保护装置短路电流极性相关度缓存区内信息与母线短路时相似，将触发母线短路保护，仍可切除短路点。
为说明本文所提保护决策机制的正确性，以图 7配电箱电气拓扑为例，分析Fa、Fb、Fc点短路时，各断路器动作判定的准确性。测试结果如表 2所示，其中储能设备为电源模式。
表 2 各断路器动作判定情况Table 2. Action judgment of each circuit breaker短路点 断路器 电流极性相关度缓存区 SⅠ/SⅡ输出 使能位 Ⅰ区 Ⅱ区 Fa S0 0 - - - S1 0 - - - S2 1 × {1} 1 S3 0 - - - S4 1 × {1} 1 Fb S0 1 × {1, 0, 0} 0 S1 1 1 {0, 0} 1 S2 1 0 {0, 1} 0 S3 0 - - - S4 1 0 {0, 1} 0 Fc S0 1 × {0, 0} 1 S1 0 - - - S2 1 0 {1} 1 S3 0 - - - S4 1 0 {1} 1 由表 2可知，当Fa短路时，由于逆变器限制输出，流经S0的短路电流较小，S0无响应，经由S2、S4动作判定，断开分布式电源；当Fb短路时，S1动作判定；Fc当短路时，S0、S2、S4均动作判定。若储能设备充电状态时发生短路，S2使能位为0，该支路无需响应。由此可见，本文提出的保护决策机制适用于含分布式电源低压交流系统，并对储能源荷工况转换具有较高兼容性。
4. 含分布式光伏低压交流系统保护实验
4.1 真型实验系统介绍
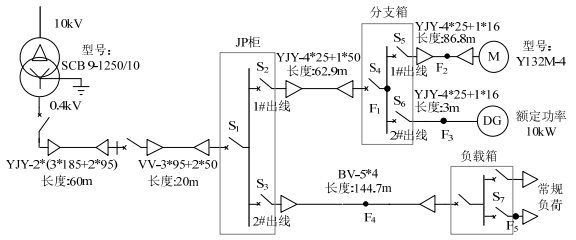
为验证本文所提保护方法的有效性，在多层级低压交流真型实验系统上进行短路检测及其选择性保护实验验证，实验系统一次线路见图 9。
多层级低压交流系统真型实验系统现场，如图 10所示。本文将所研制的智能保护模块样机接入真型实验系统中，并通过NI Compact-RIO搭建短路保护录波平台，录制实验过程中的短路电流、电压信号与智能保护模块装置状态引脚波形。结合短路过程的装置样机响应结果，对短路保护过程的特征量进行复现分析。
实验系统具备10 kW单相光伏、7.5 kW三相异步电动机与大功率负载，配备JP柜、分支箱与负载箱，各断路器保护模块电流、电压采样频率为50 kHz。根据2.3节，可由线路参数快速计算各断路器的Ifmin值，见表 3。
表 3 各断路器Ifmin取值表Table 3. Ifmin value table of each circuit breaker编号 安装位置 Ifmin/A 编号 安装位置 Ifmin/A S1 JP柜进线端 2902 S5 分支箱1#出线 643 S2 JP柜1#出线 1228 S6 分支箱2#出线 60 S3 JP柜2#出线 223 S7 负载箱出线 280 S4 分支箱进线端 1228 — — — 4.2 短路检测早期性分析
为阐述本文所提短路状态早期检测的优势，将传统规格断路器(ABB SECA1 125A/400V)接入S5，并通过短路实验进行验证(故障初相角取0~180°)。对比电流速动保护与本文检测方法的检测性能，定义短路检出前最大电流峰值即为检测期间的冲击电流。其中，F2点单相短路下稳态电流峰值约为1800 A，检测结果如表 4所示。
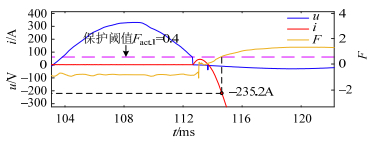
表 4 S5短路检测结果对比Table 4. Comparison of short-circuit detection results in S4故障初相角α/(°) 电流速动保护 本文检测方法 检测用时t/ms 冲击电流i/A 检测用时t/ms 冲击电流i/A 10.8 4.8 1673.2 0.92 256.9 30.6 4.7 1790.0 0.44 265.6 50.4 4.2 1735.0 0.50 373.6 70.2 4.0 1572.0 0.50 421.6 91.8 4.0 1327.0 0.48 441.2 111.6 4.7 996.1 0.48 323.1 131.4 9.0 –1774.0 0.48 311.5 151.2 7.8 –1790.0 0.56 220.6 172.5 6.5 –1784.0 2.00 –235.2 由表 4可知，本文短路检测方法在全范围故障初相角下，检测用时约0.5 ms。本文方法短路检测期间，冲击电流均远小于电流速动保护。其中，故障初相角在172.5°附近，本文方法检测用时明显增加，可达2.00 ms，分析该故障初相角下短路发展情况，如图 11所示。
图 11中，短路发生后，电流出现首个波峰，此时电流峰值尚小。随后，当电流发展至–235.2 A，状态特征量F增大并触发保护，相较于短路稳态峰值，此时短路电流仍处在发展阶段，短路检测仍具有早期性优势。
4.3 低压光伏保护适用性分析
4.3.1 光伏支路保护快速性分析
为验证本文所提方法对分布式光伏的适用性，本文以F1点短路故障为例，对比光伏逆变器主动式保护和本文方法的检测效果，实验结果见表 5。其中，光伏逆变器采用电流瞬时值越限触发机制，保护阈值一般定为2倍额定输出电流，电流采样以母线向光伏为参考正方向。
表 5 光伏支路检测结果对比Table 5. Comparison of DG branch detection results故障初相角α/(°) 逆变器短路电流保护 本文短路检测方法 检测用时t/ms 检出电流i/A 检测用时t/ms 检出电流i/A 11.2 4.50 –90.0 0.46 –23.7 31.7 3.38 –90.2 0.44 –46.4 53.3 2.40 –90.1 0.44 –64.7 73.4 11.08 90.1 0.44 –71.8 91.8 9.80 90.0 0.42 –72.5 113.4 8.36 90.0 0.42 –62.3 131.8 7.48 90.1 0.42 –47.3 151.2 6.72 90.1 0.42 –25.5 175.7 5.40 90.2 0.42 6.9 表 5中，光伏支路采用本文方法时，全范围故障初相角的短路检测用时均不超过0.50 ms。相较于光伏逆变器的主动式保护，本文短路检测方法用时更短，短路检出时，逆变器输出电流尚小，可为后续选择性保护分断创造条件，更有利于提高逆变器的使用寿命。
对比表 4，大部分短路故障初相角下，光伏支路与普通支路检测用时相近。但在故障初相角接近0°或180°时，光伏支路的检测较普通支路更快。这是由于光伏逆变器输出惯性较小，即使在0°或180°故障初相角附近的短路，输出电流也可迅速响应。
由此可见，光伏支路与普通支路的短路检测存在一定的时间极差。为提高选择性保护的可靠性，规定光伏支路在检出短路后，仍需在一定时间内等待普通支路的检测信息，再进行选择性保护响应决策，以避免因检测时间先后差异而造成的误判。参考表 4与表 5，两类支路短路检测最大时间差约为1.5 ms，在留有裕度的情况下，本文设置持续监测时间为2.0 ms。
4.3.2 光伏电源出力对保护的影响
现场受光照强度的影响，光伏电源的最大出力不确定性高。为验证本文所提方法对光伏电源不同出力下短路保护的适应性，考虑真型实验系统难以灵活调整光照强度，本文根据真型实验系统搭建仿真系统，采用的三相光伏器额定功率取为30 kw，并通过仿真的得到光照强度分别为50、200、800、1000 W/m2下并网点三相短路故障检测结果，如表 6所示。
表 6 光伏电源出力对短路检测的影响Table 6. Influence of photovoltaic power output on short circuit detection光照强度/(W/m2) 短路电流I/A 最大特征值Fmax 检测用时t/ms 1000 70.8 0.929 0.34 800 70.8 0.905 0.40 200 70.7 0.836 0.44 50 58.6 0.710 1.14 由表 6可知，当光照强度超过一定值后(本文为200 W/m2)，光伏短路电流与额定光照时基本一致，该现象与文献4研究结论一致。此时，最大短路特征均在0.8以上，短路后0.50 ms内可完成检测。当光照强度很小时，光伏短路输出电流显著减小，该情况下本文方法仍可实现短路检测。以光照50 W/m2为例，此时最大短路特征为0.710，短路检测用时1.14 ms。若光伏电源配置储能，输出短路电流则与光照无关。由此可见，本文所提方法可适用于光伏电源不同出力工况。
4.4 保护方法可靠性分析
4.4.1 运行工况扰动的鲁棒性
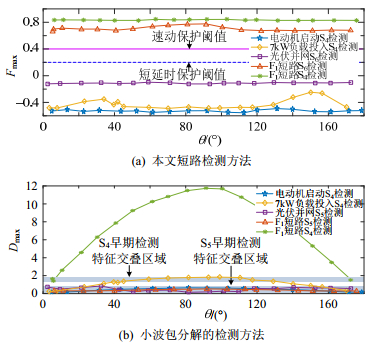
为阐述本文所提保护方法在有源低压交流系统复杂运行工况下的鲁棒性，分析阻性负荷满载投入、异步电动机直接启动、分布式电源满发并网等工况对短路检测特征的影响，本文复现文献[27]所采用的基于小波包分解的短路早期检测方法，选取小波分解第四层细节分量的二次细节分量D作为检测特征。本文以F1点全范围故障初相角下的单相短路故障为例，进行对比实验分析，信号采样频率统一设为50 kHz。记录两种检测方法在不同初相角下源荷装置接入与短路故障的最大短路特征量Fmax、Dmax，如图 12所示。
![]()
图 12 源荷装置启动的最大短路特征扰动Figure 12. Maximum short-circuit characteristic disturbance of source or load device start-up由图 12(a)可知，各类源荷装置启动下的短路状态早期检测特征分布集中，且与速动保护、短延时保护阈值存在明显差距，保护不易误动。图 12(b)中，非光伏并网支路的短路小波细节分量Dmax数值波动较大，但数值均在电动机启动的Dmax上方。故障初相角0°/180°时，Dmax约为1.5，而阻性负荷启动的扰动特征高达1.834，因而，短路与阻性负荷启动的特征值存在交叠区域，难以配置检测阈值，保护误动或拒动风险较大。此外，光伏支路在并网与短路下，Dmax的交叠区域更大，这意味小波包分解的检测方法将完全失效。由此可见，本文所提保护方法相较于小波算法具备更强的鲁棒性。
4.4.2 短路保护方法的对比分析
为验证所提保护方法的技术优势，随机抽取源荷投切与短路工况进行实验，并对比所提保护方法与小波算法的短路检测效果，实验时刻以A相电压相角为准。考虑低压交流系统短路故障的过渡电阻主要由导体接触电阻构成，一般为0~0.2 Ω，设置低压交流短路的过渡电阻为0.01~0.32 Ω。其中，小波算法的检测阈值依照文献[27]规则设置，S7处取2.00，S6取0.30。检测结果见表 7。
表 7 短路保护方法的检测结果对比Table 7. Comparison of detection results of short-circuit protection methods实验信息 本文方法 小波变换 类型 电压初相角 过渡电阻 检测结果 Fmax 检测结果 Dmax 纯阻性负载投切
(S7检测)38.9° - 正常 –0.43 正常 1.78 93.6° - 正常 –0.29 短路 2.68 129° - 正常 –0.45 短路 2.05 F5短路
(S7检测)10.8° 0.02Ω 短路 1.05 短路 2.41 148° 0.22Ω 短路 0.99 短路 4.95 171° 0.32Ω 短路 0.96 正常 1.31 光伏并网
(S6检测)21.4° - 正常 –0.04 短路 0.75 59.0° - 正常 –0.04 短路 0.40 141° - 正常 –0.04 短路 0.44 F1短路
(S6检测)34.0° 0.01Ω 短路 0.93 短路 0.33 153° 0.21Ω 短路 0.78 短路 0.35 164° 0.31Ω 短路 0.76 正常 0.19 表 7中，采用小波分解的短路早期检测算法在电压相角93.6°时投入纯阻性负载，S7检测最大D达2.68，超过故障初相角10.8°下的最大D，阻性负载投切工况将造成小波算法的误检。此外，由于光伏并网和光伏输出侧短路的最大D数值接近，导致小波算法误检和漏检，无法适用分布式电源支路。而本文所提保护方法均能准确辨识是否发生短路。电压相角93.6°时投入纯阻性负载，最大扰动不超过–0.29，对于光伏并网接入，最大扰动不超过–0.04，且由于投切扰动持续时间短，不易造成误检。对于不同过渡电阻的短路，本文保护方法检测的短路特征值均保持在较高数值。因此，可忽略不同短路过渡电阻对本文所提保护方法的影响。由此可见，相较于采用小波算法的短路早期检测方法，所提短路快速保护方法的可靠性更高。
4.5 保护方法的选择性分析
4.5.1 跨节点保护范围适配分析
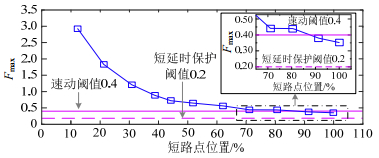
为分析本文保护方法对于上下级节点的适配度，以JP柜2#线路为例，短路点依次设于线路不同位置，分析S3检测的特征量与短路点位置的关系。故障初相角设为90°，记录各短路位置下最大短路特征，如图 13所示。
![]()
图 13 短路特征与短路位置关系Figure 13. Relationship between short circuit characteristics and short circuit position图 13中，当短路点位于线路86%内，S3速动保护均可触发；当短路点位于线路86%后，短延时保护将发挥作用，且S3的短延时保护范围仍可向下级线路延伸。因此，对于不同层级断路器，本文保护方法具备良好的适配能力。
4.5.2 节点自治的保护选择性实验
为验证节点内各支路保护的选择性，本文以分支箱为实验对象，设置母线(F1)、负载支路(F2)和光伏支路(F3)共三处短路，测试各支路保护响应情况，以短路时刻到断路器分断触发时间为保护出口时延，实验结果见表 8。
表 8 各支路保护选择性实验结果Table 8. Experimental results of protection selectivity of each branch短路点 故障初相角α/(°) 保护触发对象 保护出口时延t/ms F1 31.5 S4/S6 1.24 / 1.23 91.7 S4/S6 0.84 / 0.84 151.1 S4/S6 4.12 / 2.40 F2 30.8 S5 0.73 91.8 S5 0.74 151.2 S5 0.78 F3 32.0 S6 1.14 91.5 S6 0.77 150.6 S6 2.42 由表 8可知，不同位置发生短路时，各断路器均能准确响应，且断路器保护出口时延约为1 ms，此时短路电流首个波峰尚未抵达，有利于短路电流快速分断。当故障初相角接近180°时，上级支路断路器S4检测用时较长，致使保护出口时延较长。该情况下，短路电流虽然有机会到达首个波峰，但此时电流峰值较小，短路仍处于发展早期，同样有利于短路电流分断。
上述实验结果可知，本文所提短路快速保护方法的保护出口时间大部分维持在1.00 ms以内，明显快于现有保护方法，可在现有低压保护方法响应前触发对应断路器保护分闸。
5. 结论
本文针对含分布式光伏低压交流系统短路保护面临的选择性难题，提出节点自治的短路快速保护方案，且取得成果如下：
1）本文所提基于改进最小二乘法的短路状态早期检测方法，对于低压交流系统常规支路、分布式电源支路和储能支路的短路故障，均可在故障0.50 ms内完成辨识。
2）提出基于支路短路电流极性相关系数的保护决策机制，对于含源荷接入的电气节点，可在短路发生1.00 ms左右完成各支路保护决策及其故障支路分断触发，克服低压交流系统多源拓扑下的保护选择性难题。
3）通过真型实验系统验证了本文所提保护方法的早期性、可靠性性与选择性，为研究有源低压交流系统选择性保护提供理论基础，研究成果具有一定的工程参考价值。
本文将在多节点区域保护系统技术的基础上，继续开展有源低压交流系统各支路保护单元保护阈值多目标优化方面的研究工作，完善短路保护系统的全局选择性。
-
![]()
图 1 含分布式光伏低压交流系统拓扑图
Figure 1. Topology of the low-voltage AC system with distributed photovoltaic
![]()
图 2 含分布式光伏低压交流系统单相短路简化模型
Figure 2. Simplified model of single-phase short circuit in low-voltage AC system with distributed photovoltaic
![]()
图 3 F点单相短路时各支路电流与节点电压波形
Figure 3. Waveform of each branch current and node voltage when single phase short circuit occurs at point F
![]()
图 5 F点短路时各支路故障状态特征
Figure 5. Fault status characteristic of each branch when F point short circuit
![]()
图 7 配电柜不同短路位置示意图
Figure 7. Schematic diagram of different short circuit positions of distribution cabinet
![]()
图 12 源荷装置启动的最大短路特征扰动
Figure 12. Maximum short-circuit characteristic disturbance of source or load device start-up
![]()
图 13 短路特征与短路位置关系
Figure 13. Relationship between short circuit characteristics and short circuit position
表 1 幅值快速求解误差分析
Table 1 Error analysis for rapid solution of amplitude
信号施加干扰 最大相对误差ηmax/% 干扰类型 参数 文献[25]
算法本文算法
(无k-means)本文算法
(含k-means)高斯白噪声
(SNR)60dB 4.36 0.60 0.59 40dB 80.59 2.54 2.10 脉冲噪声宽度 20μs 375.73 3.88 0.58 60μs 731.27 8.57 0.64 谐波畸变率
(含THD3)1.5% 4.50 3.51 3.53 2.5% 7.49 6.19 6.21 
下载: 导出CSV
表 2 各断路器动作判定情况
Table 2 Action judgment of each circuit breaker
短路点 断路器 电流极性相关度缓存区 SⅠ/SⅡ输出 使能位 Ⅰ区 Ⅱ区 Fa S0 0 - - - S1 0 - - - S2 1 × {1} 1 S3 0 - - - S4 1 × {1} 1 Fb S0 1 × {1, 0, 0} 0 S1 1 1 {0, 0} 1 S2 1 0 {0, 1} 0 S3 0 - - - S4 1 0 {0, 1} 0 Fc S0 1 × {0, 0} 1 S1 0 - - - S2 1 0 {1} 1 S3 0 - - - S4 1 0 {1} 1
下载: 导出CSV
表 3 各断路器Ifmin取值表
Table 3 Ifmin value table of each circuit breaker
编号 安装位置 Ifmin/A 编号 安装位置 Ifmin/A S1 JP柜进线端 2902 S5 分支箱1#出线 643 S2 JP柜1#出线 1228 S6 分支箱2#出线 60 S3 JP柜2#出线 223 S7 负载箱出线 280 S4 分支箱进线端 1228 — — —
下载: 导出CSV
表 4 S5短路检测结果对比
Table 4 Comparison of short-circuit detection results in S4
故障初相角α/(°) 电流速动保护 本文检测方法 检测用时t/ms 冲击电流i/A 检测用时t/ms 冲击电流i/A 10.8 4.8 1673.2 0.92 256.9 30.6 4.7 1790.0 0.44 265.6 50.4 4.2 1735.0 0.50 373.6 70.2 4.0 1572.0 0.50 421.6 91.8 4.0 1327.0 0.48 441.2 111.6 4.7 996.1 0.48 323.1 131.4 9.0 –1774.0 0.48 311.5 151.2 7.8 –1790.0 0.56 220.6 172.5 6.5 –1784.0 2.00 –235.2
下载: 导出CSV
表 5 光伏支路检测结果对比
Table 5 Comparison of DG branch detection results
故障初相角α/(°) 逆变器短路电流保护 本文短路检测方法 检测用时t/ms 检出电流i/A 检测用时t/ms 检出电流i/A 11.2 4.50 –90.0 0.46 –23.7 31.7 3.38 –90.2 0.44 –46.4 53.3 2.40 –90.1 0.44 –64.7 73.4 11.08 90.1 0.44 –71.8 91.8 9.80 90.0 0.42 –72.5 113.4 8.36 90.0 0.42 –62.3 131.8 7.48 90.1 0.42 –47.3 151.2 6.72 90.1 0.42 –25.5 175.7 5.40 90.2 0.42 6.9
下载: 导出CSV
表 6 光伏电源出力对短路检测的影响
Table 6 Influence of photovoltaic power output on short circuit detection
光照强度/(W/m2) 短路电流I/A 最大特征值Fmax 检测用时t/ms 1000 70.8 0.929 0.34 800 70.8 0.905 0.40 200 70.7 0.836 0.44 50 58.6 0.710 1.14
下载: 导出CSV
表 7 短路保护方法的检测结果对比
Table 7 Comparison of detection results of short-circuit protection methods
实验信息 本文方法 小波变换 类型 电压初相角 过渡电阻 检测结果 Fmax 检测结果 Dmax 纯阻性负载投切
(S7检测)38.9° - 正常 –0.43 正常 1.78 93.6° - 正常 –0.29 短路 2.68 129° - 正常 –0.45 短路 2.05 F5短路
(S7检测)10.8° 0.02Ω 短路 1.05 短路 2.41 148° 0.22Ω 短路 0.99 短路 4.95 171° 0.32Ω 短路 0.96 正常 1.31 光伏并网
(S6检测)21.4° - 正常 –0.04 短路 0.75 59.0° - 正常 –0.04 短路 0.40 141° - 正常 –0.04 短路 0.44 F1短路
(S6检测)34.0° 0.01Ω 短路 0.93 短路 0.33 153° 0.21Ω 短路 0.78 短路 0.35 164° 0.31Ω 短路 0.76 正常 0.19
下载: 导出CSV
表 8 各支路保护选择性实验结果
Table 8 Experimental results of protection selectivity of each branch
短路点 故障初相角α/(°) 保护触发对象 保护出口时延t/ms F1 31.5 S4/S6 1.24 / 1.23 91.7 S4/S6 0.84 / 0.84 151.1 S4/S6 4.12 / 2.40 F2 30.8 S5 0.73 91.8 S5 0.74 151.2 S5 0.78 F3 32.0 S6 1.14 91.5 S6 0.77 150.6 S6 2.42
下载: 导出CSV
-
[1] 刘芳, 刘威, 汪浩东, 等. 高比例新能源电力系统振荡机理及其分析方法研究综述[J]. 高电压技术, 2022, 48(1): 95-113. LIU Fang, LIU Wei, WANG Haodong, et al. Review on oscillation mechanism and analysis methods of high proportion renewable energy power system[J]. High Voltage Engineering, 2022, 48(1): 95-113(in Chinese).
[2] 李建林, 郭兆东, 马速良, 等. 新型电力系统下"源网荷储"架构与评估体系综述[J]. 高电压技术, 2022, 48(11): 4330-4341. LI Jianlin, GUO Zhaodong, MA Suliang, et al. Overview of the "source-grid-load-storage" architecture and evaluation system under the new power system[J]. High Voltage Engineering, 2022, 48(11): 4330-4341(in Chinese).
[3] 韩民晓, 范溢文, 刘金峻, 等. 换流器型电网的理念与探索[J]. 电网技术, 2023, 47(2): 539-552. DOI: 10.13335/j.1000-3673.pst.2022.1108 HAN Minxiao, FAN Yiwen, LIU Jinjun, et al. Concept and practice of converter-based grid[J]. Power System Technology, 2023, 47(2): 539-552(in Chinese). DOI: 10.13335/j.1000-3673.pst.2022.1108
[4] 李建林, 谭宇良, 王含, 等. 配网及光储微网储能系统配置优化策略[J]. 高电压技术, 2022, 48(5): 1893-1902. LI Jianlin, TAN Yuliang, WANG Han, et al. Research on configuration optimization of energy storage system in distribution network and optical storage microgrid[J]. High Voltage Engineering, 2022, 48(5): 1893-1902(in Chinese).
[5] 和敬涵, 王语然, 李猛, 等. 基于电流波形畸变特征的高比例光伏配电网故障方向判别原理[J]. 电网技术, 2023, 47(12): 4856-4865. DOI: 10.13335/j.1000-3673.pst.2023.1365 HE Jinghan, WANG Yuran, LI Meng, et al. New Fault direction identification based on current distortion characteristics in high proportion PV distribution system[J]. Power System Technology, 2023, 47(12): 4856-4865(in Chinese). DOI: 10.13335/j.1000-3673.pst.2023.1365
[6] 刘健, 林涛, 同向前, 等. 分布式光伏电源对配电网短路电流影响的仿真分析[J]. 电网技术, 2013, 37(8): 2080-2085. http://www.dwjs.com.cn/uB2dYBnbZLTGoOcEvyUaRbM0h2FFf4XNzNuy22d208A%3D?encrypt=1 LIU Jian, LIN Tao, TONG Xiangqian, et al. Simulation analysis on influences of distributed photovoltaic generation on short-circuit current in distribution network[J]. Power System Technology, 2013, 37(8): 2080-2085(in Chinese). http://www.dwjs.com.cn/uB2dYBnbZLTGoOcEvyUaRbM0h2FFf4XNzNuy22d208A%3D?encrypt=1
[7] 吴成国, 肖仕武. 高比例分布式电源接入电网短路电流的拟牛顿迭代计算方法[J]. 电网技术, 2022, 46(12): 4581-4590. DOI: 10.13335/j.1000-3673.pst.2022.1357 WU Chengguo, XIAO Shiwu. Quasi-Newton iterative calculation method for short circuit current of high proportion distributed generation connected to power grid[J]. Power System Technology, 2022, 46(12): 4581-4590(in Chinese). DOI: 10.13335/j.1000-3673.pst.2022.1357
[8] 袁智勇, 徐全, 徐刚, 等. 含大容量分布式电源接入的配电网电流保护优化方案[J]. 电网技术, 2021, 45(5): 1862-1869. DOI: 10.13335/j.1000-3673.pst.2020.0230a YUAN Zhiyong, XU Quan, XU Gang, et al. Current protection optimization scheme in distribution network with large capacity distributed generators[J]. Power System Technology, 2021, 45(5): 1862-1869(in Chinese). DOI: 10.13335/j.1000-3673.pst.2020.0230a
[9] El-HAMRAWY A H, EBRAHIEM A A M, MEGAHED A I. Improved adaptive protection scheme based combined centralized/ decentralized communications for power systems equipped with distributed generation[J]. IEEE Access, 2022, 10: 97061-97074. DOI: 10.1109/ACCESS.2022.3205312
[10] 陈宏山, 徐舒, 李正红, 等. 计及5G通信异常工况的有源配电网快速综合保护方案[J]. 电力系统保护与控制, 2021, 49(15): 159-168. CHEN Hongshan, XU Shu, LI Zhenghong, et al. A new fast comprehensive protection scheme of an active distribution network considering the abnormal operating conditions of 5G communication[J]. Power System Protection and Control, 2021, 49(15): 159-168(in Chinese).
[11] REIZ C, LEITE J B. Optimal coordination of protection devices in distribution networks with distributed energy resources and microgrids[J]. IEEE Access, 2022, 10: 99584-99594. DOI: 10.1109/ACCESS.2022.3203713
[12] 曾德辉, 王钢, 郭敬梅, 等. 含逆变型分布式电源配电网自适应电流速断保护方案[J]. 电力系统自动化, 2017, 41(12): 86-92. ZENG Dehui, WANG Gang, Guo Jingmei, et al. Adaptive current protection scheme for distribution network with inverter-interfaced distributed generators[J]. Automation of Electric Power Systems, 2017, 41(12): 86-92(in Chinese).
[13] 乔一达, 吴红斌, 吴通华, 等. 含逆变型分布式电源的配电网分区域电流保护[J]. 电工技术学报, 2022, 37(S1): 134-144. QIAO Yida, WU Hongbin, WU Tonghua, et al. A partitioned current protection scheme of distribution network with inverter interfaced distributed generator[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 134-144(in Chinese).
[14] 何思名, 袁智勇, 雷金勇, 等. 基于改进灰狼算法的DG接入配电网反时限过电流保护定值优化[J]. 电力系统保护与控制, 2021, 49(18): 173-181. HE Siming, YUAN Zhiyong, LEI Jinyong, et al. Optimal setting method of inverse time over-current protection for a distribution network based on the improved grey wolf optimization[J]. Power System Protection and Control, 2021, 49(18): 173-181(in Chinese).
[15] HUANG Liang, WU Chao, ZHOU Dao, et al. A power-angle-based adaptive overcurrent protection scheme for grid-forming inverter under large grid disturbances[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 5927-5936. DOI: 10.1109/TIE.2022.3199906
[16] 李振兴, 田斌, 尹项根, 等. 含分布式电源与随机负荷的主动配电网保护[J]. 高电压技术, 2017, 43(04): 1231-1238. LI Zhenxing, TIAN Bin, YIN Xianggen, et al. Overview on active distribution network relaying protective containing distributed resources and stochastic load[J]. High Voltage Engineering, 2017, 43(4): 1231-1238(in Chinese).
[17] 中华人民共和国住房和城乡建设部. 光伏发电站设计规范: GB 50797-2012[S]. 北京: 中国计划出版社, 2012. [18] 梁营玉, 卢正杰. 基于补偿系数的有源配电网自适应电流差动保护[J]. 电网技术, 2022, 46(6): 2268-2275. DOI: 10.13335/j.1000-3673.pst.2021.0792 LIANG Yingyu, LU Zhengjie. Adaptive differential protection principle based on compensation coefficient for active distribution network[J]. Power System Technology, 2022, 46(6): 2268-2275(in Chinese). DOI: 10.13335/j.1000-3673.pst.2021.0792
[19] 徐萌, 邹贵彬, 高磊, 等. 含逆变型分布式电源的配电网正序阻抗纵联保护[J]. 电力系统自动化, 2017, 41(12): 93-99. XU Meng, ZOU Guibin, GAO Lei, et al. Pilot protection of positive sequence impedance for distribution network with inverter-based distributed generator[J]. Automation of Electric Power Systems, 2017, 41(12): 93-99(in Chinese).
[20] 晁晨栩, 郑晓冬, 高飘, 等. 含高比例光伏配电网的高频阻抗差动保护[J]. 中国电机工程学报, 2021, 41(20): 6968-6978. CHAO Chenxu, ZHENG Xiaodong, GAO Piao, et al. High frequency impedance differential protection with high proportion of photovoltaic power distribution network[J]. Proceedings of the CSEE, 2021, 41(20): 6968-6978(in Chinese).
[21] MAO Chunxiang, WEI Peng, LIU Ruopeng, et al. Line pilot protection of flexible DC grid based on traveling-wave JS divergence[J]. IEEE Access, 2022, 10: 129269-129278. DOI: 10.1109/ACCESS.2022.3227961
[22] 缪希仁, 吴晓梅. 低压系统多层级短路电流早期检测与预测[J]. 电工技术学报, 2014, 29(11): 177-183. MIAO Xiren, WU Xiaomei. Early detection and prediction for short-circuit current in a multi-level low voltage system[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 177-183(in Chinese).
[23] 韩博文, 王钢, 李海锋, 等. 含逆变型分布式电源配电网的新型纵联保护方案[J]. 高电压技术, 2017, 43(10): 3453-3462. HAN Bowen, WANG Gang, LI Haifeng, et al. Novel pilot protection scheme for distribution networks with inverter-interfaced distributed generators[J]. High Voltage Engineering, 2017, 43(10): 3453-3462(in Chinese).
[24] CHAKRABORTY S, KROPOSKI B, KRAMER W. Advanced power electronic interfaces for distributed energy systems part 2: modeling, development, and experimental evaluation of advanced control functions for single-phase utility-connected inverter[R]. Golden, Colorado, US: National Renewable Energy Laboratory, 2008.
[25] 吴浩伟, 周樑, 孙朝晖, 等. 电力系统短路故障快速检测方案研究[J]. 电力系统保护与控制, 2010, 38(24): 88-92. WU Haowei, ZHOU Liang, SUN Zhaohui, et al. Study on fast detecting scheme of power system short-circuit fault[J]. Power System Protection and Control, 2010, 38(24): 88-92(in Chinese).
[26] YAO Gang, WU Yang, HUANG Xiaoxu, et al. Clustering of typical wind power scenarios based on k-means clustering algorithm and improved artificial bee colony algorithm[J]. IEEE Access, 2022, 10: 98752-98760.
[27] 吴晓梅, 缪希仁. 低压系统多层级短路故障早期检测辨识研究[J]. 电工电能新技术, 2015, 34(9): 38-43. WU Xiaonei, MIAO Xiren. Research on early detection of short-circuit fault in multi-level low voltage system[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(9): 38-43(in Chinese).
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
下载:
