MMC-HVDC双极故障条件下自适应限流控制策略

王硕; 何柏娜; 程婷; 张东进; 代维汉; 尉元龙

doi:10.12158/j.2096-3203.2024.06.006

MMC-HVDC双极故障条件下自适应限流控制策略

1.
山东理工大学电气与电子工程学院, 山东淄博 255000
2.
国网电力科学研究院武汉南瑞有限责任公司, 湖北武汉 430077

基金项目:

山东省自然科学基金资助项目“交直流混联架空输电线路放电特性及灭弧方案研究” ZR2021ME057

详细信息

作者简介:
王硕(1999), 男, 硕士在读, 研究方向为模块化多电平换流器与柔性直流输电(E-mail: 1378441264@qq.com)

程婷(1982), 女, 学士, 馆员, 从事高压试验研究工作

通讯作者:
何柏娜(1977), 女, 博士, 副教授, 通信作者, 研究方向为电力系统暂态特性分析及高电压绝缘

中图分类号: TM76
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2024-03-22
- 修回日期: 2024-05-31
- 刊出日期: 2024-11-27

Adaptive current limiting control strategy for MMC-HVDC under bipolar fault conditions

1.
School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255000, China
2.
Wuhan NARI Limited Liability Company, State Grid Electric Power Research Institute, Wuhan 430077, China

摘要

摘要: 直流断路器(direct current circuit breaker, DCCB)广泛应用于柔直输电系统，其造价与开断电流密切相关。文中从减小断路器开断电流的角度出发，设计适用于半桥型模块化多电平换流器(modular multilevel converter, MMC)的自适应限流控制结构。在分析MMC直流侧短路电流特性的基础上，利用换流站输入阻抗幅值的变化反映其故障深度，定义换流站故障深度系数K_f；将K_f引入MMC控制结构，使其与桥臂电压参考值关联，提出针对MMC直流侧短路故障的自适应限流控制方法；在PSCAD/EMTDC平台搭建半桥型MMC柔直输电系统模型，模拟直流侧短路故障清除过程，验证限流控制的有效性。仿真结果表明：文中提出的限流控制方法可依据MMC不同故障深度，实现差异化限流控制，减小DCCB开断电流，提升故障清除速度。
- 柔直输电系统 /
- 直流断路器(DCCB) /
- 模块化多电平换流器(MMC) /
- 自适应限流 /
- 故障深度系数 /
- 差异化限流控制
Abstract: Direct current circuit breakers (DCCBs) are extensively utilized in flexible DC transmission systems, with their cost being intricately related to the breaking current. An adaptive current-limiting control structure tailored for half-bridge modular multilevel converters (MMCs) has been developed with the aim of reducing the breaking current of circuit breakers. By examining the short-circuit current characteristics on DC side of MMC, the variation in the input impedance amplitude of the converter station is utilized to indicate the extent of the fault. The coefficient K_f, which defines the fault depth of the converter station, is determined. K_f is incorporated into the control structure of MMC to align it with the reference value of the bridge arm voltage. A proposed method for adaptive current limiting control addresses DC side short circuit fault of MMCs. The model of the half-bridge MMC flexible DC transmission system is created using power systems computer-aided design/electromagnetic transients including DC (PSCAD/EMTDC) platform to model the clearance of DC side short-circuit faults and validate the effectiveness of current limiting control. The simulation results demonstrate that the proposed adaptive current limiting control technique can effectively implement differentiated current limiting control depending on the diverse fault depths of MMC. The breaking current of DCCB is reduced and the fault clearing speed is improved by this approach.

HTML全文

0. 引言

高压直流输电是解决可再生能源大规模输送的关键所在^[1-4]。基于模块化多电平换流器的高压直流输电(modular multilevel converter based high voltage direct current，MMC-HVDC)凭借其谐波畸变小、开关损耗低等特点，已成为高电压大容量直流输电的研究热点^[5-7]。架空线适宜远距离输电，但采用架空线会增加直流侧故障概率^[8]，其中双极短路是最严重的故障类型^[9-10]。半桥型MMC-HVDC系统阻尼小、惯量低，导致直流侧短路电流攀升速度快、峰值大，且无自然过零点，短路电流开断困难^[11-12]。因此抑制故障电流攀升，减小直流断路器(DC circuit breaker, DCCB)开断电流，对降低断路器投资成本具有重要意义^[13-14]。

半桥型MMC-HVDC的限流方法可分为实体限流与虚体限流。实体限流技术采用改进子模块结构、安装实体限流器等方式^[15-17]。文献[18]针对限流电感抑制故障电流衰减的问题，设计限流电感快速退出的限流器结构，在抑制短路电流的同时提升故障清除速度；文献[19]提出附加限流功能的DCCB结构，利用二极管实现储能电容、限流电感在故障回路内的投切，抑制故障电流。但上述限流设备须按照最严重故障进行配置，未考虑与故障严重程度匹配，可能导致过度抑制故障电流，缩短限流设备使用寿命。

虚体限流技术通过附加控制方式实现故障限流，包括改善桥臂电压控制与改进外环电压控制，相比于实体限流技术，虚体限流在成本节约与工程化应用方面具有优势^[20]。传统限流控制在故障后闭锁MMC会切断其交直两侧功率交换，不利于直流电网故障穿越运行^[21-22]。自适应限流控制可实现不同故障下的差异化限流，在抑制短路电流的同时保障功率传输，对于提高直流电网可靠性具有重要意义。文献[23]提出半桥型MMC-HVDC组合式限流控制策略，利用同时降低外环电压参考值与桥臂电压参考值的手段实现故障限流，兼具快速性与有效性，但控制方式相对繁琐。文献[24-25]将直流电流变化率乘以微分系数构造虚拟电感，降低桥臂电压参考值，实现故障限流，且正常运行时直流电流波动小。基于电流变化率的限流控制环节不会影响系统正常运行，但目前已有的文献缺乏对于故障深度评估及其表征方式的研究。

基于此，文中提出一种基于故障深度量化的自适应限流控制方法，定义换流站故障深度系数K_f，对故障深度进行表征及量化评估，在故障后利用K_f修正桥臂电压参考值，实现差异化故障限流控制，并在PSCAD/EMTDC仿真平台搭建柔直系统模型，验证所提限流控制的有效性。

1. 基于架空线的MMC双极短路故障分析

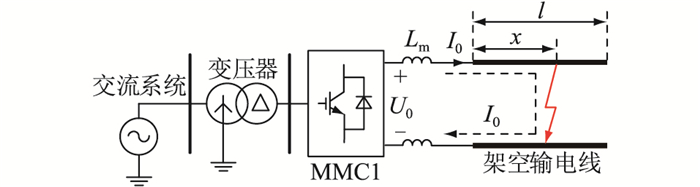
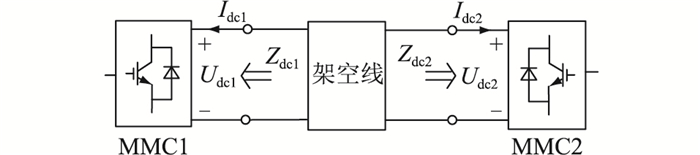
图 1为MMC-HVDC直流侧双极短路故障示意。图 1中, U₀为故障时换流站直流输出电压；I₀为故障时换流站直流输入电流；L_m为平波电抗器电感；l为架空线长度；x为故障位置到换流站直流出口距离。

图 1 MMC-HVDC双极短路故障示意

Figure 1. Schematic diagram of MMC-HVDC bipolar short circuit fault

下载: 全尺寸图片幻灯片

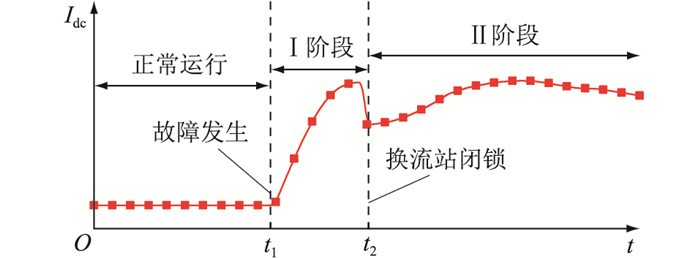
双极短路故障电流发展分为2个阶段，如图 2所示。Ⅰ阶段：故障发生至换流站闭锁；Ⅱ阶段：换流站闭锁以后。

图 2 双极短路故障电流发展过程

Figure 2. Bipolar short circuit fault current development process

下载: 全尺寸图片幻灯片

图 2可直观展示双极短路故障电流的发展过程。t₁时刻前，系统正常运行；t₁时刻，发生双极短路故障，换流站子模块电容放电，故障电流骤升，并发展至t₂时刻；t₂时刻，换流站闭锁，换流站子模块电容只充电不放电，故t₂时刻短路电流呈现断崖式下降；t₂时刻后，故障放电回路可等效为不控三相整流电路，短路电流逐步升至稳态值。

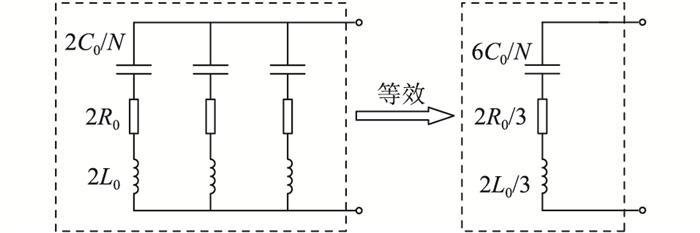
双极短路故障Ⅰ阶段的分析对于故障深度量化与故障清除研究尤为重要。Ⅰ阶段以子模块电容放电为主，忽略交流电网的分流作用，MMC内部可等效为图 3所示结构。图 3中，R₀为桥臂等效电阻；C₀为子模块电容；L₀为桥臂电感；N为桥臂子模块总数。

图 3 换流站闭锁前MMC等效电路

Figure 3. MMC equivalent circuit before converter station block

下载: 全尺寸图片幻灯片

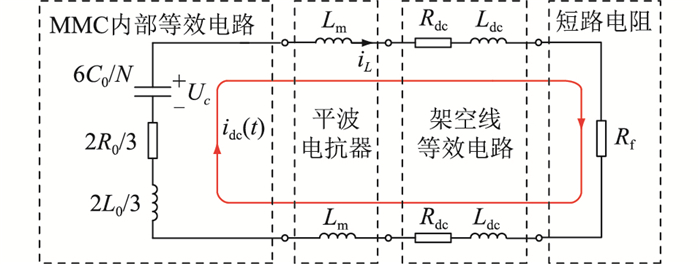
换流站与平波电抗器、直流侧架空线、短路电阻构成Ⅰ阶段的放电回路，其等效电路如图 4所示。图 4中，R_dc为架空线等效电阻，L_dc为架空线等效电感，设架空线单位长度电阻与单位长度电感分别为r₀与l₀，则R_dc=xr₀，L_dc=xl₀；R_f为短路电阻；U_c为换流站等效电容电压；i_L为电感电流；i_dc(t)为双极短路电流。

图 4 双极短路故障放电回路

Figure 4. Bipolar short circuit fault discharge circuit

下载: 全尺寸图片幻灯片

假设系统于t=0 s时发生短路故障，由换路定则可知，电容电压与电感电流不突变，换流站等效电容电压U_c可近似认为是故障时刻的直流输出电压U₀，同理电感电流i_L等于故障时刻的直流输出电流I₀。因此Ⅰ阶段放电过程初始条件为：

$\left\{\begin{array}{l} U_c\left(0_{+}\right)=U_c\left(0_{-}\right)=U_0 \\ i_L\left(0_{+}\right)=i_L\left(0_{-}\right)=I_0 \end{array}\right.$

(1)

式中：U_c(0_-)、U_c(0₊)分别为故障前、后换流站等效电容电压；i_L(0_-)、i_L(0₊)分别为故障前、后电感电流。

利用拉氏变换求解图 4电路，可得双极短路电流i_dc(t)的表达式为：

$i_{\mathrm{dc}}(t)=\frac{I_0}{\sin \left(\theta_1\right)} \mathrm{e}^{-t / \tau} \sin \left(\omega t-\theta_1\right)+\frac{U_0}{\omega L_{\text {eq }}} \mathrm{e}^{-t / \tau} \sin (\omega t)$

(2)

其中：

$\left\{\begin{array}{l} C_{\mathrm{eq}}=\frac{6 C_0}{N} \\ L_{\mathrm{eq}}=2\left(\frac{L_0}{3}+L_{\mathrm{m}}+x l_0\right) \\ R_{\mathrm{eq}}=2\left(\frac{L_0}{3}+x r_0\right)+R_{\mathrm{f}} \\ \tau=2 L_{\mathrm{eq}} / R_{\mathrm{eq}} \\ \theta_1=\arctan (\tau \omega) \\ \omega=\sqrt{\frac{1}{L_{\mathrm{eq}} C_{\mathrm{eq}}}-\frac{R_{\mathrm{eq}}^2}{4 L_{\mathrm{eq}}^2}} \end{array}\right.$

(3)

式中：L_eq为故障回路等效电感；R_eq为故障回路等效电阻；τ时间常数；C_eq为故障回路等效电容；ω为短路电流角频率；θ₁为短路电流相角。

实际工程中，R_eq²/(4L_eq²)≪1/(L_eqC_eq)^[26]，故θ₁≈π/2， $\omega \approx \sqrt{1 /\left(L_{\mathrm{eq}} C_{\mathrm{eq}}\right)}$ 。则式(2)经三角变换可进一步化简为：

$i_{\mathrm{dc}}(t)=\mathrm{e}^{-t / \tau} \sqrt{\frac{C_{\mathrm{eq}}}{L_{\mathrm{eq}}} U_0^2+I_0^2} \sin \left(\omega_2 t-\theta_2\right)$

(4)

其中：

$\left\{\begin{array}{l} \omega_2=\sqrt{\frac{1}{L_{\mathrm{eq}} C_{\mathrm{eq}}}} \\ \theta_2=\arctan \left(\frac{I_0}{U_0} \sqrt{\frac{L_{\mathrm{eq}}}{C_{\mathrm{eq}}}}\right) \end{array}\right.$

(5)

在实际工程中，考虑到继电保护装置动作的快速性，从故障发生到换流站闭锁的时间十分短暂，通常为数毫秒，故可以忽略式(4)中的指数衰减项，则式(4)可简化为：

$i_{\mathrm{dc}}(t)=\sqrt{\frac{C_{\mathrm{eq}}}{L_{\mathrm{eq}}} U_0^2+I_0^2} \sin \left(\omega_2 t-\theta_2\right)$

(6)

稳态运行状态下，U₀=Nu_c，u_c为子模块两端电压。由式(6)可得故障电流峰值为：

$i_{\text {max }}=\sqrt{\frac{3 C_0 N u_{\mathrm{c}}^2}{L_0 / 3+L_{\mathrm{m}}+x l_0}+I_0^2}$

(7)

由上述分析可知，短路故障电流Ⅰ阶段可以等效为RLC串联电路的零输入响应。当架空线故障位置远离换流站直流侧出口时，架空线等效阻抗增大，导致故障回路内等效电阻R_eq与等效电感L_eq增大，由式(6)可知，故障电流的峰值与角频率减小，放电过程发展缓慢，此时故障电流上升速度慢、峰值小。同理，当故障位置距换流站较近时，故障电流角频率高、峰值大，故障过程发展迅速。

2. 基于故障深度量化的限流控制原理

由前述分析可知，在双极短路故障Ⅰ阶段，换流站未闭锁，子模块投入故障回路，子模块电容向故障点持续放电。若通过附加控制减少投入故障回路的子模块数量，可削减子模块电容向故障点馈入的能量，实现故障限流。

MMC上、下桥臂参考电压u_pref、u_nref与共模电压参考值u_zref、差模电压参考值u_vref的关系可表示为：

$\left\{\begin{array}{l} u_{\mathrm{pref}}=-u_{\mathrm{vref}}+u_{\mathrm{zref}} \\ u_{\mathrm{nref}}=u_{\mathrm{vref}}+u_{\mathrm{zref}} \end{array}\right.$

(8)

对式(8)进行标幺化处理，等式两端同除以换流站直流侧端口电压U_dc，可得：

$\left\{\begin{array}{l} u_{\mathrm{p}}^*=\frac{1}{2}(1-m) \\ u_{\mathrm{n}}^*=\frac{1}{2}(1+m) \end{array}\right.$

(9)

式中：u_p^*、u_n^*分别为上、下桥臂电压参考标幺值；m为系统调制比，m=u_v/(0.5U_dc)，u_v为换流站交流端口电压。

系统正常运行时，上、下桥臂子模块投入的数量N_p与N_n可表示为：

$\left\{\begin{array}{l} N_{\mathrm{p}}=\operatorname{round}\left(u_{\mathrm{p}}^* N\right)=\operatorname{round}\left(\frac{1}{2}(1-m) N\right) \\ N_{\mathrm{n}}=\operatorname{round}\left(u_{\mathrm{n}}^* N\right)=\operatorname{round}\left(\frac{1}{2}(1+m) N\right) \end{array}\right.$

(10)

式中：round(·)为取整函数。

2.1 换流站故障深度量化方法

从直流侧看向换流站内部，换流站输入阻抗定义示意如图 5所示。图 5中，U_dcj为换流站MMCj的直流侧端口电压，j=1, 2；I_dcj为换流站MMCj的直流侧端口输入电流；Z_dcj为换流站MMCj的输入阻抗。

图 5 换流站输入阻抗

Figure 5. Converter station input impedance

下载: 全尺寸图片幻灯片

换流站输入阻抗绝对值|Z_dc|可表示为：

$\left|Z_{\mathrm{dc}}\right|=\left|\frac{U_{\mathrm{dc}}}{I_{\mathrm{dc}}}\right|$

(11)

式中：I_dc为换流站直流侧端口输入电流。

$\begin{gathered} K_{\mathrm{f}}=1-\left|Z_{\mathrm{dc}}^*\right|=1-\frac{\left|Z_{\mathrm{dc}}\right|}{\left|Z_{\mathrm{dcb}}\right|}=1-\frac{\left|U_{\mathrm{dc}} / I_{\mathrm{dc}}\right|}{\left|U_{\mathrm{deN}} / I_{\mathrm{deN}}\right|} \\ K_{\mathrm{f}} \in[0, 1] \end{gathered}$

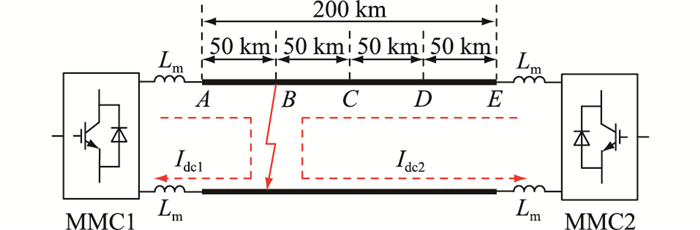
(12)

图 6为MMC-HVDC仿真模型，设置A、B、C、D、E共5个故障点。基于图 6，针对不同故障位置对两端换流站故障深度系数K_f的影响进行仿真分析。

图 6 MMC-HVDC系统拓扑

Figure 6. MMC-HVDC system topology

下载: 全尺寸图片幻灯片

图 6中，MMC1作逆变站运行，采用定有功功率控制和定无功功率控制，有功功率整定值为400 MW，无功功率整定值为0 Mvar；MMC2作整流站运行，采用定直流电压控制和定无功功率控制，直流电压整定值为400 kV，无功功率整定值为0 Mvar。两换流站以架空线联接，全长200 km，模型参数见表 1。

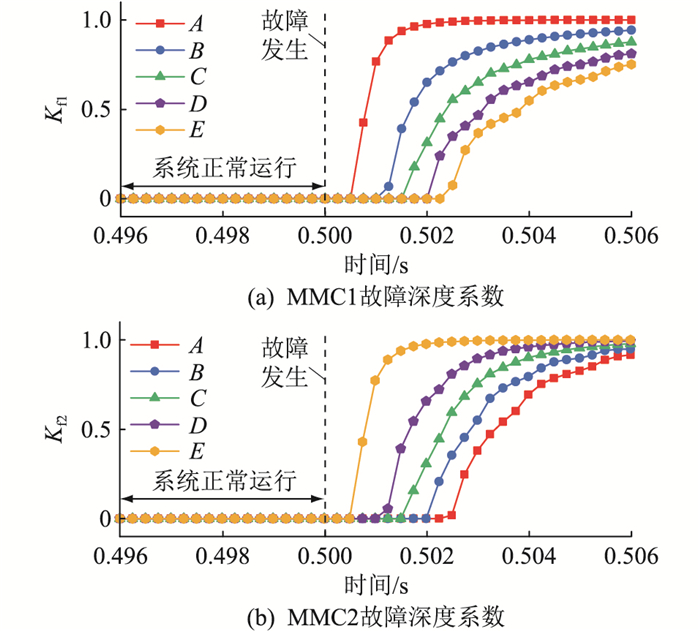
表 1 MMC-HVDC系统参数

Table 1. MMC-HVDC system parameters

参数	数值
直流电压/kV	±400
交流电压/kV	220
系统容量/(MV·A)	800
单个桥臂子模块数量	200
子模块电容/mF	6
子模块导通电阻/Ω	0.01
桥臂电抗器电感/mH	76
平波电抗器电感/mH	76

下载: 导出CSV

| 显示表格

假设系统在t=0.5 s时发生双极短路故障，在t=0.506 s时换流站闭锁，不同故障位置下两端换流站故障深度系数变化趋势如图 7所示。图中K_f1、K_f2分别为MMC1、MMC2故障深度系数。

图 7 换流站故障深度系数变化趋势

Figure 7. Variation trend of fault depth coefficients of converter stations

下载: 全尺寸图片幻灯片

由图 7可知，系统正常运行时，两端换流站故障深度系数K_f为0，故障发生后，K_f逐渐增大，K_f与换流站故障深度呈正相关，故障愈严重，K_f数值愈大。仿真结果表明：架空线同一故障位置对两端换流站K_f影响各异。故障近端换流站由于其故障回路等效阻抗小，短路电流变化迅速，K_f曲线陡度大，故障程度相对严重；故障远端换流站与之相反，K_f曲线陡度小，故障程度较轻。

故障发生后，故障近端换流站K_f大于远端换流站K_f。如图 7所示，架空线E点故障后，近端换流站MMC2故障深度系数K_f2大于远端换流站MMC1故障深度系数K_f1。仿真结果表明，通过比较K_f大小可区分不同换流站的故障程度。

各位置故障时，两端换流站闭锁时刻的K_f峰值如表 2所示。

表 2 闭锁时故障深度系数峰值

Table 2. Peak value of fault depth coefficient during lockout

故障位置	K_f1峰值	K_f2峰值
A	1	0.915
B	0.943	0.948
C	0.875	0.933
D	0.810	0.990
E	0.752	1

下载: 导出CSV

| 显示表格

2.2 基于故障深度量化的自适应限流控制设计

基于故障深度系数K_f，对式(10)修正，修正后的桥臂投入子模块数量为：

$\left\{\begin{array}{l} N_{\mathrm{p}}=\operatorname{round}\left(\frac{1}{2}(1-m)\left(1-K_{\mathrm{f}}\right) N\right) \\ N_{\mathrm{n}}=\operatorname{round}\left(\frac{1}{2}(1+m)\left(1-K_{\mathrm{f}}\right) N\right) \end{array}\right.$

(13)

由式(13)可知，K_f与子模块投入数量呈负相关。当换流站故障严重时，K_f较大，子模块投入数量较少；反之，故障深度较浅时，子模块投入数量较多。

基于式(13)，改进MMC控制系统，实时监测直流电压U_dc与直流电流变化率dI_dc/dt，并分别设定直流电压跌落阈值U_th与电流变化率阈值v_th，系统正常运行时，U_dc与dI_dc/dt满足式(14)。

$\left\{\begin{array}{l} U_{\mathrm{dc}} \geqslant U_{\mathrm{th}} \\ \mathrm{~d} I_{\mathrm{dc}} / \mathrm{d} t \leqslant v_{\mathrm{th}} \end{array}\right.$

(14)

利用比较器对监测量与设定阈值实时比较，监测量超过设定阈值时输出为1，反之输出为0。当直流电压U_dc < U_th且直流电流变化率dI_dc/dt>v_th时，输出故障检测结果为1，限流控制装置启动，桥臂电压参考值缩小为原来的1-K_f倍。基于故障深度系数K_f的限流控制结构设计如图 8所示。

图 8 基于故障深度量化的限流控制结构

Figure 8. Current limiting control structure based on fault depth quantification

下载: 全尺寸图片幻灯片

图 8所示控制结构在MMC原有控制系统中添加故障深度量化模块与故障检测模块。故障检测模块基于式(14)双监测量判据输出故障检测结果，两判据在逻辑上取与的关系，防止系统调整运行状态时，单一监测量变化引起故障误判；故障深度量化模块输出换流站故障深度系数，反映换流站故障严重程度，同时调整桥臂电压参考值，抑制故障电流。

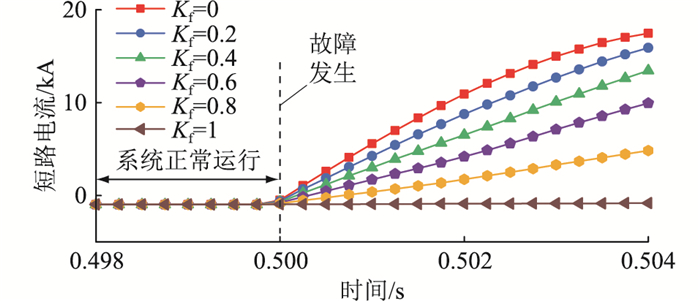
基于图 8，假设t=0.5 s时换流站直流侧发生双极短路故障，不同故障深度对短路电流上升阶段的影响如图 9所示。

图 9 不同故障深度下短路电流的抑制效果

Figure 9. The suppression effect of short circuit current under different values of fault depth

下载: 全尺寸图片幻灯片

由图 9可得，短路电流抑制效果与换流站故障深度成正比，故障深度系数K_f越大，限流控制对故障电流的抑制效果越显著，短路电流的陡度愈小。当K_f=1时，故障程度最严重，在限流作用下，故障电流无明显上升趋势。由式(13)可知，子模块投入数量与K_f呈负相关，换流站故障程度愈严重，子模块投入数量愈少，故障电流抑制效果愈明显。因此，该控制方式可依据不同故障深度调整子模块投入数量，以抑制故障电流。

2.3 计及K_f的MMC直流侧短路电流分析

限流控制启动后，桥臂子模块的投切改变了故障回路参数，此时的MMC等效电容C′_eq可表示为：

$C_{\mathrm{eq}}^{\prime}=\frac{6 C_0}{\left(1-K_{\mathrm{f}}\right) N}$

(15)

限流控制后的直流侧输出电压U′₀可表示为：

$U_0^{\prime}=\left(1-K_{\mathrm{f}}\right) N u_{\mathrm{c}}$

(16)

将式(15)、式(16)代入式(5)，可得限流控制启动后的故障电流Ⅰ阶段角频率ω′与相位θ′为：

$\left\{\begin{array}{l} \omega^{\prime}=\sqrt{\frac{\left(1-K_{\mathrm{f}}\right) N}{6 C_0 L_{\mathrm{eq}}}} \\ \theta^{\prime}=\arctan \left(I_0 \sqrt{\frac{L_{\mathrm{eq}}}{6 C_0 N u_{\mathrm{c}}\left(1-K_{\mathrm{f}}\right)}}\right) \end{array}\right.$

(17)

将式(15)、式(16)代入式(7)，可得限流控制下的系统Ⅰ阶段故障电流峰值i′_max为：

$i_{\text {max }}^{\prime}=\sqrt{\frac{3 C_0\left(1-K_{\mathrm{f}}\right) N u_{\mathrm{c}}^2}{L_0 / 3+L_{\mathrm{m}}+x l_0}+I_0^2}$

(18)

综合式(17)、式(18)，可得计及K_f的MMC直流侧短路电流Ⅰ阶段表达式为：

$i_{\mathrm{dc}}^{\prime}(t)=i_{\max }^{\prime} \sin \left(\omega^{\prime} t-\theta^{\prime}\right)$

(19)

分析式(17)、式(18)可得，短路电流Ⅰ阶段角频率ω′、峰值i′_max与换流站故障深度系数K_f呈负相关，K_f增大则故障电流角频率与峰值减小。因此，随着短路故障的发展，换流站K_f增大，故障电流角频率ω′降低，峰值i′_max减小，短路电流被抑制。

由2.2节分析可知，故障近端换流站K_f增速快，峰值大，此时限流控制下的故障电流角频率ω′与峰值i′_max快速减小，短路电流上升趋势被迅速抑制；而故障远端换流站情况与之相反，受远端换流站K_f增速慢、峰值小的特性影响，短路电流抑制效果相对较弱。综上可得，该限流控制方式在理论上可实现针对不同故障深度的差异化限流控制。

3. 架空线双极短路仿真分析

基于图 6所示MMC-HVDC拓扑，在不同位置设置永久性双极短路故障，t=0.3 s时发生双极短路故障，仿真结果如图 10所示。

图 10 双极短路故障仿真结果

Figure 10. Simulation results of bipolar short circuit fault

下载: 全尺寸图片幻灯片

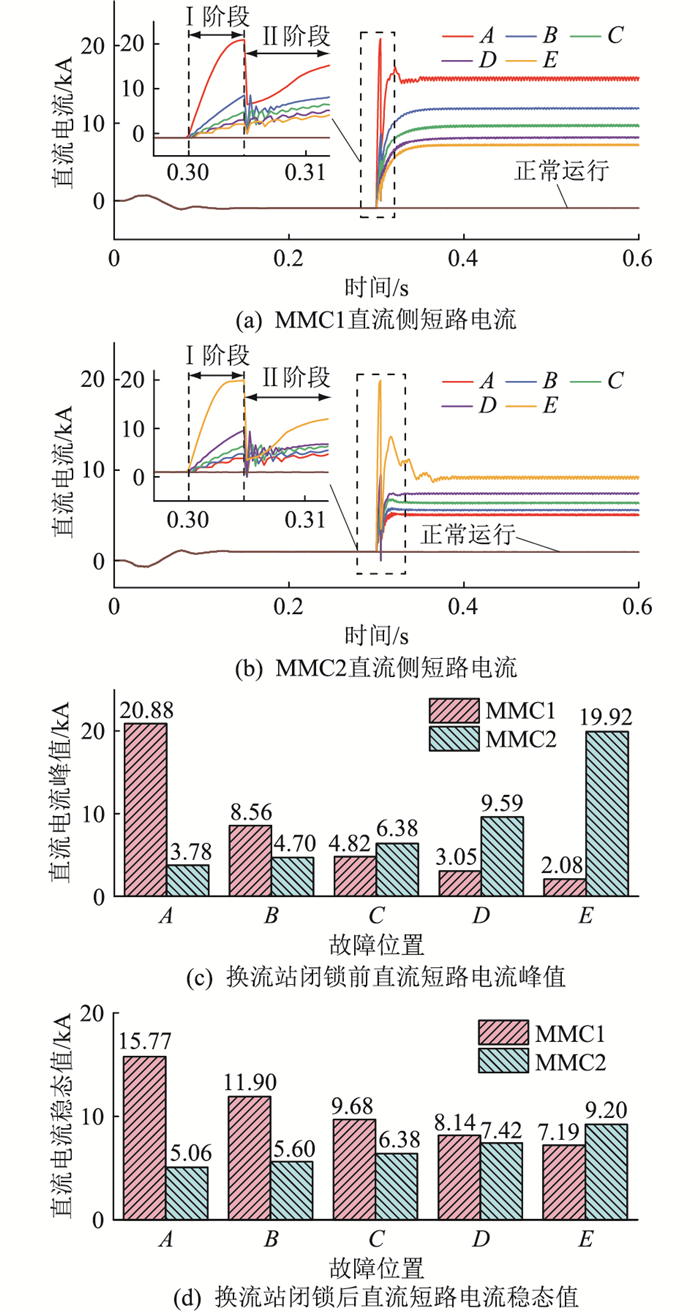
如图 10(a)、(b)所示，t=0.3 s时系统发生双极短路故障，短路电流迅速攀升，t=0.306 s时换流站闭锁，短路电流先下降后随故障发展逐步上升至稳态值。当故障点位于换流站直流出口时，短路电流攀升速度最快、峰值最大。以MMC1侧为例，A点位于MMC1直流侧出口，此时故障电流攀升速度最快，上升阶段陡度最大；E点远离MMC1，其故障电流攀升速度最慢，上升陡度最小。短路电流上升阶段陡度随故障点远离换流站而减小，由于故障回路等效感抗的抑制作用，故障远端换流站回路等效感抗大于故障近端，因此，故障远端换流站短路电流上升陡度低于故障近端。

由图 10(c)、(d)可知，A点故障时，MMC1侧短路电流闭锁前峰值与闭锁后稳态值最大，分别为20.88 kA与15.77 kA；E点故障时MMC1侧短路电流最小，分别为2.08 kA与7.19 kA。短路电流闭锁前峰值与闭锁后稳态值均随故障点远离换流站而减小，故障回路等效感抗是换流站闭锁前短路电流峰值的主要影响因素，故障远端换流站由于其放电回路感抗大，短路电流峰值小于近端换流站；换流站闭锁后短路电流稳态值主要受故障回路等效电阻影响，远端换流站放电回路等效阻值较大，因此其短路电流稳态值小于近端换流站。

4. 自适应限流控制仿真分析

为验证所提自适应限流方案的有效性，文中分别在双端柔直输电系统与四端柔性直流电网的仿真模型中，针对架空线不同位置的双极短路故障，模拟故障清除过程。

4.1 故障清除阶段划分

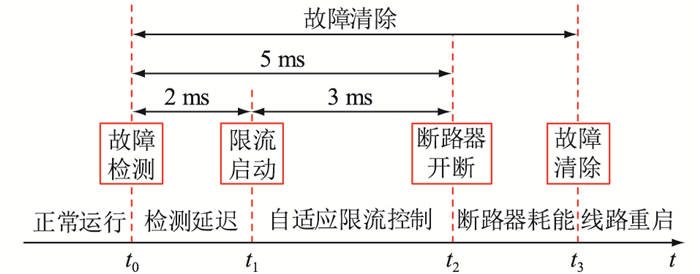
直流侧故障清除过程如图 11所示。

图 11 故障清除过程示意

Figure 11. Schematic diagram of fault clearing process

下载: 全尺寸图片幻灯片

t₀时刻短路故障发生，故障电流迅速上升；经保护延时，t₁时刻自适应限流控制启动，桥臂电压参考值减小，限制故障电流；t₂时刻直流断路器开断，故障电流逐渐减小至零；t₃时刻故障清除。

4.2 双端柔直系统故障清除仿真

基于图 5所示双端MMC-HVDC模型，假设系统在t=0.5 s时发生双极短路故障，短路电阻R_f=0.01 Ω，考虑直流电网线路保护装置的延时为2 ms^[27]、DCCB开断时间为3 ms^[28]，t=0.502 s时启动自适应限流控制模块，持续作用至t=0.505 s时断路器开断。以换流站最严峻故障和最轻微故障为例，故障清除过程如图 12、图 13所示。

图 12 MMC1故障清除过程

Figure 12. MMC1 fault clearing process

下载: 全尺寸图片幻灯片

图 13 MMC2故障清除过程

Figure 13. MMC2 fault clearing process

下载: 全尺寸图片幻灯片

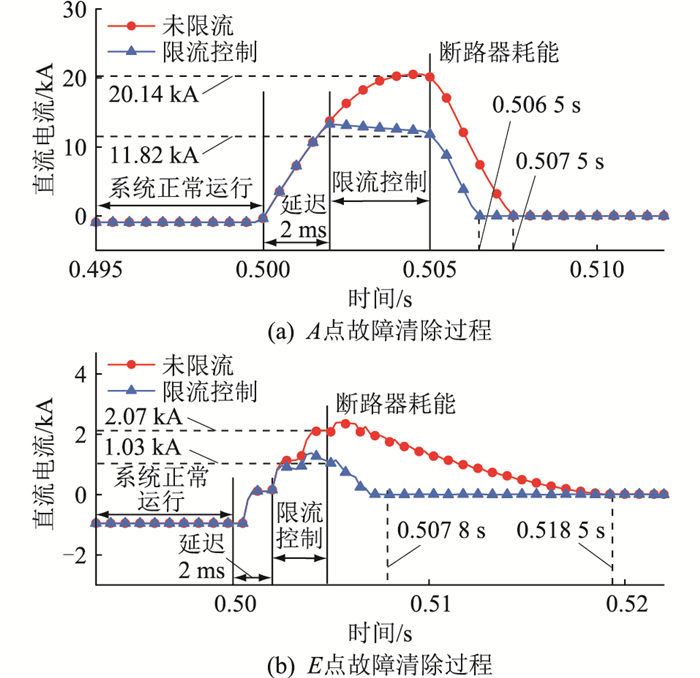
如图 12所示，短路电流总体呈先上升后下降趋势。无限流控制情况下，故障电流在DCCB开断前快速上升；采用限流控制2 ms后，自适应限流控制使短路电流上升陡度减小。仿真结果表明，自适应限流控制显著降低了DCCB开断电流。MMC1最严重故障情况下，DCCB开断电流由20.14 kA减小至11.82 kA，利于故障电流开断，降低了系统对于DCCB的性能需求，其余故障位置对应的开断电流在限流控制前后的对比如表 3所示。

表 3 不同故障位置下MMC1侧断路器开断电流对比

Table 3. Comparison of the breaking current of MMC1 circuit breaker at different fault locations kA

故障位置	开断电流		变化量
故障位置	无限流	有限流	变化量
A	20.14	11.82	8.32
B	8.68	3.43	5.25
C	4.80	1.93	2.87
D	3.09	1.35	2.46
E	2.07	1.03	1.04

下载: 导出CSV

| 显示表格

分析表 3可得，开断电流在限流控制前后的变化量与故障位置相关。其中，A点距MMC1直流出口最近，MMC1故障最严峻，开断电流变化量最大；而E点距MMC1直流出口最远，MMC1故障轻微，开断电流仅减小1.04 kA。仿真结果表明，自适应限流控制可依据换流站故障深度，调整故障回路子模块投入数量，抑制故障电流。

由图 12可知，受故障回路等效感抗影响，故障清除时间随故障点远离换流站而延长。E点故障清除用时18.5 ms，远大于A点。MMC1侧故障清除用时在限流控制前后对比如表 4所示。

表 4 不同故障位置下MMC1侧故障清除时间对比

Table 4. Comparison of the time when a fault is cleared on MMC1 at different fault locations

故障位置	清除时间/ms		缩短时间/ms	缩短比例/%
故障位置	无限流	有限流	缩短时间/ms	缩短比例/%
A	7.5	6.5	1.0	13.3
B	14.5	6.8	7.7	53.1
C	15.3	7.0	8.3	54.2
D	17.0	7.3	9.7	57.0
E	18.5	7.8	10.7	57.8

下载: 导出CSV

| 显示表格

分析图 12与表 4可得，限流控制提升了断路器耗能阶段故障电流衰减速度，短路电流清除时间较未限流时明显缩短。其中，受故障回路参数影响，当MMC1侧DCCB开断，E点故障清除速度提升效果最显著，清除时间缩短57.8%。仿真结果表明，自适应限流控制可削减换流站向故障点的能量馈入，降低DCCB开断电流，缩短故障清除用时。

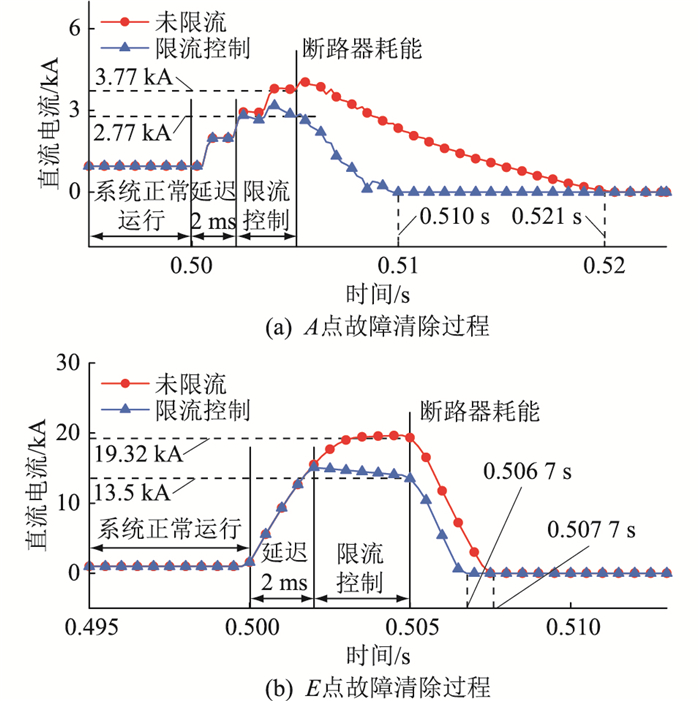
由图 13可知，MMC2侧DCCB开断，在限流控制下，E点的开断电流由19.32 kA降低至13.5 kA，限流率30.1%，其余故障位置开断电流的限流前后对比如表 5所示。

表 5 不同故障位置下MMC2侧断路器开断电流对比

Table 5. Comparison of the breaking current of MMC2 circuit breaker at different fault locations kA

故障位置	开断电流		变化量
故障位置	无限流	有限流	变化量
A	3.77	2.77	1.00
B	4.72	3.05	1.67
C	6.27	3.62	2.65
D	9.55	5.08	4.47
E	19.32	13.50	5.82

下载: 导出CSV

| 显示表格

由表 5可知，受故障点到换流站距离影响，MMC2侧各故障点开断电流变化量与MMC1侧相反。故障点位于MMC2直流出口处，开断电流最大，经限流后减小了5.82 kA，结果表明，该限流控制可减小DCCB开断电流，降低其投资成本。

MMC2侧故障清除时间在限流控制前后的对比如表 6所示。其中，受架空线感抗影响，A点故障时清除时间持续最久。

表 6 不同故障位置下MMC2侧故障清除时间对比

Table 6. Comparison of the time when a fault is cleared on MMC2 at different fault locations

故障位置	清除时间/ms		缩短时间/ms	缩短比例/%
故障位置	无限流	有限流	缩短时间/ms	缩短比例/%
A	21.0	10.0	11.0	52.4
B	19.0	8.5	10.5	55.3
C	18.0	8.0	10.0	55.5
D	11.8	7.3	4.5	38.1
E	7.8	6.8	1.0	13.0

下载: 导出CSV

| 显示表格

分析图 13与表 6可得，减小DCCB开断电流可有效提高断路器耗能阶段故障电流衰减速度，衰减速度亦受线路参数影响，故障点距MMC2直流出口较远时，其故障回路等效感抗占比大，故障电流衰减速度提升显著。

4.3 四端柔直电网故障清除仿真

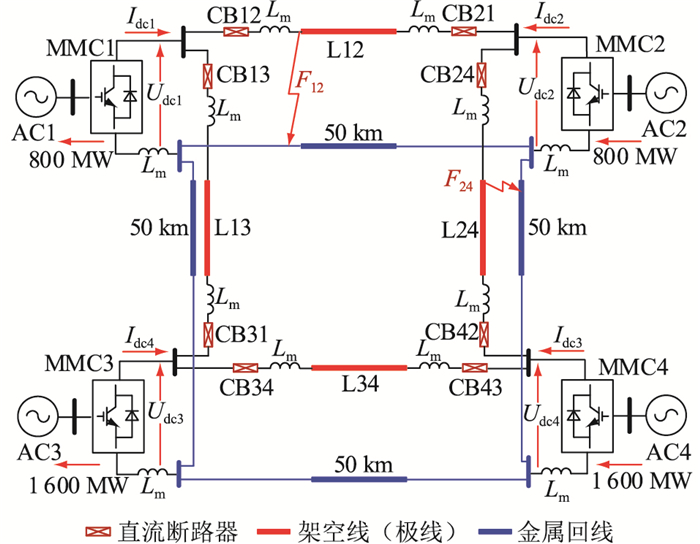
基于图 14所示四端柔性直流电网，模拟电网直流侧双极短路故障清除过程。

图 14 四端柔性直流电网

Figure 14. Four-terminal flexible DC power grid

下载: 全尺寸图片幻灯片

图 14中4个换流站均采用半桥型MMC拓扑，其具体参数见表 7。

表 7 四端柔性直流电网参数

Table 7. Four-terminal flexible DC power grid parameters

参数	MMC1	MMC2	MMC3	MMC4
额定容量/MW	800	800	1 600	1 600
额定直流电压/kV	800	800	800	800
交流电压/kV	220	220	220	220
桥臂电感/mH	44	44	88	88
子模块电容/mF	6	6	10	10
子模块数	200	200	200	200

下载: 导出CSV

| 显示表格

MMC2控制系统直流电压，其余换流站均为功率站。各换流站之间以50 km架空线联接，直流电网稳态运行时，MMC2、MMC4输出功率分别为800、1 600 MW，MMC1、MMC3吸收功率分别为800、1 600 MW。DCCB均采用混合式直流断路器拓扑，限流电抗器电感L_m为200 mH。

在图 14中F₁₂、F₂₄处分别设置永久性双极短路故障，仿真结果如图 15所示。假设t=0.5 s时，架空线发生双极短路故障，短路电阻R_f=0.01 Ω。各换流站采用如图 8所示控制结构，故障发生后，经系统保护延迟2 ms后，自适应限流控制投入，持续作用至t=0.505 s断路器动作。

图 15 四端柔直电网故障清除过程

Figure 15. Fault clearing process for four-terminal flexible DC power grid

下载: 全尺寸图片幻灯片

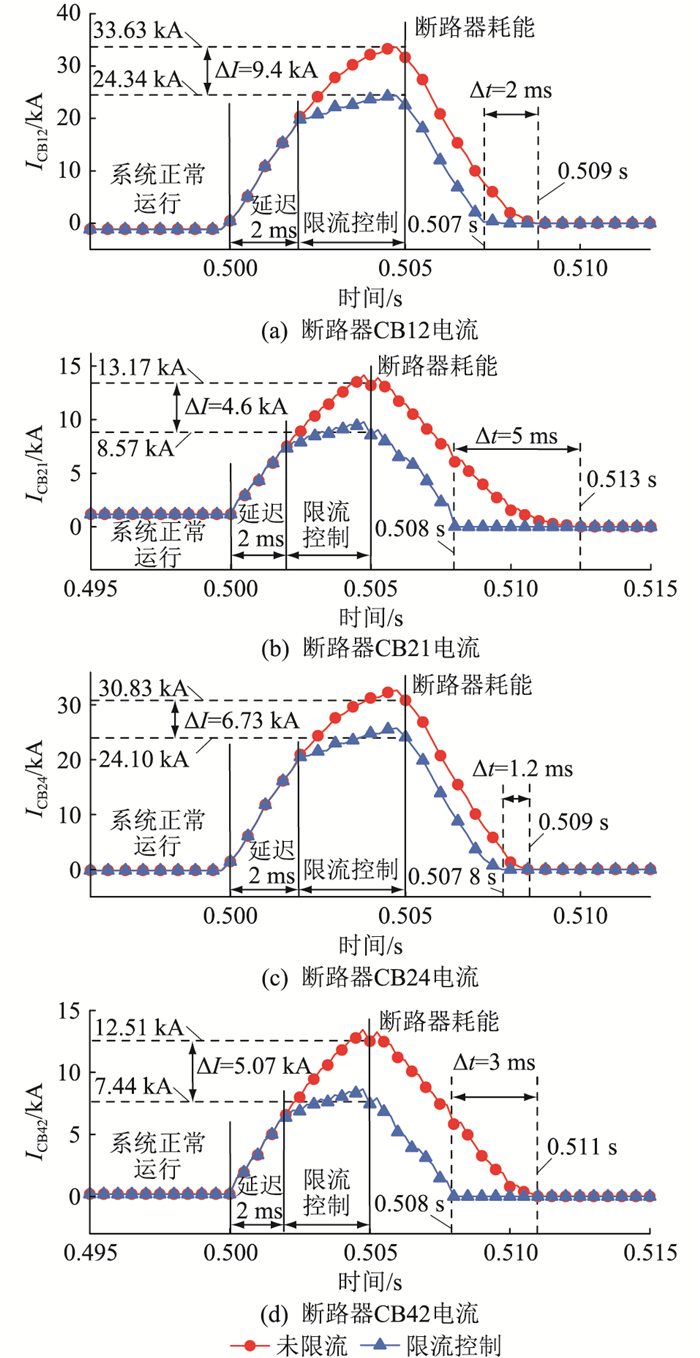
分析图 15可知，架空线发生双极短路故障后，无限流控制下，短路电流在DCCB开断前快速上升；限流控制启动后，在t=0.502 s后，受K_f对桥臂电压参考值修正的影响，故障电流上升阶段陡度被抑制。

与双端系统限流控制效果类似，该限流控制可有效降低四端电网中故障线路两侧DCCB的开断电流。其中，故障点近端DCCB开断电流变化量ΔI大于其远端DCCB。如图 15(a)、(b)所示，F₁₂处故障后，故障相对严重的MMC1侧断路器CB12开断电流在限流后的变化量ΔI为9.4 kA，而MMC2侧的CB21开断电流变化量ΔI仅4.6 kA。仿真结果表明，文中提出的限流控制方式可实现针对不同故障深度情况下的差异化限流控制。

该限流控制方式有效缩短了短路线路的故障清除用时，提升了故障清除速度。故障清除速度提升效果受故障位置影响，当某点故障时，其远端DCCB故障清除速度提升效果优于近端DCCB。在图 15(c)、(d)中，F₄₂处故障时，CB24完成开断用时由9 ms减少至7.8 ms，时间变化量Δt为1.2 ms，故障清除用时仅缩短13.3%；而CB42故障清除用时减少3 ms，较未限流时缩短27.3%。

综上所述，基于故障深度量化的自适应限流控制可有效提升短路电流清除速度，缩短故障清除时间。针对同一故障点而言，其远端换流站侧DCCB故障清除速度提升效果显著，而近端换流站侧提升效果相对较弱。

该限流控制方式可以实现针对换流站不同故障深度下的差异化限流控制，有效减小断路器开断电流，降低断路器投资成本。对同一换流站而言，其直流出口处故障时的DCCB开断电流在限流前后的变化量ΔI最大，且ΔI随故障点远离换流站而减小。

5. 结论

文中提出一种针对MMC直流侧短路故障的自适应限流控制方法，基于故障后换流站直流侧输入阻抗的变化，定义换流站故障深度系数K_f，将K_f与换流站桥臂电压参考值相关联，实现了直流侧故障限流，并得出以下结论：

(1) 文中提出的换流站故障深度系数K_f可对换流站故障严重程度进行量化表征，K_f数值愈大，换流站故障愈严重，通过比较K_f大小，可有效区分不同换流站故障深度，为后续针对不同故障深度下的差异化限流控制提供量化依据。

(2) 文中设计的自适应限流控制结构，可以依据换流站故障深度变化情况，实现不同故障的差异化限流。仿真结果表明，该自适应限流控制结构能够有效减小断路器开断电流，提升断路器耗能阶段故障电流衰减速度，缩短故障清除时间，降低断路器投资成本。

致谢: 本文得到山东省研究生教育质量提升计划(SDYAL2022114)资助，谨此致谢！

图 1 MMC-HVDC双极短路故障示意

Figure 1. Schematic diagram of MMC-HVDC bipolar short circuit fault

下载: 全尺寸图片幻灯片

图 2 双极短路故障电流发展过程

Figure 2. Bipolar short circuit fault current development process

下载: 全尺寸图片幻灯片

图 3 换流站闭锁前MMC等效电路

Figure 3. MMC equivalent circuit before converter station block

下载: 全尺寸图片幻灯片

图 4 双极短路故障放电回路

Figure 4. Bipolar short circuit fault discharge circuit

下载: 全尺寸图片幻灯片

图 5 换流站输入阻抗

Figure 5. Converter station input impedance

下载: 全尺寸图片幻灯片

图 6 MMC-HVDC系统拓扑

Figure 6. MMC-HVDC system topology

下载: 全尺寸图片幻灯片

图 7 换流站故障深度系数变化趋势

Figure 7. Variation trend of fault depth coefficients of converter stations

下载: 全尺寸图片幻灯片

图 8 基于故障深度量化的限流控制结构

Figure 8. Current limiting control structure based on fault depth quantification

下载: 全尺寸图片幻灯片

图 9 不同故障深度下短路电流的抑制效果

Figure 9. The suppression effect of short circuit current under different values of fault depth

下载: 全尺寸图片幻灯片

图 10 双极短路故障仿真结果

Figure 10. Simulation results of bipolar short circuit fault

下载: 全尺寸图片幻灯片

图 11 故障清除过程示意

Figure 11. Schematic diagram of fault clearing process

下载: 全尺寸图片幻灯片

图 12 MMC1故障清除过程

Figure 12. MMC1 fault clearing process

下载: 全尺寸图片幻灯片

图 13 MMC2故障清除过程

Figure 13. MMC2 fault clearing process

下载: 全尺寸图片幻灯片

图 14 四端柔性直流电网

Figure 14. Four-terminal flexible DC power grid

下载: 全尺寸图片幻灯片

图 15 四端柔直电网故障清除过程

Figure 15. Fault clearing process for four-terminal flexible DC power grid

下载: 全尺寸图片幻灯片

表 1 MMC-HVDC系统参数

Table 1 MMC-HVDC system parameters

参数	数值
直流电压/kV	±400
交流电压/kV	220
系统容量/(MV·A)	800
单个桥臂子模块数量	200
子模块电容/mF	6
子模块导通电阻/Ω	0.01
桥臂电抗器电感/mH	76
平波电抗器电感/mH	76

下载: 导出CSV

表 2 闭锁时故障深度系数峰值

Table 2 Peak value of fault depth coefficient during lockout

故障位置	K_f1峰值	K_f2峰值
A	1	0.915
B	0.943	0.948
C	0.875	0.933
D	0.810	0.990
E	0.752	1

下载: 导出CSV

表 3 不同故障位置下MMC1侧断路器开断电流对比

Table 3 Comparison of the breaking current of MMC1 circuit breaker at different fault locations kA

故障位置	开断电流		变化量
故障位置	无限流	有限流	变化量
A	20.14	11.82	8.32
B	8.68	3.43	5.25
C	4.80	1.93	2.87
D	3.09	1.35	2.46
E	2.07	1.03	1.04

下载: 导出CSV

表 4 不同故障位置下MMC1侧故障清除时间对比

Table 4 Comparison of the time when a fault is cleared on MMC1 at different fault locations

故障位置	清除时间/ms		缩短时间/ms	缩短比例/%
故障位置	无限流	有限流	缩短时间/ms	缩短比例/%
A	7.5	6.5	1.0	13.3
B	14.5	6.8	7.7	53.1
C	15.3	7.0	8.3	54.2
D	17.0	7.3	9.7	57.0
E	18.5	7.8	10.7	57.8

下载: 导出CSV

表 5 不同故障位置下MMC2侧断路器开断电流对比

Table 5 Comparison of the breaking current of MMC2 circuit breaker at different fault locations kA

故障位置	开断电流		变化量
故障位置	无限流	有限流	变化量
A	3.77	2.77	1.00
B	4.72	3.05	1.67
C	6.27	3.62	2.65
D	9.55	5.08	4.47
E	19.32	13.50	5.82

下载: 导出CSV

表 6 不同故障位置下MMC2侧故障清除时间对比

Table 6 Comparison of the time when a fault is cleared on MMC2 at different fault locations

故障位置	清除时间/ms		缩短时间/ms	缩短比例/%
故障位置	无限流	有限流	缩短时间/ms	缩短比例/%
A	21.0	10.0	11.0	52.4
B	19.0	8.5	10.5	55.3
C	18.0	8.0	10.0	55.5
D	11.8	7.3	4.5	38.1
E	7.8	6.8	1.0	13.0

下载: 导出CSV

表 7 四端柔性直流电网参数

Table 7 Four-terminal flexible DC power grid parameters

参数	MMC1	MMC2	MMC3	MMC4
额定容量/MW	800	800	1 600	1 600
额定直流电压/kV	800	800	800	800
交流电压/kV	220	220	220	220
桥臂电感/mH	44	44	88	88
子模块电容/mF	6	6	10	10
子模块数	200	200	200	200

下载: 导出CSV

参考文献(28)

[1]	刘洪波, 阎禹同, 王曦, 等. 多馈入交直流混联系统小干扰稳定研究综述[J]. 发电技术, 2023, 44(4): 565-575. LIU Hongbo, YAN Yutong, WANG Xi, et al. A review of small signal stability studies of multi-infeed AC-DC hybrid system[J]. Power Generation Technology, 2023, 44(4): 565-575.
[2]	谢小荣, 贺静波, 毛航银, 等. "双高"电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-474. XIE Xiaorong, HE Jingbo, MAO Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-474.
[3]	管恩齐, 何晋, 骆通. 含直流潮流控制器的真双极多端柔性直流电网潮流计算研究[J]. 电力电容器与无功补偿, 2023, 44(2): 68-76. GUAN Enqi, HE Jin, LUO Tong. Research on power flow calculation of true bipolar multi-terminal flexible DC power grid with DC power flow controller[J]. Power Capacitor & Reactive Power Compensation, 2023, 44(2): 68-76.
[4]	汪惟源, 窦飞, 蔡晖, 等. 柔性输电技术在江苏跨江输电通道的应用研究[J]. 电力电容器与无功补偿, 2022, 43(2): 141-146. WANG Weiyuan, DOU Fei, CAI Hui, et al. Research on application of flexible AC/DC transmission technologies in yangtze-river-crossing transmission channels of Jiangsu Province[J]. Power Capacitor & Reactive Power Compensation, 2022, 43(2): 141-146.
[5]	华文, 董炜, 叶琳, 等. PLL-GFC型MMC-HVDC暂态同步稳定性研究[J]. 浙江电力, 2023, 42(1): 13-22. HUA Wen, DONG Wei, YE Lin, et al. A study of the transient synchronization stability of PLL-GFC-based MMC-HVDC systems[J]. Zhejiang Electric Power, 2023, 42(1): 13-22.
[6]	贺之渊, 陆晶晶, 刘天琪, 等. 柔性直流电网故障电流抑制关键技术与展望[J]. 电力系统自动化, 2021, 45(2): 173-183. HE Zhiyuan, LU Jingjing, LIU Tianqi, et al. Key technologies and prospect of fault current suppression in flexible DC power grid[J]. Automation of Electric Power Systems, 2021, 45(2): 173-183.
[7]	聂铭, 和敬涵, 李猛, 等. 基于半桥MMC特征信号注入的柔性直流线路频变参数辨识[J]. 电力系统保护与控制, 2023, 51(24): 33-43. NIE Ming, HE Jinghan, LI Meng, et al. Flexible DC line frequency-dependent parameter identification based on characteristic signal injection with HB-MMC[J]. Power System Protection and Control, 2023, 51(24): 33-43.
[8]	ZHANG J R, HE B N, HE X M, et al. Research on fault clearing scheme for half-bridge modular multilevel converters high voltage DC based on overhead transmission lines[J]. International Journal of Emerging Electric Power Systems, 2021, 22(1): 61-72.
[9]	王泽青, 夏成军, 赖胜杰, 等. 混合型MMC非闭锁型直流故障穿越的故障等效模型[J]. 电力工程技术, 2023, 42(2): 103-111. https://www.epet-info.com/dlgcjs/article/abstract/220509655?st=search WANG Zeqing, XIA Chengjun, LAI Shengjie, et al. Fault equivalent model for non-blocking DC fault ride-through of hybrid MMC[J]. Electric Power Engineering Technology, 2023, 42(2): 103-111. https://www.epet-info.com/dlgcjs/article/abstract/220509655?st=search
[10]	晁武杰, 唐志军, 林国栋, 等. 基于桥臂电抗器耦合的MMC-HVDC系统故障过流抑制方法[J]. 电测与仪表, 2023, 60(12): 111-116. CHAO Wujie, TANG Zhijun, LIN Guodong, et al. Fault over-current suppression method for MMC-HVDC system based on bridge arm reactor coupling[J]. Electrical Measurement & Instrumentation, 2023, 60(12): 111-116.
[11]	俞永杰, 吕煜, 邓伟成, 等. 采用架空线等效模型的直流电网故障电流计算方法及实验验证[J]. 中国电机工程学报, 2020, 40(23): 7530-7538. YU Yongjie, LÜ Yu, DENG Weicheng, et al. Fault current calculation method in complex frequency domain of MMC-HVDC grid using equivalent model of transmission line[J]. Proceedings of the CSEE, 2020, 40(23): 7530-7538.
[12]	张孝荟, 汤亚芳, 袁旭峰, 等. 一种混合式直流故障限流器的设计与仿真[J]. 南方电网技术, 2022, 16(2): 74-81. ZHANG Xiaohui, TANG Yafang, YUAN Xufeng, et al. Design and simulation of a hybrid DC fault current limiter[J]. Southern Power System Technology, 2022, 16(2): 74-81.
[13]	赵成勇, 宋冰倩, 许建中. 柔性直流电网故障电流主动控制典型方案综述[J]. 电力系统自动化, 2020, 44(5): 3-13. ZHAO Chengyong, SONG Bingqian, XU Jianzhong. Overview on typical schemes for active control of fault current in flexible DC grid[J]. Automation of Electric Power Systems, 2020, 44(5): 3-13.
[14]	周猛, 向往, 左文平, 等. 柔性直流电网主动限流开断直流故障研究[J]. 中国电机工程学报, 2019, 39(23): 6852-6866. ZHOU Meng, XIANG Wang, ZUO Wenping, et al. Research on DC fault isolation of MMC based DC grid using the active current-limiting approach[J]. Proceedings of the CSEE, 2019, 39(23): 6852-6866.
[15]	陈磊, 何慧雯, 王磊, 等. 基于半桥型MMC的柔性直流电网故障限流方法综述[J]. 电力系统保护与控制, 2021, 49(21): 175-186. CHEN Lei, HE Huiwen, WANG Lei, et al. Review of the fault current limiting approaches for a flexible DC grid based on a half-bridge MMC[J]. Power System Protection and Control, 2021, 49(21): 175-186.
[16]	郝晓弘, 黄伟, 裴婷婷, 等. 一种新型直流故障限流器拓扑[J]. 自动化与仪表, 2021, 36(11): 1-5, 10. HAO Xiaohong, HUANG Wei, PEI Tingting, et al. A novel DC fault current limiter topology[J]. Automation & Instrumentation, 2021, 36(11): 1-5, 10.
[17]	郝晓弘, 黄伟, 裴婷婷, 等. 基于模块化多电平换流器的高压直流系统直流侧故障限流技术研究[J]. 全球能源互联网, 2022, 5(1): 23-34. PEI Tingting, HUANG Wei, PEI Tingting, et al. Research on current limiting technology of DC-side fault of high voltage direct current system based on modular multilevel converter[J]. Journal of Global Energy Interconnection, 2022, 5(1): 23-34.
[18]	韩乃峥, 贾秀芳, 赵西贝, 等. 一种新型混合式直流故障限流器拓扑[J]. 中国电机工程学报, 2019, 39(6): 1647-1658. HAN Naizheng, JIA Xiufang, ZHAO Xibei, et al. A novel hybrid DC fault current limiter topology[J]. Proceedings of the CSEE, 2019, 39(6): 1647-1658.
[19]	董鹤楠, 李炳坤, 孙峰, 等. 一种限流型混合直流断路器拓扑[J]. 哈尔滨理工大学学报, 2023, 28(2): 85-91. DONG Henan, LI Bingkun, SUN Feng, et al. A topology of current-limiting hybrid DC circuit breaker[J]. Journal of Harbin University of Science and Technology, 2023, 28(2): 85-91.
[20]	樊强, 赵西贝, 赵成勇, 等. 模块化多电平换流器自适应故障限流控制策略[J]. 电力系统自动化, 2021, 45(17): 126-133. FAN Qiang, ZHAO Xibei, ZHAO Chengyong, et al. Adaptivefault current limiting control strategy of modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17): 126-133.
[21]	李国庆, 杨勇, 辛业春, 等. 基于桥臂电压控制的MMC直流短路主动限流方法[J]. 电网技术, 2021, 45(1): 144-152. LI Guoqing, YANG Yong, XIN Yechun, et al. Active current-limiting method of MMC to handle DC short-circuit based on bridge arm voltage control[J]. Power System Technology, 2021, 45(1): 144-152.
[22]	LACERDA V A, MONARO R M, PEÑA-ALZOLA R, et al. Control-based fault current limiter for modular multilevel voltage-source converters[J]. International Journal of Electrical Power & Energy Systems, 2020, 118: 105750.
[23]	魏兴杰, 张英敏, 刘坤, 等. 半桥型MMC直流侧故障限流组合控制策略[J]. 电力工程技术, 2023, 42(1): 209-217. https://www.epet-info.com/dlgcjs/article/abstract/211123796?st=search WEI Xingjie, ZHANG Yingmin, LIU Kun, et al. Combined control strategy of half-bridge MMC DC side fault current limiting[J]. Electric Power Engineering Technology, 2023, 42(1): 209-217. https://www.epet-info.com/dlgcjs/article/abstract/211123796?st=search
[24]	肖磊石, 卢启付, 冉旺, 等. 直流故障下MMC-HVDC的两段式限流保护策略[J]. 广东电力, 2023, 36(5): 58-66. XIAO Leishi, LU Qifu, RAN Wang, et al. Two-stage current limiting protection strategy for MMC-HVDC under DC fault[J]. Guangdong Electric Power, 2023, 36(5): 58-66.
[25]	倪斌业, 向往, 周猛, 等. 半桥MMC型柔性直流电网自适应限流控制研究[J]. 中国电机工程学报, 2020, 40(17): 5609-5619. NI Binye, XIANG Wang, ZHOU Meng, et al. Research on adaptive-current-limiting control of VSC-HVDC grid based on half-bridge MMC[J]. Proceedings of the CSEE, 2020, 40(17): 5609-5619.
[26]	金恩淑, 杨筱凡, 于新, 等. MMC-HVDC直流侧极间短路暂态特性分析[J]. 电测与仪表, 2020, 57(23): 30-37. JIN Enshu, YANG Xiaofan, YU Xin, et al. Analysis of DC side pole to pole fault transient characteristic in MMC-HVDC[J]. Electrical Measurement & Instrumentation, 2020, 57(23): 30-37.
[27]	王渝红, 傅云涛, 曾琦, 等. 柔性直流电网故障保护关键技术研究综述[J]. 高电压技术, 2019, 45(8): 2362-2374. WANG Yuhong, FU Yuntao, ZENG Qi, et al. Review on key techniques for fault protection of flexible DC grids[J]. High Voltage Engineering, 2019, 45(8): 2362-2374.
[28]	魏晓光, 周万迪, 张升, 等. 模块化混合式高压直流断路器研究与应用[J]. 中国电机工程学报, 2020, 40(6): 2038-2046. WEI Xiaoguang, ZHOU Wandi, ZHANG Sheng, et al. Research and application of modular hybrid high voltage DC circuit breaker[J]. Proceedings of the CSEE, 2020, 40(6): 2038-2046.